Конечные автоматы Finite State Machines

1.

Конечные автоматы
Finite State Machines

2.

Конечный автомат
Понятие «конечный автомат» обозначает
регулярную, стандартную структуру,
позволяющую описывать и синтезировать
последовательностные схемы в обобщенном
виде.
Все синхронные схемы, рассмотренные нами
до сих пор, могут быть представлены в виде
следующей обобщенной структуры.
2

3.

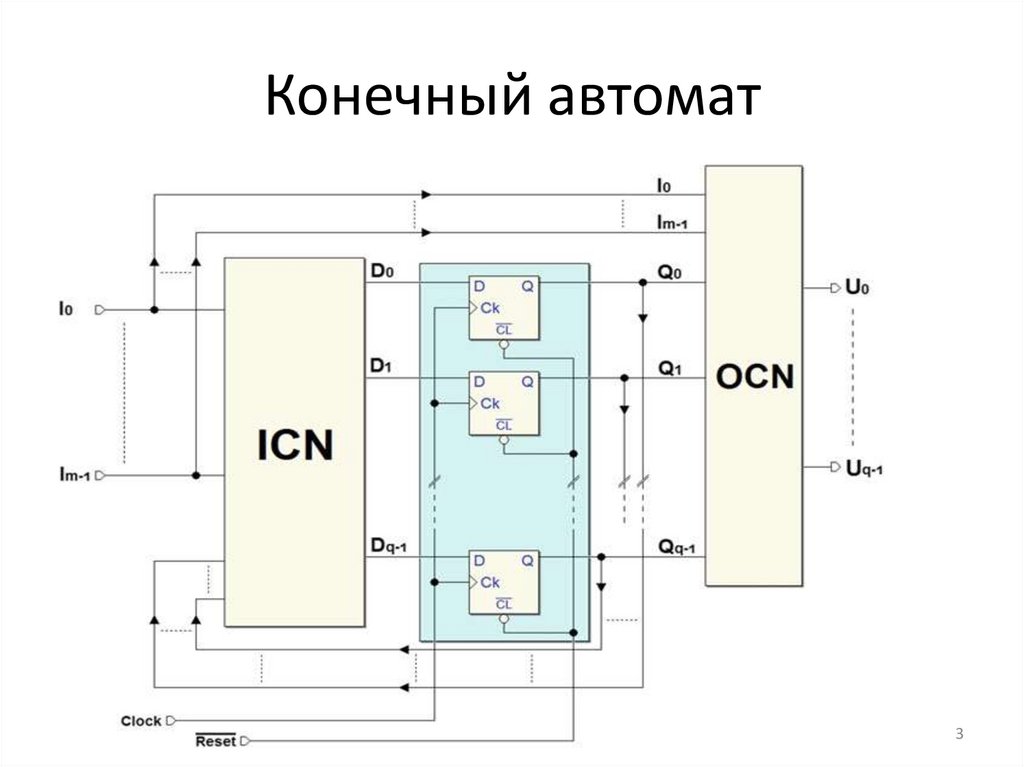
Конечный автомат
3

4.

Стандартная модель
Мы называем состоянием множество значений
зафиксированных триггерами, которые мы
группируем в параллельный регистр или регистр
состояния схемы (выделенный в центре
рисунка).
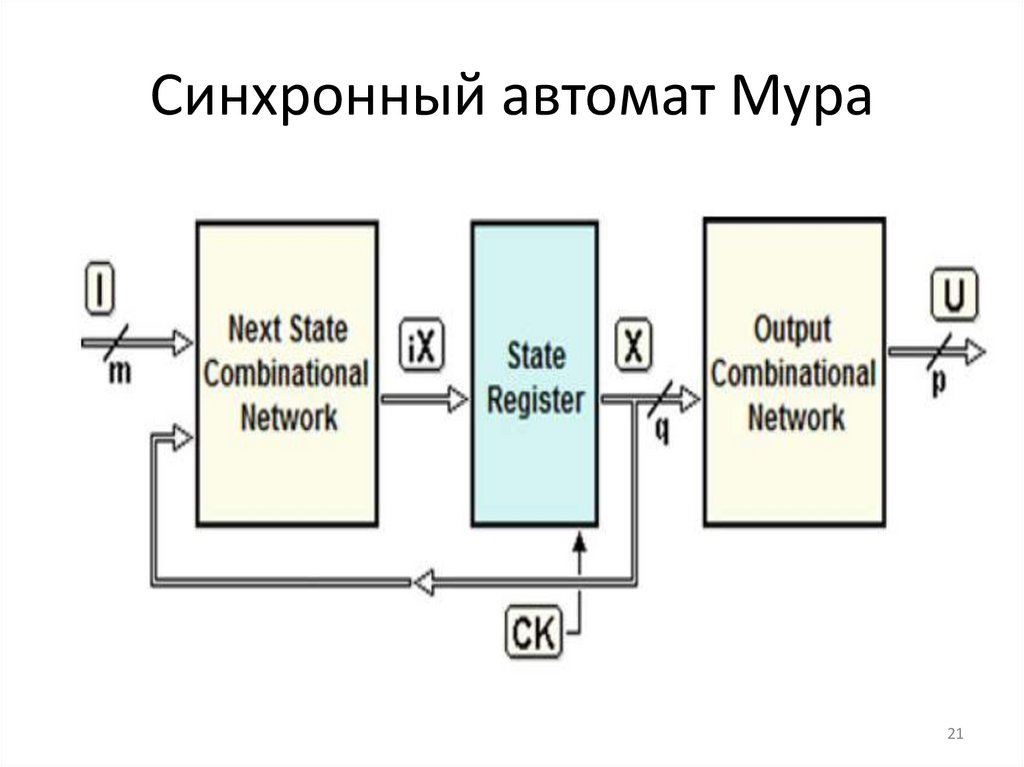
Представляемая стандартная модель пригодна
для описания как синхронных, так и
асинхронных последовательностных схем. В
общем виде последовательностная схема может
быть представлена в виде трех блоков, как
показано на рисунке.
4

5.

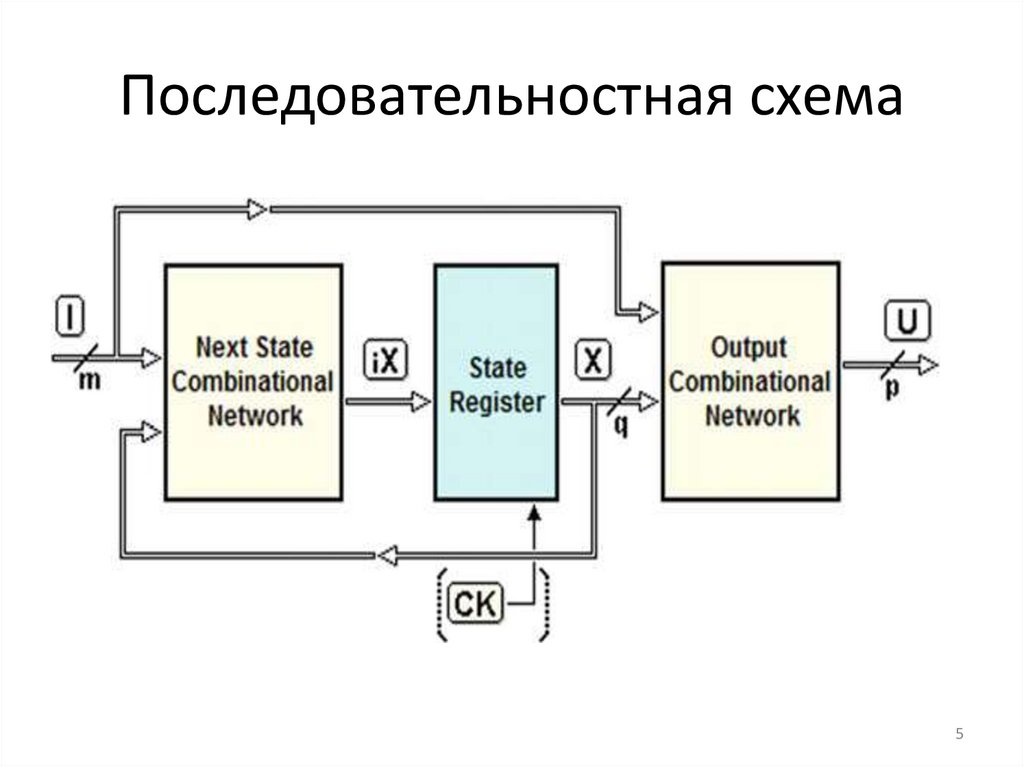
Последовательностная схема
5

6.

Множества переменных
Пусть I, X и U обозначают множества входных
переменных, переменных состояния и
выходных переменных. Множество
переменных называется вектором.
Например, I={I0, I1, I2,…, Im-1}, где m
количество входных переменных. На рисунке
линии, несущие переменные I, X и
U,помечены наклонной чертой с
обозначением количества линий в группе.
6

7.

Вектор состояния X
Средний блок представляет регистр
состояния, в котором хранится вектор
состояния X, определенный множеством q
переменных состояния {X0, X1, X2,…, Xq-1}.
Каждая из 2q комбинаций переменных
определяет некоторое состояние схемы.
Тактовый генератор CK показан в скобках,
потому что он присутствует только в
синхронных схемах.
7

8.

Комбинационная схема следующего
состояния
Комбинационная схема следующего состояния (Next
State Combinational Network), обозначенная на
предыдущем рисунке как ICN, получает вектор входов
I и состояний X и, основываясь на этой информации,
создает вектор iX, который подается на вход регистра
состояния. Как мы видели, вектор X примет значение
вектора iX спустя некоторое время.
Комбинационная схема выхода (Output Combinational
Network) имеет на входе вектор состояний X и вектор
входов I и создает вектор выходов схемы U={U0, U1,
U2, … Up-1}.
8

9.

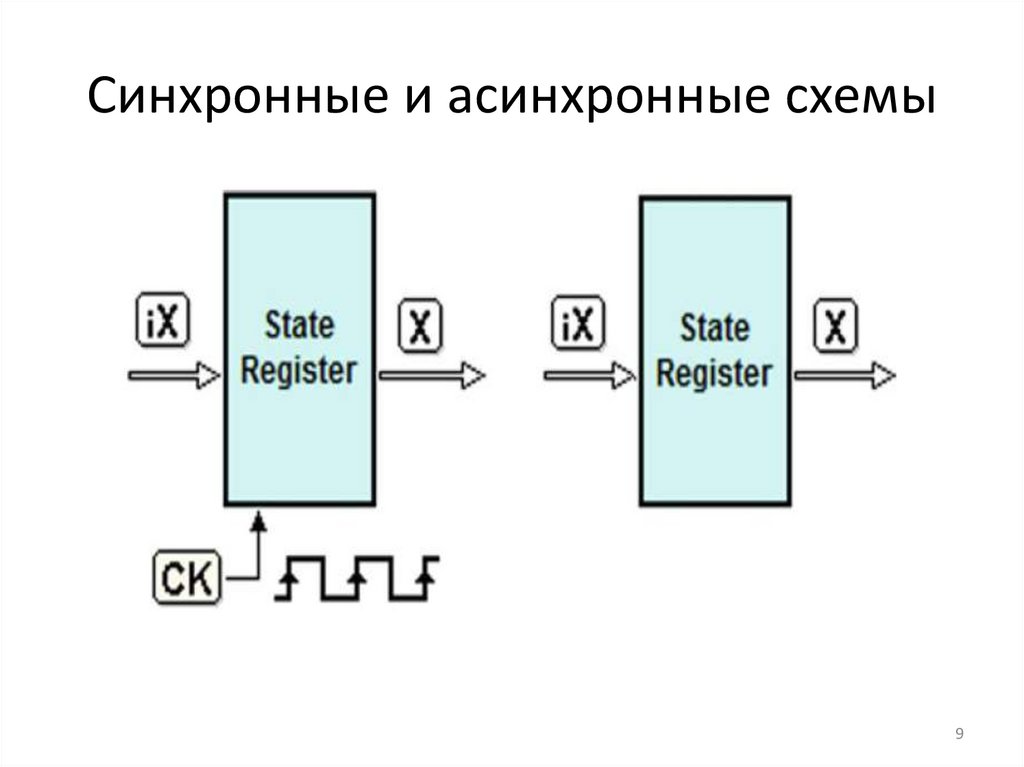
Синхронные и асинхронные схемы
9

10.

Синхронные и асинхронные схемы
Временная эволюция схемы определяется структурой
регистра состояния. Если регистр состояния включает
тактируемые триггеры, тактируемые одним
генератором, то последовательностная схема
описывается моделью синхронного конечного
автомата.
Если же регистр состояния использует асинхронные
триггеры, схема описывается моделью асинхронного
автомата. При этом временная эволюция схемы
определяется изменениями на входах и внутренними
задержками схемы.
10

11.

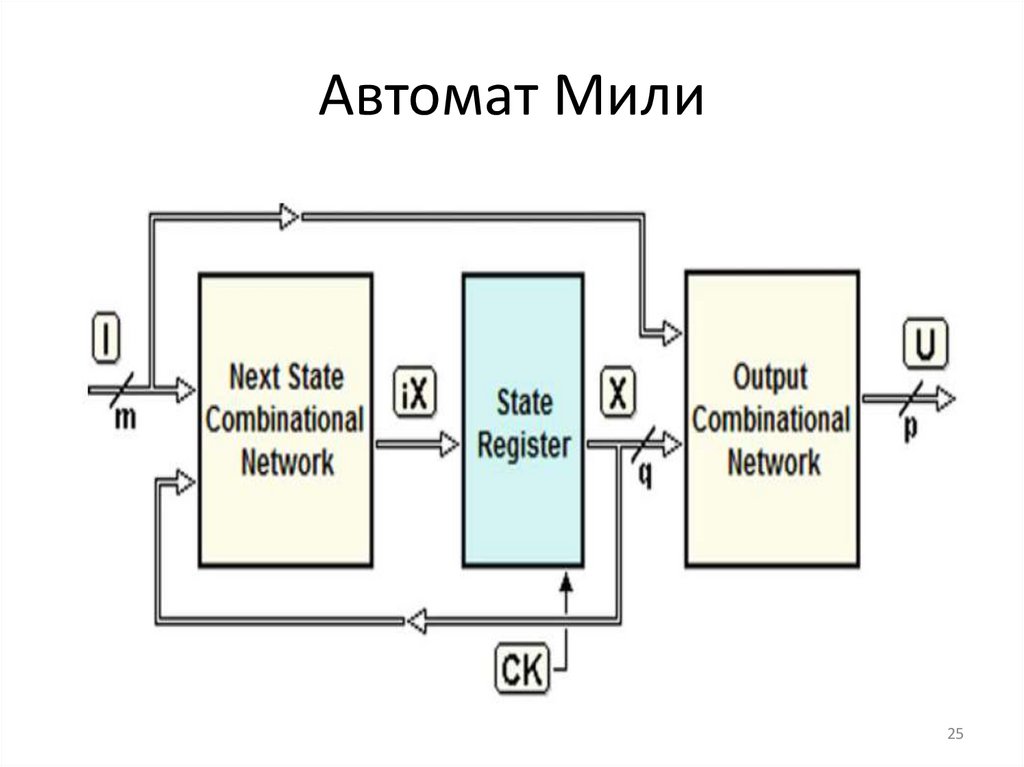
Автоматы Мура и Мили
Имеется два варианта получения выходных
значений. Стандартная модель, где выходные
значения являются функциями состояния и
входных значений обычно называется
автоматом Мили. В автомате Мура выходы
являются функциями только состояния.
11

12.

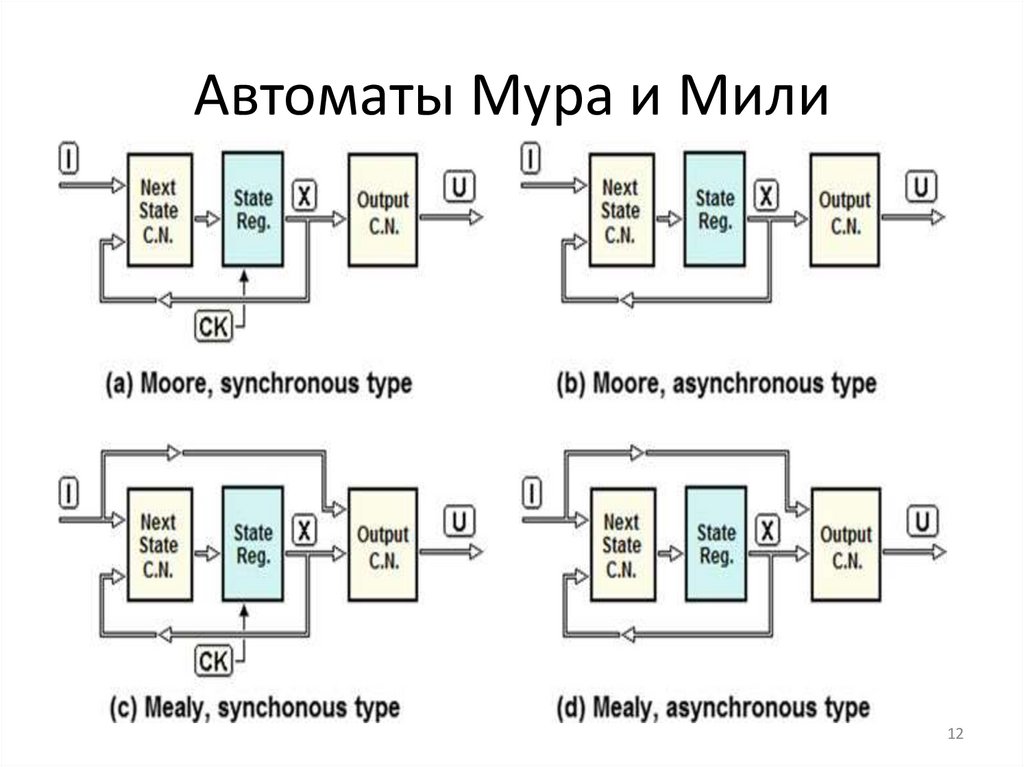
Автоматы Мура и Мили
12

13.

Автоматы Мура и Мили
Модели слева (a) и (c) являются
синхронными. Синхронизация с помощью
тактового генератора обеспечивает
изменение состояний на активных фронтах
тактовых импульсов. Модели справа (b) и (d)
являются асинхронными. В автоматах Мура
(a) и (b) нет связи между входами и
комбинационной схемой для выхода.
Напротив, в автоматах Мили (c) и (d) она
имеется.
13

14.

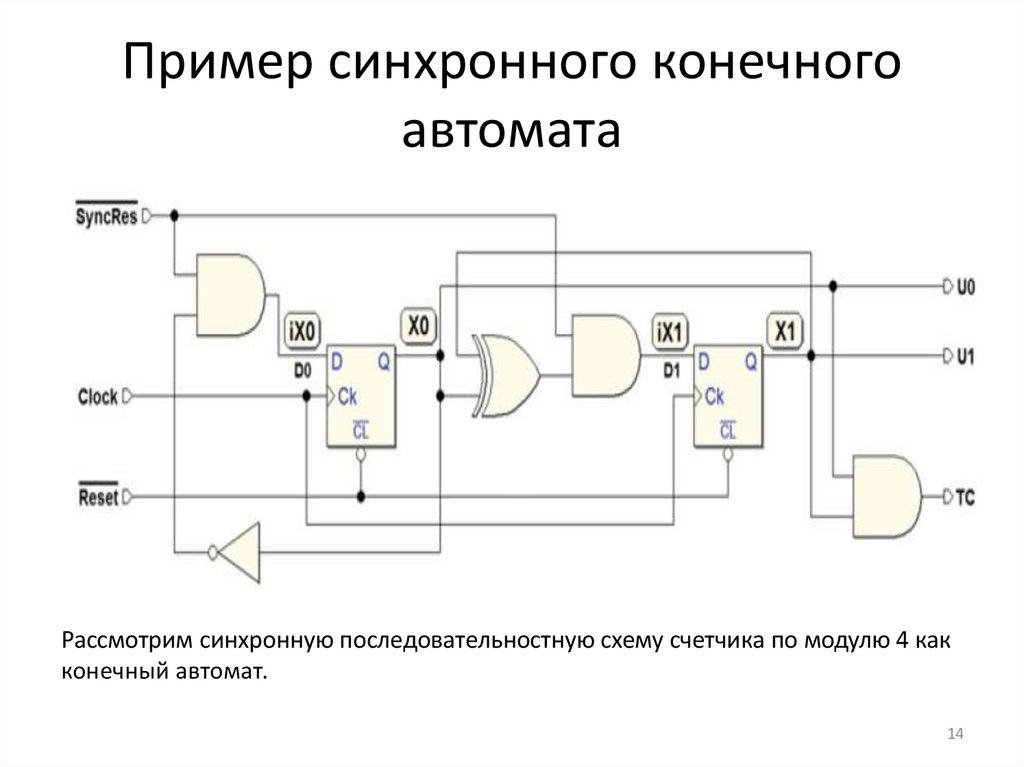
Пример синхронного конечного
автомата
Рассмотрим синхронную последовательностную схему счетчика по модулю 4 как
конечный автомат.
14

15.

Пример синхронного конечного
автомата
Как видно на рисунке схема использует два
триггера типа D-PET. Они могут
рассматриваться как элементы памяти,
формирующие регистр состояния и их
выходы являются переменными состояния
(X0, X1):
Представление в виде конечного автомата
15

16.

Синхронный автомат Мура
16

17.

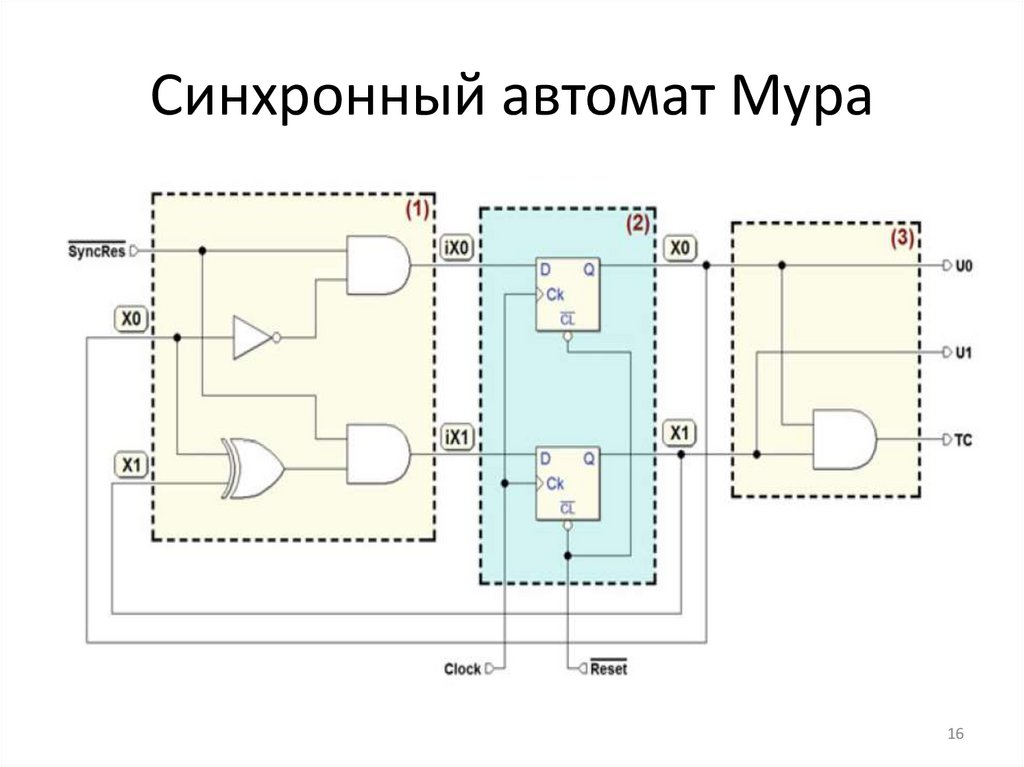
Синхронный автомат Мура
На рисунке мы видим набор логических
вентилей, которые вычисляют значения на
входах вентилей D, как функции от внешнего
входа