Similar presentations:
Скалярное произведение векторов. Вычисление углов между прямыми
1.
Скалярное произведениевекторов.
Вычисление углов между
прямыми.
2.
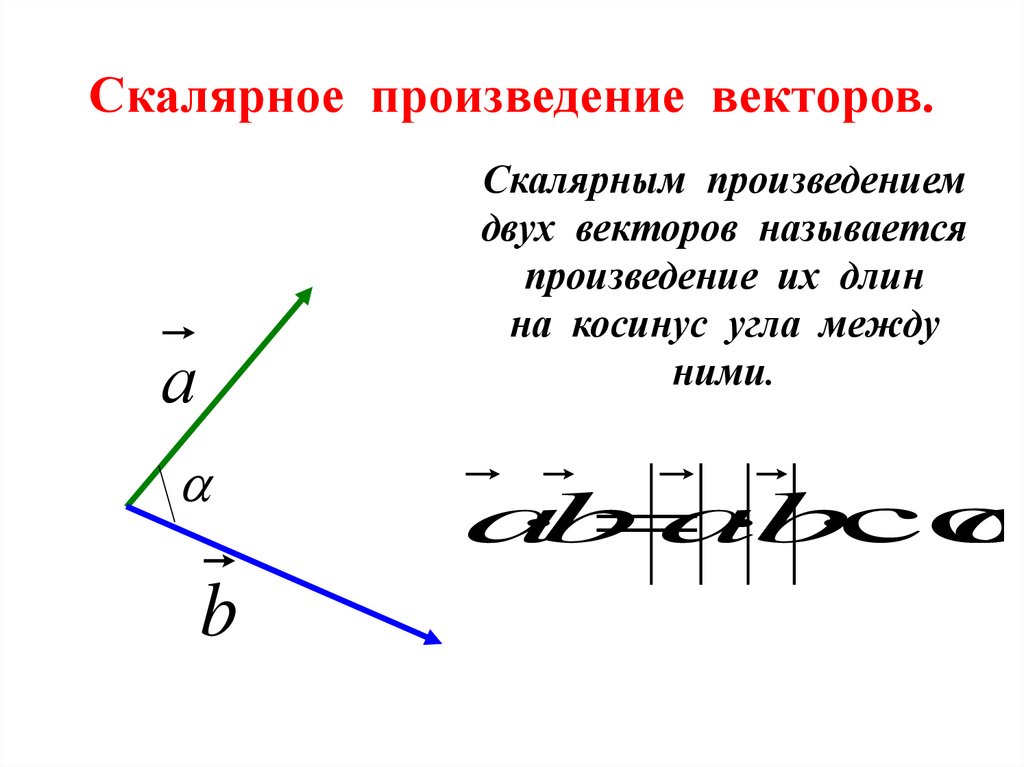
Скалярное произведение векторов.Скалярным произведением
двух векторов называется
произведение их длин
на косинус угла между
ними.
а
b
a
b
a
b
cos
3.
ab a b cos
Если
Если
Если
a b = 0
a b 0
, то
a b
- острый угол
a b 0 , то - тупой угол
, то
4.
Формула скалярного произведениявекторов в пространстве.
а x1;y1;z1
b x2;y2;z2
a
b
x
x
y
y
z
z
1
2
1
2
1
2
Скалярное произведение двух векторов равно
сумме произведений соответствующих
координат этих векторов.
5.
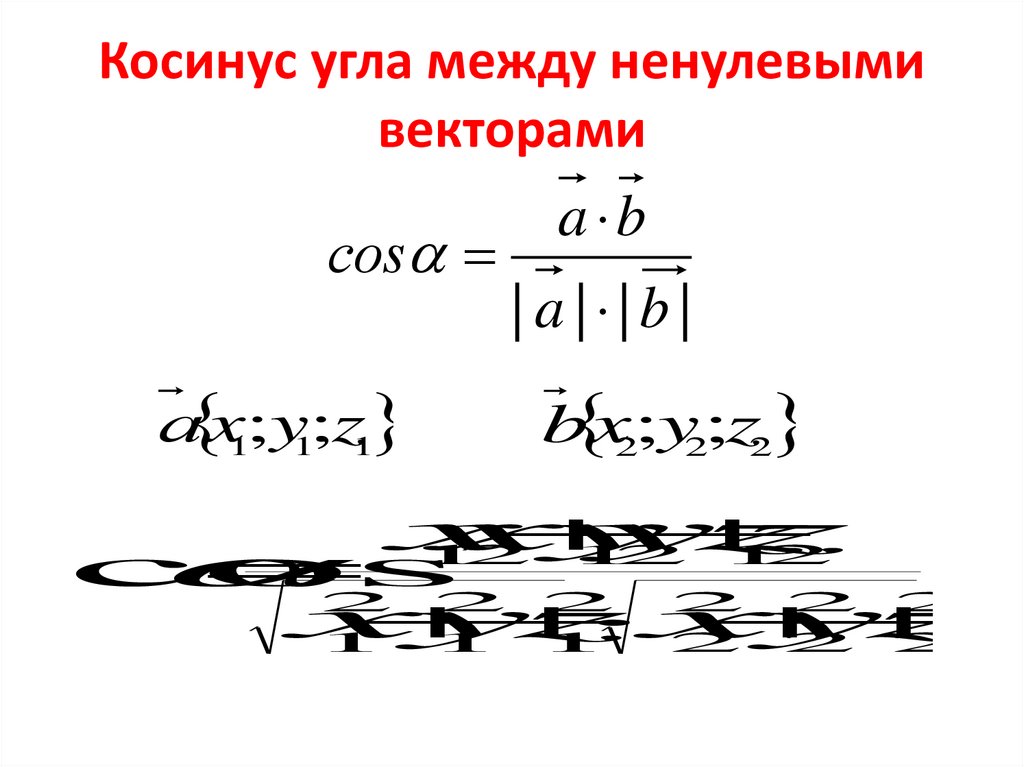
Косинус угла между ненулевымивекторами
соs
а x1;y1;z1
a b
| a | |b |
b x2;y2;z2
x
x
y
y
z
z
1
2
1
2
1
2
cos
2 2 2
2 2 2
x
y
z
x
y
z
1
1
1
2
2
2
6.
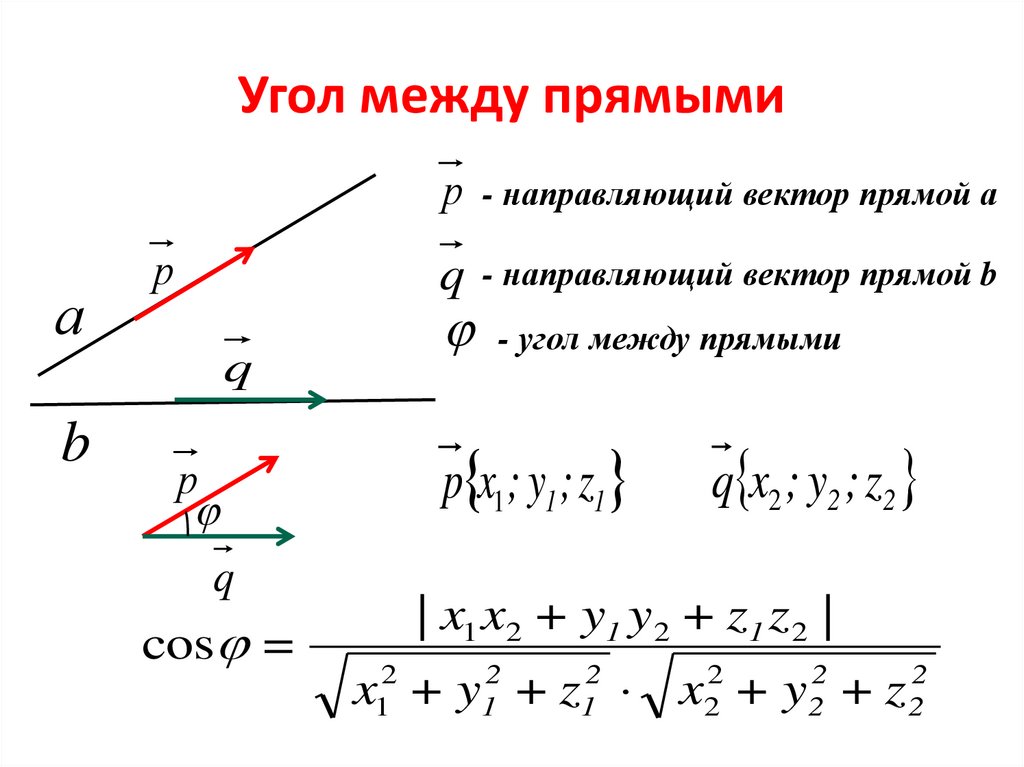
Угол между прямымир - направляющий вектор прямой а
а
р
q - направляющий вектор прямой b
- угол между прямыми
q
b
p x1 ; y1 ; z1
р
q
cos =
q x2 ; y2 ; z2
| x1 x2 + y1 y2 + z1 z 2 |
x +y +z x +y +z
2
1
2
1
2
1
2
2
2
2
2
2
7.
№1Вычислить угол между прямыми AB и CD, если
A(5;-8;-1), В(6;-8;-2), С(7;-5;-11), D(7;-7;-9)
Решение
AB 1;0; 1
cos =
СD 0; 2;2
| 1 0 0 ( 2) ( 1) 2 |
12 0 2 ( 1) 2 0 2 ( 2) 2 2 2
1
cos
2
60
0
8.
№2 (Решите самостоятельно)Вычислить угол между прямыми AB и CD, если
A(1;0;2), В(2;1;0), С(0;-2;-4), D(-2;-4;0)
9.
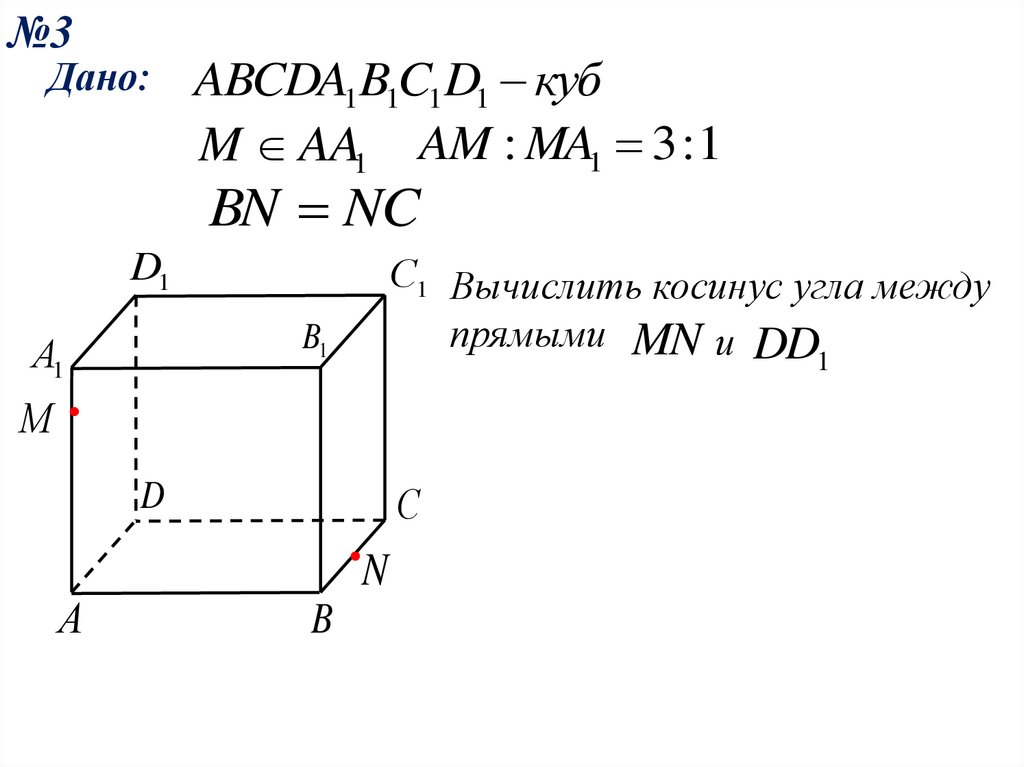
№3Дано:
ABCDA1B1C1D1 куб
M AA1 AM : MA1 3 : 1
BN NC
С1 Вычислить косинус угла между
D1
прямыми MN и DD
B1
А1
1
М
С
D
А
N
B
10.
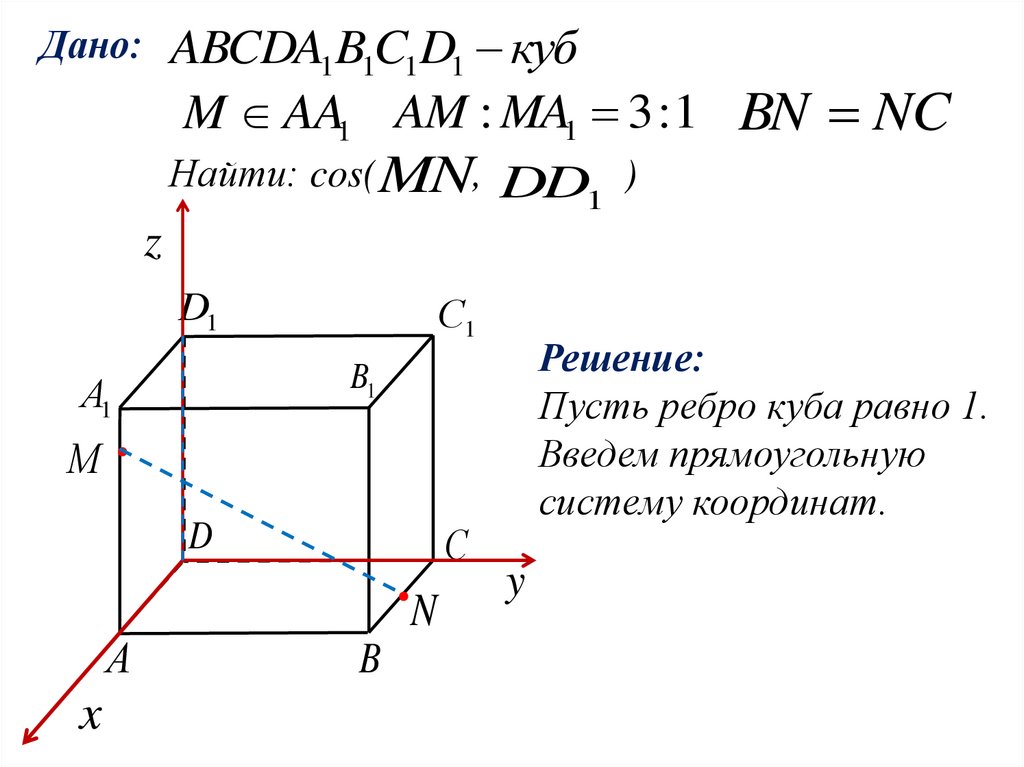
Дано: ABCDA1B1C1D1 кубM AA1 AM : MA1 3 : 1 BN NC
Найти: cos( MN, DD )
1
z
С1
D1
Решение:
Пусть ребро куба равно 1.
Введем прямоугольную
систему координат.
B1
А1
М
С
D
А
x
N
B
y
11.
zС1
D1
B1
А1
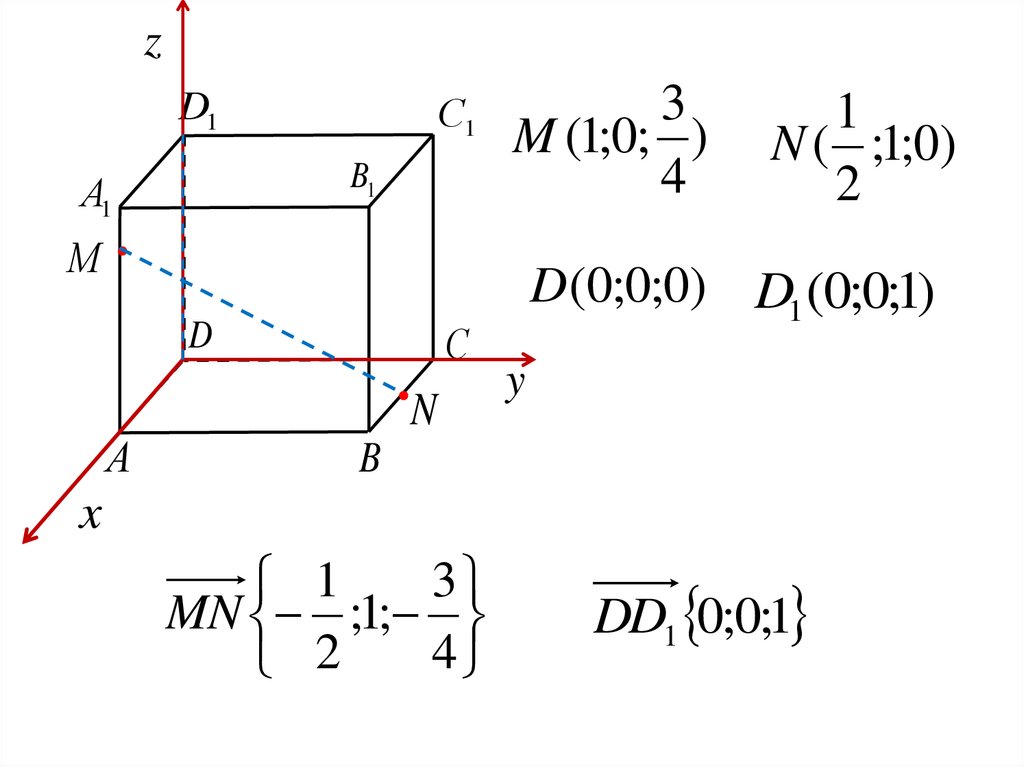
3
M (1;0; )
4
М
С
D
А
N
1
N ( ;1;0)
2
D (0;0;0) D1 (0;0;1)
y
B
x
3
1
MN ;1;
4
2
DD1 0;0;1
12.
31
MN ;1;
4
2
cos =
DD1 0;0;1
1
3
| 0 1 0 ( ) 1 |
2
4
2
2
1
3
2
2
2
2
1 0 0 1
2
4
3
cos
29
13.
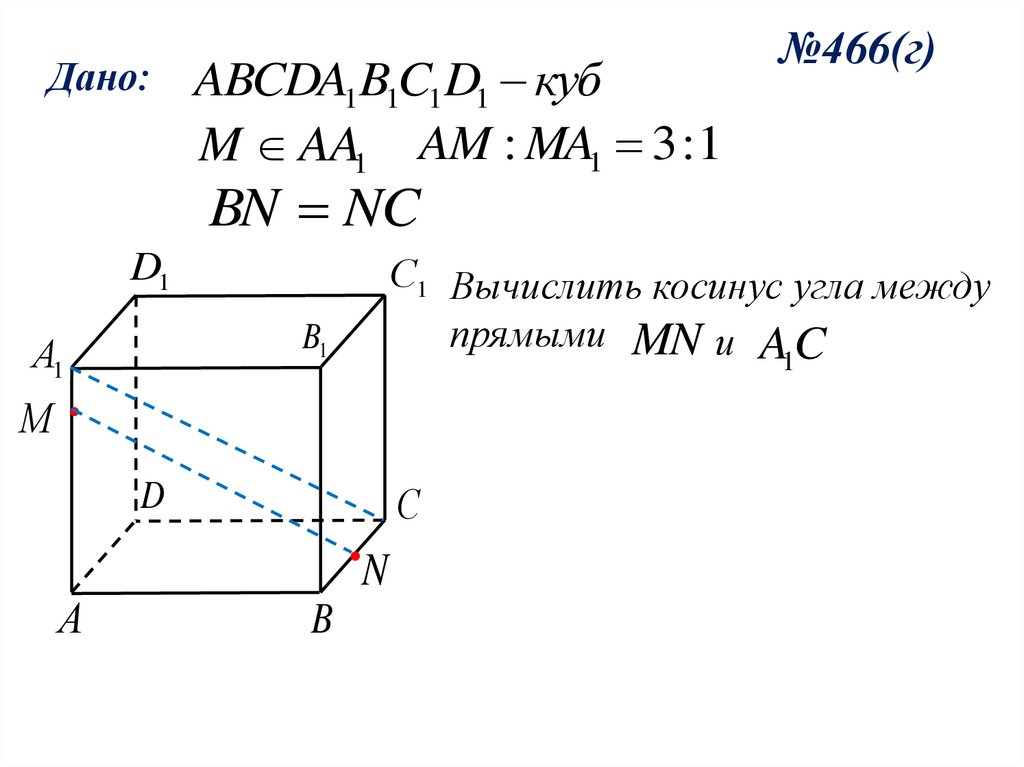
Дано:ABCDA1B1C1D1 куб
M AA1 AM : MA1 3 : 1
№466(г)
BN NC
С1 Вычислить косинус угла между
D1
прямыми MN и A C
B1
А1
1
М
С
D
А
N
B

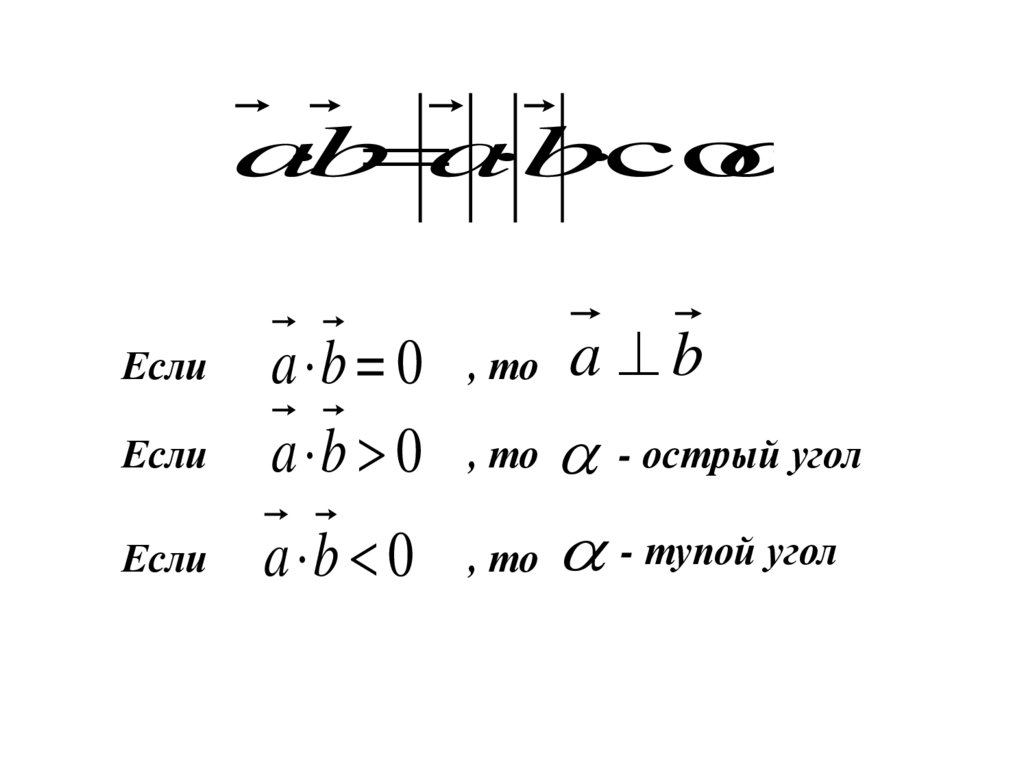



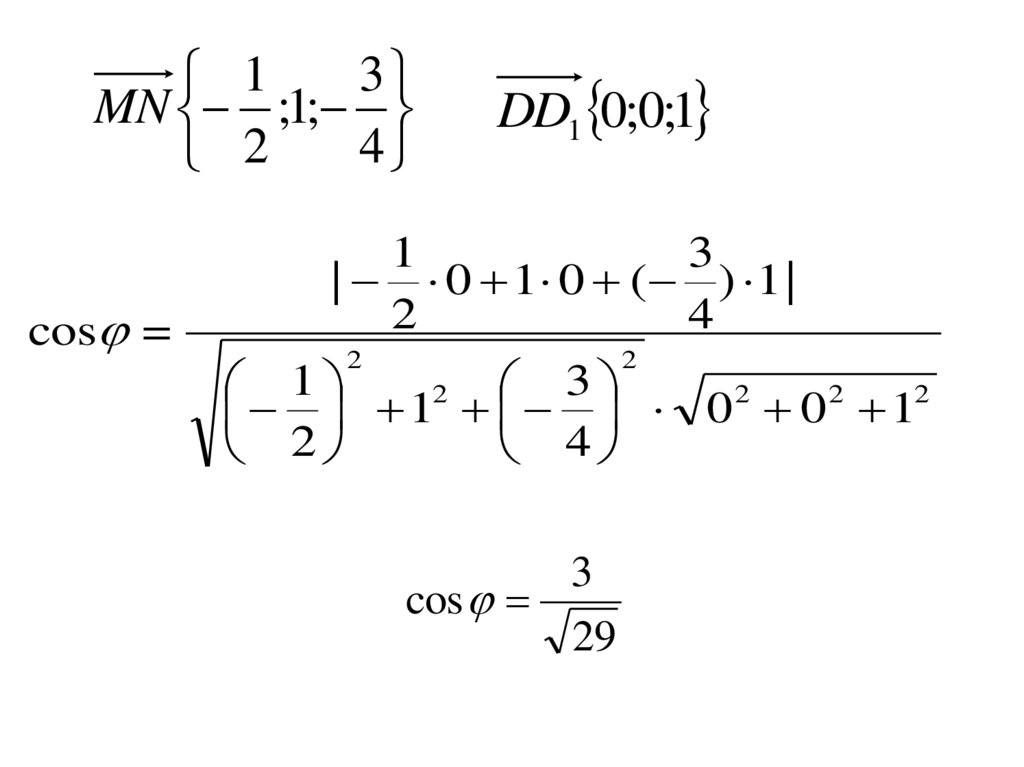
 mathematics
mathematics








