Similar presentations:
Системы счисления. Урок 10.1
1.
Системы счисления2.
Системы счисления (СС)– это правила, позволяющие записывать различныечисла с помощью цифр или же различных символов.
Существует два основных вида СС:
непозиционные
ХХХ = 10+10+10=30
- на какой бы позиции не располагался
символ «X», он определяет значение
равное 10
позиционные
333 = 3*100+3*10+3*1 – символ «3» в зависимости от позиции
в числе определяет разное значение:
300, 30 или 3.
3.
Непозиционные СС. Римская ССI=1
V=5
X = 10
L = 50
С = 100
D = 500
M = 1000
Правила записи чисел:
1) Число как говорится, так и пишется.
2) Если цифра слева меньше, чем цифра справа, из большей
цифры вычитаем меньшую
IV
: 1 < 5, поэтому, 5 – 1 = 4
XL
: 10 < 50, поэтому, 50 – 10 = 40
3) если цифра справа меньше или равна цифре слева, цифры
складываем
VI
: 5+1=6
VIII : 5 + 1 + 1 + 1 = 8
XX
: 10 + 10 = 20
4) Не может идти подряд четыре одинаковых знака (или перед
большей может стоять только одна меньшая).
4.
I=1V=5
X = 10
L = 50
С = 100
D = 500
M = 1000
Примеры:
III =3
VI =6
XII=12
XXVIII = 28
ХХХIХ = 39
CCCXCVII = 397
MDCCCXVIII = 1818
MCMLXIV = 1964
5.
Позиционные ССОснование СС (ОСС) – количество используемых для записи чисел
знаков.
• Десятеричная – 0,1,2,3,4,5,6,7,8,9
• Пятеричная – 0,1,2,3,4
• Троичная – 0,1,2
• Двоичная – 0,1
• Двенадцатеричная – 0,1,2,3,4,5,6,7,8,9,А,В
• Шестнадцатеричная – 0,1,2,3,4,5,6,7,8,9,А,В,С,D,E,F
Максимальная цифра на 1 меньше основания СС
6.
Принцип построения10-ричная:
Например: 7286
базис десятичной системы счисления
7.
Принцип построения5-ричная:
Например:
3241
базис пятеричной системы счисления
8.
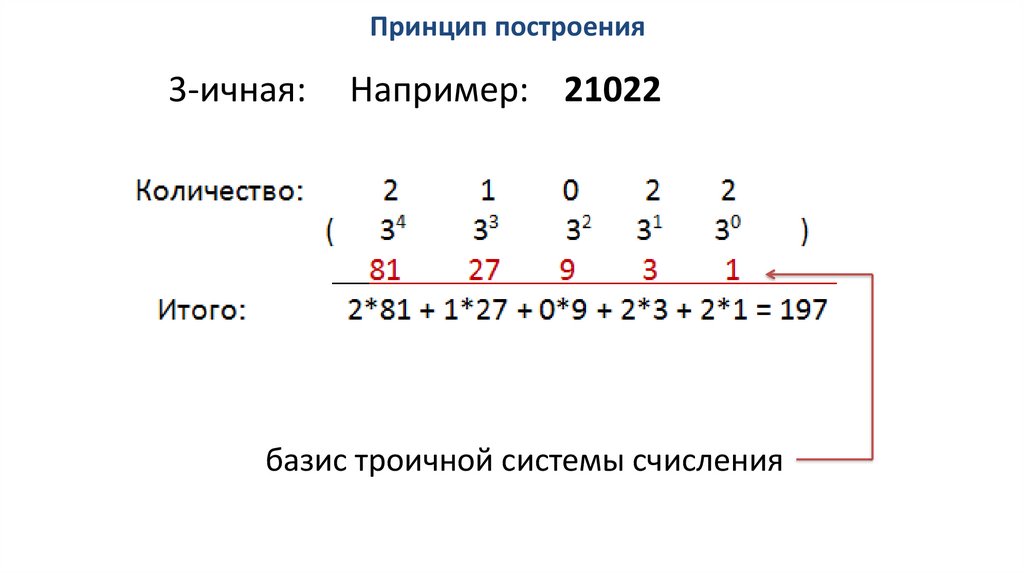
Принцип построения3-ичная:
Например: 21022
базис троичной системы счисления
9.
Принцип построения2-ичная:
Например: 11011
базис двоичной системы счисления
10.
Принцип построения16-ричная:
Например: 1А8F
базис шестнадцатеричной системы счисления
11.
Алгоритм (правило) перевода из любой СС в десятичную(Ар → Х10)
1. Двигаемся справа-налево;
2. Под первой цифрой подписываем 1, а под каждой
следующей число, равное предыдущему, умноженному
на ОСС (- это базис СС);
3. Умножаем верхние цифры на нижние числа;
4. Складываем полученные результаты.
12.
Задание 1. Написать числа, стоящие непосредственнопред и после написанного:
1) 4999
500010
5001
2) …
4445
…
3) …
199912
…
4) …
1A9D14
…
5) …
1000112
…
13.
Задание 2.Перевести:
1) 2879 = X10
2) 77716 = X10
3) 101105 = X10
4) 100100102 = Х10
Решение пункта 4:
Кол-во:
Итого
1
128
0
0
64
+ 32
1
16
0
0 1
8 +4
2
0
1
= 146
14.
Алгоритм (правило) перевода из десятичной СС в любую(А10 → Хр)
Метод деления.
1. Делим нацело исходное число на ОСС и получаем частное и
остаток.
2. Если частное больше или равно ОСС, то частное – это новое
исходное число и повторяем пункт 1.
Если частное меньше ОСС, то выписываем последнее
частное и остатки в обратном порядке, не забывая, что если
переводим в СС > 10, то остатки большие 9 нужно заменить
на соответствующую букву.
15.
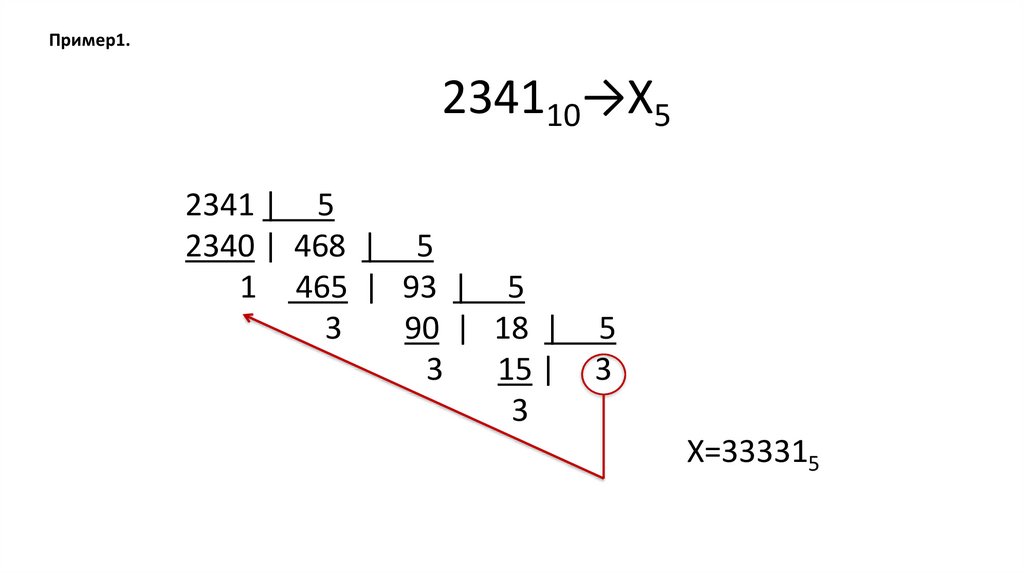
Пример1.Пример1.
234110→Х5
2341 | 5
2340 | 468 | 5
1 465 | 93 | 5
3
90 | 18 |
3
15 |
3
5
3
X=333315
16.
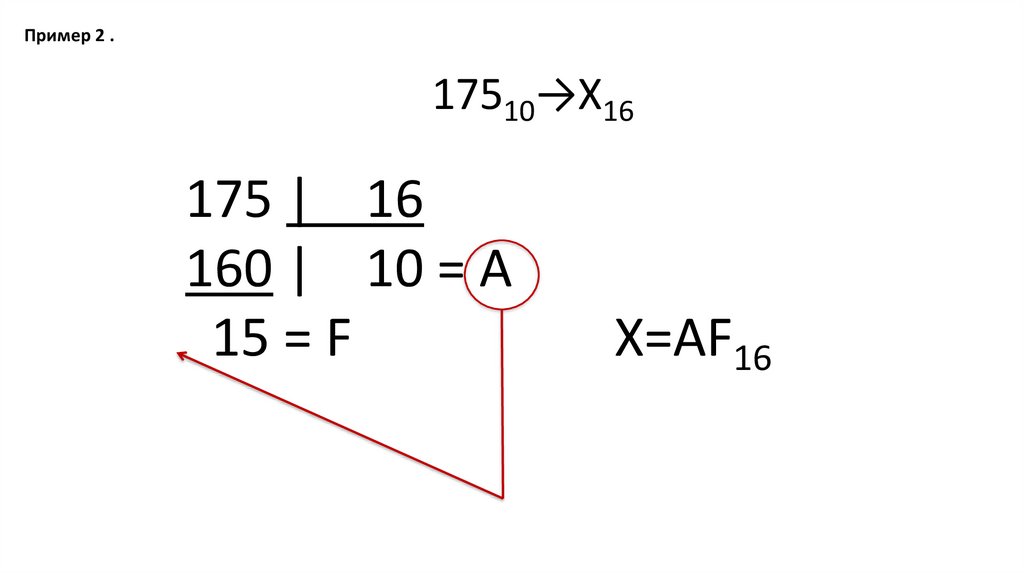
Пример 2 .Пример 2 .
17510→Х16
175 | 16
160 | 10 = A
15 = F
X=AF16
17.
Задание 3.Перевести (методом деления) :
1101010 = X12
18.
Алгоритм (правило) перевода из десятичной СС в любую (А10 → Хр)Метод вычитания
1. Выписываем справа налево базис системы счисления в которую
переводим исходное число до тех пор пока очередные числа базиса
меньше исходного числа.
2. Смотрим, сколько раз очередное максимальное число базиса
укладывается в исходном числе, подставляем это число под
максимальным числом базиса, умножаем его на максимальное число
базиса и вычитаем из исходного числа.
3. Повторяем п.2 до тех пор, пока разность не станет равна 0.
4. Незаполненные промежутки под базисными числами заполняем нулями.
Это и есть полученный результат.
19.
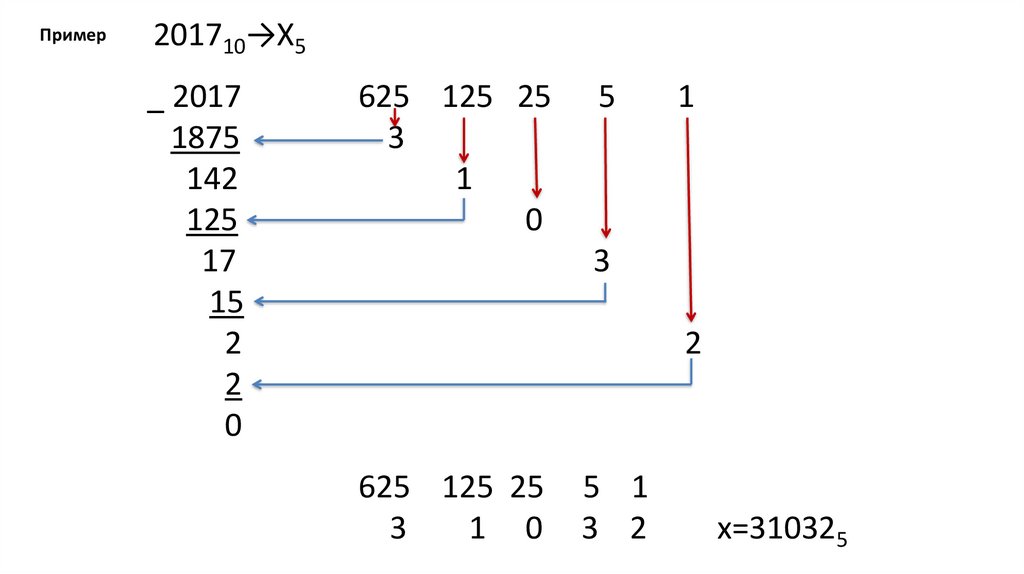
Пример201710→Х5
_ 2017
1875
142
125
17
15
2
2
0
625 125 25
3
1
0
5
1
3
2
625 125 25
3
1 0
5 1
3 2
х=310325
20.
Задание 4.Перевести (методом вычитания):
1) 1101010=X14
2) 19010 = Х2
21.
Арифметика в СССложение
1. Складываем в 10 СС все цифры чисел, начиная с младших, учитывая и
возможный перенос из предыдущего разряда.
2. Смотрим, сколько раз ОСС укладывается в полученном числе и каков
остаток. Остаток записываем в результат (не забывая, что в случае
вычисления в СС>10 и получения остатка>10, его нужно заменить на
соответствующую букву), а количество укладывающихся ОСС пойдет
переносом в следующий разряд.
3. Выполняем п.1, п.2 для всех разрядов.
22.
Пример:X=5AFFF16 + ABCDEF16+ 678916+ 1234516
5 A F F F16
A B C D E F16
6 7 8 916
1 2 3 4 516
B308BC
X= B308BC16
0(перенос)+ F(15)+F(15)+9+5= 44 = 16 * 2 + 12(C)
2(перенос)+ F(15)+E(14)+8+4= 43 = 16 * 2 + 11(B)
2(перенос)+ F(15)+D(13)+7+3= 40 = 16 * 2 + 8
2(перенос)+ A(10)+C(12)+6+2= 32 = 16 * 2 + 0
2(перенос)+ 5+B(11)+1= 19 = 16 * 1 + 3
1(перенос)+ A(10)= 11 = 16 * 0 + 11(B)
23.
Задание 5.Вычислить:
1) 233335+43215+44444445+33335+10203045
2) 1000111012+11101112+101101102+ 110110112+ 11111112
24.
Умножение.Алгоритм аналогичен сложению, но перенос
добавляется к следующему умножению (если
умножение на очередное число не закончено, или к
следующему разряду в противном случае.
25.
УмножениеАлгоритм аналогичен сложению, но перенос добавляется к следующему умножению (если умножение на
очередное число не закончено, или к следующему разряду в противном случае.
Пример:
Х = АВ0512 * А0612
АВ06
B05
46726
A0156
A060 126
6*5=30 = 12*2+6
5*B(11) = 55 = 12*4+7
4+5*A(10) =54 = 12*4+6
B(11)*6=66 = 12*5+6
B(11)*B(11) = 121 = 12*10+1
10+ B(11)* A(10) = 120 = 12*10+0
X=A06012612
26.
Задание 6.Вычислить:
X16 =FC916*AB0616
27.
ВычитаниеВычитаем, как обычно справа налево.
1. Если очередная цифра уменьшаемого больше или равна цифре
вычитаемого, то просто вычитаем одно из другого.
2. Иначе занимаем единицу (если это возможно, то есть он ≠ 0) у
следующего по старшинству разряда. При этом из занимаемой цифры
вычитаем 1, а к младшему разряду прибавляем число, равное
основанию системы счисления.
3. Если у старшего разряда занять не можем (то есть он =0), то занимаем
у следующего по старшинству, который ≠ 0. При этом в более младший
переносим число = ОСС и тогда уже занимаем у него.
28.
Пример.Х5 = 3100215 - 231325
Х = 2313345
29.
Задание 7. Вычислить:1) A09DB00616 - 9AFC75316 = X16
2) 1001011002 - 1110111012 = X2
30.
ДополнениеДополнением называется число, которое нужно
прибавить к исходному, чтобы получилось число,
состоящее из 1 с количеством «0», равным количеству
цифр в исходном числе.
Например в 10СС:
56012 + Д = 100000
откуда
Д = 100000 – 56012
31.
Получение дополнения в любой СС.1. Двигаемся справа-налево.
2. Если число заканчивается нулями, то переносим их в
получаемое дополнение.
3. Первую значащую цифру (не 0) вычитаем из основания СС.
4. Все остальные цифры вычитаем из числа на 1 меньше
основания СС.
Пример: Д(50234008)
5 0 2 3 4 0 08
Д= 2 7 5 4 4 0 0
32.
Получение дополнения в двоичной СС.1. Инвертируем исходное число (то есть меняем 0 на 1 и 1 на 0)
2. К полученному числу прибавляем 1 в младшем разряде.
Пример: Д(11101002)
1 1 1 0 1 0 02
1.
0001011
2. +
1
Д=
1 1 0 02
33.
Вычитание через сложение9203 – 7654 =
9203 + (10000 – 7654) - 10000.
Выражение в скобках – это дополнение вычитаемого, а 10000 –
число, до которого дополняли.
34.
Алгоритм вычитания в любой СС1. Уравниваем количество
незначащие нули.
разрядов,
добавив
слева
2. Получаем дополнение вычитаемого с учетом добавленных
нулей.
3. Складываем уменьшаемое с полученным дополнением.
4. Отбрасываем 1 в старшем разряде.
Примечание: все операции выполняем в заданной СС.
35.
Пример: 9213412 – 715612«Уравниваем» разряды :
9213412 – 0715612
Находим дополнение для вычитаемого:
0 7 1 5 612
Д= В 4 А 6 612
Складываем уменьшаемое и полученное дополнение
9213412
+ В4А6612
186В9А
Отбрасываем единицу в старшем разряде
186В9А = 86В9А12
36.
Задание 8.Вычислите через сложение:
A09DB00616 - 9AFC75316 = X16
37.
Вычитание через сложение в двоичной СС.1. Уравниваем количество разрядов, добавив слева
незначащие нули.
2. К обоим числам слева добавляем по одному нулю (так
называемая подушка безопасности)
3. Получаем дополнение отрицательных чисел с учетом
добавленных нулей.
4. Слева к обоим числам добавляем знак в виде 0, если число
положительное и 1, если отрицательное (это знаковый
разряд)
5.Складываем уменьшаемое с полученным дополнением с
учетом знаковых разрядов (естественно, в двоичной СС).
38.
Вычитание через сложение в двоичной ССПример 1:
Х = 1000100 – 110111
Преобразуем:
х = 1000100 + (-110111)
0110111
01000100 00110111
11001000
+
1
11001001
4. 001000100 111001001
1.
2.
3.
уравниваем разряды
добавляем по нулю к каждому числу
переводим отрицательные
числа в обратный код
добавляемый знаковый разряд
0 – если положительное число
1 – если отрицательное число
39.
5.001000100
+ 111001001
1000001101
6. 10 00001101
7. 0 00001101
складываем числа
зачеркиваем единицу слева
определяем знак числа, в знаковом разряде 0,
значит число положительное, записано в
прямом коде
Ответ: X = 11012
Проверка:
10001002 (4+64=68) – 1101112 (1+2+4+16+32=55) =11012 (1+4+8 = 13)
40.
Пример 2:Х = -11100100 – 10010111
х = - 11100100 + (- 10010111)
1. Количество разрядов одинаково по 8
2. 011100100
010010111
3. 100011011
+
1
100011100
101101000
+
1
101101001
4. 1100011100
1101101001
добавляем по нулю к каждому числу
переводим отрицательные
числа в обратный код
добавляемый знаковый разряд
0 – если положительное число
1 – если отрицательное число
41.
5.1100011100
+ 1101101001
11010000101
6.
7.
11 010000101
1 010000101
складываем
зачеркиваем единицу слева
определяем знак числа, в знаковом разряде 1,
значит число отрицательное, записано в
обратном коде. Переводим в прямой код, находим
дополнение к дополнению
010000101
101111010
+
1
101111011
Ответ: Х = - 101111011
42.
Проверка:-11100100 (4+32+64+128=-228) – 10010111 (1+2+4+16+128=151) =
- 101111011 (1+2+8+16+32+64+256=-379)
Задание 9.
Вычислите через сложение:
1001011002 - 1110111012 = X2
43.
ДелениеЧаще всего деление проводят с точностью до заданного знака
после запятой (конечно, если не получается деления нацело
или периодическая дробь). Рассмотрим на примере деления
двоичных чисел с точностью 5 знаков после запятой.
Пример:
1001010 : 10111 = Х
44.
100101’0 1011110111
11. 00110
11100
10111
101000
10111
100010
10111
10110
X=11.001102
45.
Задание 10.Вычислите с точностью до 4-го знака после запятой:
1001000012 : 1100102 = X2
46.
Родственные системы счисленияДве системы счисления называются родственными, если основание одной
системы счисления равно степени основания другой системы счисления.
Например:
двоичная (21),
четверичная (22),
восьмеричная (23),
шестнадцатеричная (24) …
47.
Алгоритм перевода из 8(16) -ричной в двоичную СС.
Пример: 3602.568 → Х2
3
6
0
2 . 5
68
011 110 000 010 . 101 110
Ответ: Х = 11110000010.101112
1. Каждую цифру заменяем
её трех (четырех)
разрядным двоичным
эквивалентом.
2. Отбрасываем
незначащие разряды.
Задание 11 . Переведите:
1АF00C.2E16 → Х2
48.
Алгоритм перевода из двоичной в 8 (16) -ричную СС1. Двигаемся от запятой в оба направления, отделяя по 3
(4)двоичных разряда.
2. В неоконченные
количество нулей.
группы
добавляем
3. Каждую выделенную группу заменяем
(шестнадцати) –ричным эквивалентом.
недостающее
её
восьми
49.
Пример 1 :11011000001101111.10001112 → Х8
11|011|000|001|101|111 . 100|011|12
011 011 000 001 101 111 . 100 011 1002
3
3
0
1
5
7 . 4
3
4
Ответ: Х8 = 330157.434
Задание 12.
11011000001101111.10001112 → Х16
50.
Задачи для программированияЗадача 1. Вводится трехразрядное целое число в двоичной системе
счисления. Перевести это число в десятеричную СС.
Задача 2. Вводится трехразрядное целое число (а) и основание
системы счисления (q), в которой это число записано. Перевести это
число в десятеричную СС.
Задача 3. (дополнительное задание)
Задается целое двухразрядное число в восьмеричной СС. Перевести
его в
а) двоичную СС
б) шестнадцатеричную СС























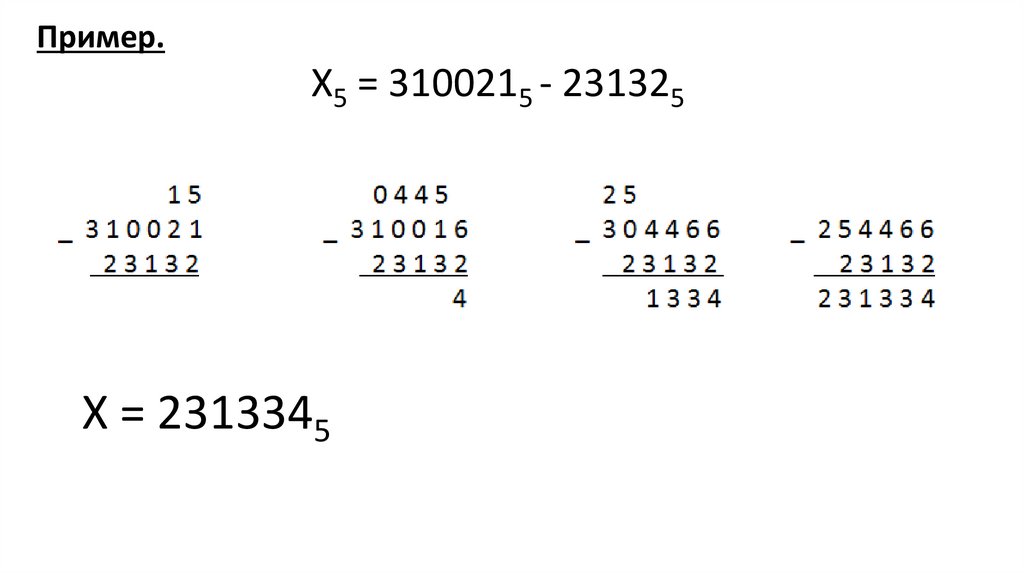






















 informatics
informatics








