Similar presentations:
Определение целого неотрицательного числа
1.
Определениецелого
неотрицательного
числа
2.
Из историиПонятие «число» является одним из основных
понятий в математике.
Числа возникли из жизненной потребности
человека и претерпели длительный путь
исторического развития.
3.
1 этапЛюди не умели считать, но была необходимость
сравнить конечные одновременно обозримые множества.
Например:
• сравнить членов семьи и количество кусков еды;
• группу охотников и количество орудий для охоты, и др.
Чтобы сравнить конечные множества, устанавливали
взаимно однозначное соответствие между данными множествами.
Например:
• о численности группы из двух предметов говорили: «Столько
же, сколько рук у человека»,
• о множестве из пяти предметов - «столько же, сколько
пальцев на руке».
Численность предметов воспринималась без их пересчета.
4.
Люди не умели измерять, но была необходимостьсравнить между собой различные объекты.
Например:
• шкуры животных, емкости, и др.
Чтобы сравнить различные объекты, устанавливали
соответствие между объектами.
Например:
• шкуры накладывали одна на другую;
• зерно пересыпали из одной емкости в другую.
Мера объектов воспринималась без их измерения.
5.
2 этапДля сравнения множеств стали применять множествапосредники: мелкие камешки, раковины, пальцы.
Множества-посредники есть зачатки понятия
натурального числа, хотя еще число не отделяется от
сосчитываемых предметов.
Например: речь шла о пяти камешках, пяти пальцах, а не о
числе «пять» вообще.
Названия множеств-посредников стали использовать для
определения численности множеств, которые с ними
сравнивались.
Например:
Численность множества, состоящего из пяти элементов,
обозначалась словом «рука», а численность множества из 20
предметов - словами «весь человек».
6.
Для сравнения объектов стали применять меркипосредники: длина ладони, стопы, носа, палочки разнойдлины, площадь ладони, шкурки животного и др.
Мерки-посредники также есть зачатки понятия
натурального числа, хотя еще число не отделяется от
измеряемых объектов. Названия мерок-посредников стали
использовать для определения меры объектов, которые с
ними сравнивались.
Например:
шаг – средняя длина человеческого шага;
пядь – расстояние между концами расставленных пальцев.
7.
3 этапНаучившись оперировать множествами-посредниками,
мерками-посредниками человек установил то общее, что
существует, например, между пятью пальцами и пятью
яблоками, пятью пядями.
Произошло отвлечение от природы элементов множествпосредников или мерок-посредников, возникло
представление о натуральном числе.
При счете или измерении проговаривались слова «один»,
«два» и т.д., а не перечислялись «одно яблоко», «два
яблока».
Историки считают, что произошло это в каменном веке, в
эпоху первобытнообщинного строя, примерно в 10-5
тысячелетии до н.э.
Этот этап связан с называнием числа.
8.
4 этапПостепенно люди научились не только называть числа, но и
обозначать их, а также выполнять над ними действия.
Натуральный ряд чисел возник не сразу, история его
формирования длительная.
Запас чисел, которые употребляли, ведя счет, увеличивался
постепенно.
Постепенно сложилось и представление о бесконечности
множества натуральных чисел.
Например:
В работе «Псаммит» - исчисление песчинок древнегреческий математик Архимед (III в. до н. э,) показал,
что ряд чисел может быть продолжен бесконечно, и описал
способ образования и словесного обозначения сколь угодно
больших чисел.
9.
5 этапЧтобы вести счет или производить измерения, нужна
последовательность числительных, которая:
• начинается с единицы
• позволяет осуществлять переход от одного числительного к
другому, при чем, столько раз, сколько это необходимо.
Следовательно:
Необходимо обосновать систему натуральных чисел как
некую теорию, в которой в первую очередь следует ответить
на вопрос, что же представляет собой число как элемент
натурального ряда.
10.
С возникновением понятия натурального числа появиласьвозможность изучать эти числа независимо от тех
конкретных задач, в связи с которыми они возникли.
Теоретическая наука, которая стала изучать числа и действия
над ними, получила название «арифметика».
Арифметика возникла в странах Древнего Востока:
Вавилоне, Китае, Индии и Египте.
Накопленные в этих странах математические знания были
развиты и продолжены учеными Древней Греции.
В средние века большой вклад в развитие арифметики
внесли математики Индии, стран арабского мира и Средней
Азии, а начиная с XIII века - европейские ученые.
11.
Термин «натуральное число» впервые употребил в V в.римский ученый А. Боэций.
Во второй половине XIX века натуральные числа оказались
фундаментом всей математической науки.
Появилась необходимость в строгом логическом
обосновании понятия натурального числа, в систематизации
того, что с ним связано.
Была разработана аксиоматическая теория натурального
числа.
12.
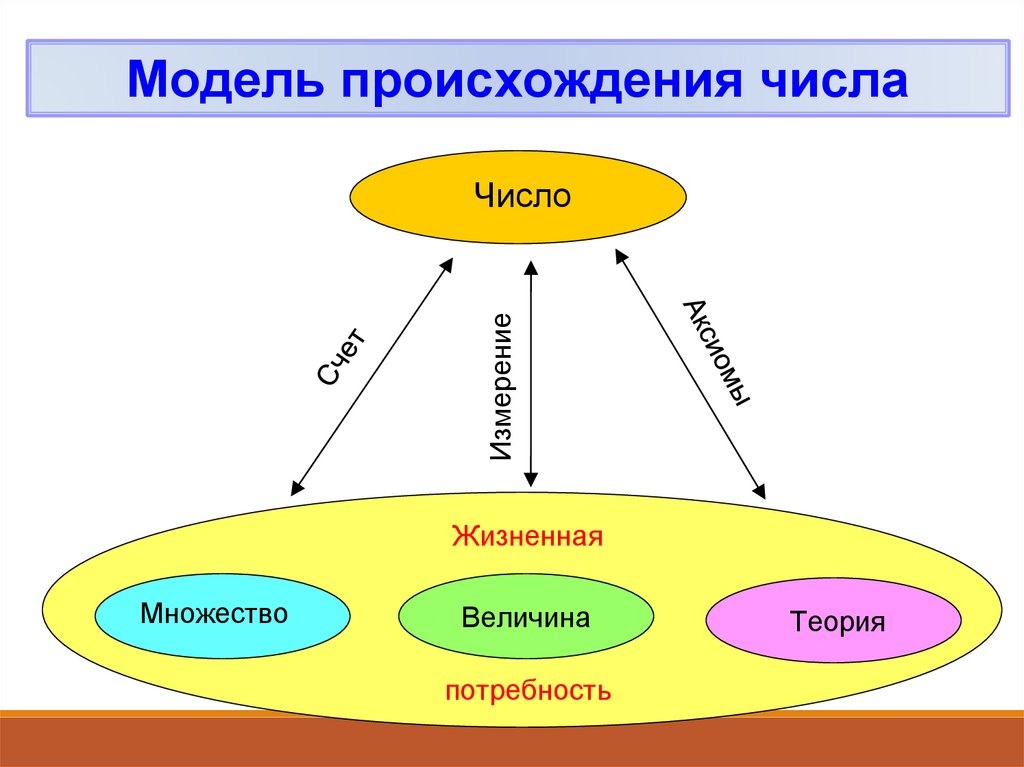
Модель происхождения числаИзмерение
Число
Жизненная
Множество
Величина
потребность
Теория
13.
Аксиоматический подходАксиоматический метод в
математике
Математические понятия, как правило,
проходят длительный путь
исторического развития.
Первоначально они возникают в
процессе решения практических
задач.
14.
При этом понятия не имеют еще строгихопределений. Даются расплывчатые
приблизительные пояснения, указания на
наглядные представления.
15.
Следующий этап в развитии математическихпонятий наступает, когда место наглядных
рассмотрений занимают рассуждения,
отличающиеся, однако, отсутствием строгой
логичности.
Возникает необходимость в уточнении
понятий, установлении связей между
ними, в сведении сложных понятий к более
простым.
16.
При аксиоматическом построениикакой-нибудь теории поступают так:
Выбирают некоторые объекты, изучаемые
теорией, и некоторые отношения между ними.
Эти объекты и отношения не определяются, а
принимаются за исходные и называются
основными (неопределяемыми)
понятиями рассматриваемой теории.
Каждое понятие, которое не содержится в
списке основных, должно быть определено.
17.
Вслед за основными понятиями иотношениями формулируются основные
предложения, их называют аксиомами,
которые в данной теории принимаются без
доказательства, и на их основе
доказываются другие предложения данной
теории – теоремы. В аксиомах дается
описание отношений между основными
понятиями, они представляют по существу
неявные определения основных понятий.
Каждое предложение рассматриваемой
теории, которого нет в списке аксиом,
должно быть доказано на основе аксиом и
ранее доказанных теорем.
18.
Система аксиом должна быть:а) непротиворечивой, т.е. мы должны быть
уверены, что делая всевозможные выводы из
данной системы аксиом никогда не придем к
противоречию;
б) независимой, т.е. никакая аксиома не должна
быть следствием остальных аксиом этой
системы;
в) полной, т.е. в рамках системы всегда можно
доказать или данное утверждение или его
отрицание.
Первым опытом аксиоматического
построения теории можно считать изложение
геометрии Евклидом в его «Началах».
19.
Аксиоматическое определениенатурального числа
Как и все математические понятия,
натуральные числа возникли из потребностей
практики.
Со временем люди научились не только
называть числа, но и обозначать их, а также
выполнять над ними действия. Многие
трудности в решении этих проблем были
преодолены с созданием в Древней Индии
десятичной системы записи чисел и понятия
нуля.
20.
Наука, которая изучает числа и действия надними, получила название «арифметика» - от
греческого аrithmos - «число».
Во второй половине 19 века натуральные
числа оказались фундаментом всей
математической науки, от состояния которого
зависела и прочность всего здания
математики. Внимание ученых было
обращено на построение и логическое
обоснование математических теорий числа.
21.
Аксиоматическая теориянатурального числа была
построена Джузеппе
Пеано (1858-1932)
В качестве основного
(неопределяемого)
отношения во множестве
N взято отношение
«непосредственно
следовать за»
Известными также считаются понятия
множества и другие теоретико-множественные
понятия, а также правила логики.
22.
Элемент, непосредственно следующий заэлементом а, обозначается а´
Отношение «непосредственно следовать за»
удовлетворяет следующим аксиомам:
А1. Во множестве N существует
элемент, непосредственно не
следующий ни за каким элементом
этого множества. Называют его
единицей
23.
А2. Для каждого элемента а измножества N существует
единственный элемент а´,
непосредственно следующий за а
24.
А3. Для каждого элемента а измножества N существует не более
одного элемента, за которым
непосредственно следует а
25.
А4. Если множество М естьподмножество множества N, и:
а) единица содержится в М;
б) из того что а содержится в М,
следует, что и а´ содержится в М, то
множество М совпадает с
множеством N.
а) 1∈М
б) а∈М ⇒ а' ∈ М
⇒ М=N
26.
Множество N, для элементов которогоустановлено отношение
«непосредственно следовать за»,
удовлетворяющее аксиомам 1- 4,
называется множеством
натуральных чисел, а его элементы –
натуральными числами.
27.
Выбирая в качестве множества N некотороеконкретное множество, на котором задано
конкретное отношение «непосредственно
следовать за», удовлетворяющее аксиомам 1-4,
получают различные интерпретации (модели)
данной системы аксиом:
1) ряд чисел 1, 2, 3, …
2) {O O}, {O О O}, {O O О О}, …
28.
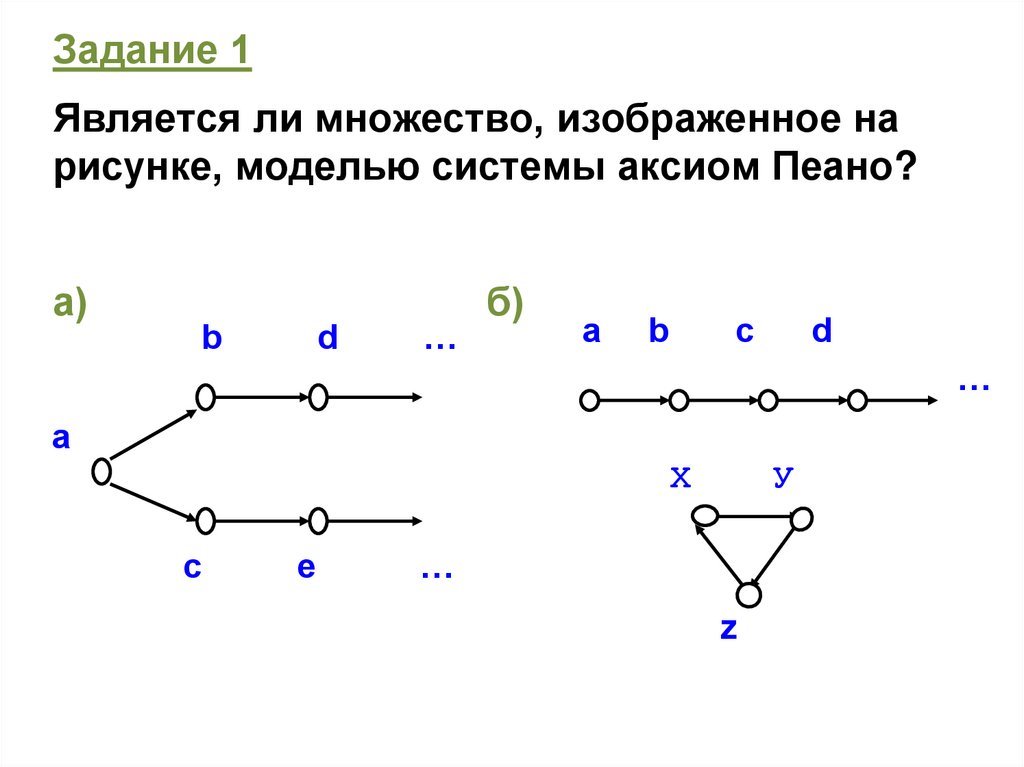
Задание 1Является ли множество, изображенное на
рисунке, моделью системы аксиом Пеано?
а)
b
d
…
б)
а
b
с
d
…
а
Х
с
е
У
…
z
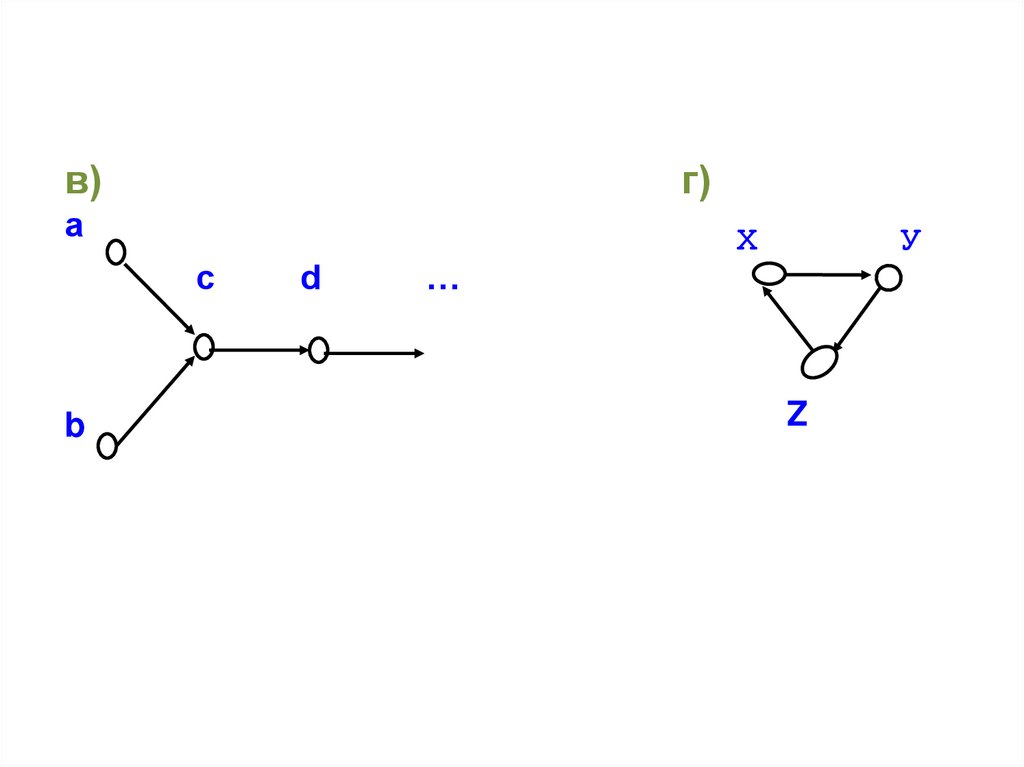
29.
в)г)
а
Х
с
b
d
У
…
Z
30.
Отношение «непосредственнопредшествовать»
Если натуральное число b непосредственно
следует за натуральным числом а, то число а
называется непосредственно предшествующим
(или просто предшествующим) числу b.
Свойства отношения «непосредственно
предшествовать»
1. Единица не имеет предшествующего
натурального числа
2. Каждое натуральное число а ≠ 1, имеет
предшествующее число b, такое, что b' = а
31.
Множество целых неотрицательных чиселОбозначают Z0 или N0
N0 = N ∪ {0}
0, 1, 2, 3, …
Множество N0 удовлетворяет всем
аксиомам Пеано.
32.
Те свойства отношения «непосредственноследовать за, которые отражены в
аксиомах 1 – 4, изучаются в начальных
классах и используются при решении
задач. Уже в 1 классе при рассмотрении
чисел первого десятка выясняется, как
может быть получено каждое число. При
этом широко используются понятия
«следует», «предшествует», прибавление и
вычитание 1.
33.
Каждое новое число с самого начала выступает какпродолжение ранее изученного отрезка натурального
ряда чисел.
Любое натуральное число может быть получено
прибавлением 1 к тому числу, которое встречается при
счете перед ним, или вычитанием 1 из числа, которое
идет при счете сразу после него.
Любое число на 1 больше предшествующего.
Таким образом, уже в начальных классах учащиеся
убеждаются в том, что за каждым числом идет следующее и
притом только одно, что натуральный ряд чисел бесконечен.
34.
Задание 2Покажите, что множество целых
неотрицательных чисел является моделью
системы аксиом Пеано. Какое число
выполняет при этом роль единицы?
Можно ли считать моделью системы аксиом
Пеано множество 3, 4, 5, 6, …? множество 3,
6, 9, 12, …?
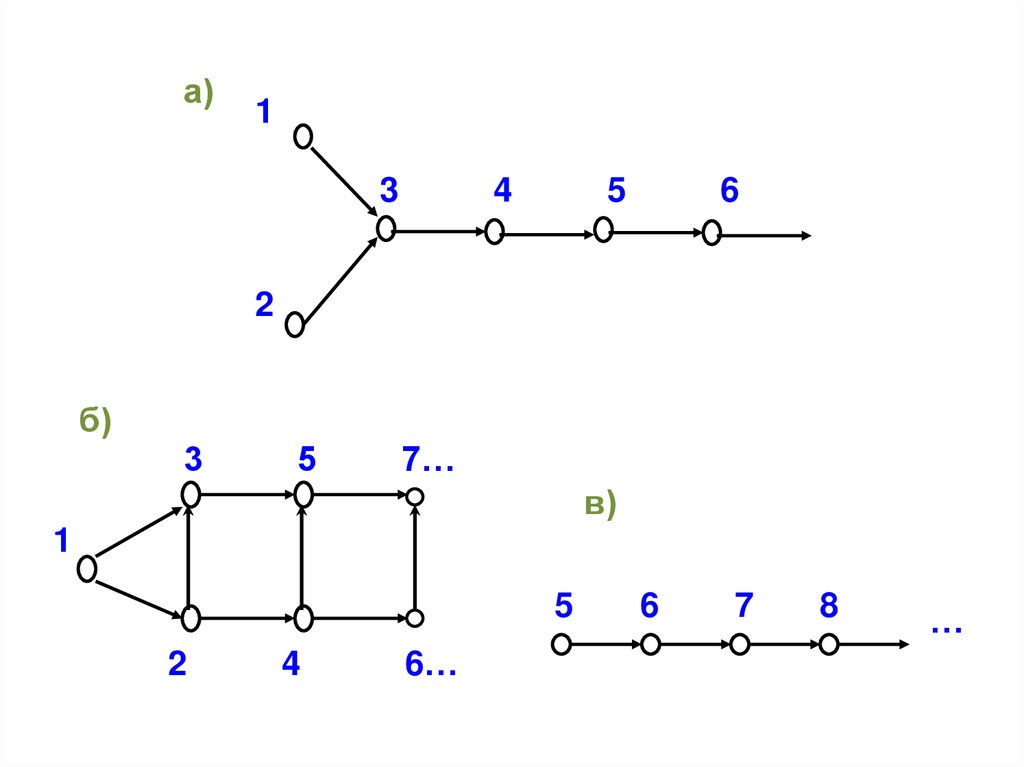
Задание 3
Установите, какие из множеств,
приведенных на рисунке, являются
моделями системы аксиом Пеано.
35.
а)1
3
4
5
6
2
б)
3
5
7…
в)
1
5
2
4
6…
6
7
8
…
36.
Теоретико-множественный подходСчет
Порядковые и количественные
натуральные числа
37.
12
3
5
6
4
38.
Требования, соблюдаемые при счете:- первому отмеченному предмету ставится в
соответствие число 1;
- каждый раз отмечается предмет еще не
отмеченный ранее, и ему ставится в
соответствие число, следующее за последним
из уже названных.
Таким образом, каждому из сосчитанных
предметов поставлено в соответствие одно
число, двум разным предметам
соответствуют различные числа.
39.
Сущность счета заключается вустановлении взаимно
однозначного соответствия между
множествами, подлежащими счету,
и некоторым отрезком
натурального ряда. Процесс счета
закончится тогда и только тогда,
если считаемое множество конечно
1
2
3
4
5
6
40.
Отрезком Nа натурального ряданазывается множество натуральных
чисел, не превосходящих
натурального числа а
Nа = {х | х∈Ν и х ≤ а} или
Nа = {1, 2, 3, …, а}
N3 = {1, 2, 3}
N6 = {1, 2, 3, 4, 5, 6}
41.
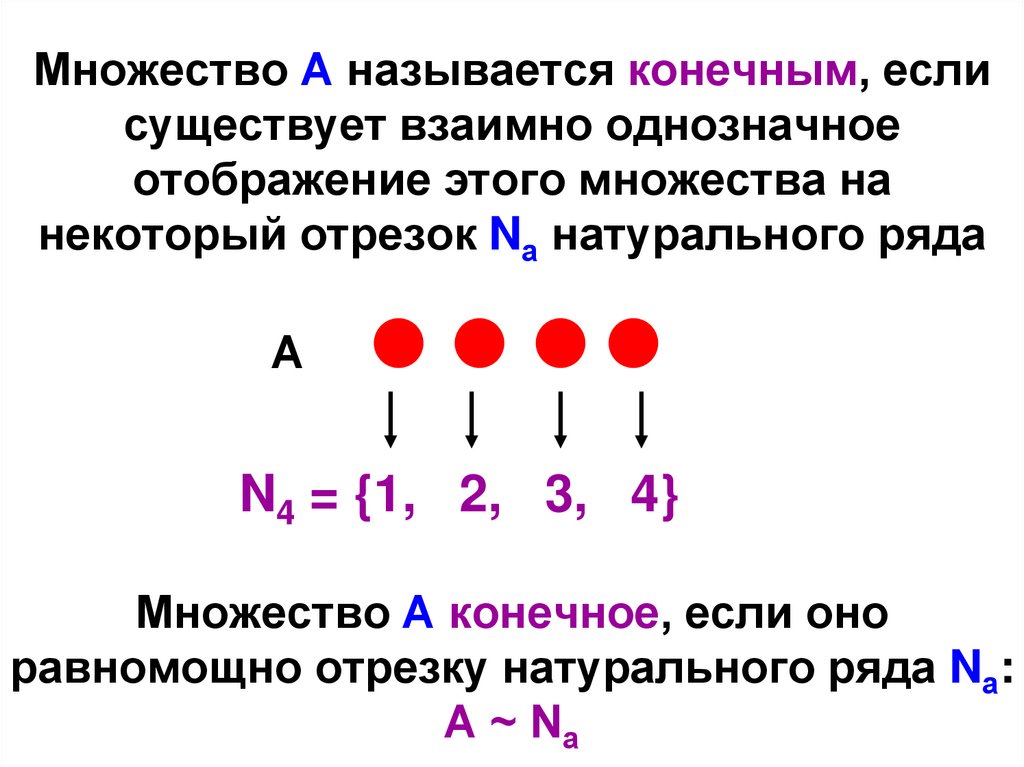
Множество А называется конечным, еслисуществует взаимно однозначное
отображение этого множества на
некоторый отрезок Nа натурального ряда
А
N4 = {1, 2, 3, 4}
Множество А конечное, если оно
равномощно отрезку натурального ряда Nа:
А ~ Nа
42.
Одно и то же множество А не может бытьвзаимно однозначно отображено на два
различных отрезка натурального ряда
Множество А равномощно только
одному отрезку натурального ряда Nа, и
поэтому множеству А может быть
поставлено в соответствие
единственное число а. Это число а
называют числом элементов в
множестве А и пишут: n(А) = а –
количественное натуральное число
43.
Пример: Множество А = {а, b, с} можновзаимно однозначно отобразить на
отрезок натурального ряда N3. Поэтому
n(А) = 3
Взаимно однозначное отображение
множества А на отрезок Nа можно
понимать как нумерацию элементов
множества А. Этот процесс
нумерации называют счетом.
44.
Существует много нумераций одного итого же множества:
a→1
b→1
c→1
b→2
a→2
b→2
c→3
c→3
a→3
c→1
a→1
b→1
a→2
c→2
c→2
b→3
b→3
a→3
45.
При пересчете элементы конечногомножества расставляются в
определенном порядке, а также
устанавливается, сколько элементов
содержит множество. В первом случае
натуральное число представляет собой
порядковый номер некоторого элемента и
называется числом порядковым (первый,
второй, третий и т.д.). Во втором случае
мы имеем дело с числом количественным
(один, два, три и т. д.)
46.
ОпределениеС теоретико-множественных
позиций натуральное число
рассматривается как число
элементов конечного
множества
n(∅) = 0
47.
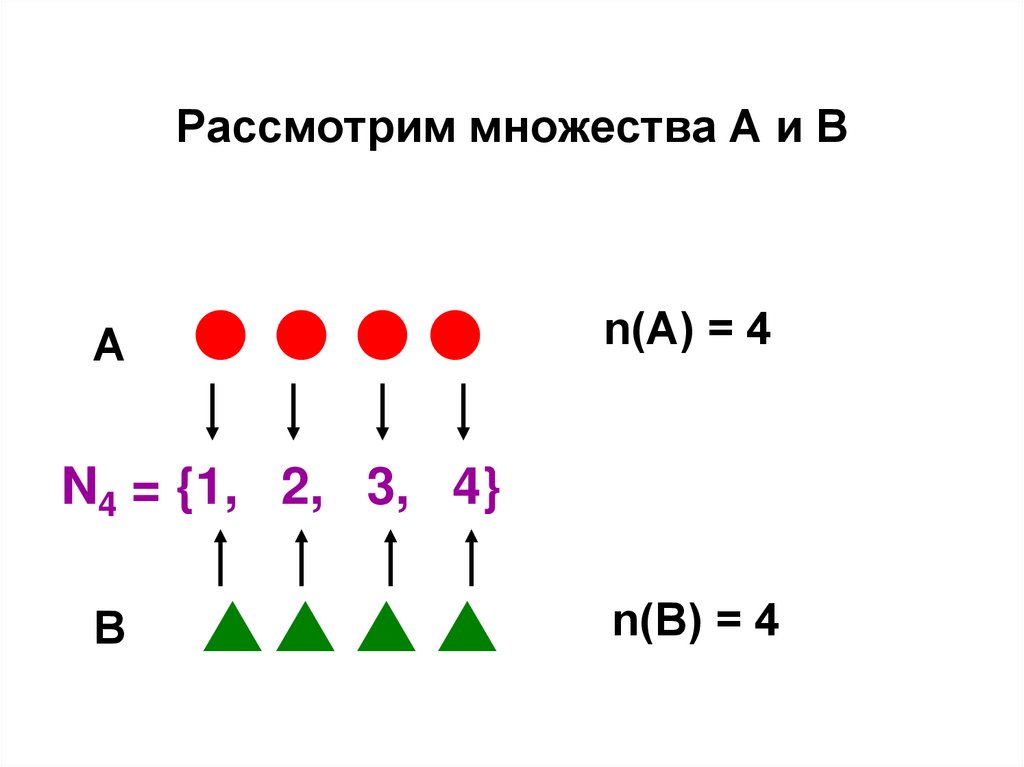
Рассмотрим множества А и ВА
n(А) = 4
N4 = {1, 2, 3, 4}
В
n(В) = 4
48.
Следующие предложения равносильны:- Множествам А и В соответствует одно и
то же число а
- Множества А и В равномощны (А ~ В)
- Множества А и В содержат поровну
элементов
- Множества А и В можно взаимно
однозначно отобразить на один и тот же
отрезок натурального ряда Nа
- Множества А и В можно взаимно
однозначно отобразить друг на друга
49.
Так как одному и тому же конечномумножеству может соответствовать
лишь одно натуральное число а, то
вся совокупность конечных
множеств распадается на классы
равномощных множеств.
Каждое множество данного класса
содержит по а элементов.
Nа принадлежит данному классу
50.
Количественное натуральное числорассматривается как общее свойство
класса конечных равномощных
множеств
51.
Задание 41) Запишите все элементы множества: N7, N11,
N14.
2) Какие из указанных ниже множеств
являются отрезками натурального ряда:
а) {1, 2, 3, 4, 5}, б) {0, 1, 2, 3}, в) {3, 4, 5, 6, 7},
г) {4, 2, 1, 5, 3}?
3) Какими порядковыми числами задаются
элементы множества: а) А = {a, b, c, d, e, f},
б) элементы множества букв слова
«количество»?
4) Каков теоретико-множественный смысл
натурального числа 7?
52.
5) Приведите примеры класса множеств,соответствующих натуральному числу:
а) 5, б) 10, в)12.
6) При знакомстве с числом «2» учитель
использовал различные картинки с
изображением двух предметов. Можно ли
так поступать при изучении других чисел?
Ответ обоснуйте.
7) Прочитайте записи: n(А) = 5, n(В) = 0.
Приведите примеры множеств А и В,
удовлетворяющих этим условиям.
8) Придумайте множества В и С, для
которых выполняются условия:
а) n(В) = n(С), В ≠С,
б) n(В) = n(С), В = С.
53.
9) Докажите, что множество А – конечное, если:а) А – множество букв в слове
«параллелограмм»;
б) А – множество учащихся в классе;
в) А – множество букв в учебнике
математики.
54.
Натуральное число как результатизмерения величин
Натуральные числа используют не
только для пересчета элементов
конечных множеств, но и для
измерения величин: длин отрезков,
площадей фигур, масс тел и др.
Рассмотрим натуральное число как
результат измерения длины отрезка
55.
Считают, что отрезок а разбит наотрезки (состоит из отрезков) а1, а2, …,
аn, если он является их объединением
и никакие два из отрезков не имеют
общей внутренней точки, хотя и могут
иметь общие концы. В этом случае
отрезок а называют суммой отрезков
а1, а2, …, аn и пишут:
а = а1 + а2 + … + аn
а1
а2 а3 а4
а
а5
а = а1 + а2 + а3 + а4 + а5
56.
Выберем из множества отрезковнекоторый отрезок е и назовем его
единичным отрезком или единицей
длины
Если отрезок а можно разбить на n
отрезков, каждый из которых равен
единичному отрезку е, то число n
назовем мерой или значением длины
отрезка а при единице длины е и будем
писать: n = mе(а) или а=nе.
Говорят также, что отрезок а кратен
отрезку е
57.
ае1
mе1(а) = 12 или а = 12 е1
е2
mе2(а) = 6 или а = 6 е2
е3
mе3(а) = 3 или а = 3 е3
При переходе к другой единице длины
мера отрезка меняется, хотя сам
отрезок остается неизменным
58.
Натуральное число как мераотрезка а показывает, из
скольких выбранных единичных
отрезков е состоит отрезок а
При выбранной единице длины е для
отрезка а это число единственное
59.
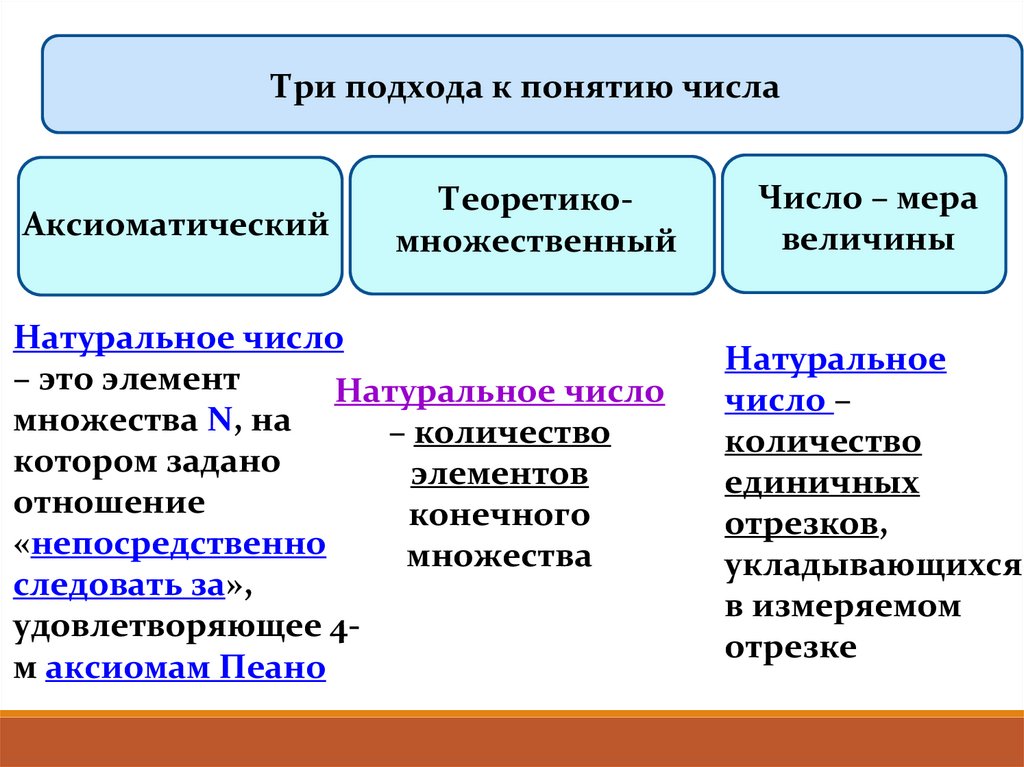
Три подхода к понятию числаАксиоматический
Теоретикомножественный
Натуральное число
– это элемент
Натуральное число
множества Ν, на
– количество
котором задано
элементов
отношение
конечного
«непосредственно
множества
следовать за»,
удовлетворяющее 4м аксиомам Пеано
Число – мера
величины
Натуральное
число –
количество
единичных
отрезков,
укладывающихся
в измеряемом
отрезке




















































 mathematics
mathematics








