Similar presentations:
Теорема о трех перпендикулярах. Геометрия. 10 класс
1.
2.
Теорема о трех перпендикулярах.Прямая, проведенная в плоскости через основание
наклонной перпендикулярно к ее проекции на эту
плоскость, перпендикулярна и к самой наклонной.
А
П-Р
Н
Н-я
П-я
М
a
3.
Обратная теорема.Прямая, проведенная в плоскости через основание
наклонной перпендикулярно к ней,
перпендикулярна и к ее проекции.
А
П-Р
Н
Н-я
П-я
М
a
4. Применение знаний в стандартной ситуации
5.
Прямая АК перпендикулярна к плоскости правильноготреугольника АВС, а точка М – середина стороны ВС.
Докажите, что МК ВС.
№148.
К
П-Р
А
В
П-я
М
С
BC AМ
П-я
BC MК
TTП
Н-я
6.
Отрезок АD перпендикулярен к плоскости равнобедренноготреугольника АВС. Известно, что АВ = АС = 5 см, ВС = 6 см,
АD = 12 см.
Найдите расстояния от концов отрезка АD до прямой ВС.
№149 (дом.)
D
П-Р
В
12
П-я
А
N 6
5
С
BC AN
П-я
BC DN
TTП
Н-я
АN и DN – искомые расстояния
7.
В треугольнике угол С прямой, угол А равен 600, AС=12см.DC (АВС). DC= 6 5 Найдите расстояния:
а) от точки С до прямой АВ, б) от точки D до прямой АВ.
АВ СN
D
AB DN
TTП
Н-я
П-я
6 5
CN и DN – искомые расстояния
П-Р
12
С
А
600
N
В
8.
Через вершину прямого угла С равнобедренногопрямоугольного треугольника АВС проведена прямая СМ,
перпендикулярная к его плоскости. Найдите расстояние от
точки М до прямой АВ, если АС = 4 см, а СМ = 2 7 см.
№155.
М
П-Р
2 7
С
А
4
П-я
F
В
AВ СF
П-я
AВ MF
TTП
Н-я
МF – искомое расстояние
9.
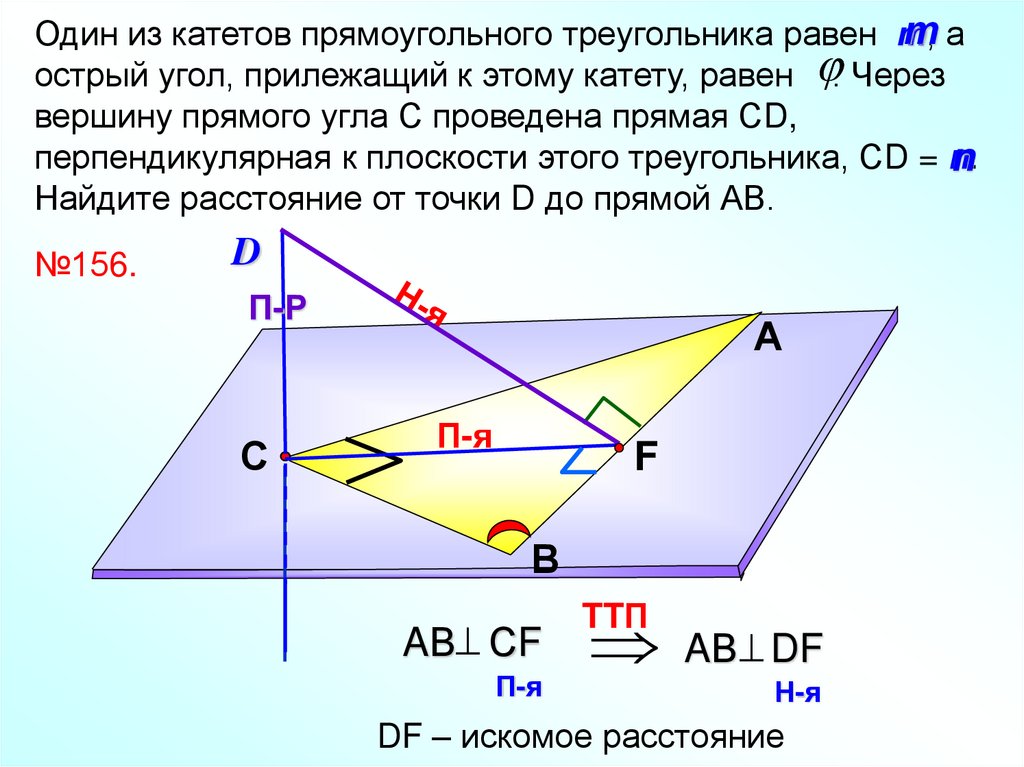
таОдин из катетов прямоугольного треугольника равен т,
острый угол, прилежащий к этому катету, равен . Через
вершину прямого угла С проведена прямая СD,
перпендикулярная к плоскости этого треугольника, СD = n.
n
Найдите расстояние от точки D до прямой АВ.
№156.
D
П-Р
С
А
П-я
F
В
AВ СF
П-я
AВ DF
TTП
Н-я
DF – искомое расстояние
10. Подведение итогов Домашнее задание
• Пункты 19,20• №№, 143,









 mathematics
mathematics








