Similar presentations:
التوزيع الإلكتروني والأرقام الكمية
1.
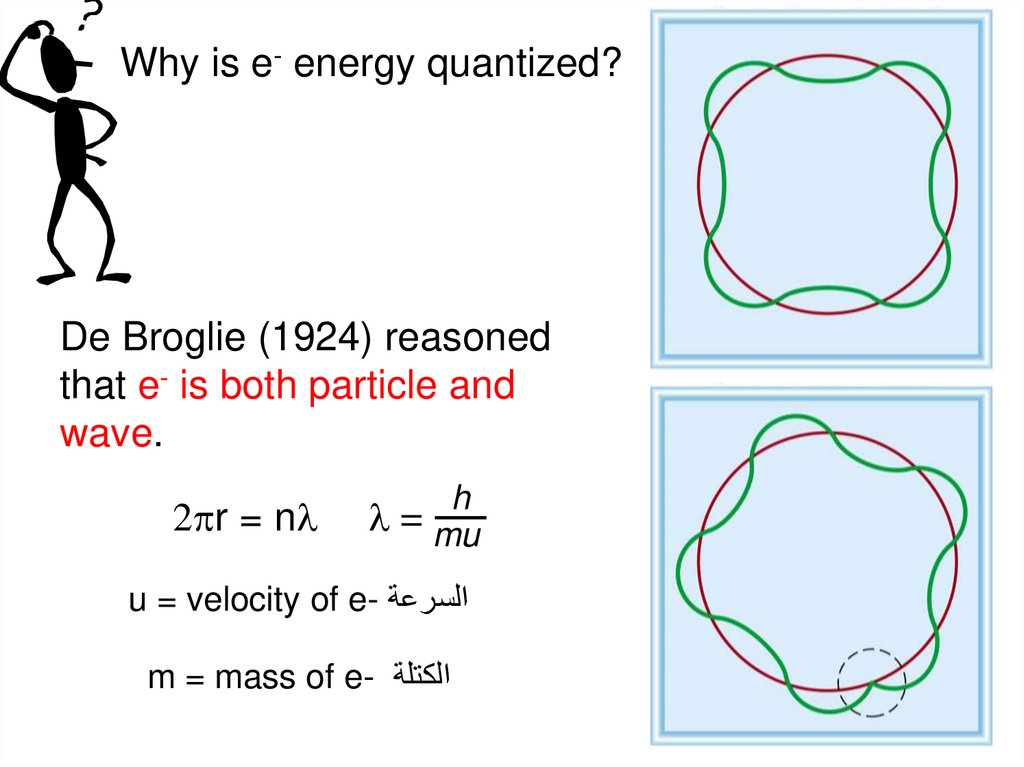
Why is e- energy quantized?De Broglie (1924) reasoned
that e- is both particle and
wave.
2pr = nl
h
l = mu
u = velocity of e- السرعة
m = mass of e- الكتلة
2.
What is the de Broglie wavelength (in nm)associated with a 2.5 g Ping-Pong ball
traveling at 15.6 m/s?
l = h/mu
h in J•s m in kg
u in m/s
l = 6.63 x 10-34 / (2.5 x 10-3 x 15.6)
l = 1.7 x 10-32 m = 1.7 x 10-23 nm
3.
( )1طول موجة طيف ذرة الهيدروجين عند انتقال اإللكترون من المستوى n = 3إلىالمستوى :n = 2
(657 nmأ)
(487.8 nmب)
(758.1 nmج)
(857.8 nmد)
( )2يحدث إنبعات أشعة مرئية وفوق بنفسجية من ذرات:
(أ) عندما تنتقل اإللكترونات من مستويات طاقة منخفضة لمستويات أعلى.
(ب) عندما تتكاثف الذرات من غاز لسائل.
(ج) عندما تنتقل اإللكترونات من مستويات طاقة عالية لمستويات منخفضة.
(د) عندما يتنقل اإللكترون داخل مدار الذرة.
4.
5.3طبيعة اإللكترونThe Dual Nature of Electron
يمكن أعتبار اإللكترون بأنه جسيم له كتلة
وكذلك موجة له خواص كهرومغناطيسية
وعليه توجد عالقة فيما بين كتلة اإللكترون وإعتباره موجه بتطبيق العالقة
الرياضية التالية:
)l (m)= h (J.s) ÷ m (kg). u (m/s
حيث أن = m :كتلة اإللكترون و = uسرعته والندا = lطول موجته
)(1 J = 1 kg. m2/s2
مثال :صفحة 282في المرجع المعتمد لمقرر ك .110
5.
: هو2.0 x 105 m/s الذي سرعته20Ne+ ) الطول الموجي أليون النيون1()19.992 amu (علما ُ بأن الوزن الذري للنيون هو
A.1.0 10-13 m
B.1.0 10-16 m
C.1.0 10-18 m
D.9.7 1012 m
: هو10.0 cm/s وسرعتها10.0 gm ) طول موجة كرة كتلتها2(
A. 6.63 10-22 nm
B. 6.63 1013 nm
C. 6.63 10-31 nm
D. 6.63 1022 nm
: هو9.1 x 10-28 g وكتلته تساوي7 x 103 km/s ) طول موجة إلكترون سرعته3(
A. 1.0 x 10-13 m
B. 1.0 x10-7 m
C. 1.0 m
D. 1.0 x10-10 m
l (m) = h (J.s) ÷ m (kg). u (m/s) = h (Kg.m2/s2).s ÷ U (kg) . U (m/s)
1 J = 1 kg. m2/s2
Mass of the electron = 9.11 x 10-31 kg
Frequency constant B/h = 3.289 x 1015 s-1
Energy constant for H atom = 2.179 x 10-18 J
6.
5.4المدارات الذريةAtomic Orbitals
) (1أقصى سعة إلشغال المجال اإللكتروني :إلكترونان ويمكن أن يشغل بإلكترون واحد أو يظل فارغا.
ويرمز للمجال بدائرة أو مربع ولإللكترون بسهم.
مشغول
بإلكترونين
مشغول
بإلكترون
فارغ
) (2توجد فروق بين المجاالت اإللكترونية سواء كانت من نفس النوع أو من أنواع
مختلفة:
المجاالت ) :(1s, 2s, 3sكلها كروية الشكل والفرق بينها أنها تزداد بعدا عنالنواة بزيادة عدد الكم الرئيسي للمجال (رقم المستوى الطاقي).
7.
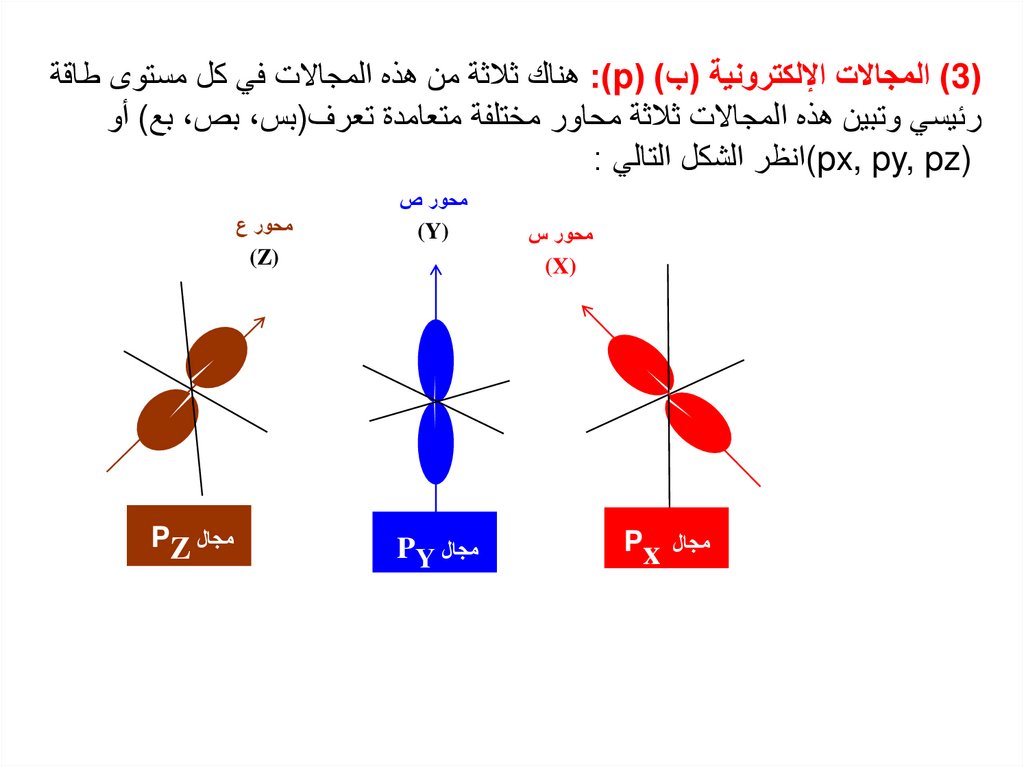
( )3المجاالت اإللكترونية (ب) ( :)pهناك ثالثة من هذه المجاالت في كل مستوى طاقةرئيسي وتبين هذه المجاالت ثالثة محاور مختلفة متعامدة تعرف(بس ،بص ،بع) أو
)(px, py, pzانظر الشكل التالي :
محور ص
محور س
)(Y
)(Z
)(X
مجال Px
محور ع
مجال PY
مجال PZ
8.
دوران اإللكترون في اتجاه عقارب الساعة أو في عكس اتجاه عقارب الساعةدوران اإللكترون حول نفسه:
دوران اإللكترون
)(1يدور اإللكترون حول نفسه باإلضافة إلى دورانه
حول النواة.
) (2دوران اإللكترون حول نفسه أما أن يكون في اتجاه
في اتجاه عقارب الساعة
دوران عقارب الساعة 0.5 + =msأو بعكس اتجاه
في عكس اتجاه عقارب
عقارب الساعة ( 0.5 - =msانظر الشكل).
الساعة
) (3يكون اإللكترون الذي يدور حول نفسه حقال مغناطيسيا يعتمد اتجاهه
على اتجاه دورانه.
) (4يمكن أن يشغل إلكترونان مجاال إلكترونيا واحدا بشرط أن يكون
دوران أحدهما حول نفسه في اتجاه عقارب الساعة واآلخر في عكس
اتجاه عقارب الساعة .وينشأ عن ذلك حقالن مغناطيسيان متعاكسان
في االتجاه ينتج عنهما قوة تجاذب بين اإللكترونين تتغلب على قوة
التنافر بينهما بسبب شحنتهما السالبة.
9.
5.5االعداد الكميةQuantum Numbers
طاقة اإللكترونات وتوزيعها:
) (1تتوزع اإللكترونات حول النواة في مستويات طاقة رئيسية (يطلق عليه
بأسم رقم الكم الرئيسي) :تعطى لها الحروف ].[K, L, M, N, O, P, Q
) (2لكل مستوى طاقة رئيسي عدد كم رئيسي )(Principal Quantum Number
وهو العدد الذي يحدد رقم مستوى الطاقة الرئيسي في الذرة ويرمز له بالرمز
( )nويكون دائما ً عددا ً صحيحا ً ويأخذ القيم ( .).....،6 ،5 ،4 ،3 ،2 ،1
) (3تعتمد طاقة اإللكترونات على عدد الكم الرئيسي (:)n
فاإللكترونات في مستوى الطاقة الرئيسي األول ( )1 = nتمتلك أقل قدر من
الطاقة .وتزداد طاقة اإللكترونات تباعا ً بزيادة عدد الكم الرئيسي ( )nالذي تقع
فيه اإللكترونات.
10.
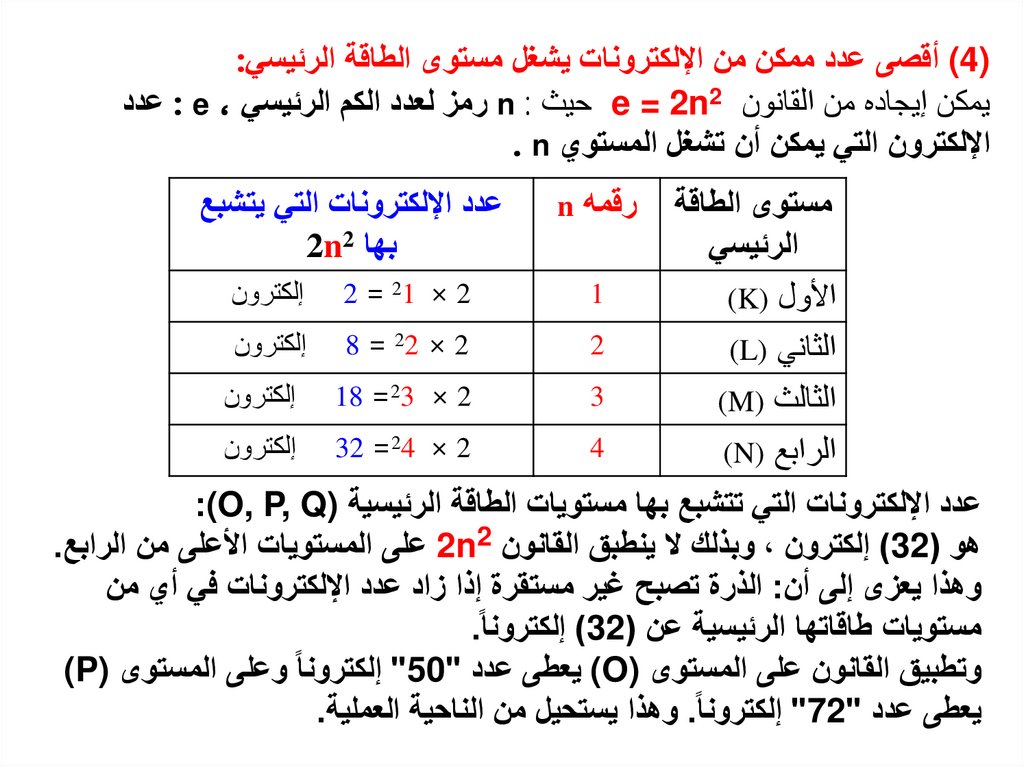
) (4أقصى عدد ممكن من اإللكترونات يشغل مستوى الطاقة الرئيسي:يمكن إيجاده من القانون e = 2n2حيث n :رمز لعدد الكم الرئيسي : e ،عدد
اإللكترون التي يمكن أن تشغل المستوي . n
مستوى الطاقة
الرئيسي
األول )(K
الثاني )(L
الثالث )(M
الرابع )(N
رقمه n
عدد اإللكترونات التي يتشبع
بها 2n2
1
2 = 21 × 2
إلكترون
2
8 = 22 × 2
إلكترون
3
18 =23 × 2
إلكترون
4
32 =24 × 2
إلكترون
عدد اإللكترونات التي تتشبع بها مستويات الطاقة الرئيسية ):(O, P, Q
هو ( )32إلكترون ،وبذلك ال ينطبق القانون 2n2على المستويات األعلى من الرابع.
وهذا يعزى إلى أن :الذرة تصبح غير مستقرة إذا زاد عدد اإللكترونات في أي من
مستويات طاقاتها الرئيسية عن ( )32إلكترونا.
وتطبيق القانون على المستوى ) (Oيعطى عدد " "50إلكترونا وعلى المستوى )(P
يعطى عدد " "72إلكترونا .وهذا يستحيل من الناحية العملية.
11.
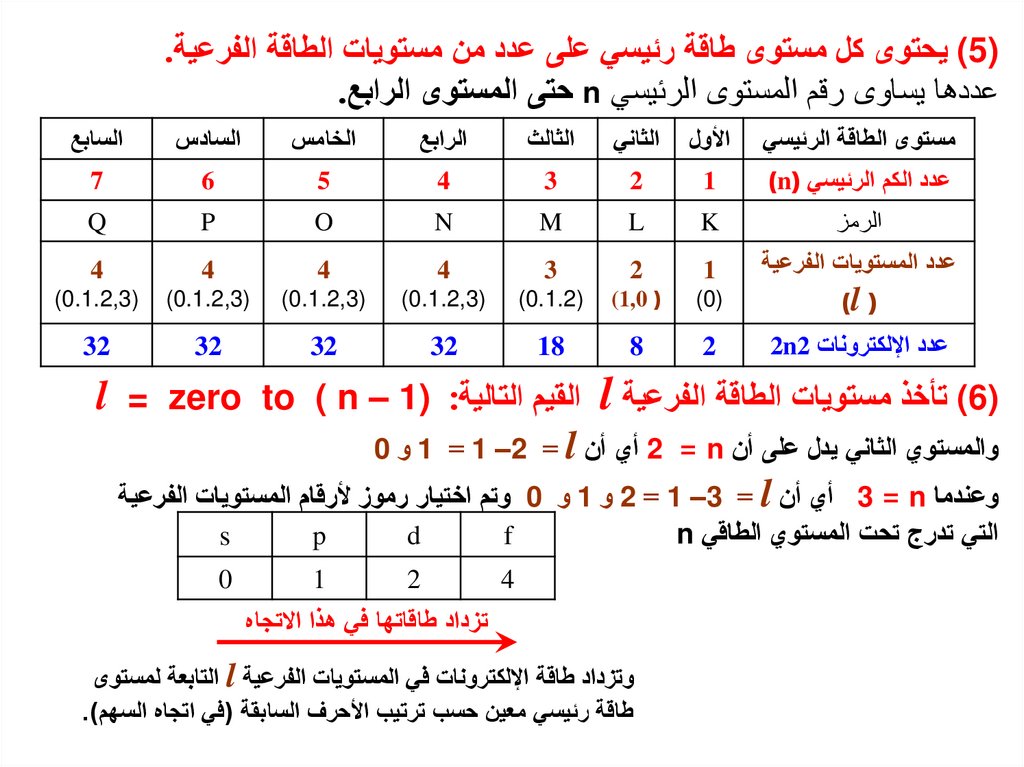
) (5يحتوى كل مستوى طاقة رئيسي على عدد من مستويات الطاقة الفرعية.عددها يساوى رقم المستوى الرئيسي nحتى المستوى الرابع.
مستوى الطاقة الرئيسي
األول
الثاني
الثالث
الرابع
الخامس
السادس
السابع
عدد الكم الرئيسي ()n
1
2
3
4
5
6
7
الرمز
K
L
M
N
O
P
Q
عدد المستويات الفرعية
1
2
( )l
)(0
( (1,0
3
4
4
4
4
)(0.1.2
)(0.1.2,3
)(0.1.2,3
)(0.1.2,3
)(0.1.2,3
عدد اإللكترونات 2n2
2
8
18
32
32
32
32
) (6تأخذ مستويات الطاقة الفرعية lالقيم التاليةl = zero to ( n – 1) :
والمستوي الثاني يدل على أن 2 = nأي أن 1 = 1 –2 = lو 0
وعندما 3 = nأي أن 2 = 1 –3 = lو 1و 0وتم اختيار رموز ألرقام المستويات الفرعية
التي تدرج تحت المستوي الطاقي n
f
d
p
s
4
2
1
0
تزداد طاقاتها في هذا االتجاه
وتزداد طاقة اإللكترونات في المستويات الفرعية lالتابعة لمستوى
طاقة رئيسي معين حسب ترتيب األحرف السابقة (في اتجاه السهم).
12.
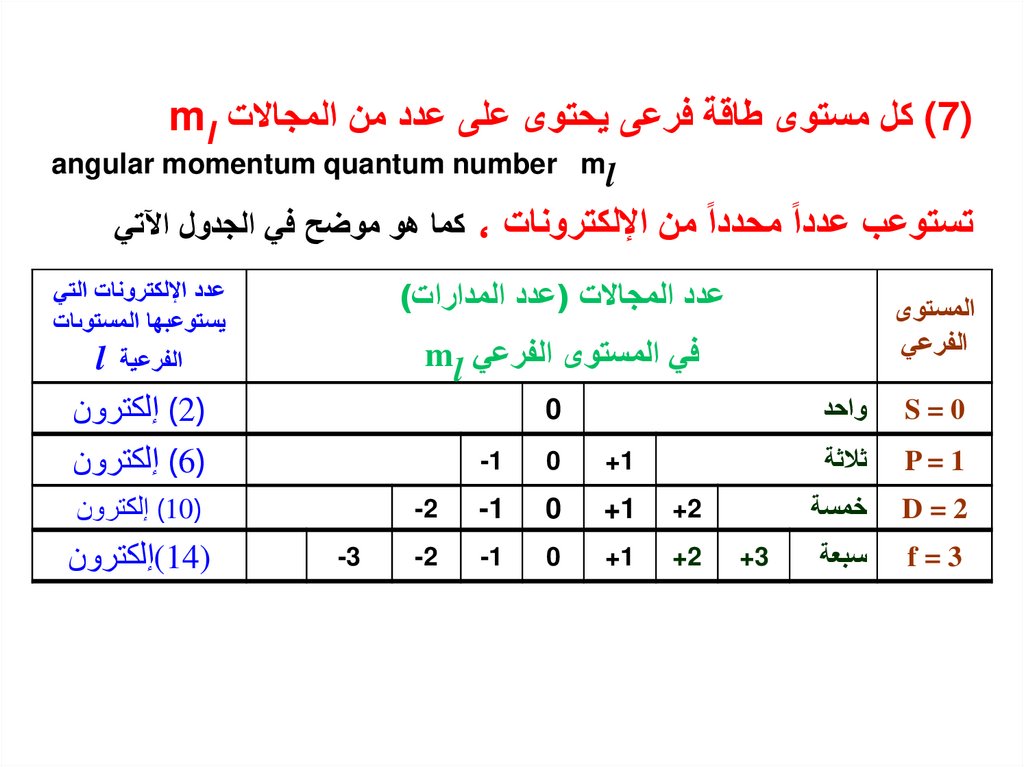
) (7كل مستوى طاقة فرعى يحتوى على عدد من المجاالت mlangular momentum quantum number ml
تستوعب عددا محددا من اإللكترونات ،كما هو موضح في الجدول اآلتي
المستوى
الفرعي
S=0
واحد
P=1
ثالثة
D=2
خمسة
f=3
سبعة
+3
عدد المجاالت (عدد المدارات)
في المستوى الفرعي ml
عدد اإللكترونات التي
يستوعبها المستوىات
0
الفرعية l
( )2إلكترون
( )6إلكترون
( )10إلكترون
+1
0
-1
+2
+1
0
-1
-2
+2
+1
0
-1
-2
-3
)(14إلكترون
13.
مثال : 1أذكر أرقام الكم األربعة ألحدى إلكترونات المستوي الفرعي . 2pالحـل :
= nرقم الكم الرئيسي = 2
ورقم الكم الثانوي 1 = 1 –n = lو 0وألن اإللكترون في الـ pإذن 1 =l
وعليه توجد احتمالية وجود اإللكترون في المدار:
ml -1أو 0 mlأو ml -1
ورقم الكم المغزلي له + 0.5 = mSأو - 0.5
14.
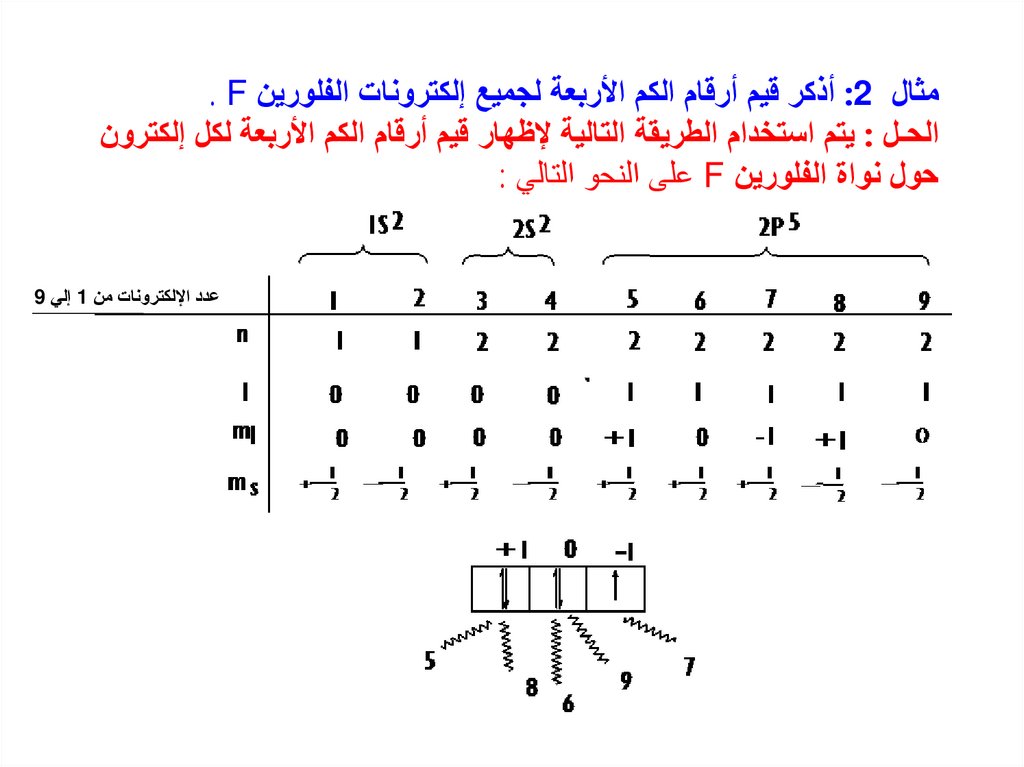
مثال :2أذكر قيم أرقام الكم األربعة لجميع إلكترونات الفلورين . Fالحـل :يتم استخدام الطريقة التالية إلظهار قيم أرقام الكم األربعة لكل إلكترون
حول نواة الفلورين Fعلى النحو التالي :
عدد اإللكترونات من 1إلي 9
15.
( )1تستخدم المعادلة الراياضية التالية :2n2(أ) لمعرفة عدد إلكترونات المستوى الفرعي
(ب) لمعرفة عدد إلكترونات المستوى الرئيسي
(ج) لمعرفة عدد المستويات الفرعية
(د) لمعرفة عدد المدارات التي بداخل كل مستوى فرعي
( )2تستخدم المعادلة الراياضية التالية : 2 l + 2
(أ) لمعرفة عدد إلكترونات المستوى الفرعي (ب) لمعرفة عدد إلكترونات المستوى الرئيسي
(د) لمعرفة عدد المدارات التي بداخل كل مستوى فرعي
(ج) لمعرفة عدد المستويات الفرعية
( )3تستخدم المعادلة الراياضية التالية : n - 1
(أ) لمعرفة عدد إلكترونات المستوى الفرعي
(ج) لمعرفة عدد المستويات الفرعية
(ب) لمعرفة عدد إلكترونات المستوى الرئيسي
(د) لمعرفة عدد المدارات التي بداخل كل مستوى فرعي
( )4أعلى عدد إلكترونات تملئ بها المدار الواحد هو:
(ج) 3 e
(ب) 2 e
(أ) 1 e
( )5طاقة مستويات الكم الرئيسية:
(أ) تزداد كلما بعدنا المستويات عن النواه
(ج) متساوية حول النواه
(د) 4 e
(ب) تزداد كلما أقتربت المستويات من النواه
(د) اإلجابات الثالثة خطأ
16.
( )6أعداد الكم األربعة لإللكترون الخامس في عنصر الصوديوم:(أ)
l = 1 , ml = +1 or 0 or -1 , ms = + or – 0.5
n=2
,
(ب) , l = 0 , ml = +1 or 0 or -1 , ms = + or – 0.5
n=3
(ج)
l = 1 , ml = +1 or 0 or -1 , ms = + or – 0.5
,
n=1
(د)
l = 0 , ml = +1 or 0 or -1 , ms = + or – 0.5
,
n=2
( )7أرقام األربعة آلخر إلكترون في عنصر Alهي:
أ ـ l = 0 , ml = 0 , ms = +1/2
n = 1,
ب ـ l = 1 , ml = 1 , ms = +1/2
ج ـ n = 3, l = 1 , ml = -1 , ms = +1/2
د ـ n = 3, l = 2 , ml = -1 , ms = +1/2
n = 2,
17.
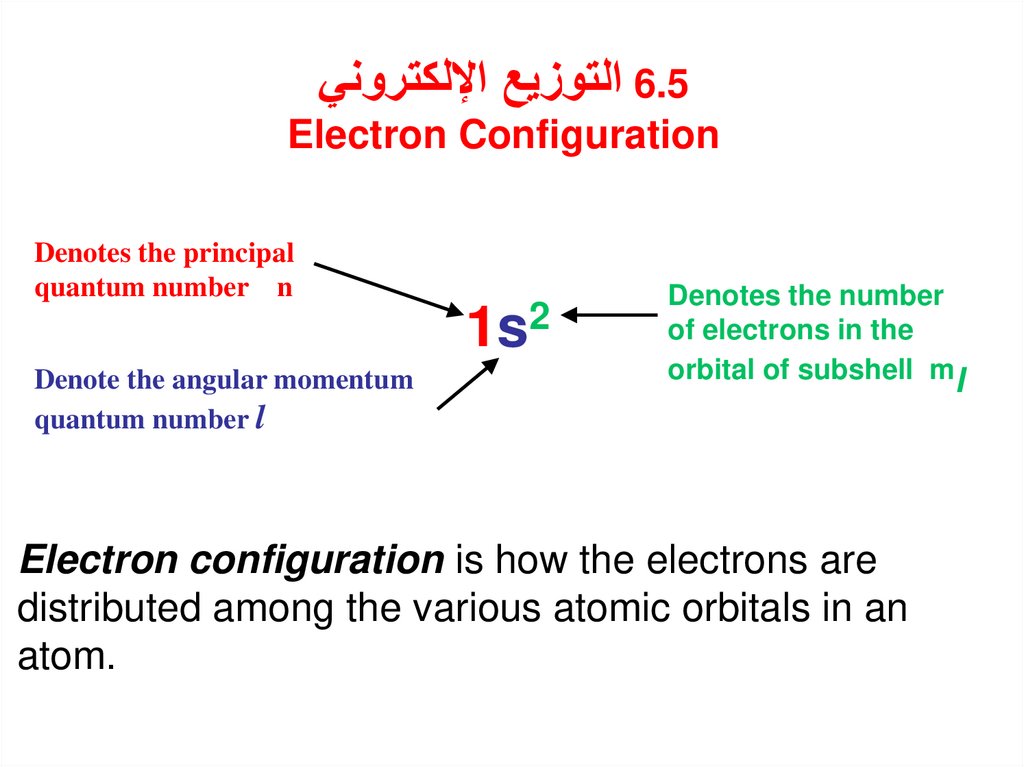
التوزيع اإللكتروني6.5Electron Configuration
Denotes the principal
quantum number n
Denote the angular momentum
quantum number l
1s2
Denotes the number
of electrons in the
orbital of subshell ml
Electron configuration is how the electrons are
distributed among the various atomic orbitals in an
atom.
18.
6d7P
5d
6P
4d
5P
3d
4P
Q (7)
4f
7S
6S
P (6)
5S
O (5)
4S
N (4)
3P
3S
M (3)
الطاقة
تــــزداد
2P
2S
L (2)
1S
K (1)
19.
) (Aمبدأ البناء التصاعديPauli Exclusion Principle :الا وبذلك يمكن
ال بد لإللكترونات أن تشغل مستويات الطاقة الفرعية ذات الطاقة األقل أو ً
ترتيب المستويات الفرعية تصاعديًا ا حسب زيادة طاقاتها كاآلتي.
Order of orbitals (filling) in multi-electron atom
K n=1
L n=2
M n=3
N n=4
O n=5
P n=6
Q n=7
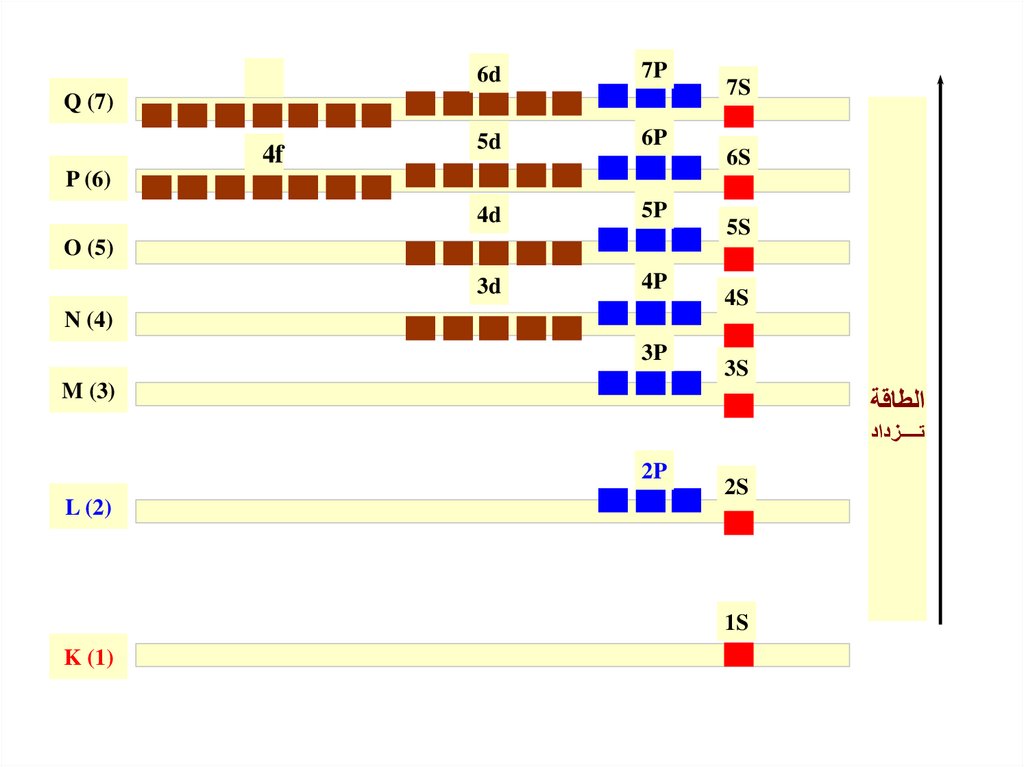
والشكل يوضح طريقة ملء مستويات الطاقة الفرعية تبعًا ا التجاهات األسهم.
1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s
20.
“Fill up” electrons in lowest energy orbitals (Aufbau principle)??
C 6 electrons
B 1s22s22p2
B 5 electrons B 1s22s22p1
Be 4 electrons Be 1s22s2
Li 3 electrons Li 1s22s1
He 2 electrons He 1s2
H 1 electron He 1s2
H 1s1












 physics
physics


