Системы счисления

1. Системы счисления

2.

Системой счисления называется
совокупность правил наименования и
изображения чисел с помощью
конечного набора символов,
называемых цифрами

3.

Система счисления называется
непозиционной, если значение
цифры в записи числа не зависит
от позиции, которую она занимает в
последовательности цифр,
изображающей число.

4.

5.

6.

7.

8.

Система счисления называется
позиционной, если значение цифры
в записи числа зависит от
позиции, которую она занимает в
последовательности цифр,
изображающей число

9.

10.

11.

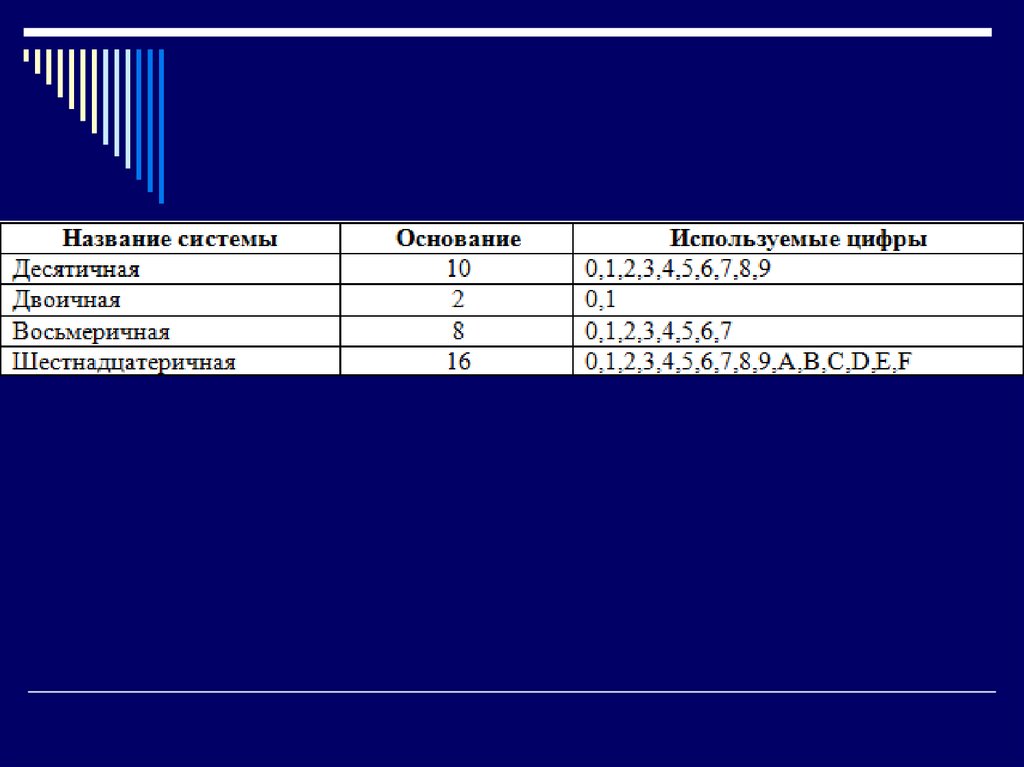
В позиционных системах счисления
основание системы счисления – это
количество цифр, используемых в
записи числа

12.

13.

14. Развернутая форма записи чисел

15. Свернутая форма записи числа

16.

Перевод из десятичной системы
в другие системы счисления

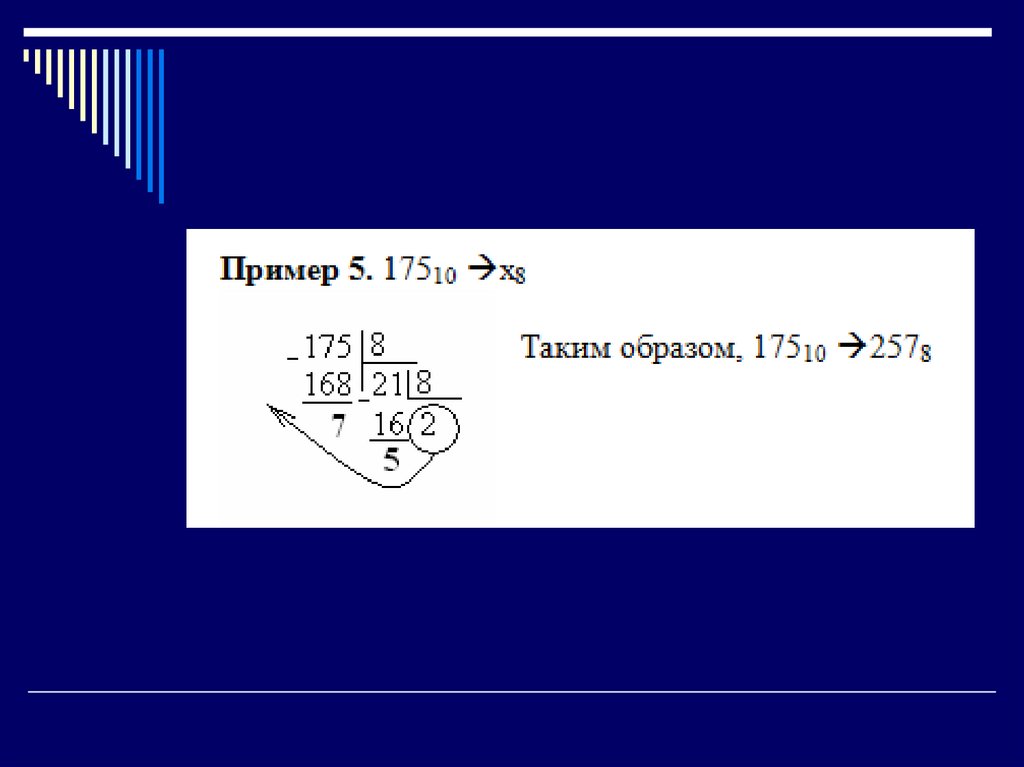
17. Алгоритм перевода целых чисел из десятичной системы счисления в любую другую:

1. Последовательно выполнять деление
данного числа и получаемых целых частных
на основание новой системы счисления до
тех пор, пока не получится частное, меньше
делителя.
2. Полученные остатки, являющиеся
цифрами числа в новой системе счисления, ,
привести в соответствие с алфавитом новой
системы счисления.
3. Составить число в новой системе
счисления, записывая его, начиная с
последнего частного.

18.

19.

20.

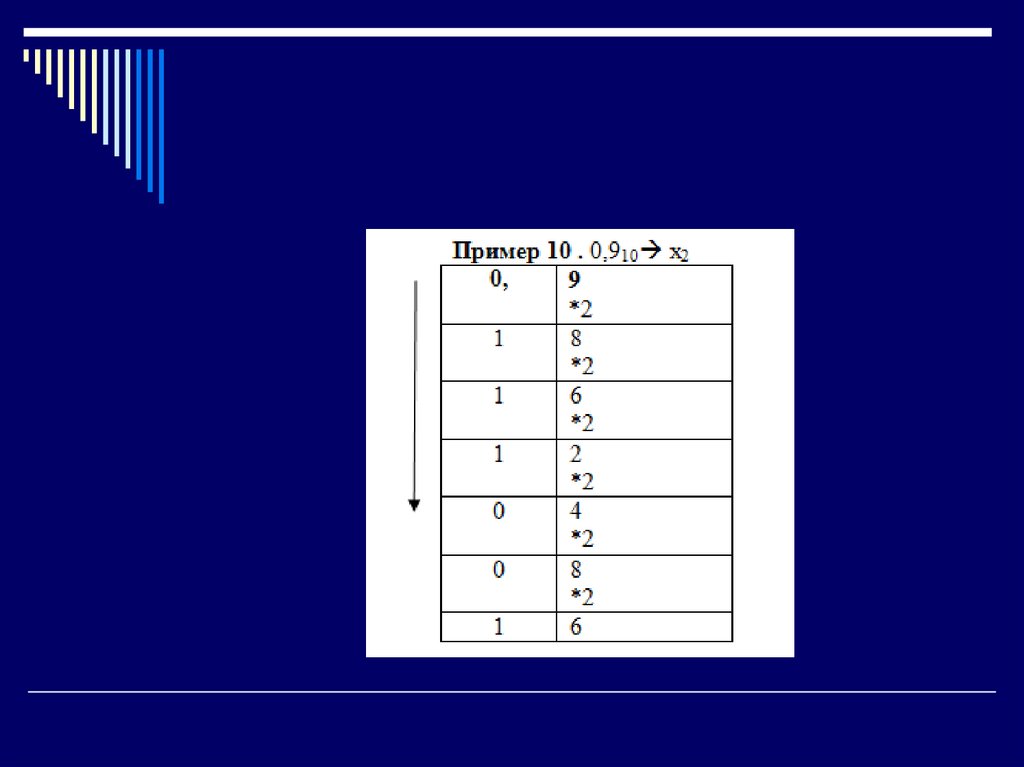
21. Дробную часть числа, если таковая имеется, переводят по другому алгоритму:

1. Последовательно умножить данное число и
получаемые дробные части произведения на
основание новой системы счисления до тех пор, пока
дробная часть произведения не станет равна нулю
или не будет достигнута требуемая точность
представления числа.
2. Полученные целые части произведений,
являющиеся цифрами числа в новой системе
счисления, привести в соответствие с алфавитом
новой системы счисления.
3. Составить дробную часть числа в новой системе
счисления, начиная с целой части первого
произведения.

22.

23.

24.

25.

26.

27.

28.

Перевод чисел из любой
системы счисления в
десятичную

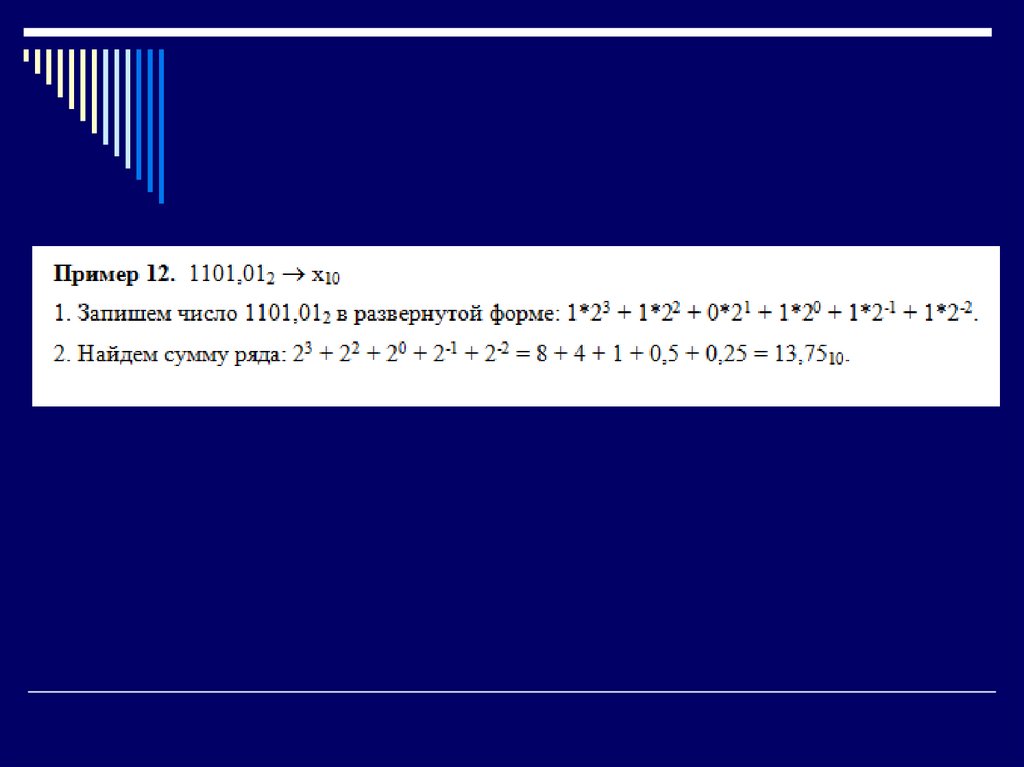
29. Алгоритм перевода чисел из любой системы счисления в десятичную:

1. Представить число в развернутой
записи. При этом основание системы
счисления должно быть представлено
в десятичной системе счисления.
2. Найти сумму ряда. Полученное
число является значением числа в
десятичной системе счисления.

30.

31.

32.

Перевод чисел из двоичной системы
счисления в систему счисления с
основанием
q = 2^n.

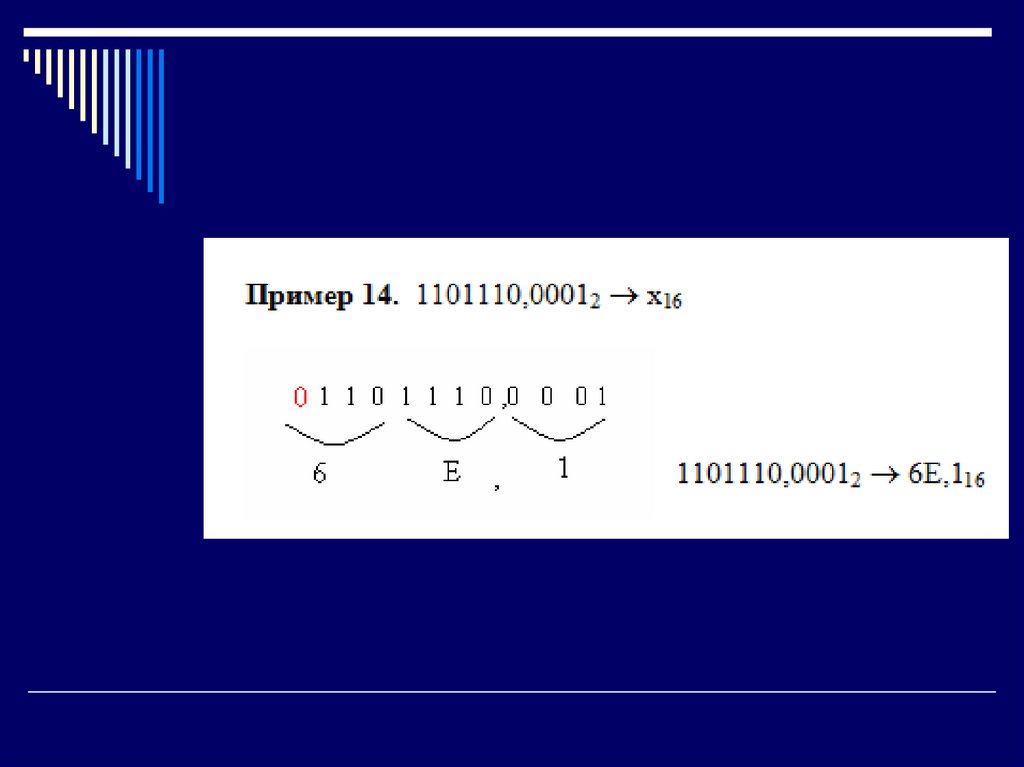
33. Алгоритм перевода двоичных чисел в систему счисления с основанием q = 2^n

1. Целую часть двоичного числа разбить
справа налево, а дробную - слева направо
на группы по n цифр в каждой.
2. Если в крайней левой в целой части и/или
в крайней правой в дробной части группе
окажется меньше n разрядов, то их надо
дополнить нулями до нужного числа
разрядов.
3. Рассмотреть каждую группу как nразрядное двоичное число и записать ее
соответствующей цифрой в системе
счисления с основанием =2^n.

34.

35.

36.

Перевод чисел из системы
счисления с основанием q = 2^n в
двоичную систему счисления

37. Алгоритм перевода чисел из системы счисления с основанием q = 2^n в двоичную систему счисления

1. Каждую цифру числа, записанного в
системе счисления с основанием q =
2^n, заменить ее n-разрядным
эквивалентом в двоичной системе
счисления

38.

39.

40.

Двоичная арифметика

41. Таблица сложения двоичных чисел

42. Таблица вычитания двоичных чисел

43. Таблица умножения двоичных чисел