Similar presentations:
Поведение контура с током в магнитном поле. Лекция 3
1.
ПОВЕДЕНИЕКОНТУРА С ТОКОМ В
МАГНИТНОМ ПОЛЕ
2.
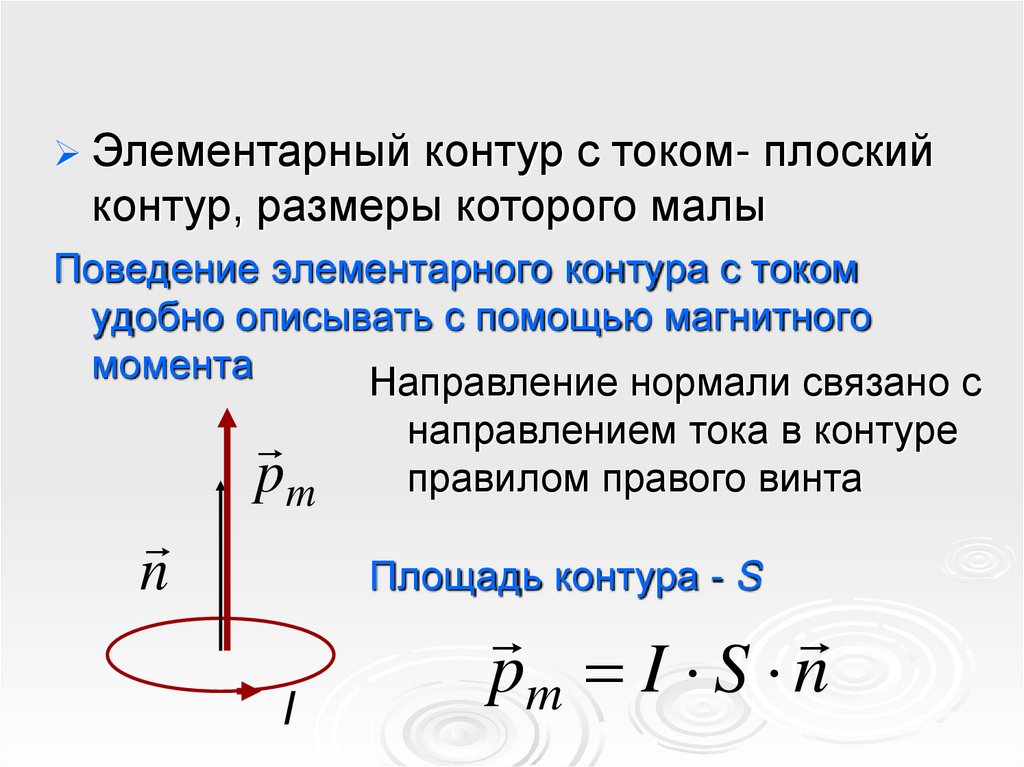
Элементарный контур с током- плоскийконтур, размеры которого малы
Поведение элементарного контура с током
удобно описывать с помощью магнитного
момента
Направление нормали связано с
n
pm
направлением тока в контуре
правилом правого винта
Площадь контура - S
I
pm I S n
3.
Магнитныйpm
момент
Вектор, направлен по нормали к
контуру
Модуль вектора
pm IS
pm А м
2
4.
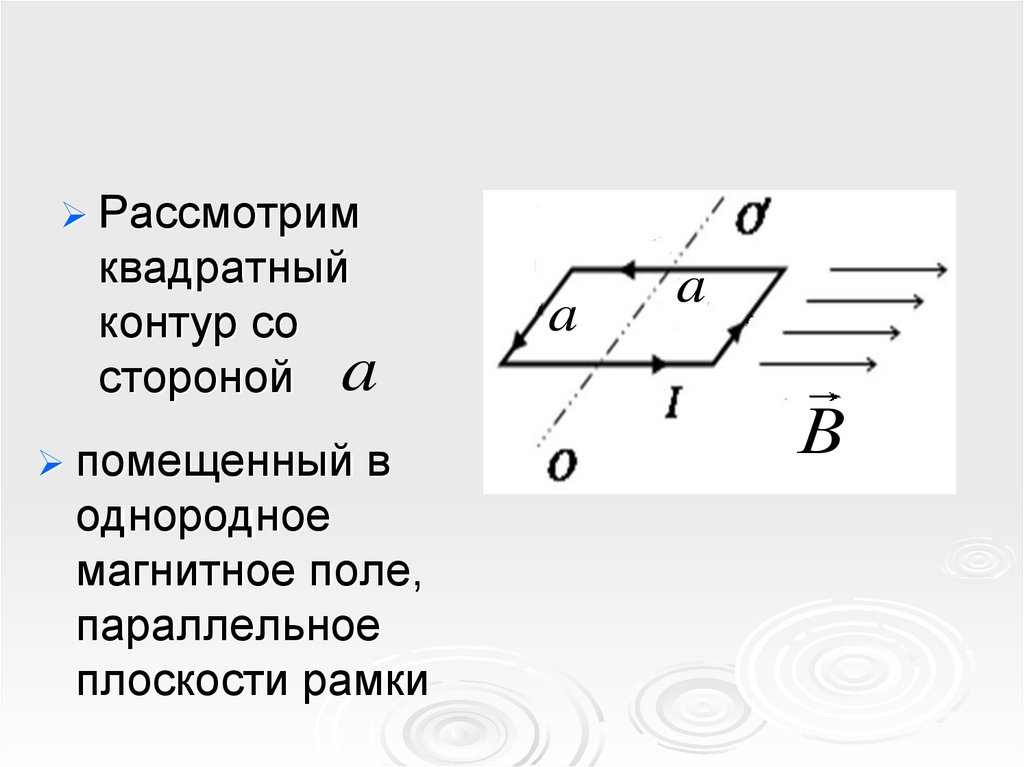
Рассмотримквадратный
контур со
стороной a
помещенный в
однородное
магнитное поле,
параллельное
плоскости рамки
a
a
В
5.
,На проводник с
током,
dF I d B
помещенный в
магнитное поле
действует сила
dF I d B sin(d , B )
Ампера
d
Направлен по току
6.
dF I d BА
d
В
sin(d , B) 0
d
D
Для сторон АВ и CD
C
В
Поэтому сила
Ампера на них не
действует
7.
dF I d BF2
А
D
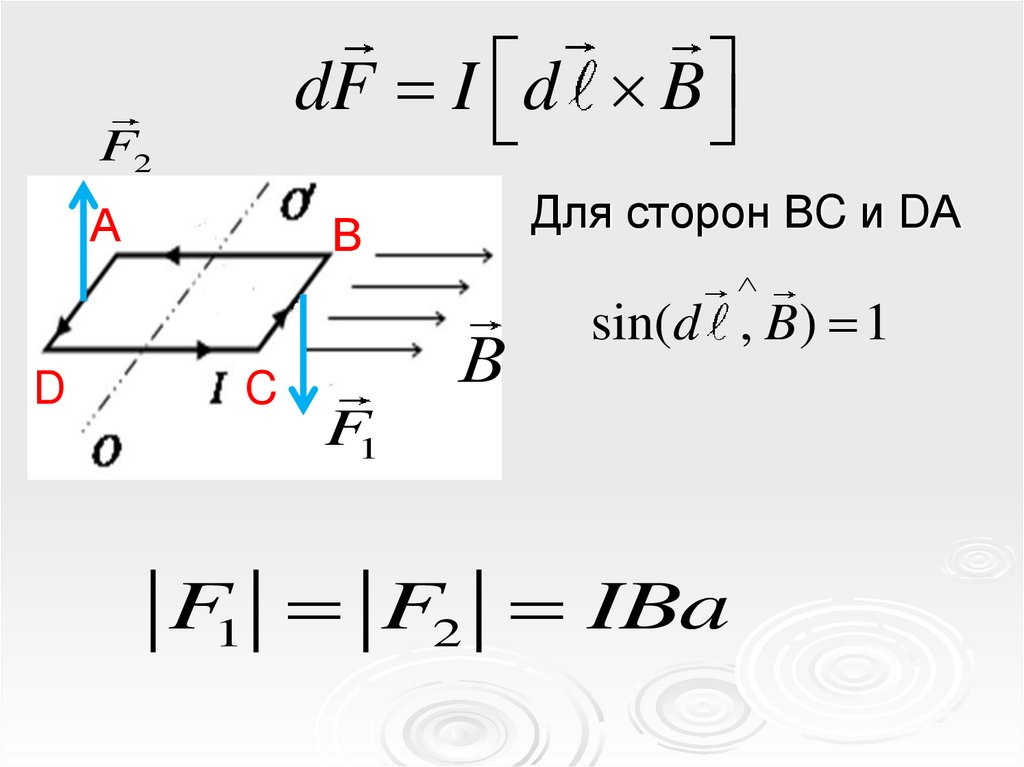
Для сторон ВC и DА
В
C
В
sin(d , B) 1
F1
F1 F2 IBa
8.
rr
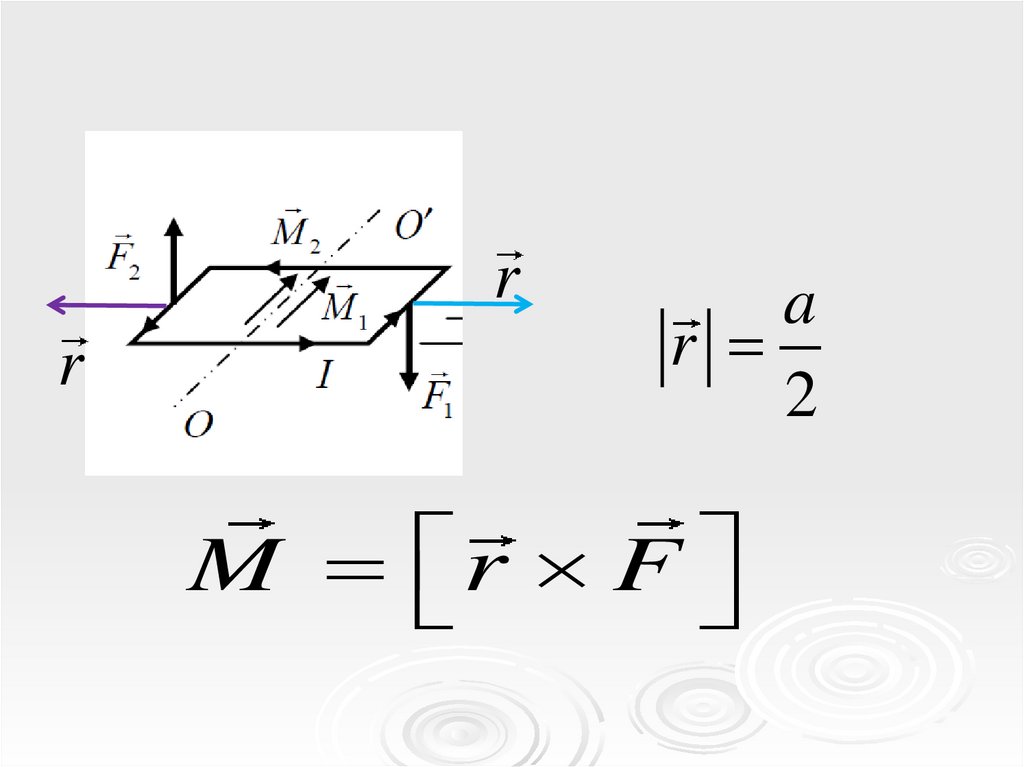
a
r
2
M
r
F
9.
M1 M 2a
IBa
F1
2
2
M M1 M 2 IBa 2
IBS pm B
Pm IS
2
10.
На элементарныйконтур, помещенный в
магнитное поле,
действует момент сил
M
p
B
m
M pm B sin( pm , B)
11.
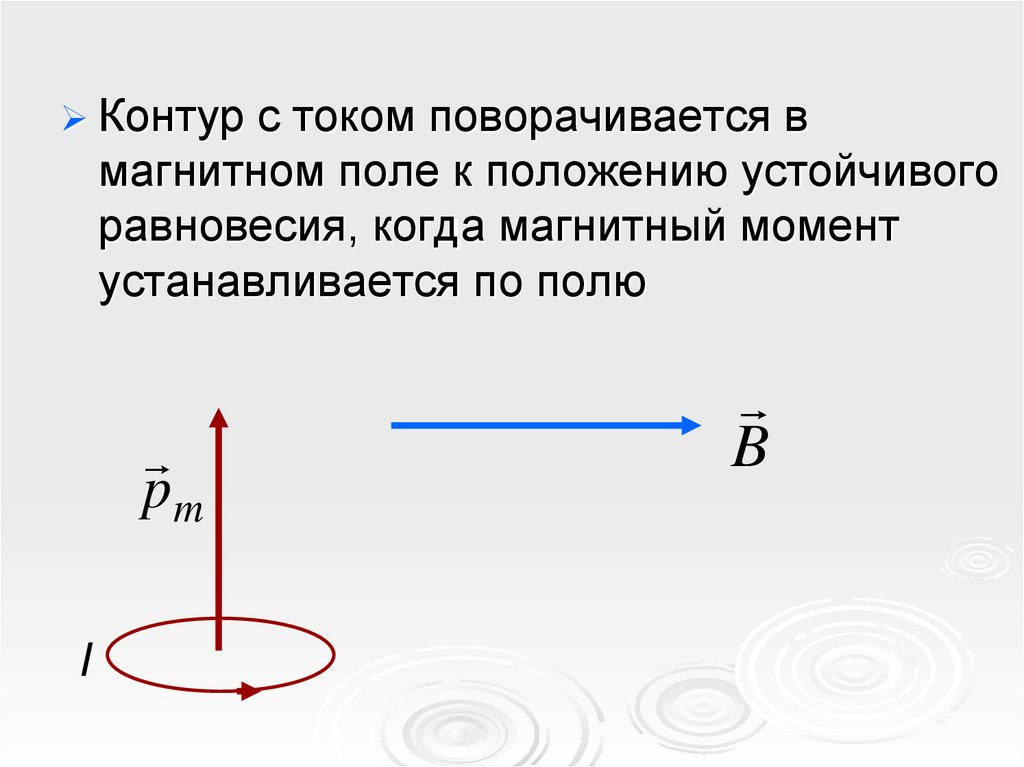
Контур с током поворачивается вмагнитном поле к положению устойчивого
равновесия, когда магнитный момент
устанавливается по полю
pm
I
B
12.
Работа по перемещениюпроводника с током в
магнитном поле
13.
BI
F
На подвижную перемычку действует
сила Ампера
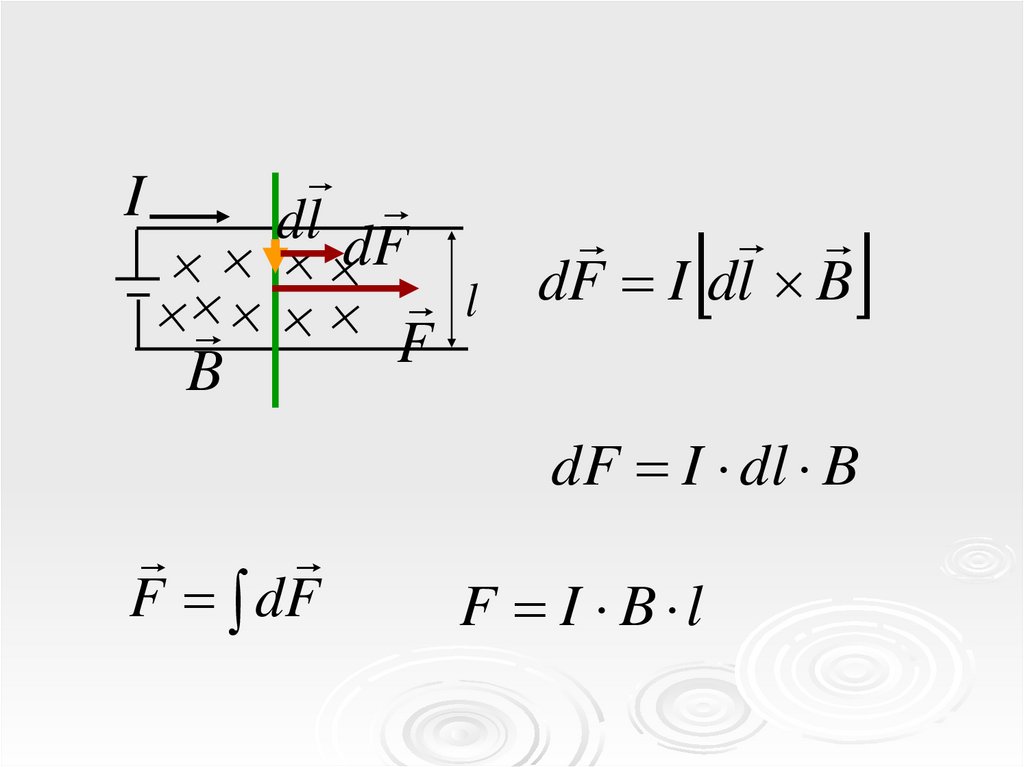
14.
dl dFI
B
l
F
dF I dl B
dF I dl B
F dF
F I B l
15.
При перемещении перемычки сила Амперасовершает работу
I
dS
B
F
dA ( F dx )
F dx 1
dx
I B l dx
площадь, пересекаемая проводником,
l dx dS -при
его движении в магнитном поле
dA I B dS
- поток вектора магнитной индукции
B dS d через эту площадь
dA I d
16.
Работа по перемещению проводника стоком в магнитном поле равна
произведению силы тока на поток
вектора магнитной индукции,
пересекаемый движущимся
проводником
17.
Работа поперемещению
контура с током в
магнитном поле
18.
Рассмотрим прямоугольный контур с током,плоскость которого перпендикулярна линиям
магнитной индукции
2
I
1
3
1
B
2
4
3́
2́
1́ ́
4́
A A12 1 2 A23 2 3 A34 3 4 A41 4 1
A23 2 3 A41 4 1 0 A34 3 4 I ( 2 )
A12 1 2 I ( 1 )
A I ( 1 ) I ( 2 ) I ( 2 1 )
19.
Если ток в контуре постоянен, то работа поперемещению проводника с током
A I ( 2 1 )
Где Ф2 – поток магнитной индукции через
контур в конечном состоянии, Ф1 – поток
магнитной индукции через контур в
начальном состоянии.
Полученное соотношение справедливо для
контуров произвольной формы
20.
Если контурdA I d
неподвижен, а
меняется вектор
магнитной индукции,
то работа
где dФ – изменение
рассчитывается по
магнитного потока
формуле
21.
Законэлектромагнитной
индукции
22.
1831 Майкл Фарадей23.
Закон электромагнитнойиндукции
Какова бы ни была
причина изменения
магнитного потока,
охватываемого
замкнутым
проводящим
контуром,
возникающая в
контуре э.д.с.,
определяется
формулой
d
i
dt
24.
Правило ЛенцаИндукционный ток в контуре всегда имеет
такое направление, что создаваемое им
магнитное поле, препятствует изменению
магнитного потока, вызвавшего этот ток
Следствие закона сохранения энергии
25.
BiB
Ii
B
26.
di
dt
B S BS cos B , n
3 причины изменения
магнитного потока:
1. Изменение магнитного поля
dB
dt
2. Изменение площади S (деформация
контура или движение проводника с током)
3. Изменение угла между магнитным полем и
нормалью (вращение контура в магнитном
поле)
27.
ЭДС индукции в движущемсяпроводнике
Fл e V B
28.
Работа силыЛоренца на пути ℓ
равна
A ( Fл )
Fл eVB
По определению
ЭДС
A
eVB
VB
e
e
29.
Еслисопротивление
всей цепи равно
iинд
R, то по ней
R
будет протекать
индукционный
ток
За время Δt на
сопротивлении
2 2 2
V
B
2
R выделится
Q Riинд t
t
R
джоулево тепло
30.
Причина возникновения эдсиндукции в движущемся
проводнике – сила Лоренца
31.
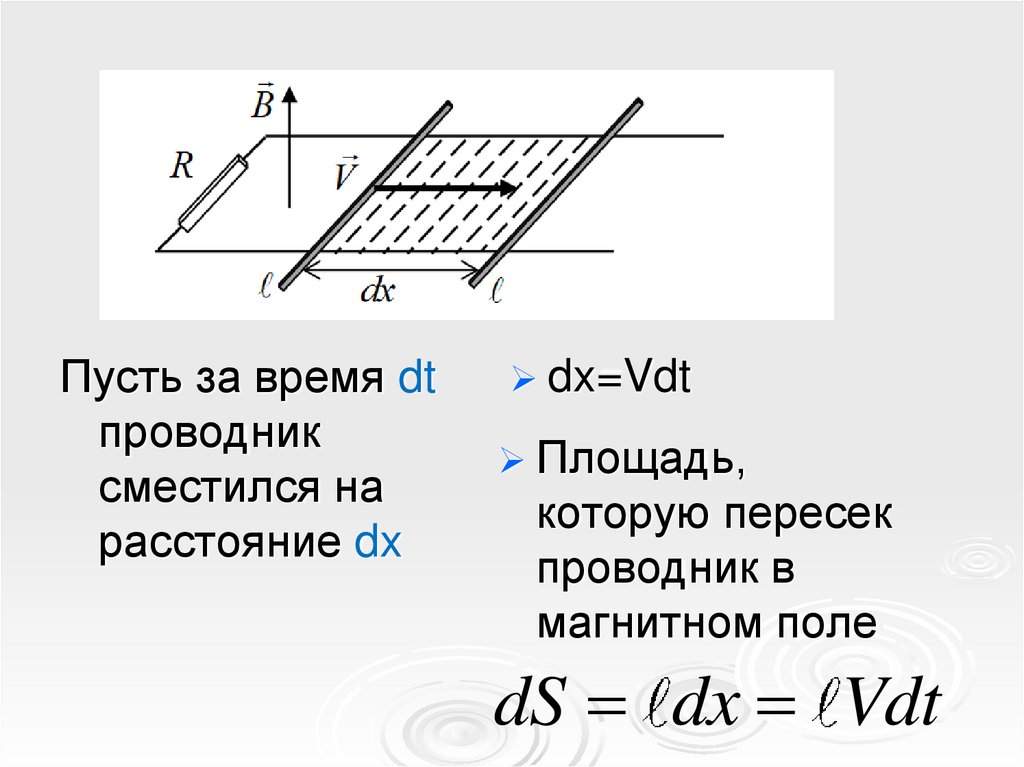
Пусть за время dtпроводник
сместился на
расстояние dx
dx=Vdt
Площадь,
которую пересек
проводник в
магнитном поле
dS dx Vdt
32.
Пересеченныймагнитный поток
d BdS B Vdt
Эдс индукции
d B Vdt
εi
B V
dt
dt
33.
ВРАЩЕНИЕ РАМКИ СТОКОМ В МАГНИТНОМ
ПОЛЕ
34.
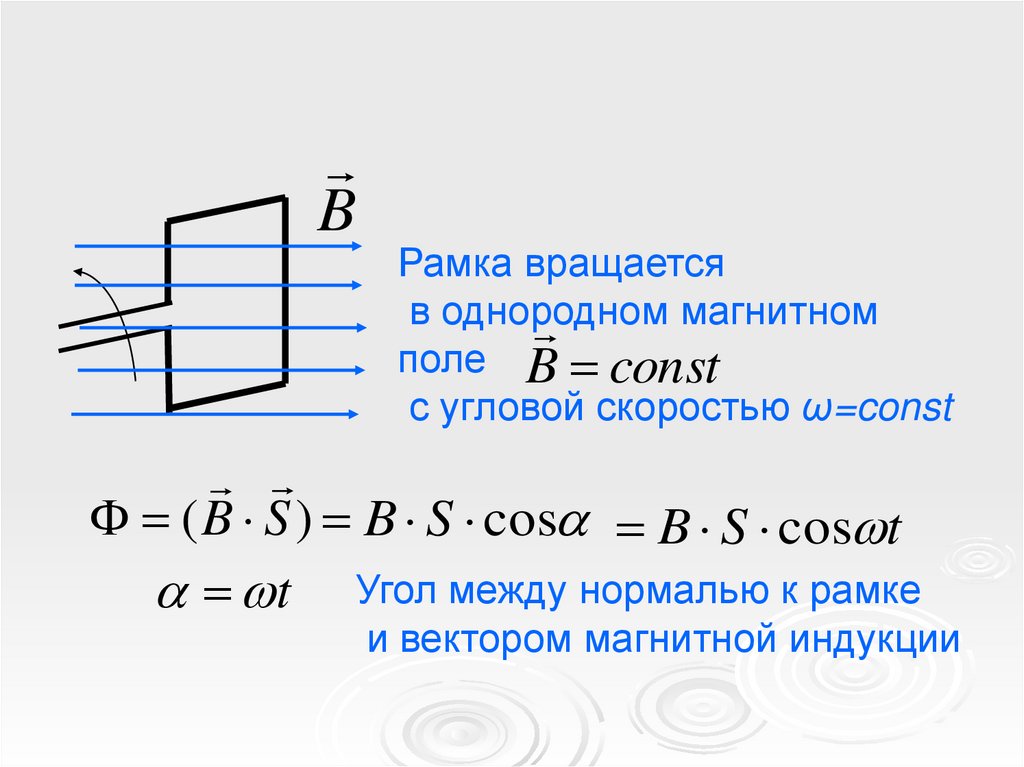
BРамка вращается
в однородном
магнитном
поле B const
с угловой скоростью ω=const
( B S ) B S cos B S cos t
t Угол между нормалью к рамке
и вектором магнитной индукции
35.
При вращении рамки в ней будетвозникать переменная э.д.с. индукции
d
d ( BS cos t )
i
BS
sin
t
dt
dt
sin t 1 , i max BS
i max sin t
36.
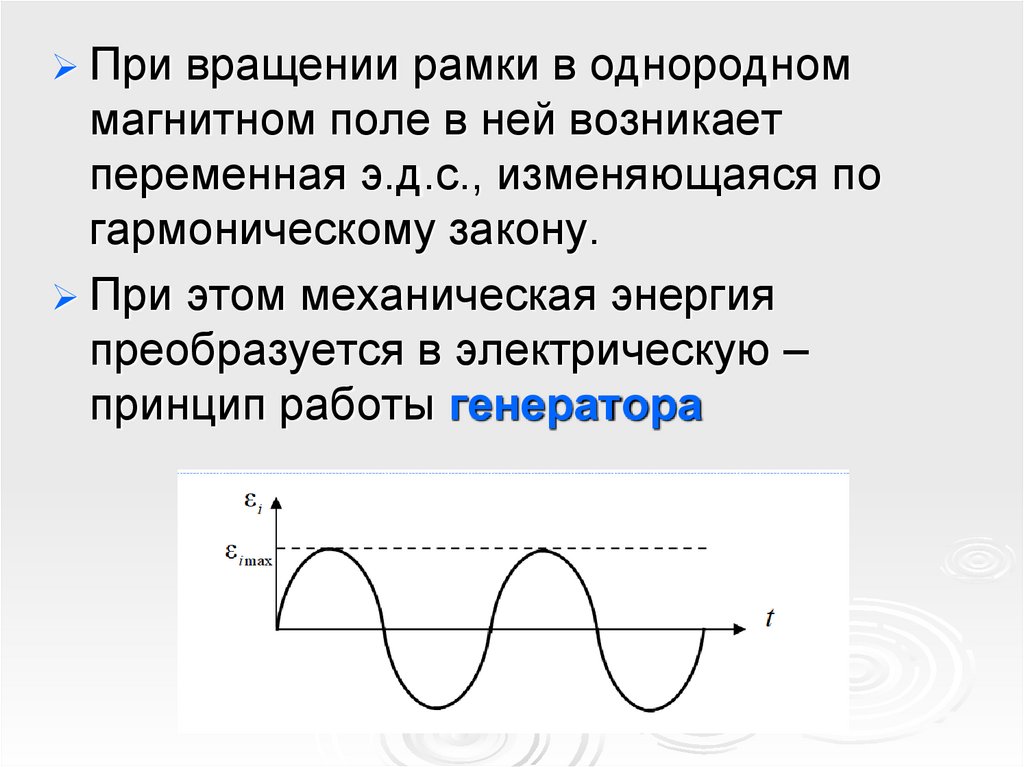
При вращении рамки в однородноммагнитном поле в ней возникает
переменная э.д.с., изменяющаяся по
гармоническому закону.
При этом механическая энергия
преобразуется в электрическую –
принцип работы генератора




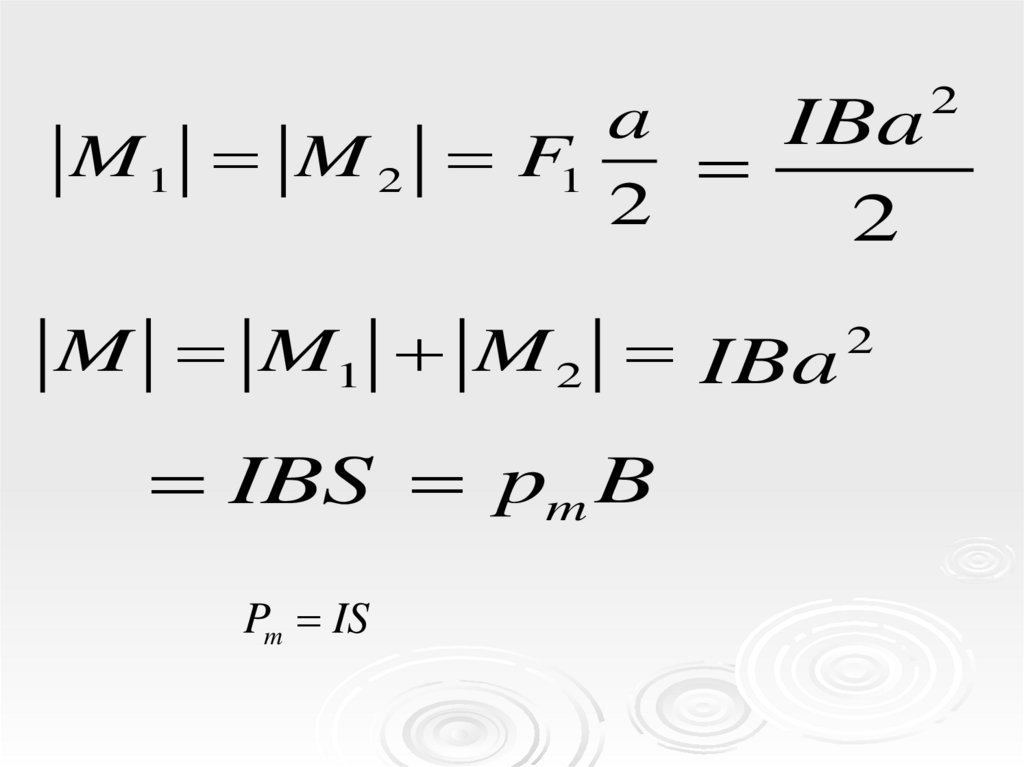





















 physics
physics








