Виды математических моделей

1.

Б1.В.20
МОДЕЛИРОВАНИЕ ПРОЦЕССОВ И СИСТЕМ
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Институт Космических и информационных технологий
Направление 09.03.02. «Информационные
системы и технологии»
Раздел 4. Тема 1 ЛЕКЦИЯ 10 (23.11.2022)
Красноярск 2022

2.

Нельзя запереть ветер.
Застоявшийся ветер
становится спёртым
воздухом!
Точный прогноз погоды
на завтра вы узнаете
послезавтра…

3.

ВИДЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ:
- ЭМПИРИКО-СТОХАСТИЧЕСКИЕ;
-
АНАЛИТИЧЕСКИЕ;
-
САМООРГАНИЗУЮЩИЕСЯ
(ОПТИМИЗИЦИОННЫЕ);
-
ИМИТАЦИОННЫЕ.

4.

Общие проблемы, связанные с
моделированием процессов и
систем:
1. проблема приведения к реальным
масштабам (системы, объекта, процесса);
2. проблема ограничения размерности
системы;
3. проблема параметризации процессов;
4. проблема оценки адекватности модели
в сравнении с реальностью.

5.

ИНТЕРПОЛЯЦИЯ И ЭКСТРАПОЛЯЦИЯ
МОДЕЛИ - операции вероятностного
поиска неизвестных величин,
текстовых смыслов, данных,
значений и т.п
нахождение неизвестной
величины происходит по
ряду известных соседних
величин
(в ряду статистических
данных, И (ИЛИ)
изменяющихся значений).

6.

Типы, виды математических моделей
ДЕТЕРМИНИРОВАННЫЕ (координаты ЭЙЛЕРА)
–
ВЕРОЯТНОСТНЫЕ (координаты ЛАГРАНЖА);
СТАТИЧЕСКИЕ (не учитывают изменения во времени) –
ДИНАМИЧЕСКИЕ (вводится шаг по времени);
ДИСКРЕТНЫЕ (конечное число известных значений)
НЕПРЕРЫВНЫЕ (множество сколь угодно близких друг к другу
значений);
ИНТЕРВАЛ ВРЕМЕНИ ОГРАНИЧЕН –
ИНТЕРВАЛ ВРЕМЕНИ НЕОГРАНИЧЕН (АСИМПТОТИЧЕСКИЕ);
КООРДИНАТНЫЕ –
БЕСКООРДИНАТНЫЕ (0-мерные);
С УПРАВЛЕНИЕМ (настройка испытания) -
БЕЗ УПРАВЛЕНИЯ;

7.

ТИПЫ И ВИДЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
Модель - детерминированная, если каждому входному набору
параметров соответствует вполне определенный и однозначно
определяемый набор выходных параметров; в противном случае –
модель недетерминированная, стохастическая (вероятностная).
Модель – координатная, если для входных параметров Xi заданы
определенные пространственные координаты местоположения
расчетной точки.
Модель - имитационная, если она предназначена для
испытания или управления, проигрывания возможных
путей развития и поведения объекта путем варьирования
некоторых или всех Хi параметров модели.

8.

Модель называется статической, если среди входных
параметров Xi нет временного параметра t. Статическая модель в
каждый момент времени дает лишь "фотографию" системы, ее
срез.
Модель - динамическая, если среди входных параметров Хi есть
временной параметр t, т.е. она отображает систему (процессы в
системе) во времени.
Модель - дискретная, если она описывает поведение системы
только в дискретные моменты (отрезки) времени.
Модель - непрерывная, если она описывает поведение системы
для всех моментов времени из некоторого промежутка времени.

9.

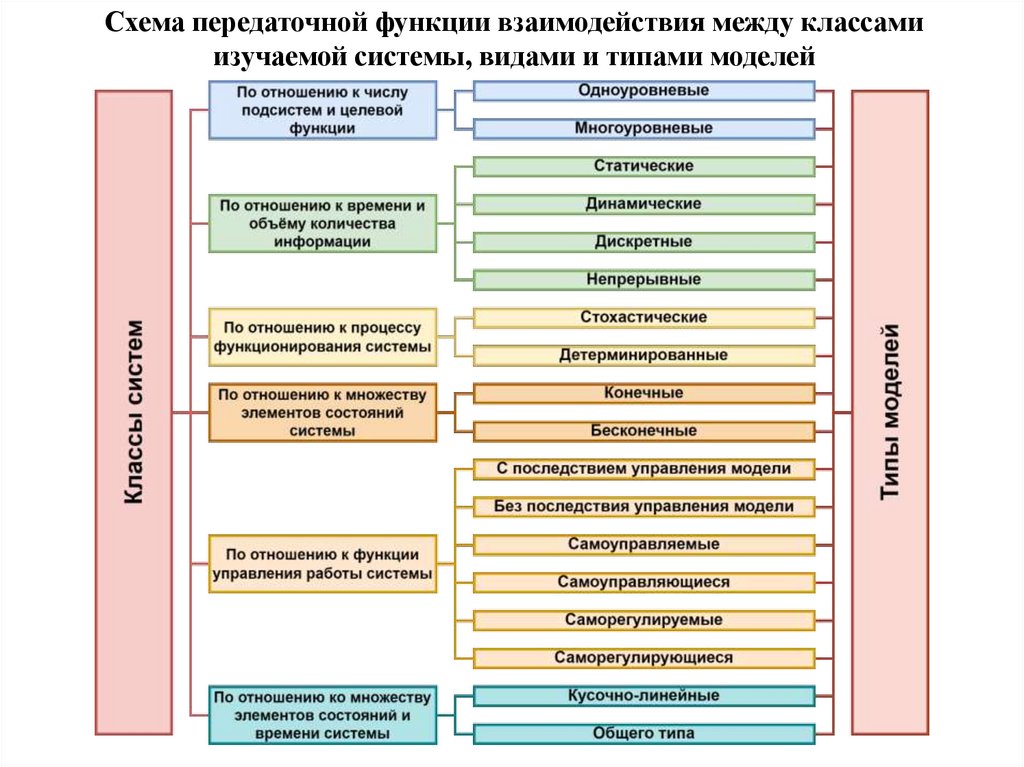
Схема передаточной функции взаимодействия между классами
изучаемой системы, видами и типами моделей

10.

АНАЛИЗ РАЗМЕРНОСТЕЙ (физических)
– ТЕОРИЯ ПОДОБИЯ
- АНАЛИТИЧЕСКИЕ МОДЕЛИ
-
ФИЗИЧЕСКОЕ МОДЕЛИРОВАНИЕ
- ПАРАМЕТРИЗАЦИЯ
1-я теорема теории размерностей:
Вторичные физические величины можно выразить через комплекс
первичных в виде многочлена, и можно найти функциональную
зависимость используя определенные факты, при
этом размерность любой физической величины имеет степенной
вид
y x x x ... x
K1
1
K2
2
K3
3
n
Kn

11.

-теорема теории подобия
Всякая зависимость между (n+1)
размерными величинами, из
имеют независимую размерность,
которых
r n
может быть представлена или
сведена к зависимости между:
m n 1 r БЕЗРАЗМЕРНЫХ КОМПЛЕКСОВ
a 0 a1 , a 2 ... a r , a r 1 ... a n
a1 , a 2 - независимые размерности; физические
величины, размерности которых не могут
быть выражены через размерность других
величин
a r , a r 1 - размерность можно выразить через a1 , a 2

12.

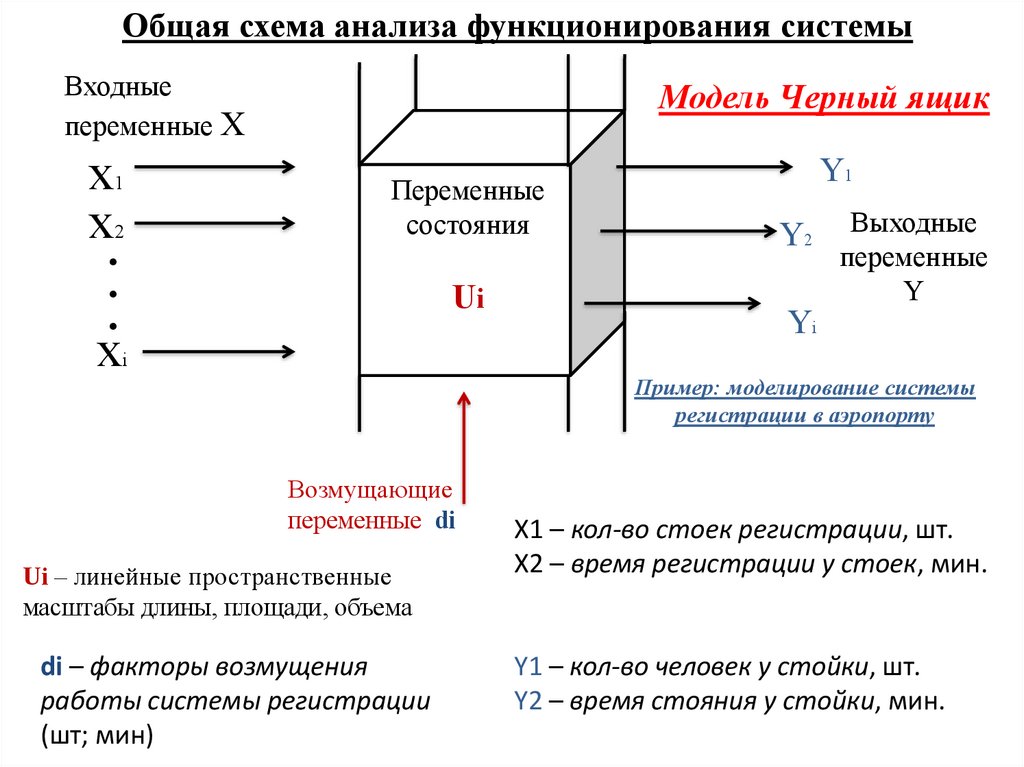
Общая схема анализа функционирования системы
Входные
переменные X
x
x
1
.
.
.
2
Модель Черный ящик
Переменные
состояния
Ui
x
Y1
Y2
Yi
Выходные
переменные
Y
i
Пример: моделирование системы
регистрации в аэропорту
Возмущающие
переменные di
Ui – линейные пространственные
масштабы длины, площади, объема
di – факторы возмущения
работы системы регистрации
(шт; мин)
X1 – кол-во стоек регистрации, шт.
Х2 – время регистрации у стоек, мин.
Y1 – кол-во человек у стойки, шт.
Y2 – время стояния у стойки, мин.

13.

Видовое представление взаимодействия систем для модели
«Черный ящик»
Соприкасающиеся грани геометрических фигур, можно
представить как входные и выходные сигналы систем

14.

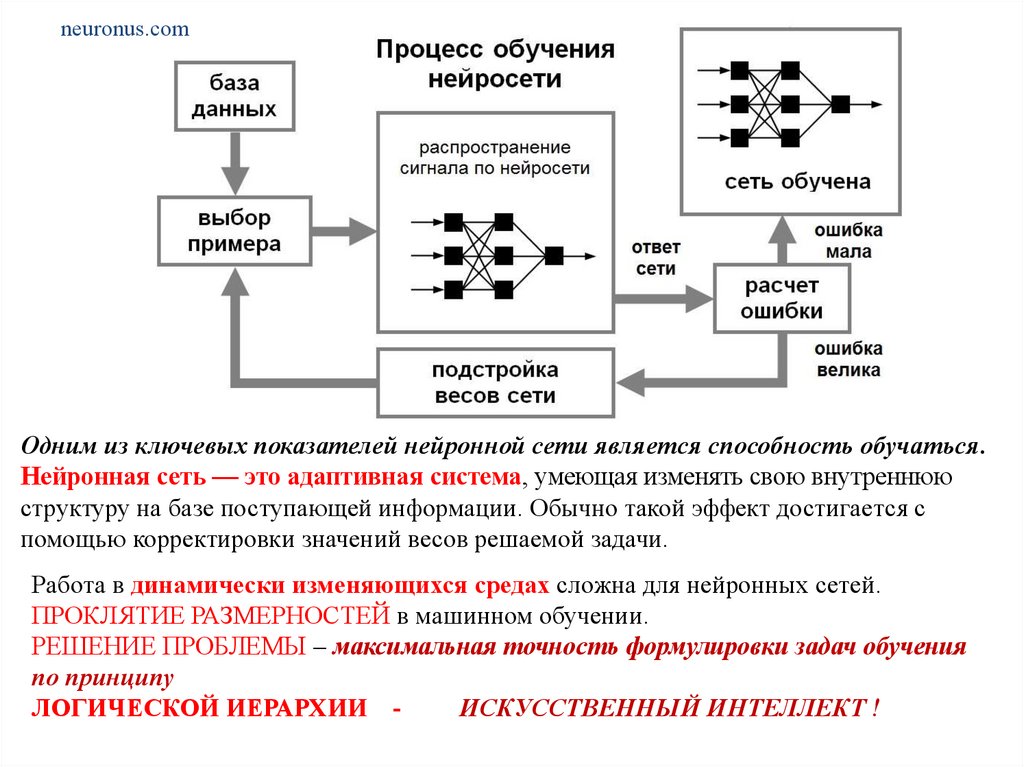
neuronus.com
Одним из ключевых показателей нейронной сети является способность обучаться.
Нейронная сеть — это адаптивная система, умеющая изменять свою внутреннюю
структуру на базе поступающей информации. Обычно такой эффект достигается с
помощью корректировки значений весов решаемой задачи.
Работа в динамически изменяющихся средах сложна для нейронных сетей.
ПРОКЛЯТИЕ РАЗМЕРНОСТЕЙ в машинном обучении.
РЕШЕНИЕ ПРОБЛЕМЫ – максимальная точность формулировки задач обучения
по принципу
ЛОГИЧЕСКОЙ ИЕРАРХИИ ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ !

15.

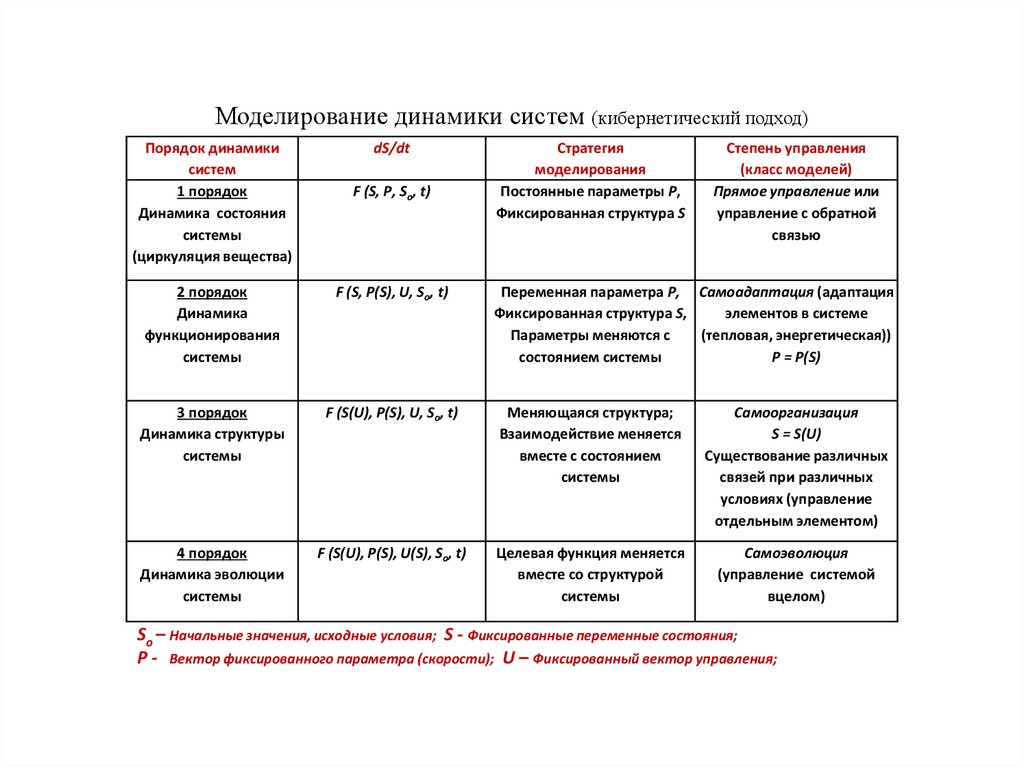
Моделирование динамики систем (кибернетический подход)
Порядок динамики
систем
1 порядок
Динамика состояния
системы
(циркуляция вещества)
dS/dt
F (S, P, So, t)
Стратегия
моделирования
Постоянные параметры P,
Фиксированная структура S
Степень управления
(класс моделей)
Прямое управление или
управление с обратной
связью
2 порядок
Динамика
функционирования
системы
F (S, P(S), U, So, t)
Переменная параметра P, Самоадаптация (адаптация
Фиксированная структура S,
элементов в системе
Параметры меняются с
(тепловая, энергетическая))
состоянием системы
P = P(S)
3 порядок
Динамика структуры
системы
F (S(U), P(S), U, So, t)
Меняющаяся структура;
Взаимодействие меняется
вместе с состоянием
системы
Самоорганизация
S = S(U)
Существование различных
связей при различных
условиях (управление
отдельным элементом)
4 порядок
Динамика эволюции
системы
F (S(U), P(S), U(S), So, t)
Целевая функция меняется
вместе со структурой
системы
Самоэволюция
(управление системой
вцелом)
So – Начальные значения, исходные условия; S - Фиксированные переменные состояния;
P - Вектор фиксированного параметра (скорости); U – Фиксированный вектор управления;

16.

МОДЕЛИ УСТРОЙСТВ И СИГНАЛЫ ПАРАМЕТРОВ
Для широкого класса технических устройств модель
функционирования системы может быть представлена как
реакция на входные возмущения и начальное состояние
(входной сигнал).
Реакцию системы будем называть - выходной сигнал.
МОДЕЛЬ «ЧЕРНЫЙ ЯЩИК»
Например:
- для механических устройств, входные сигналы – силы,
моменты, а выходные – скорости, ускорение;
- для радиотехнических и электронных систем, входные
сигналы – токи, напряжения, а выходные – звук,
изображение на мониторе;
-для организационных систем, входные сигналы
проблемы, а выходные сигналы - решение проблем.
–