Метод разметки. Тема 5

1.

Метод разметки
Цель: разработать метод глобального анализа
свойств программ.
План:
1. Ориентированные мультиграфы, как абстракция
управляющей структуры программы
2. Полурешётки, как абстракция понятия «свойство»
3. Метод разметки на графах для нахождения (приближённого)
решения задачи глобального анализа
4. Стандартные схемы, как модель императивных программ.
5. Равенство термальных значений, как анализируемое
свойство
6. Логико-термальная эквивалентность схем программ, для
разрешения которой требуются глобальный анализ.

2.

Ориентированный мультиграф
• Ориентированный мультиграф
Г=(V,E,нач,кон)
– V – множество вершин
– E – множество дуг
– нач : E V { } - начало дуги
– кон : E V { } - конец дуги
где V – символ свободной дуги

3.

Пример
нач
e1
e2
v1
e3
e4
v3
e5
e6
e7
v4
e8
e2
v1
e3
v1
v2
e4
v1
v3
e5
v2
v3
e6
v3
e7
v4
v4
e8
e1
v2
кон
v1
v2

4.

Определения
• Входная дуга e: нач(е) =
• Выходная дуга e: кон(е) =
• Смежные дуги е1, e2:
v V : (v=нач(e1) v=кон(e1)) &
(v=нач(e2) v=кон(e2))
• Окрестность e:
окр(е) = {e’ | e смежна е’}

5.

Определения
• Путь: … vi, ei, vi+1, ei+1, …, такая что
нач(еi) = vi & кон(еi) = vi+1
• Маршрут: e1,…,en, такая что ei смежна ei+1
• Отличия:
– маршрут может быть против направления дуг.
Пример, е1, е2, е2, е1
– машрут конечен
• Обозначение: марш(е1,е2) - множество
маршрутов от e1 к е2.

6.

Полурешётка свойств
• Полурешётка (L, )
– x,y,z L:
x x = x - идемпотентность
x y = y x - коммутативность
(x y) z = x (y z) - ассоциативность
• Частичный порядок:
x,y : x y x y = x
• Наибольший и наименьший элементы:
x:0 x 1
n
• Обозначение.
x1∧ x2∧ ...∧ xn= ∏ xi
i= 1

7.

Полурешётка свойств
• Обрыв цепей: любая строго убывающая
последовательность конечна.
• Ограниченность:
x bx x1,…,xn : ( i : xi>xi+1) n bx
• Пример: L={0 1} – ограниченная.
• Пример: L={0 1} {(i,j) | 1 j i}, где
(i,j) (i’,j’) i=j & i’ j’ – с обрывом цепей,
но не ограниченная.

8.

Пример: с обрывом цепей, но не
ограниченная
1
(1,1)
(2,2)
(3,3)
(4,4)
(2,1)
(3,2)
(4,3)
(3,1)
(4,2)
…
(4,1)
…
0

9.

Бесконечное пересечение
• Лемма. В полурешётке с обрывом цепей для
любой последовательности xi определено
пересечение
∞
x= ∏ xi
i= 0
• Доказательство. Последовательность y0=x0,
yi+1=yi xi+1 монотонно убывает и имеет
конечное число различных элементов.

10.

Преобразователи свойств
• Монотонная функция f : L L
x,y : x y f(x) f(y)
• Утверждение. Функция f монотонна
тогда и только тогда, когда
x,y : f(x y) f(x) f(y) (мен. Инф.
Мен. выход)
• Доказательство. (Упражнение)
• Дистрибутивная функция f : L L
x,y : f(x y) = f(x) f(y)

11.

Задача глобального анализа
1. Граф (V,E,нач,кон)
2. Полурешётка свойств (L, ) со
свойством обрыва цепей
3. Начальная разметка 0 : E L
4. Функция переноса свойств:
f : E E (L L)
для смежных дуг e1 и e2 определяет
монотонную функцию переноса
информации с e1 на e2

12.

Точное решение ЗГА
• Перенос вдоль маршрута =e1,…,en:
g (x) = x, при n=1
g (x) = f(en-1,en)(g '(x)), если = 'en-1,en
т.е.
g f(en-1,en)○… ○f(e2,e3)○f(e1,e2)
• Точное решение ЗГА:
H(e)= ∏
∏
e' ∈ E ω∈ марш(e',e)
gω( μ0 (e' ))

13.

Процесс разметки
• Последовательность разметок: 0, 1,
…., n,…
• 0 = 0
• Правило разметки: выбираем
произвольную пару смежных дуг e1 и e2
i+1(e2) = i(e2) f(e1,e2)( i(e1))
i+1(e) = i(e), при e e2

14.

Стационарная разметка
• Разметка c – стационарна, если она не
изменяется любым применением правила
разметки
• Утверждение. Для любой ЗГА существует
стационарная разметка.
• Доказательство.
– При каждом не «холостом» применении правила
разметки пометка хотя бы одной дуги убывает.
– ЗГА подразумевает свойство обрыва цепей.
• Конец доказательства.

15.

Безопасная разметка
• Разметка безопасна, если
e : (e) H(e)
• Теорема. Любая стационарная
разметка безопасна.
• Доказательство. Требуется показать,
что для любой дуги e
μc (e)≤ H(e)= ∏
∏
e' ∈ E ω∈ марш(e',e)
gω( μ0(e' ))

16.

Доказательство
– Позже покажем, что
∀ S⊆ L:(∀ x∈ S: x≥ y)⇒ ∏ x ≥ y
( )
x∈ S
– То есть достаточно показать, что
∀ e' ∈ E∀ ω∈ марш( e', e): μc( e)≤ gω μ0 e'
– Индукция по длине :
– | |=1) e=e’ и значит g 0e’ = 0e >= ce

17.

Доказательство
= 'e''e)
g 0e' = f(e'',e) g ' 0e' // по определению
f(e'',e) сe'' // по предп. индукции
сe // ввиду стационарности
• Конец доказательства.

18.

Единственность стационарной
разметки
Теорема. Стационарная разметка с
является наибольшим решением системы
уравнений
μe= μe∧
∏ f ( e', e)( μe' )
e' ∈ окр(е)
среди 0
(для кажд дуги зап такое уравнение => сист ур)
Доказательство. Требуется доказать
(A) с – решение
(B) с – наибольшее

19.

Доказательство
(A) с – решение?
1. Дистрибутивность,
идемпотентность
2. Стационарность
3. Идемпотентность
μc e∧
1
∏ f (e' e)( μc e' )=
e' ∈ окр( е)
¿ ∏
e' ∈ окр( е)
¿ ∏
e' ∈ окр( е)
2
(μc e∧ f ( e' e)( μc e' ))=
3
μc e= μc e

20.

Доказательство
(B) с – наибольшее? Пусть - решение.
Поскольку с - достижима, то достаточно
показать
’ : ( ’ – достижима ’).
Индукция по количеству применений
правила разметки:
База: ’ = 0 по условию теоремы

21.

Доказательство
Шаг: Пусть ’ получается из ’’ (для которой уже
доказано) применением правила разметки к
дугам e1 и е2.
’(e) = ’’(e) (e), при при e e2
’(e2) = ’’(e2) f(e1,e2)( ’’(e2)) // монотонность
(e2) f(e1,e2)( (e2))
// – решение
(e2)
Конец доказательства.
Следствие. с– единственна.

22.

Дистрибутивный случай
Теорема. Если все функции переноса
дистрибутивны, то стационарная разметка
с совпадает с H - точным решением ЗГА.
Доказательство. Уже доказано, что с –
безопасна, т.е. с H. Осталось доказать,
что с H. Докажем это индукцией по
количеству применений правила разметки
для всех достижимых разметок

23.

Доказательство
• База индукции: ’ = 0
μ0 (e)≥ H(e)= ∏
∏
e' ∈ E ω∈ марш(e',e)
gω(μ0 (e' ))
поскольку
– e E
– =e марш(e,e)
– g ( 0(e)) = 0(e)
– пересечение 0(e) с g ( 0(e‘)) для остальных e’ и
результат не увеличивает.

24.

Доказательство
• Шаг: Пусть получается из ’ (для которой уже
доказано) применением правила разметки к дугам e’
ие
1
2
μ(e)= μ' (e)∧ f (e', e)( μ' (e' ))¿
3
¿H (e)∧ f (e',e)( H (e' ))=
¿H (e)∧ f (e',e) ∏
∏
(
e'' ∈ E ω∈ марш(e'',e' )
¿H (e)∧ ∏
gω ( μ0 (e'' )) =
)
5
∏
f (e',e)(gω ( μ0 (e'' )))¿
∏
6
e''∈ E ω∈ марш(e'',e' )
¿H (e)∧ ∏
4
e''∈ E ω∈ марш(e'',e)
7
¿H (e)∧ H (e)= H (e)
gω ( μ0(e' ))=

25.

Доказательство
Комментарии:
1. Правило разметки
2. Предположение индукции, монотонность
3. Определение H(e)
4. Дистрибутивность f(e’,e)
5. Подмножество маршрутов: только те, которые
заканчиваются дугой e
6. Определение H(e’)
7. Идемпотентность
Конец доказательства.

26.

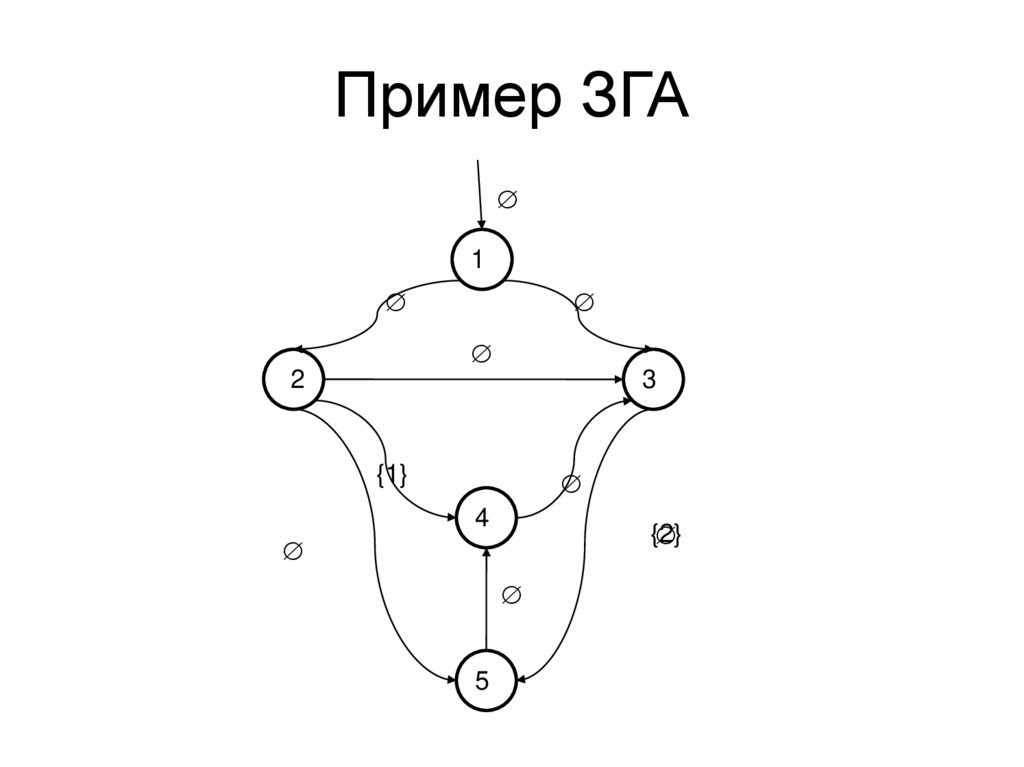
Пример ЗГА
• Задача. Найти все вершины, лежащие
на циклах, т.е. такие v, что
n>0 v1,…,vn : v1=v & vn=v &
( i<n e : нач(е)=vi & кон(е)=vi+1)
• Вспомогательная задача. Для каждой
вершины v найти множество тех
вершин, из которых есть путь в v.

27.

Пример ЗГА
1. Граф Г=(V,E,нач,кон)
пересеч )
2. Полурешётка: (P(V),П
Идемпотентность, коммутативность,
дистрибутивность – очевидны.
– частичный порядок
V – наименьший элемент, –
наибольший
3. Начальная разметка:
0(e) =

28.

Пример ЗГА
4. Функция переноса
f(e1,e2)(S) = S П {нач(e1)},
если нач(e1) & кон(e1)=нач(e2)
f(e1,e2)(S) = , иначе
Дистрибутивность функций переноса:
S1 S2 (S1 П {x}) (S2 П {x})
Формулировка ЗГА завершена.

29.

Пример ЗГА
• Перенос вдоль маршрута e1,…,en
(здесь и далее кон(ei)=нач(ei+1) )
g (S) = f(en-1,en)○… ○f(e2,e3)○f(e1,e2)(S) =
= S {нач(ei) | i=1..n-1}
• Точное решение
H(e)= U
U
e1 e1 ,...,en,e∈ марш(e1,e)
{нач(e)|i= 1..n}
- то, что требуется
• Метод разметки даёт точное решение.

30.

Пример ЗГА
1
2
3
{1}
4
5

31.

Пример ЗГА
1
2
3
{1}
4
{2}
5

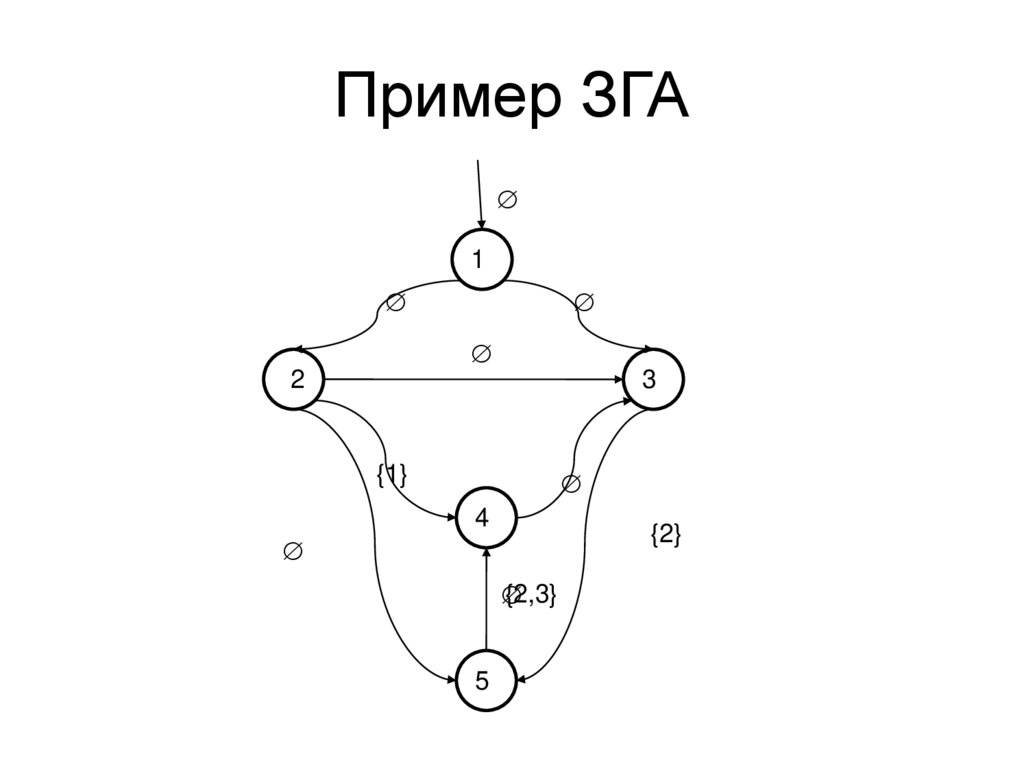
32.

Пример ЗГА
1
2
3
{1}
4
{2}
{2,3}
5

33.

Пример ЗГА
1
2
3
{2,3,5}
{1}
4
{2}
{2,3}
5

34.

Пример ЗГА
1
{1}
2
3
{2,3,5}
{1}
4
{2}
{2,3}
5

35.

Пример ЗГА
1
{1}
2
3
{2,3,5}
{1}
4
{2}
{1}
{2,3}
5

36.

Пример ЗГА
1
{1}
2
3
{2,3,5}
{1}
4
{2}
{1}
{2,3}
{1,2,3}
5

37.

Пример ЗГА
1
{1}
2
3
{1,2,3,5}
{2,3,5}
{1}
4
{2}
{1}
{1,2,3}
5

38.

Пример ЗГА
1
{1}
2
3
{1,2,3,5}
{1}
4
{2}
{1,2,3,4,5}
{1}
{1,2,3}
5

39.

Пример ЗГА
1
{1}
2
3
{1,2,3,5}
{1}
4
{1,2,3,4,5}
{1}
{1,2,3}
{1,2,3,4,5}
5

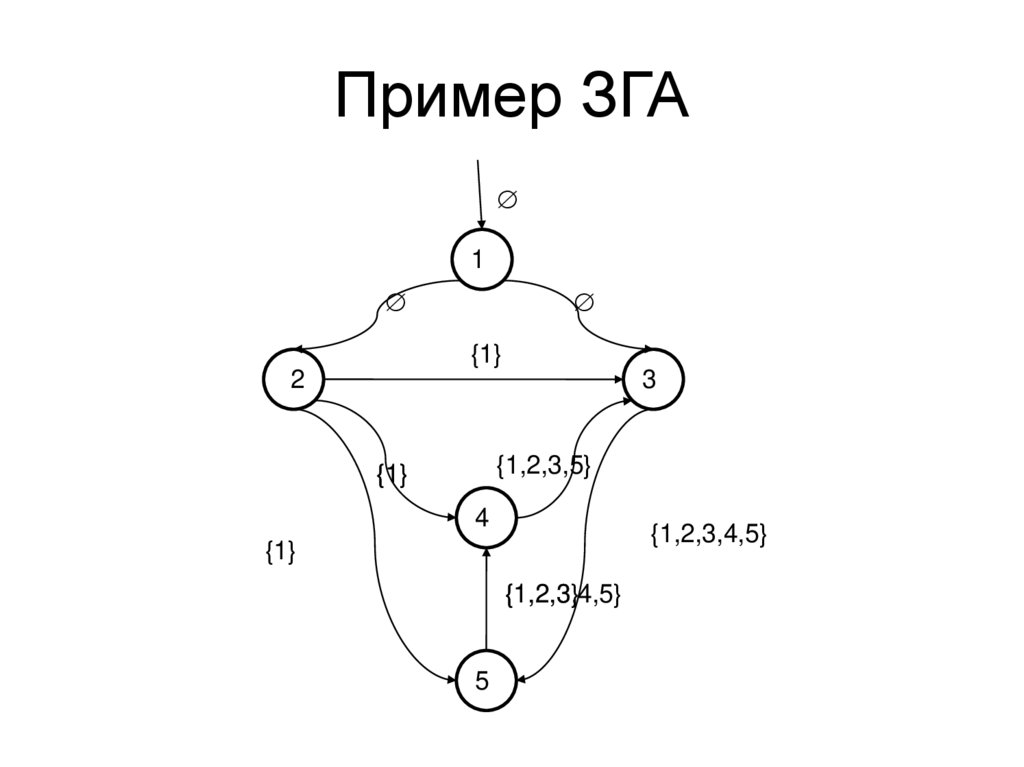
40.

Пример ЗГА
1
{1}
2
3
{1}
{1,2,3,4,5}
{1,2,3,5}
4
{1,2,3,4,5}
{1}
{1,2,3,4,5}
5
Стационарная

41.

Минимизация применений
правила разметки
• Множество активных дуг:
– Правило разметки применяется только для
e1 и e2, где e1 – активна.
– Если справдливо, что для всех функций
f(1)=1, то в начальный момент активны
только e, такие, что 0(e) 1
– Дуга становится активной, если меняется
её пометка
• Учёт структурных свойств графа?

42.

Невозможность построения
точного решения
• Теорема. Если функции пронесения
монотонны, то не существует алгоритма,
который для любой ЗГА находил бы точное
решение.
• Доказательство. Сведение к (неразрешимой)
проблеме Поста:
– Дано: A=( 1,…, n), B=( 1,…, n), i, i X*
– Найти: i1,…,ik, k>0, такую что
α i ...α i k = βi 1 ... βi k
1
(Среди i1,…,ik могут быть повторяющиеся)

43.

Пример
• Система Поста:
X=( 1=110, 2=01, 3=1)
Y=( 1=1, 2=10, 3=011)
• Решение
1 1 3 3 =11011011= 1 1 3 3

44.

Доказательство
• Граф
• Полурешётка
L={0 1} X* X*
• Частичный порядок
: 0 1 b
• Начальная разметка
0(ai) = ( i, i)
0(bi) = 1
0(c) = 1
1
a1
a1
…
an
с
b2 ...
b1

45.

Доказательство
• Функции пронесения
f(ai,bi)( ) = f(bj,bi)( ) = i i
f(ai,c)( ) = f(bj,c)( ) = 0
f(e1,e2)(x) = 1, иначе
a1
a1
…
an
с
b1
b2 ...
b1

46.

Доказательство
H (c )= 0
⇔∃ i 1 ,i 2 ,...,i k :f (bi ,c)f ( bi k− 1 ,bi k )... f ( ai 1 ,bi 2 )μ0 (ai 1 )= 0
k
⇔∃ i 1 ,i 2 ,...,i k :f (bi ,c)f ( bi k− 1 ,bi k )... f ( ai 1 ,bi 2 )(α i 1, βi 1)= 0
k
⇔∃ i 1 ,i 2 ,...,i k :f (bi ,c)(α i 1 α i 2... αi k , βi 1 βi 2 ... βi k )= 0
k
⇔∃ i 1 ,i 2 ,...,i k :α i α i 2 ...αi k = βi 1 βi 2 ... βi k
1
• То есть, если бы можно узнать точное
решение для дуги c, то можно было бы
решить проблему Поста
• Конец доказательства.