Введение в метрологию. Лекция №1

1. Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Башкирский

государственный университет»
Лекция №1
ВВЕДЕНИЕ В МЕТРОЛОГИЮ
Метрология

2.

4
•XVIII век — установление эталона метра (эталон хранится во Франции, в
Музее мер и весов; в настоящее время является в большей степени
историческим экспонатом, нежели научным инструментом);
•1832 год — создание Карлом Гауссом абсолютных систем единиц;
•1875 год — подписание международной Метрической конвенции;
•1960 год — разработка и установление Международной системы
единиц (СИ);
•XX век — метрологические исследования отдельных стран координируются
Международными метрологическими организациями.
Вехи отечественной истории метрологии:
•1893 год — создание Д. И. Менделеевым Главной палаты мер и весов
(современное название: «Научно-исследовательский институт метрологии им.
Менделеева»);
Всемирный день метрологии отмечается ежегодно 20 мая. Праздник учрежден
Международным Комитетом мер и весов (МКМВ) в октябре 1999 года, на 88
заседании МКМВ.
Метрология

3.

Предмет метрологии
2
«Метрология» происходит от двух греческих слов: metron, что переводится как «мера», и
logos – «учение». Наука об измерениях, методах и средствах обеспечения их единства
и способах достижения требуемой точности. Предметом метрологии является извлечение
количественной информации о свойствах объектов с заданной точностью и
достоверностью; нормативная база для этого — метрологические стандарты. Бурное
развитие метрологии пришлось на конец XX в. Оно неразрывно связано с развитием
новых технологий.
Метрология состоит из 3 разделов:
•Теоретическая
Рассматривает
общие
теоретические
проблемы
(разработка теории и проблем
измерений
физических
величин, их единиц, методов
измерений).
•Прикладная
Изучает вопросы практического
применения
разработок
теоретической метрологии. В её
ведении находятся все вопросы
метрологического обеспечения.
•Законодательная
Устанавливает обязательные
технические и юридические
требования по применению
единиц физической величины,
методов и средств измерений.
Метрология

4.

3
Цели и задачи метрологии:
•Создание общей теории измерений;
•образование единиц физических величин и систем единиц;
•разработка
и
стандартизация
методов
и
средств
измерений,
методов
определения точности измерений, основ обеспечения единства измерений и единообразия средств
измерений;
•создание эталонов и образцовых средств измерений, поверка мер и средств измерений.
Аксиомы метрологии:
•Любое измерение есть сравнение.
•Любое измерение без априорной информации (предварительных данных) невозможно.
•Результат любого измерения без округления значения является случайной величиной.
Объекты метрологии:
1) единицы измерения величин;
2) средства измерений;
3) методики, используемые для выполнения измерений и т.д.
Метрология

5.

Термины
5
•Единство измерений — состояние измерений, характеризующееся тем, что их результаты
выражаются в узаконенных единицах, размеры которых в установленных пределах равны
размерам единиц, воспроизводимым первичными эталонами, а погрешности результатов
измерений известны и с заданной вероятностью не выходят за установленные пределы.
•Физическая величина — одно из свойств физического объекта, общее в качественном
отношении для многих физических объектов, но в количественном отношении индивидуальное
для каждого из них.
•Средство измерений — техническое средство, предназначенное для измерений и имеющее
нормированные метрологические характеристики.
•Поверка - совокупность операций, выполняемых в целях подтверждения соответствия средств
измерения метрологическим требованиям.
•Погрешность измерения — отклонение результата измерения от истинного значения
измеряемой величины.
•Погрешность средства измерения — разность между показанием средства измерений и
действительным значением измеряемой физической величины.
•Точность средства измерений — характеристика качества средства измерений, отражающая
близость его погрешности к нулю.
•Лицензия — это разрешение, выдаваемое органам государственной метрологической службы
на закрепленной за ним территории физическому или юридическому лицу на осуществление
ему деятельности по производству и ремонту средств измерения.
•Эталон единицы величины - техническое средство предназначенное для передачи, хранения и
воспроизведения единицы величины.
Метрология

6.

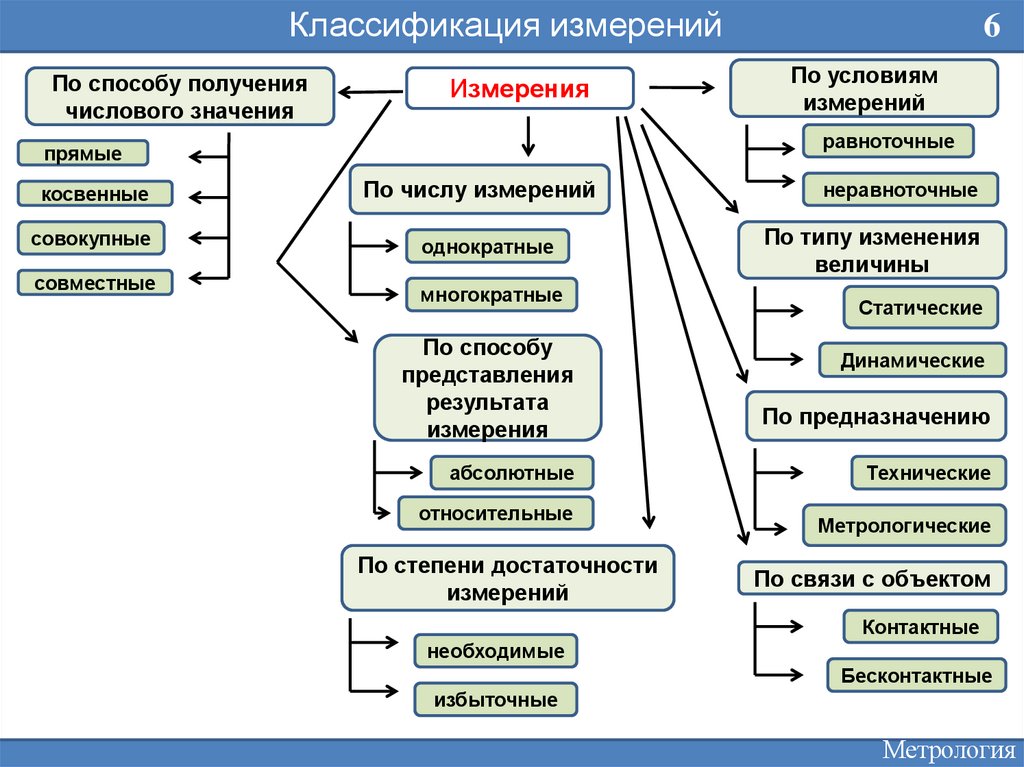
Классификация измерений
По способу получения
числового значения
Измерения
По условиям
измерений
равноточные
прямые
косвенные
По числу измерений
совокупные
однократные
совместные
6
многократные
По способу
представления
результата
измерения
абсолютные
относительные
По степени достаточности
измерений
неравноточные
По типу изменения
величины
Статические
Динамические
По предназначению
Технические
Метрологические
По связи с объектом
Контактные
необходимые
Бесконтактные
избыточные
Метрология

7.

7
Прямыми называются измерения, при которых значение величины
находят непосредственно из опытных данных.
Примеры прямых
измерений: измерение длины линейкой, температуры – термометром,
электрического напряжения – вольтметром. Уравнение
прямого
измерения: у = Сх, где С - цена деления СИ. Прямые измерения основа более сложных видов измерений.
Косвенными называют измерения, результат которых определяют на
основе прямых измерений величин, связанных с измеряемой величиной
известной зависимостью
у = f1(х1, х2, xn …..), где x1, х2, xn - результаты
прямых измерений, y - измеряемая величина.
Примеры: объем прямоугольного параллелепипеда определяется по
результатам прямых измерений длины в трех взаимно перпендикулярных
направлениях; электрическое сопротивление — по результатам измерений
падения напряжения и силы тока и т.д.
Абсолютное измерение - это косвенное измерение, для осуществления
которого используются прямое измерение массы, длины и времени.
Метрология

8.

8
Совокупные измерения значения измеряемых величин находят по
данным повторных измерений одной или нескольких одноименных величин
при различных сочетаниях мер или этих величин. Результаты совокупных
измерений находят путем решения системы уравнений, составляемых по
результатам нескольких прямых измерений.
При определении взаимоиндуктивности катушки М, например,
используют два метода: сложения и вычитания полей. Если индуктивность
одной из них L1, а другой – L2, то находят L01 = L1 + L2 + 2М и L02 =L1 +L2 - 2М,
отсюда
2M= L01 - L1 - L2
M = L01 - L1 - L2 / 2
2M= L02 - L1 - L2
M = L02 - L1 - L2 / 2
L01 - L1 - L2 / 2 = L02 - L1 - L2 / 2
М = (L01-L02)/4.
Метрология

9.

Совместные измерения
9
Совместными называют производимые одновременно (прямые или косвенные)
измерения двух или нескольких не одноименных величин. Целью совместных измерений
является нахождение функциональной зависимости одной величины от другой, например,
зависимости длины тела от температуры, зависимости электрического сопротивления
проводника от давления и т.п. Например, измерение сопротивления Rt, проводника при
фиксированной температуре t по формуле, Rt =R0 (1 + αt), где R0 - сопротивление при известной
температуре t0 (обычно 20°С) и α – температурный коэффициент – это величины постоянные,
измеренные косвенным методом: Δt = t - t0 — разность температур: t – заданное значение
температуры, измеренное прямым методом.
Пусть, например, известна функциональная связь вида Rt = R0 (1 + αt + βt2), т.е. связь
между сопротивлением Rt , при любой температуре t и сопротивлением R0 при t=0 и
постоянными коэффициентами α и β. Необходимо определить значения R0, α и β.
Для решения этой задачи используется совместный вид измерения. При трех известных
значениях температур t1, t2, t3 измеряются прямым способом Rt1, Rt2 и Rt3, затем составляется
система уравнений, решение которой позволяет определить искомые величины
R0 (1 + αt1 + βt12) = Rt1
R0 (1 + αt2 + βt22) = Rt2
R0 (1 + αt3 + βt32) = Rt3
Эти уравнения называются условными. Они представляют зависимость R от t при
фиксированных значениях t. Иначе говоря, совместные измерения позволяют получить систему
уравнений, связывающих зависимые величины между собой при различных их значениях.
Метрология

10.

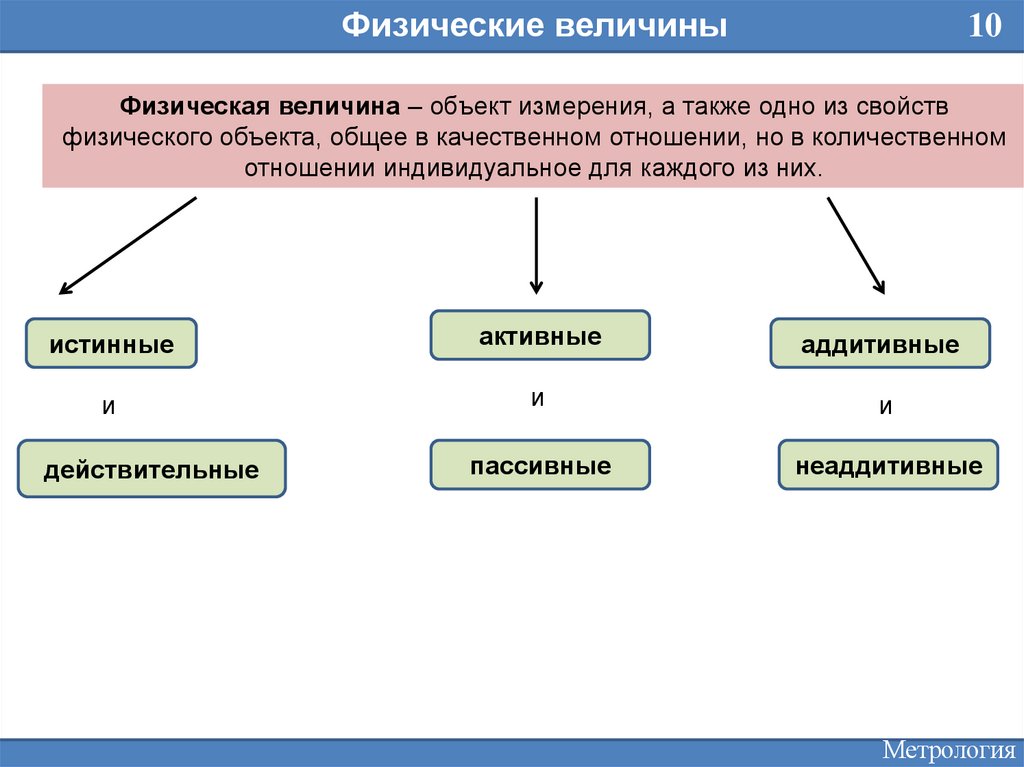
Физические величины
10
Физическая величина – объект измерения, а также одно из свойств
физического объекта, общее в качественном отношении, но в количественном
отношении индивидуальное для каждого из них.
истинные
активные
аддитивные
и
и
и
пассивные
неаддитивные
действительные
Метрология

11.

Размерность
11
Размерность - качественная характеристика измеряемых величин
Размерность обозначается символом dim, происходит от слова dimension.
Размерность физической величины dim Q - выражение в форме степенного многочлена,
составленного из произведений символов основных физических величин в различных
степенях
dim Q=LαMβTγIη,
Где L M T I - размерности физических величин,
α β γ η - показатели размерности.
Правила:
•Размерности левой и правой частей уравнения равны между собой.
•Алгебра
размерностей
мультипликативна,
т.е.
состоит
всего
лишь
из
двух действий - умножения и деления.
•Размерность произведения нескольких величин равна произведению их размерностей. Так,
если зависимость между величинами имеет вид Q=A·B·C, то dim Q = dimA · dimB · dimC.
• Размерность частного при делении одной величины на другую равна отношению их
размерностей, т.е. если Q = A/B, то dim Q = dimA / dimB.
• Размерность любой величины, возведенной в степень, равна её размерности в той же
степени. Так, если Q = Аn, то dim Q = dimАn
Метрология

12.

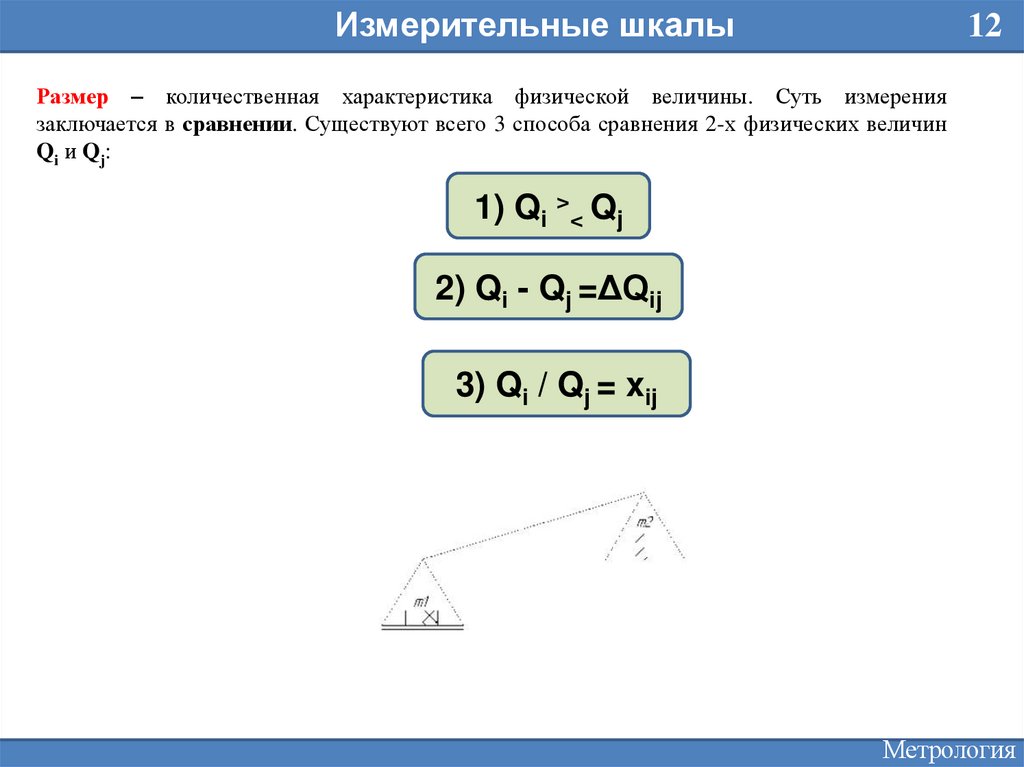
Измерительные шкалы
12
Размер – количественная характеристика физической величины. Суть измерения
заключается в сравнении. Существуют всего 3 способа сравнения 2-х физических величин
Qi и Qj:
1) Qi >< Qj
2) Qi - Qj =ΔQij
3) Qi / Qj = xij
Метрология

13.

Шкалы
13
ШКАЛЫ
Неметрические
Метрические
Шкала
наименований
Шкала интервалов
Шкала порядка
Шкала отношений
Абсолютные
шкалы
Метрология

14.

Шкала наименований (шкала классификаций)
14
- Классификация болезней с помощью диагностических средств
- Классификация цветов (по атласу)
- В системе пожаротушения сигнал «пожар» (если температура
превышает определённое значение) или «нет пожара» (ниже
значения)
- Классификация флоры и фауны
- Контроль изделий «годные» и «бракованные»
Метрология

15.

Шкала порядка (шкала рангов)
15
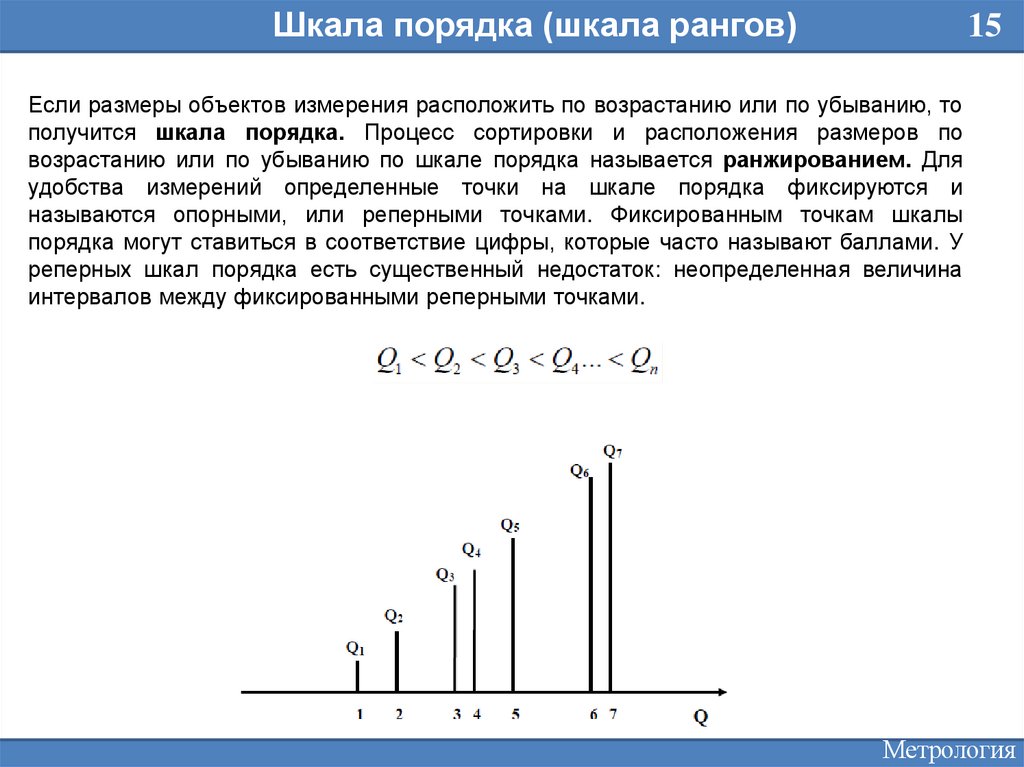
Если размеры объектов измерения расположить по возрастанию или по убыванию, то
получится шкала порядка. Процесс сортировки и расположения размеров по
возрастанию или по убыванию по шкале порядка называется ранжированием. Для
удобства измерений определенные точки на шкале порядка фиксируются и
называются опорными, или реперными точками. Фиксированным точкам шкалы
порядка могут ставиться в соответствие цифры, которые часто называют баллами. У
реперных шкал порядка есть существенный недостаток: неопределенная величина
интервалов между фиксированными реперными точками.
Метрология

16.

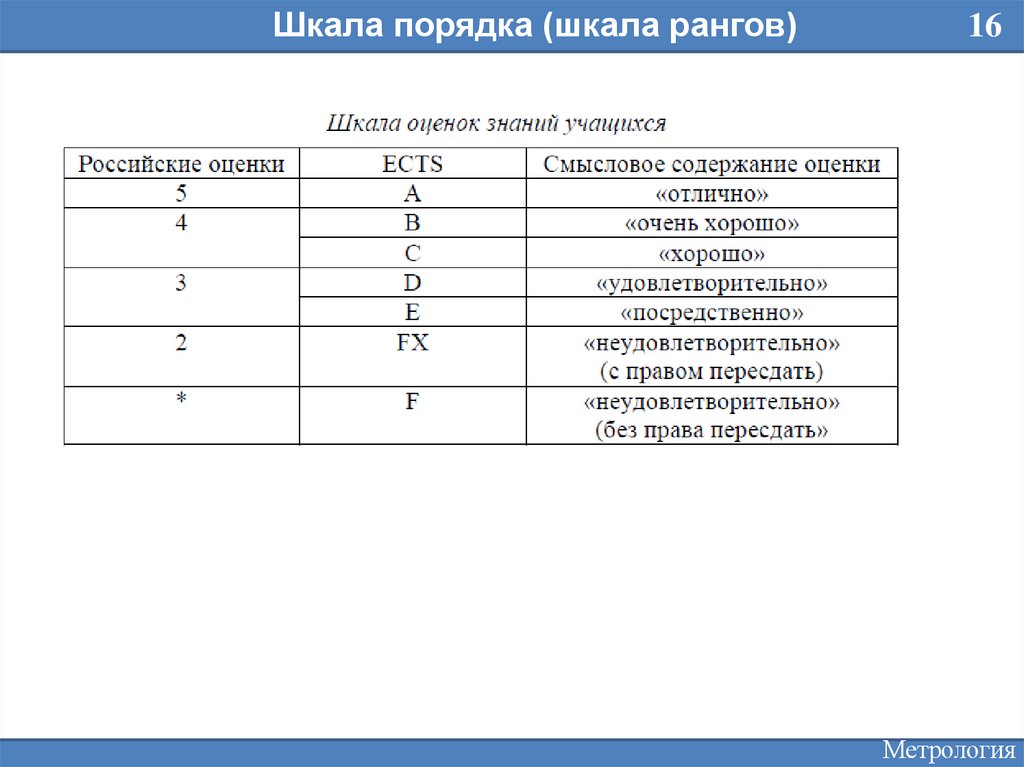
Шкала порядка (шкала рангов)
16
Метрология

17.

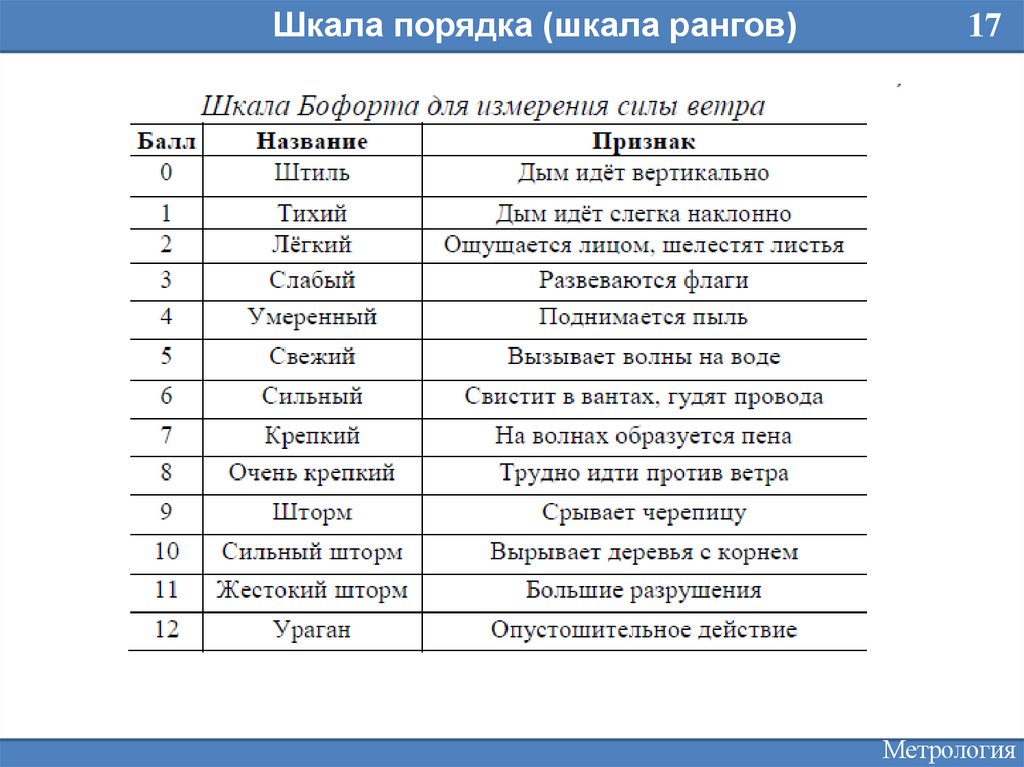
Шкала порядка (шкала рангов)
17
Метрология

18.

Шкала интервалов (шкала разностей)
18
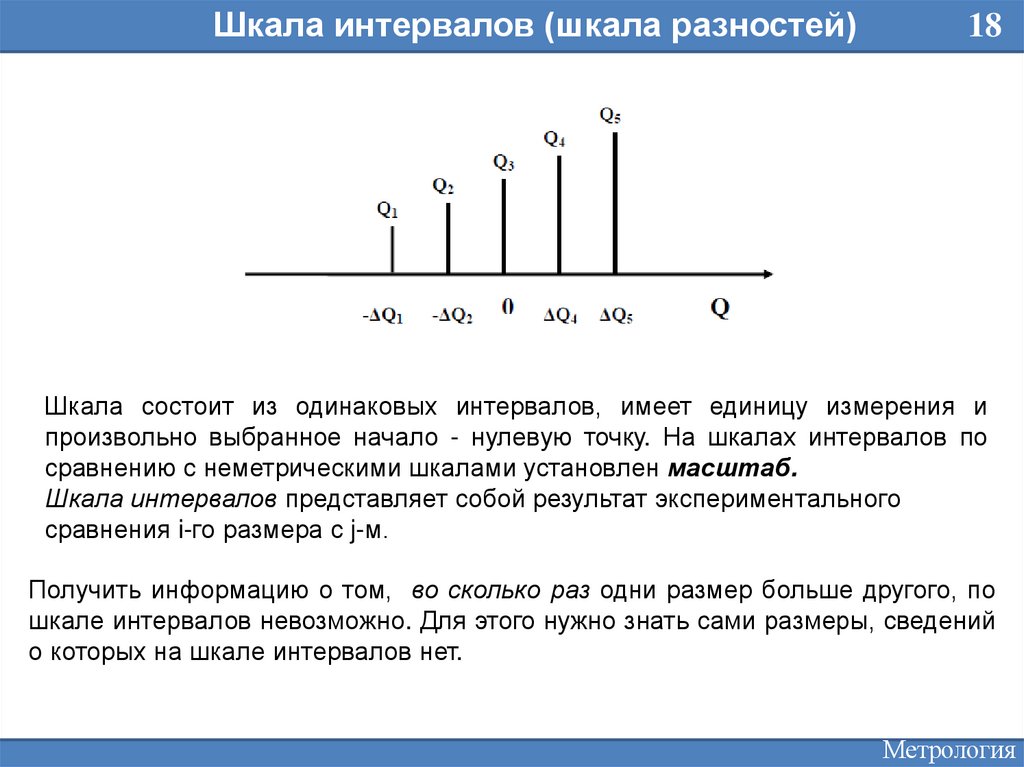
Шкала состоит из одинаковых интервалов, имеет единицу измерения и
произвольно выбранное начало - нулевую точку. На шкалах интервалов по
сравнению с неметрическими шкалами установлен масштаб.
Шкала интервалов представляет собой результат экспериментального
сравнения i-го размера с j-м.
Получить информацию о том, во сколько раз одни размер больше другого, по
шкале интервалов невозможно. Для этого нужно знать сами размеры, сведений
о которых на шкале интервалов нет.
Метрология

19.

Шкала отношений
19
Шкалы
отношений
являются
самыми
совершенными,
самыми
информативными и самыми распространёнными. На них представлена
информация о самих размерах физических величин, в частности - об их
значениях. Это позволяет решать и на сколько, и во сколько раз один размер
больше или меньше другого. На шкале отношений определены любые
математические операции.
Метрология

20.

Абсолютные шкалы
20
Примеры:
- Коэффициент трения
- Коэффициент затухания
- Коэффициент полезного действия (КПД)
- Вероятность
Относительные величины могут выражаться в
безразмерных единицах (когда отношение двух одноименных
величин равно 1), в процентах % (когда отношение равно 10-2),
промилле %0 (когда отношение равно 10-3), или
в миллионных долях ppm (когда отношение равно 10-6).
Метрология

21.

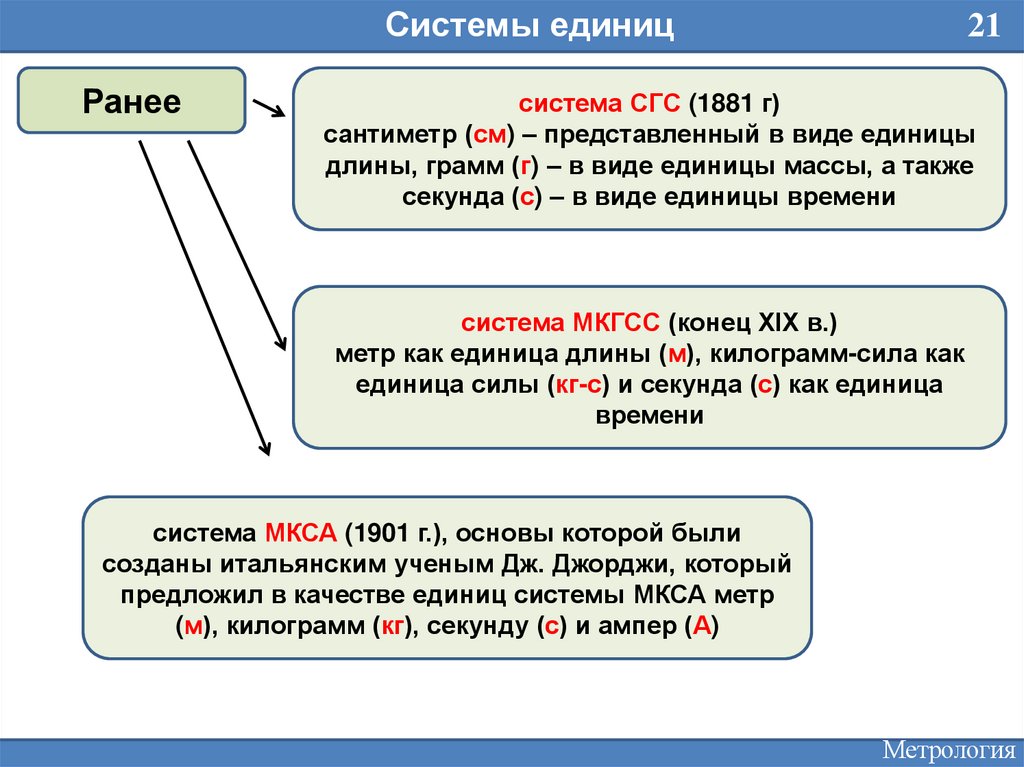
Системы единиц
Ранее
21
система СГС (1881 г)
сантиметр (см) – представленный в виде единицы
длины, грамм (г) – в виде единицы массы, а также
секунда (с) – в виде единицы времени
система МКГСС (конец XIX в.)
метр как единица длины (м), килограмм-сила как
единица силы (кг-с) и секунда (с) как единица
времени
система МКСА (1901 г.), основы которой были
созданы итальянским ученым Дж. Джорджи, который
предложил в качестве единиц системы МКСА метр
(м), килограмм (кг), секунду (с) и ампер (А)
Метрология

22.

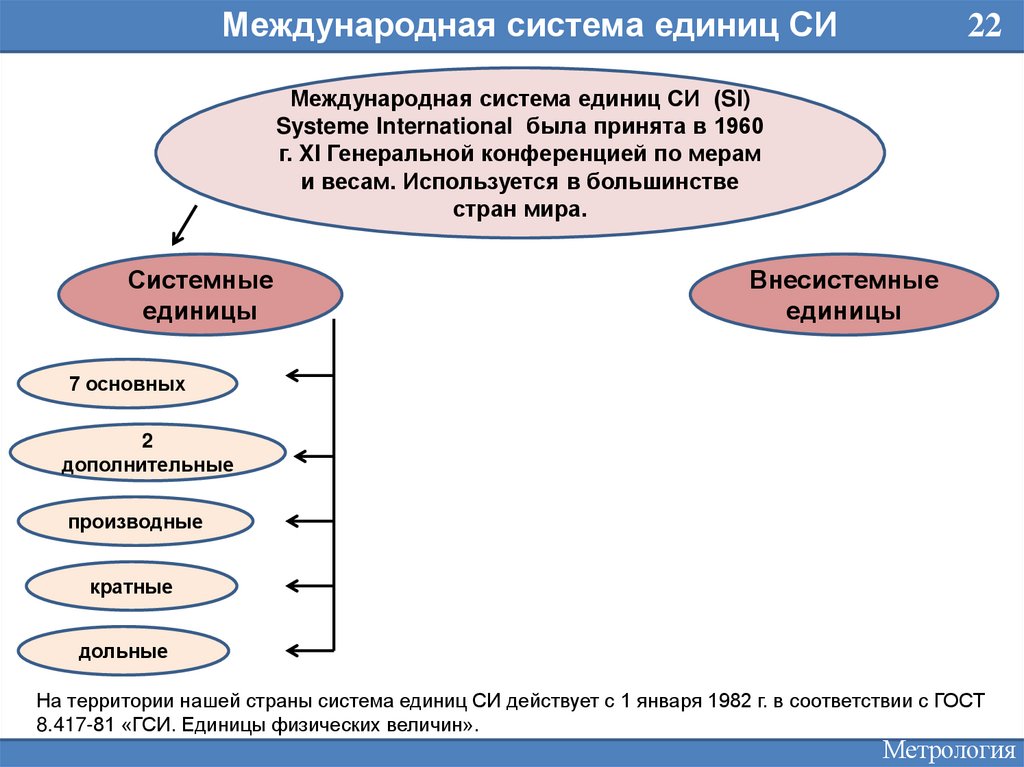
Международная система единиц СИ
22
Международная система единиц СИ (SI)
Systeme International была принята в 1960
г. XI Генеральной конференцией по мерам
и весам. Используется в большинстве
стран мира.
Системные
единицы
Внесистемные
единицы
7 основных
2
дополнительные
производные
кратные
дольные
На территории нашей страны система единиц СИ действует с 1 января 1982 г. в соответствии с ГОСТ
8.417-81 «ГСИ. Единицы физических величин».
Метрология

23.

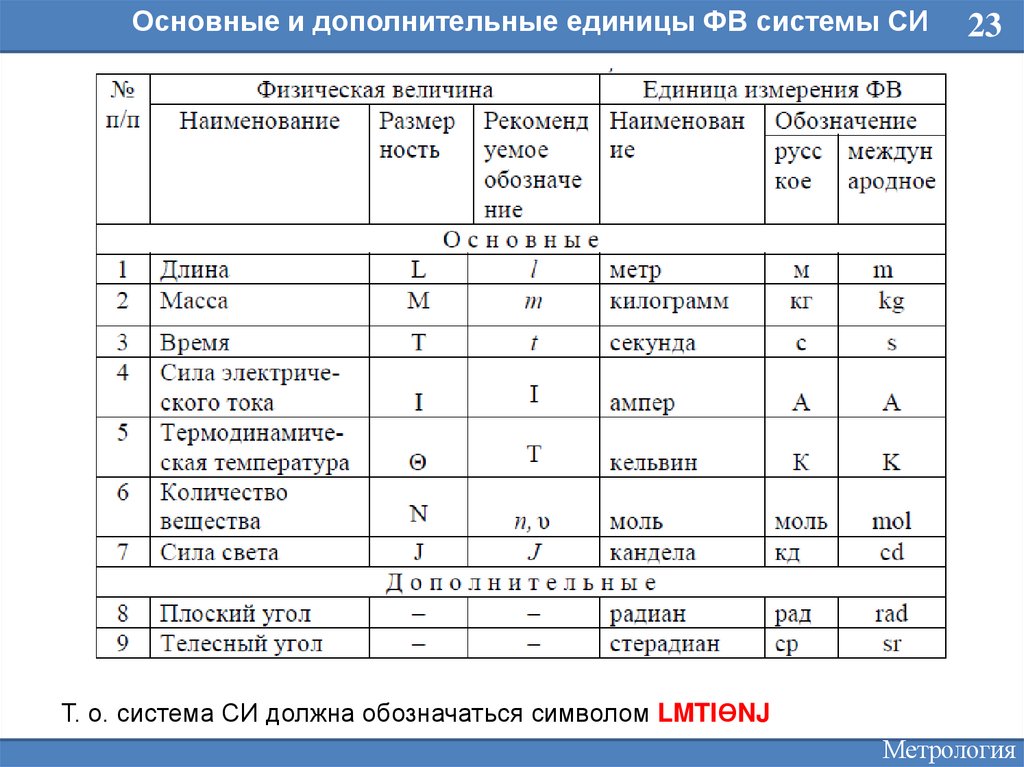
Основные и дополнительные единицы ФВ системы СИ
23
Т. о. система СИ должна обозначаться символом LMTIϴNJ
Метрология

24.

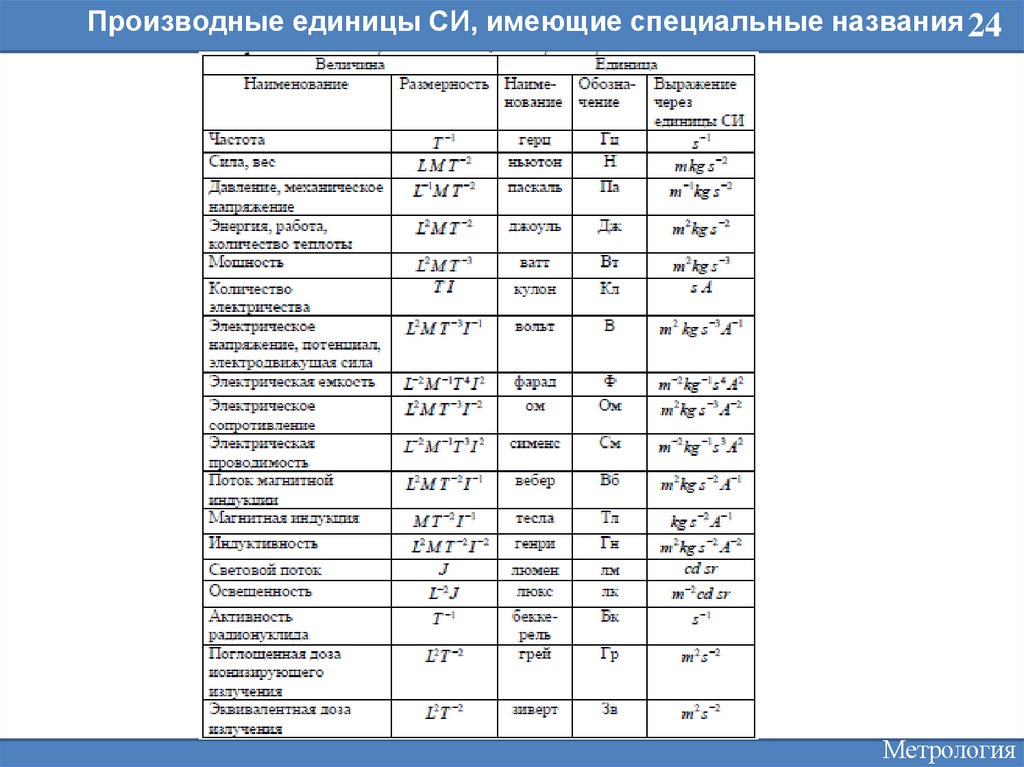
Производные единицы СИ, имеющие специальные названия 24
Метрология

25.

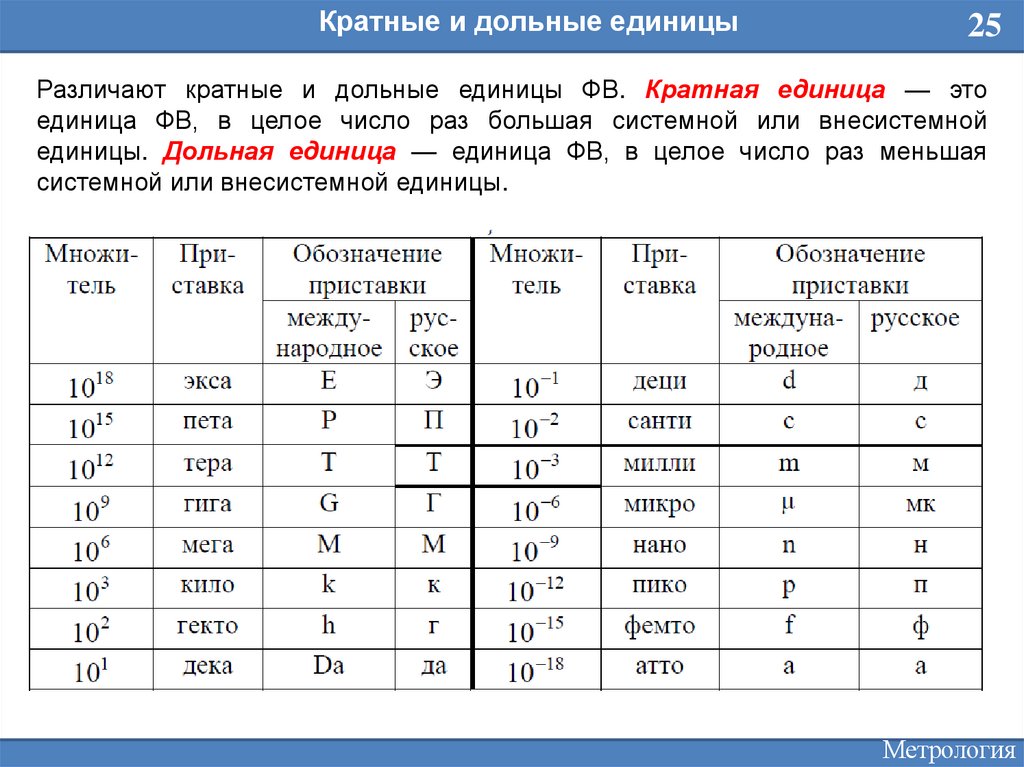
Кратные и дольные единицы
25
Различают кратные и дольные единицы ФВ. Кратная единица — это
единица ФВ, в целое число раз большая системной или внесистемной
единицы. Дольная единица — единица ФВ, в целое число раз меньшая
системной или внесистемной единицы.
Метрология

26.

Внесистемные единицы
26
1. Допускаемые наравне с единицами СИ, например: единица массы тонна; единицы плоского угла - градус, минута, секунда; единица объема
- литр и др.
2. Допускаемые к применению в специальных областях, к которым
относятся: единицы длины (в астрономии) - астрономическая единица,
парсек, световой год; единица оптической силы (в оптике) – диоптрия,
единица энергии (в физике) - электрон-вольт.
3. Временно допускаемые к применению наравне с единицами СИ,
например: в морской навигации — морская миля; в ювелирном деле
единица массы - карат и др. Эти единицы должны изыматься из
употребления в соответствии с международными соглашениями.
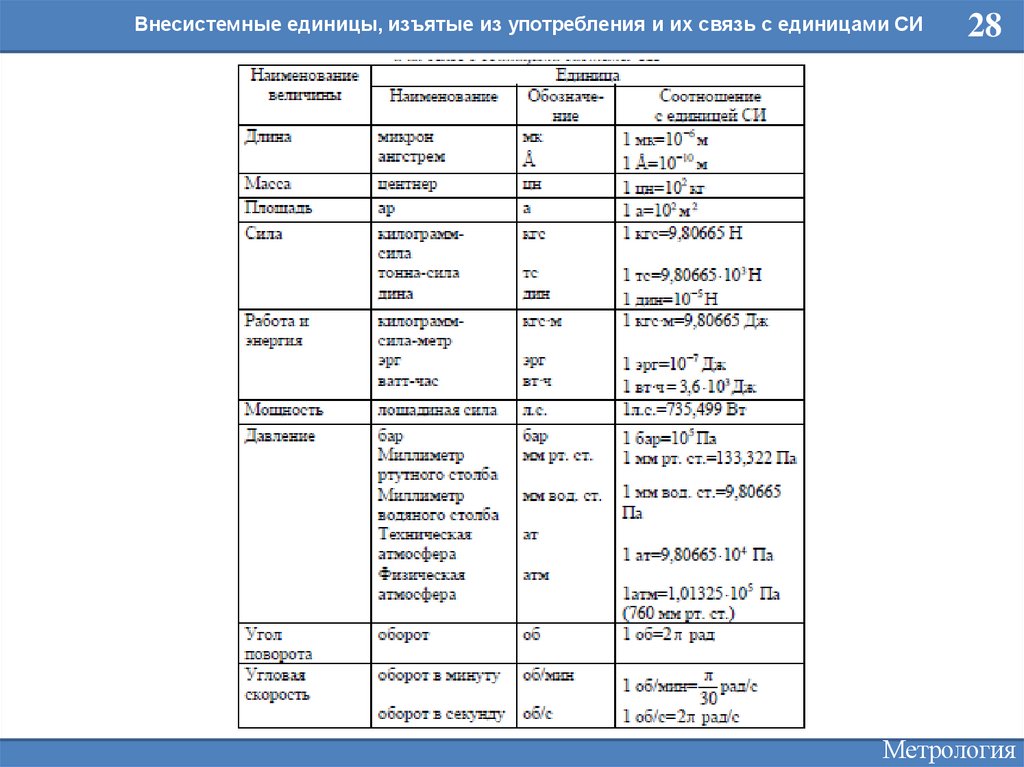
4. Изъятые из употребления, к ним относятся единицы давления миллиметр ртутного столба; единица мощности - лошадиная сила и др.
Метрология

27.

Внесистемные единицы, допускаемые к использованию наравне с единицами СИ
27
Метрология

28.

Внесистемные единицы, изъятые из употребления и их связь с единицами СИ
28
Метрология

29.

Основные единицы
29
Метр - длина пути, который проходит свет в вакууме за 1/299 792 458
долю секунды
Секунда равна 9 192 631 770 периодам излучения, соответствующего
переходу, который происходит между двумя сверхтонкими уровнями
основного состояния атома 133Cs
Килограмм представляет собой цилиндр диаметром и высотой
39,17 мм из платино-иридиевого сплава (90 % платины, 10 % иридия).
Ампер считается мерой той силы неизменяющегося тока,
вызывающего на каждом участке проводника длиной 1 м силу
взаимодействия при условии прохождения по двум прямолинейным
параллельным проводникам, обладающим такими показателями, как
ничтожно малая площадь кругового сечения и бесконечная длина, а
также расположение на расстоянии в 1 м друг от друга в условиях
вакуума
Метрология

30.

Основные единицы
30
Кельвин равен 1/273,16 части термодинамической температуры, так
называемой тройной точки воды
Моль – единица количества вещества, содержащая столько же
структурных единиц данного вещества , сколько атомов содержится
в 12 г углерода, состоящего из изотопа 12С
Кандела - сила света в заданном направлении источника,
испускающего монохроматическое излучение
частотой 540·1012 Гц, энергетическая сила света, которого в этом
направлении составляет 1/683 Вт/ср
Метрология

31.

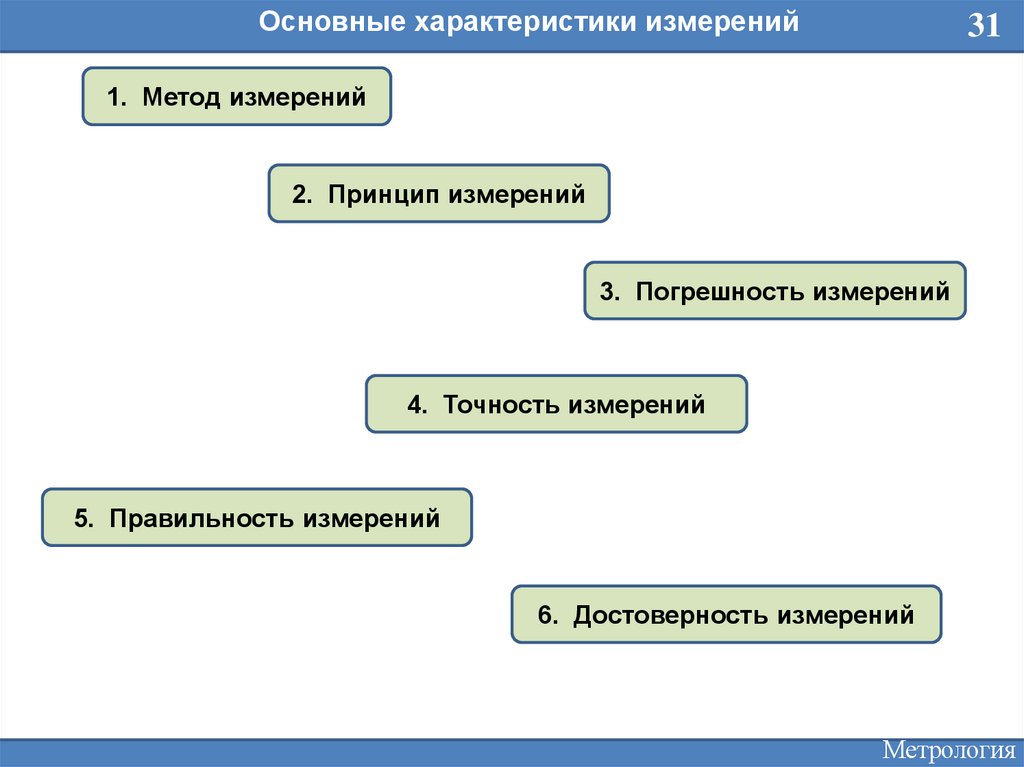
Основные характеристики измерений
31
1. Метод измерений
2. Принцип измерений
3. Погрешность измерений
4. Точность измерений
5. Правильность измерений
6. Достоверность измерений
Метрология

32.

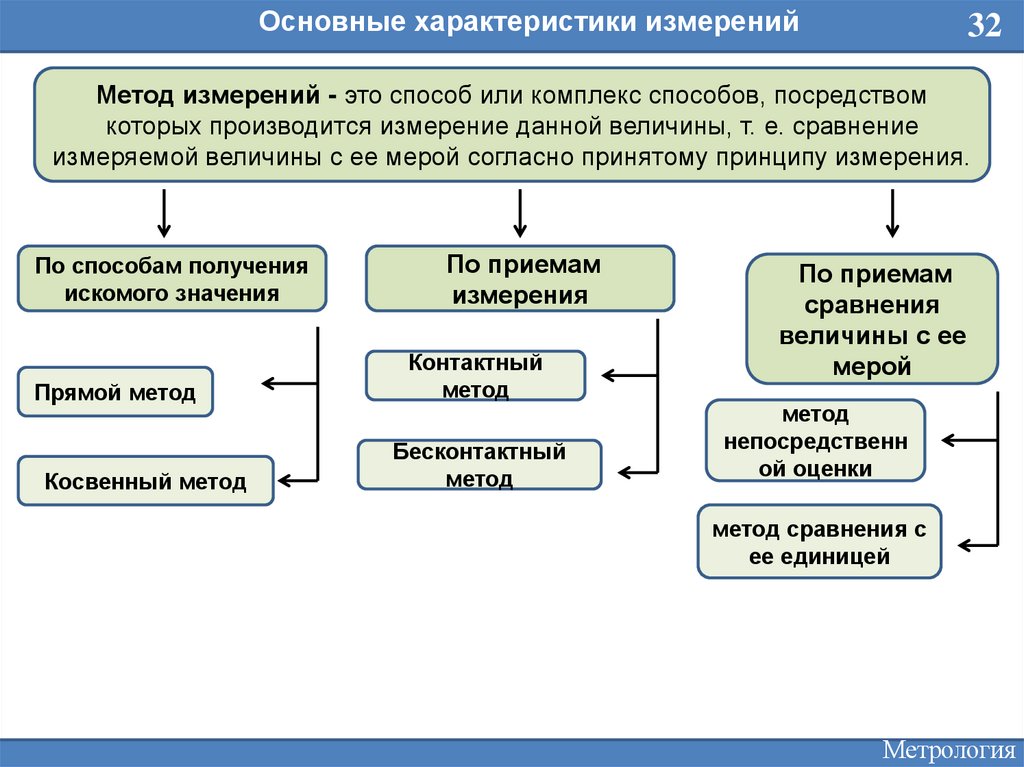
Основные характеристики измерений
32
Метод измерений - это способ или комплекс способов, посредством
которых производится измерение данной величины, т. е. сравнение
измеряемой величины с ее мерой согласно принятому принципу измерения.
По способам получения
искомого значения
По приемам
измерения
Прямой метод
Контактный
метод
Косвенный метод
Бесконтактный
метод
По приемам
сравнения
величины с ее
мерой
метод
непосредственн
ой оценки
метод сравнения с
ее единицей
Метрология

33.

Основные характеристики измерений
33
Принцип измерений – это некое физическое явление или их комплекс,
на которых базируется измерение. Например, измерение температуры
основано на явлении расширения жидкости при ее нагревании (ртуть
в термометре).
Погрешность измерения – это разность между результатом измерения
величины и настоящим (действительным) значением этой величины.
Погрешность, как правило, возникает из-за недостаточной точности
средств и методов измерения или из-за невозможности обеспечить
идентичные условия при многократных наблюдениях.
Точность измерений – это характеристика, выражающая степень
соответствия
результатов
измерения
настоящему
значению
измеряемой величины. Количественно точность измерений равна
величине относительной погрешности в минус первой степени,
взятой по модулю.
Метрология

34.

Основные характеристики измерений
34
Правильность измерения – это качественная характеристика
измерения, которая определяется тем, насколько близка к нулю
величина постоянной или фиксировано изменяющейся при
многократных
измерениях
погрешности
(систематическая
погрешность). Данная характеристика зависит, как правило, от
точности средств измерений.
Основная характеристика измерений – это достоверность
измерений.
Достоверность
измерений
–
это
характеристика,
определяющая степень доверия к полученным результатам
измерений. По данной характеристике измерения делятся на
достоверные и недостоверные. Достоверность измерений зависит
того, известна ли вероятность отклонения результатов измерения от
настоящего значения измеряемой величины. Если же достоверность
измерений не определена, то результаты таких измерений, как
правило, не используются. Достоверность измерений ограничена
сверху погрешностью измерений.
Метрология