Similar presentations:
Метрология, стандартизация и сертификация
1.
МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯИ СЕРТИФИКАЦИЯ
2.
Раздел 1МЕТРОЛОГИЯ
3.
Тема 1.1ОСНОВНЫЕ ПОНЯТИЯ
4.
Триада методов и видов деятельности пообеспечению качества
5.
МЕТРОЛОГИЯРекомендации по межгосударственной
стандартизации
РМГ 29–99 «ГСИ. Метрология.
Основные термины и определения»
Метрология – это наука об измерениях, методах и
средствах обеспечения их единства и способах
достижения требуемой точности.
др. греч. μετρον – мера,
λογοζ – наука, учение
6.
7.
МЕТРОЛОГИЯТеоретическая
(фундаментальная)
Метрология
Законодательная
Практическая
(прикладная)
8.
МЕТРОЛОГИЯТеоретическая (фундаментальная) метрология
Раздел метрологии, предметом которого
является разработка фундаментальных основ
метрологии.
9.
МЕТРОЛОГИЯЗаконодательная метрология
Раздел метрологии, предметом которого
является установление обязательных
технических и юридических требований по
применению единиц физических величин,
эталонов, методов и средств измерений,
направленных на обеспечение единства и
необходимости точности измерений в интересах
общества.
10.
МЕТРОЛОГИЯПрактическая (прикладная) метрология
Раздел метрологии, предметом которого
являются вопросы практического применения
разработок теоретической метрологии и
положений законодательной метрологии.
11.
СВОЙСТВОВсе объекты окружающего мира
характеризуются своими свойствами.
Свойство
Философская категория, выражающая такую
сторону объекта (явления процесса), которая
обусловливает его различие или общность с
другими объектами (явлениями, процессами) и
обнаруживается в его отношениях к ним.
Свойство – категория качественная.
12.
ВЕЛИЧИНАДля количественного описания различных
свойств процессов и физических тел вводится
понятие величины.
Величина
Свойство чего-либо, что может быть выделено
среди других свойств и оценено тем или иным
способом, в том числе и количественно.
Величина не существует сама по себе, она имеет
место лишь постольку, поскольку существует
объект со свойствами, выраженными данной
величиной.
13.
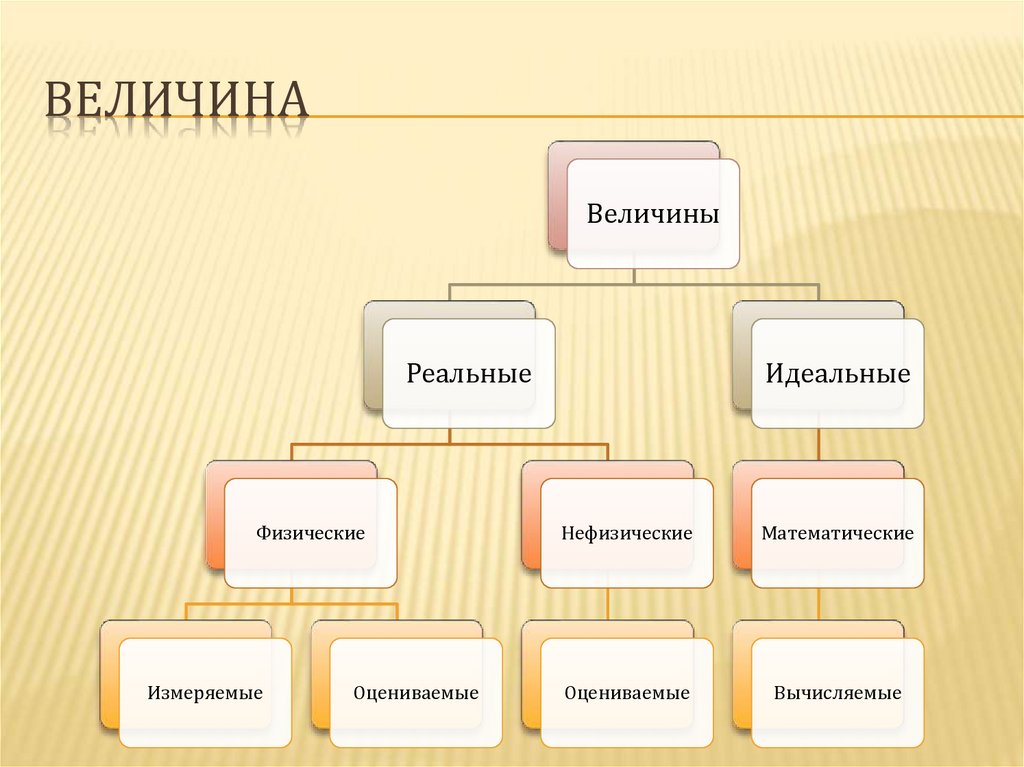
ВЕЛИЧИНАВеличины
Реальные
Физические
Измеряемые
Оцениваемые
Идеальные
Нефизические
Математические
Оцениваемые
Вычисляемые
14.
ВЕЛИЧИНАФизическая величина (ФВ)
Одно из свойств физического объекта
(физической системы, явления или процесса),
общее в качественном отношении для многих
физических объектов, но в количественном
отношении индивидуальное для каждого из них.
Физические величины – это измеренные
свойства физических объектов и процессов, с
помощью которых они могут быть изучены.
15.
ВЕЛИЧИНАНефизические величины, для которых единица
измерения в принципе не может быть введена,
могут быть только оценены.
Оценивание нефизических величин не входит в
задачи теоретической метрологии.
16.
ВЕЛИЧИНАВеличины
Реальные
Физические
Измеряемые
Оцениваемые
Идеальные
Нефизические
Математические
Оцениваемые
Вычисляемые
17.
ФИЗИЧЕСКАЯ ВЕЛИЧИНАРазмер ФВ
Количественная определенность физической
величины, присущая конкретному
материальному объекту, системе, явлению или
процессу
Значение ФВ
Q
Выражение размера физической величины в
виде некоторого числа принятых для нее единиц
18.
ФИЗИЧЕСКАЯ ВЕЛИЧИНАЧисловое значение ФВ
q
Отвлеченное число, входящее в значение
величины
Единица измерения ФВ
[Q]
ФВ фиксированного размера, которой условно
присвоено числовое значение, равное 1, и
применяемая для количественного выражения
однородных с ней ФВ
19.
ФИЗИЧЕСКАЯ ВЕЛИЧИНАОсновное уравнение измерения
Q = q[Q]
Суть простейшего измерения состоит в
сравнении ФВ Q с размерами выходной величины
регулируемой многозначной меры q[Q].
В результате сравнения устанавливают, что
q[Q] < Q < (q + 1)[Q]
Измерение – познавательный процесс,
заключающийся в сравнении путем физического
эксперимента данной ФВ с известной ФВ,
принятой за единицу измерения.
20.
ФИЗИЧЕСКАЯ ВЕЛИЧИНАРазмер ФВ оценивают и измеряют при помощи
шкал.
Шкала ФВ
Упорядоченная совокупность значений
физической величины, служащая исходной
основой для измерений данной величины.
21.
ВИДЫ ШКАЛ22.
Тема 1.2СИСТЕМЫ ФИЗИЧЕСКИХ ВЕЛИЧИН
И ИХ ЕДИНИЦ
23.
РАЗМЕРНОСТЬ ФВРазмерность ФВ
dim Q
Выражение в форме степенного многочлена, отражающее
связь данной величины с основными ФВ. Коэффициент
пропорциональности принят равным единице:
dim Q = LαMβTγIη…,
где L, М, Т, I – условные обозначения основных величин
данной системы;
α, β, γ, η – целые или дробные, положительные или
отрицательные вещественные числа (показатели
размерности).
Если все показатели размерности равны нулю, то такую
величину называют безразмерной.
24.
РАЗМЕРНОСТЬ ФВФВ
Размерные
Безразмерные
25.
СИСТЕМА ФИЗИЧЕСКИХ ВЕЛИЧИНСистема ФВ
Совокупность физических величин,
образованная в соответствии с принятыми
принципами, когда одни величины принимают за
независимые, а другие определяют как функции
независимых величин.
26.
СИСТЕМА ФИЗИЧЕСКИХ ВЕЛИЧИНОсновная и производная ФВ
Основная ФВ
ФВ, входящая в систему величин и условно
принятая в качестве независимой от других
величин этой системы.
Производная ФВ
ФВ, входящая в систему величин и определяемая
через основные величины этой системы.
27.
СИСТЕМА ФИЗИЧЕСКИХ ВЕЛИЧИНОсновные и производные единицы ФВ
Единицы основных или производных ФВ также
называют, соответственно, основными или
производными единицами ФВ.
28.
СИСТЕМА ФИЗИЧЕСКИХ ВЕЛИЧИНВ Российской Федерации используется система единиц СИ в соответствии с ГОСТ
8.417–2002 «ГСИ. Единицы величин».
29.
СИСТЕМА ФИЗИЧЕСКИХ ВЕЛИЧИН30.
Тема 1.3ВИДЫ И МЕТОДЫ ИЗМЕРЕНИЙ
31.
32.
ВИДЫ ИЗМЕРЕНИЙ1) По особенностям обработки результатов измерения:
Равноточные измерения
Ряд измерений какой-либо величины, выполненных
одинаковыми по точности средствами измерений в одних
и тех же условиях с одинаковой тщательностью.
Примечание. Прежде чем обрабатывать ряд измерений,
необходимо убедиться в том, что все измерения этого
ряда являются равноточными.
Неравноточные измерения
Ряд измерений какой-либо величины, выполненных
различающимися по точности средствами измерений и
(или) в разных условиях.
33.
ВИДЫ ИЗМЕРЕНИЙ2) По количеству выполненных наблюдений или снятых
показаний средств измерения:
Однократное измерение
Измерение, выполненное один раз.
Многократное измерение
Измерение физической величины одного и того же
размера, результат которого получен из нескольких
следующих друг за другом измерений, т.е. состоящее из
ряда однократных измерений.
34.
ВИДЫ ИЗМЕРЕНИЙ3) По характеру зависимости измеряемой величины от
времени:
Статические измерения
Измерения, при которых измеряемая ФВ принимается за
неизменную, по крайней мере на время, необходимое для
проведения измерений.
Динамические измерения
Измерения, при которых измеряемая ФВ изменяется со
скоростью, превышающей возможности средства
измерений отслеживать изменение входной измеряемой
величины.
35.
ВИДЫ ИЗМЕРЕНИЙ2) В зависимости от способа получения результата
измерений или числового значения измеряемой ФВ:
Прямое измерение
Измерение, при котором искомое значение физической
величины получают непосредственно.
Пример:
измерение длины линейкой,
массы на весах,
силы тока амперметром и т.д.
36.
ВИДЫ ИЗМЕРЕНИЙ2) В зависимости от способа получения результата
измерений или числового значения измеряемой ФВ:
Косвенное измерение
Определение искомого значения физической величины
на основании результатов прямых измерений других
физических величин, функционально связанных с
искомой величиной.
Пример:
Определение плотности D тела цилиндрической формы
по результатам прямых измерений массы m, высоты h и
диаметра цилиндра d, связанных с плотностью
уравнением
m
D=
0,25πd2 h
37.
ВИДЫ ИЗМЕРЕНИЙ2) В зависимости от способа получения результата
измерений или числового значения измеряемой ФВ:
Совокупные измерения
Проводимые одновременно измерения нескольких
одноименных величин, при которых искомые значения
величин определяют путем решения системы уравнений,
получаемых при измерениях этих величин в различных
сочетаниях.
Пример:
Значение массы отдельных гирь набора определяют по
известному значению массы одной из гирь и по
результатам измерений (сравнений) масс различных
сочетаний гирь.
38.
ВИДЫ ИЗМЕРЕНИЙ2) В зависимости от способа получения результата
измерений или числового значения измеряемой ФВ:
Совместные измерения
Проводимые одновременно измерения двух или
нескольких неодноименных величин для определения
зависимости между ними.
Пример:
Измерение сопротивления Rt проводника при
фиксированной температуре t по формуле Rt = R0(1+ t),
где R0 и – сопротивление при известной температуре t0
(обычно 0 °С) и температурный коэффициент – величины
постоянные, измеренные косвенным методом; t = t – t0 –
разность температур; t – заданное значение температуры,
измеряемое прямым методом.
39.
МЕТОДЫ ИЗМЕРЕНИЙПринцип измерений
Физическое явление или эффект, положенное в основу
измерений.
Примеры:
Применение эффекта Зеебека для измерения
температуры
Применение эффекта Доплера для измерения скорости
Использование силы тяжести при измерении массы
взвешиванием
Метод измерений
Прием или совокупность приемов сравнения измеряемой
физической величины с ее единицей в соответствии с
реализованным принципом измерений.
40.
МЕТОДЫ ИЗМЕРЕНИЙМетод непосредственной оценки
Метод измерений, при котором значение
величины определяют непосредственно по
показывающему средству измерений.
41.
МЕТОДЫ ИЗМЕРЕНИЙМетод сравнения с мерой
Метод измерений, в котором измеряемую
величину сравнивают с величиной,
воспроизводимой мерой.
Примеры:
Измерение массы на рычажных весах с
уравновешиванием гирями (мерами массы с
известным значением).
Измерение напряжения постоянного тока на
компенсаторе сравнением с известной ЭДС
нормального элемента.
42.
МЕТОДЫ ИЗМЕРЕНИЙДифференциальный метод измерений
Метод измерений, при котором измеряемая
величина сравнивается с однородной величиной,
имеющей известное значение, незначительно
отличающееся от значения измеряемой
величины, и при котором измеряется разность
между этими двумя величинами.
Пример:
Измерения, выполняемые при поверке мер
длины сравнением с эталонной мерой на
компараторе.
43.
МЕТОДЫ ИЗМЕРЕНИЙНулевой метод измерений
Метод сравнения с мерой, в котором
результирующий эффект воздействия
измеряемой величины и меры на прибор
сравнения доводят до нуля.
Пример:
Измерения электрического сопротивления
мостом с полным его уравновешиванием.
44.
МЕТОДЫ ИЗМЕРЕНИЙМетод измерений дополнением
Метод сравнения с мерой, в котором значение
измеряемой величины дополняется мерой этой
же величины с таким расчетом, чтобы на прибор
сравнения воздействовала их сумма, равная
заранее заданному значению.
45.
МЕТОДЫ ИЗМЕРЕНИЙМетод измерений замещением
Метод сравнения с мерой, в котором измеряемую
величину замещают мерой с известным
значением величины.
Пример:
Взвешивание с поочередным помещением
измеряемой массы и гирь на одну и ту же
чашку весов (метод Борда).
46.
МЕТОДЫ ИЗМЕРЕНИЙМетодика выполнения измерений (МВИ)
Установленная совокупность операций и правил
при измерении, выполнение которых
обеспечивает получение результатов измерений
с гарантированной точностью в соответствии с
принятым методом.
Примечание:
Обычно методика измерений
регламентируется каким-либо нормативнотехническим документом.
47.
Тема 1.4РЕЗУЛЬТАТ ИЗМЕРЕНИЯ
48.
РЕЗУЛЬТАТ ИЗМЕРЕНИЯ49.
Тема 1.5УСЛОВИЯ ИЗМЕРЕНИЙ
50.
УСЛОВИЯ ИЗМЕРЕНИЙ51.
Тема 1.6ОБЕСПЕЧЕНИЕ ЕДИНСТВА ИЗМЕРЕНИЙ
52.
ОБЕСПЕЧЕНИЕ ЕДИНСТВА ИЗМЕРЕНИЙ53.
Тема 1.7ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
54.
ПОГРЕШНОСТИ ИЗМЕРЕНИЙИстинное значение ФВ
Значение ФВ, которое идеальным образом
характеризует в качественном и количественном
отношении соответствующую ФВ.
Примечание:
Истинное значение ФВ может быть соотнесено
с понятием абсолютной истины. Оно может
быть получено только в результате
бесконечного процесса измерений с
бесконечным совершенствованием методов и
средств измерений.
55.
ПОГРЕШНОСТИ ИЗМЕРЕНИЙДействительное значение ФВ
Значение ФВ, полученное экспериментальным
путем и настолько близкое к истинному
значению, что в поставленной измерительной
задаче может быть использовано вместо него.
56.
ПОГРЕШНОСТИ ИЗМЕРЕНИЙПогрешность результата измерения
xизм
Отклонение результата измерения от истинного
xи (действительного xд) значения измеряемой
величины:
xизм = xизм – xи
xизм = xизм – xд
Примечания:
Истинное значение величины неизвестно, его
применяют только в теоретических исследованиях.
На практике используют действительное значение
величины.
57.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ1) По форме выражения:
Абсолютная погрешность
Погрешность измерения, выраженная в единицах
измеряемой величины:
xизм = xизм – xд
Примечание :
Необходимо различать термины абсолютная
погрешность и абсолютное значение
погрешности – значение погрешности без
учета ее знака (модуль погрешности).
58.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ1) По форме выражения:
Относительная погрешность
Погрешность измерения, выраженная
отношением абсолютной погрешности
измерения к действительному или измеренному
значению измеряемой величины:
∆xизм
δ= ±
∙ 100%
xд
∆xизм
δ= ±
∙ 100%
xизм
59.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ1) По форме выражения:
Приведенная погрешность
Погрешность измерения, выраженная
отношением абсолютной погрешности
измерения к нормирующему значению
(некоторому условно принятому постоянному
значению величины)
∆xизм
γ= ±
∙ 100%,
xн
где xн – нормирующее значение ФВ (например,
максимальное значение измеряемой ФВ).
60.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ2) В зависимости от характера проявления:
Систематическая погрешность
Δс
Составляющая погрешности результата измерения,
остающаяся постоянной или закономерно изменяющаяся
при повторных измерениях одной и той же ФВ.
Примечание:
В зависимости от характера измерения
систематические погрешности подразделяют на:
постоянные,
прогрессивные,
периодические,
изменяющиеся по сложному закону.
61.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ2) В зависимости от характера проявления:
Систематическая погрешность
Постоянные погрешности
Погрешности, которые длительное время сохраняют
свое значение, например, в течение времени
выполнения всего ряда измерений. Они встречаются
наиболее часто.
Прогрессивные погрешности
Непрерывно возрастающие или убывающие
погрешности.
62.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ2) В зависимости от характера проявления:
Систематическая погрешность
Периодические погрешности
Погрешности, значение которых является
периодической функцией времени или перемещения
указателя измерительного прибора.
Погрешности, изменяющиеся по сложному закону
Происходят вследствие совместного действия
нескольких систематических погрешностей.
63.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ2) В зависимости от характера проявления:
Систематическая погрешность
Систематическая погрешность исключается из
результата измерения путем введения в него
поправки.
Поправка
Значение величины, вводимое в неисправленный
результат измерения с целью исключения составляющих
систематической погрешности.
Примечание:
Знак поправки противоположен:
xизм испр = xизм + c = xизм − Δc ,
где c = −Δc – поправка.
64.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ2) В зависимости от характера проявления:
Систематическая погрешность
Как правило, считают, что систематические
погрешности могут быть обнаружены и исключены.
Однако в реальных условиях полностью исключить
систематическую составляющую погрешности
невозможно. Всегда остаются какие-то неисключенные
остатки, которые и нужно учитывать, чтобы оценить
их границы. Это и будет систематическая погрешность
измерения. То есть, в принципе, систематическая
погрешность тоже случайна, и указанное деление
обусловлено лишь установившимися традициями
обработки и представления результатов измерения.
65.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ2) В зависимости от характера проявления:
Систематическая погрешность
Неисключенная систематическая погрешность
НСП
Составляющая погрешности результата измерений,
обусловленная погрешностями вычисления и введения
поправок на влияние систематических погрешностей или
систематической погрешностью, поправка на действие
которой не введена вследствие ее малости.
Примечание:
Иногда этот вид погрешности называют
неисключенный (-ные) остаток (остатки)
систематической погрешности.
66.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ2) В зависимости от характера проявления:
Случайная погрешность
Δሞ
Составляющая погрешности результата измерения,
изменяющаяся случайным образом (по знаку и
значению) при повторных измерениях, проведенных с
одинаковой тщательностью, одной и той же физической
величины.
Примечания:
В появлении таких погрешностей не наблюдается
какой-либо закономерности, они проявляются при
повторных наблюдениях в виде некоторого разброса
полученных результатов.
67.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ2) В зависимости от характера проявления:
Случайная погрешность
Примечания:
Случайные погрешности неустранимы и всегда
присутствуют в результате измерения.
Описание случайных погрешностей возможно на
основе теории случайных процессов и математической
статистики.
Уменьшение случайных погрешностей возможно путем
увеличения числа наблюдений. В основе теории
погрешностей лежат 2 положения, подтверждающиеся
практикой:
68.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ2) В зависимости от характера проявления:
Случайная погрешность
Примечания:
При большом числе измерений случайные
погрешности одинакового числового значения и
разного знака встречаются одинаково часто.
Большие по абсолютной величине погрешности
встречаются реже, чем малые.
Из первого положения следует важный вывод: при
увеличении числа измерений случайная погрешность
результата, полученного из серии измерений,
уменьшается, так как сумма погрешностей отдельных
измерений данной серии стремится к нулю.
69.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ2) В зависимости от характера проявления:
Грубые погрешности (промахи)
Погрешность результата отдельного измерения,
входящего в ряд измерений, которая для данных условий
резко отличается от остальных результатов этого ряда.
Примечания:
Грубые погрешности возникают из-за ошибочных
действий оператора, неисправности средства
измерений или резких изменений условий измерений.
Как правило, грубые погрешности выявляются в
результате обработки результатов измерений с
помощью специальных критериев.
70.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ3) В зависимости от источников возникновения:
Субъективная погрешность
Составляющая систематической погрешности измерений,
обусловленная индивидуальными особенностями
оператора.
Примечания:
Встречаются операторы, которые систематически
опаздывают (или опережают) снимать отсчеты
показаний средств измерений.
Иногда субъективную погрешность называют личной
погрешностью или личной разностью.
71.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ3) В зависимости от источников возникновения:
Инструментальная погрешность
Составляющая погрешности измерения, обусловленная
погрешностью применяемого средства измерений.
Погрешность метода
Составляющая систематической погрешности измерений,
обусловленная несовершенством принятого метода
измерений.
72.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ3) В зависимости от источников возникновения:
В ряде случаев систематическая погрешность может
быть исключена за счет устранения источников
погрешности до начала измерений (профилактика
погрешности), а в процессе измерений – путем
внесения известных поправок в результаты
измерений.
Профилактика погрешности – наиболее рациональный
способ ее снижения и заключается в устранении
влияния, например, температуры
(термостатированием и термоизоляцией), магнитных
полей (магнитными экранами), вибраций и т. п. Сюда
же относятся регулировка, ремонт и поверка СИ.
73.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ4) По зависимости погрешности измерения от времени:
Статическая погрешность
Погрешность результата измерений, свойственная
условиям статического измерения.
Динамическая погрешность
Погрешность результата измерений, свойственная
условиям динамического измерения.
74.
Тема 1.8НОРМИРОВАНИЕ МЕТРОЛОГИЧЕСКИХ
ХАРАКТЕРИСТИК СРЕДСТВ ИЗМЕРЕНИЙ
75.
СРЕДСТВА ИЗМЕРЕНИЙСредство измерений
СИ
Техническое средство, предназначенное для
измерений, имеющее нормированные
метрологические характеристики,
воспроизводящее и (или) хранящее единицу
физической величины, размер которой
принимают неизменным (в пределах
установленной погрешности) в течение
известного интервала времени.
76.
КЛАССИФИКАЦИЯ СИ77.
МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИГОСТ 8.009–84 «ГСИ. Нормируемые метрологические
характеристики средств измерений» устанавливает
перечень MX СИ, способы их нормирования и формы
представления.
Метрологические характеристики СИ
MX
Характеристики свойств СИ, влияющая на результат
измерений и на его погрешность.
Примечание:
МХ, устанавливаемые нормативно-техническими
документами, называют нормируемыми МХ (НМХ), а
определяемые экспериментально – действительными
МХ.
78.
МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИМХ СИ позволяют:
определять результаты измерений и рассчитывать
оценки характеристик инструментальной
составляющей погрешности измерения в реальных
условиях применения СИ;
рассчитывать MX каналов измерительных систем,
состоящих из ряда СИ с известными MX;
производить оптимальный выбор СИ, обеспечивающих
требуемое качество измерений при известных
условиях их применения;
сравнивать СИ, различных типов с учетом условий
применения.
79.
МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИВ полном перечне установленных MX можно выделить
следующие группы:
градуировочные характеристики, определяющие
соотношение между сигналами на входе и выходе СИ в
статическом режиме;
показатели точности СИ, позволяющие оценить
инструментальную составляющую погрешности
результата измерения;
динамические характеристики, отражающие
инерционные свойства СИ и необходимые для
оценивания динамических погрешностей результатов
измерений.
80.
МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИДиапазон измерения
Область значений измеряемой величины, для которой
нормированы допускаемые пределы погрешности СИ
(для преобразователей – это диапазон преобразования).
Предел измерения
Наибольшее или наименьшее значение диапазона
измерения (для мер – это номинальное значение
воспроизводимой величины).
Цена деления шкалы
Разность значений величин, соответствующих двум
соседним отметкам шкалы.
Приборы с равномерной шкалой имеют постоянную цену
деления, а с неравномерной – переменную.
81.
МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИЧувствительность
Отношение изменения сигнала Δу на выходе СИ к
вызвавшему это изменение изменению Δx сигнала на
входе:
Δy
S=
Δx
Например, для стрелочного СИ – это отношение
перемещения dl конца стрелки к вызвавшему его
изменению dx измеряемой величины:
dl
S=
dx
82.
МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИОсновная MX СИ:
Погрешность СИ
Разность между показанием средства измерений и
истинным (действительным) значением измеряемой
физической величины.
Примечания:
Для меры показанием является ее номинальное
значение.
Поскольку истинное значение физической величины
неизвестно, то на практике пользуются ее
действительным значением.
Все погрешности СИ в зависимости от внешних
условий делятся на основные и дополнительные.
83.
МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИОсновная погрешность СИ
Погрешность СИ, применяемого в нормальных условиях
эксплуатации.
Примечание:
Как правило, нормальными условиями эксплуатации
являются:
температура (293 ± 5) К или (20±5) °С,
относительная влажность воздуха (65 ± 15) % при
20 °С,
напряжение в сети питания 220 В ± 10% с частотой
50 Гц ± 1%,
атмосферное давление от 97,4 кПа до 104 кПа,
отсутствие электрических и магнитных полей
(наводок).
84.
МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИДополнительная погрешность СИ
Составляющая погрешности СИ, возникающая
дополнительно к основной погрешности вследствие
отклонения какой-либо из влияющих величин от
нормального ее значения или вследствие ее выхода за
пределы нормальной области значений.
85.
МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИВ качестве предела допускаемой погрешности выступает
наибольшая погрешность, вызываемая изменением
влияющей величины, при которой СИ по техническим
требованиям может быть допущено к применению. То же
самое относится и к дополнительным погрешностям.
При этом исходят из следующих положений:
дополнительная погрешность имеет такой же вид, что
и основная (абсолютная, относительная и
приведенная);
дополнительные погрешности, вызванные
различными влияющими факторами, должны
нормироваться раздельно.
86.
МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИВ общем виде суммарная абсолютная погрешность СИ
при влияющих факторах определяется в виде:
n
ΔΣ = Δ0 + Δi 2 ,
i=1
где Δ0 – основная погрешность СИ;
Δi – дополнительная погрешность, вызванная
изменением i-го влияющего фактора.
Вследствие сложности разделения дополнительных и
основных погрешностей поверку СИ выполняют только
при нормальных условиях (т.е. дополнительные
погрешности исключены).
87.
88.
МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИСистематическая погрешность СИ
Составляющая погрешности средства измерений,
принимаемая за постоянную или закономерную
изменяющуюся.
Примечание:
Систематическая погрешность данного средства
измерений, как правило, будет отличаться от
систематической погрешности другого экземпляра
средства измерений этого же типа, вследствие чего для
группы однотипных средств измерений
систематическая погрешность может иногда
рассматриваться как случайная погрешность.
89.
МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИСлучайная погрешность СИ
Составляющая погрешности средства измерений,
изменяющаяся случайным образом.
Статическая погрешность
Погрешность средства измерений, применяемого при
измерении физической величины, принимаемой за
неизменную.
Динамическая погрешность
Погрешность средства измерений, возникающая при
измерении изменяющейся (в процессе измерений)
физической величины.
90.
МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИВ соответствии с ГОСТ 8.401–80 «ГСИ. Классы точности
средств измерений. Общие требования»
для пределов допускаемой основной (и дополнительной)
погрешностей предусмотрены различные способы
выражения в виде абсолютной, относительной и
приведенной погрешности:
Абсолютная погрешность СИ
Погрешность средства измерений, выраженная в
единицах измеряемой физической величины
Δ = |x – хд|.
В качестве хд выступает либо номинальное значение
(например, меры), либо значение величины, измеренной
более точным (не менее чем на порядок, в 10 раз) СИ.
91.
МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИАбсолютная погрешность выражается в единицах
измеряемой физической величины и может быть задана:
либо одним числом (линия 1): Δ = ±а;
либо в виде линейной зависимости (линии 2 и 3):
Δ = ± bx; Δ = ±(а+bx);
в виде функции Δ = f(x) или графика, таблицы.
92.
МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИЕсли значение погрешности
не изменяется во всем
диапазоне измерения (линия
1), например, из-за трения в
опорах, то такая погрешность
называется аддитивной (или
погрешностью нуля).
Если погрешность изменяется пропорционально
измеряемой величине (линия 2), то ее называют
мультипликативной.
В большинстве случаев аддитивная и мультипликативная
составляющие присутствуют одновременно (линия 3).
93.
МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИОтносительная погрешность
Погрешность СИ, выраженная отношением абсолютной
погрешности СИ к результату измерений или к
действительному значению измеренной ФВ.
Δ
Δ
δ = ± ⋅ 100% или δ = ± ⋅ 100%.
x
хд
Эта формула показывает, что для одного и того же СИ δ
уменьшается с ростом хд и приближается к ∞ при хд→0.
То есть, при измерении на начальном участке шкалы с
начальной нулевой отметкой погрешности измерения
могут быть сколь угодно велики.
Поэтому в метрологии существует принцип запрета
измерений на таких участках шкалы СИ.
94.
МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИУказание только абсолютной погрешности не позволяет
сравнивать между собой по точности СИ с разным пределом
измерений, а указание относительной погрешности также
ограничено из-за непостоянства величины δ. Поэтому
получило большое распространение нормирование
приведенной погрешности:
Приведенная погрешность
Относительная погрешность, выраженная отношением
абсолютной погрешности средства измерений к условно
принятому значению величины (нормирующему
значению), постоянному во всем диапазоне измерений
или в части диапазона:
Δ
γ = ± ⋅ 100%.
хн
95.
МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИПриведенная погрешность
Нормирующее значение хн принимается равным:
конечному значению рабочей части шкалы, если
нулевая отметка – на краю или вне рабочей части
шкалы;
сумме конечных значений шкалы (без учета знака),
если нулевая отметка – внутри шкалы;
длине шкалы, если она существенно неравномерна
(поскольку длина выражается в мм, то абсолютную
погрешность надо выражать также в мм);
номинальному значению х, если СИ предназначено
для измерения отклонения измеряемой величины
от номинального значения.
96.
МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИТакже нормированию подлежат:
Характеристики систематической составляющей
погрешности СИ;
Изменения значения МХ, вызванные изменением
влияющих величин;
Характеристики случайной составляющей
погрешности;
Функции влияния;
Изменения значений MX, вызванные изменениями
влияющих величин;
Неинформативные параметры выходного сигнала и др.
97.
КЛАССЫ ТОЧНОСТИ СИПриведенная в ГОСТ 8.009–84 «ГСИ. Нормируемые
метрологические характеристики средств измерений»
номенклатура MX в известном смысле предполагает
строгое нормирование MX СИ, используемых при
высокоточных лабораторных измерениях и
метрологической аттестации, других СИ.
При технических измерениях, когда не предусмотрено
выделение случайных и систематических составляющих,
когда не существенна динамическая погрешность СИ,
когда не учитываются влияющие (дестабилизирующие)
факторы и т.д., можно пользоваться более грубым
нормированием – присвоением СИ определенного класса
точности по ГОСТ 8.401–80 «ГСИ. Классы точности
средств измерений. Общие требования».
































































































 mathematics
mathematics








