Similar presentations:
Алгоритмы и структуры данных
1.
2-3-дерево и другиеАлгоритмы и структуры данных
Лекция
2.
Содержание лекции2-3-дерево
В-дерево
АА-дерево
сравнение АВЛ-дерева, красно-черного
дерева, 2-3-дерева и АА-дерева.
3.
2-3-дерево2-3-дерево — структура данных, являющаяся B-деревом , которая может
содержать только 2-вершины (вершины с одним полем и 2 детьми) и 3вершины (вершины с 2 полями и 3 детьми). Листовые вершины являются
исключением — у них нет детей (но может быть одно или два поля).
2-3-деревья сбалансированы, то есть, каждое левое, правое, и центральное
поддерево имеет одну и ту же высоту, и, таким образом, содержат равные
(или почти равные) объемы данных.
В 2-вершине поле больше любого элемента левого поддерева и меньше
любого элемента правого поддерева.
В 3-вершине первое поле больше любого элемента левого поддерева и
меньше любого элемента центрального поддерева, а второе поле больше
любого элемента центрального поддерева и меньше любого элемента
правого поддерева.
4.
2-3-деревоСвойства 2-3-дерева.
1.Узел дерева может содержать
15
один или два ключа.
2.Узел может быть либо листом
(не имеет поддеревьев), либо
4 10
18
иметь 2 непустых поддерева
(если в узле один ключ), либо
иметь 3 непустых поддерева
(если в узле два ключа).
6 9
20 23
1
12
16
3.Все листья 2-3-дерева
находятся на одном и том же
уровне.
Физически узел, содержащий два ключа, может быть представлен двумя
отдельными объектами, один из которых специальным образом помечен.
4
10
4
10
5.
2-3-деревоВысота дерева не может быть больше, чем log2N, где N –
количество ключей в дереве. В то же время, при поиске в
дереве по ключу, в каждом узле может производиться одно
или два сравнения. Так что общее число сравнений при поиске
не может превышать 2 log2N.
Алгоритм поиска будет почти таким же, как и в случае
обычного бинарного дерева поиска, с поправкой на то, что в
узле может быть 2 ключа.
6.
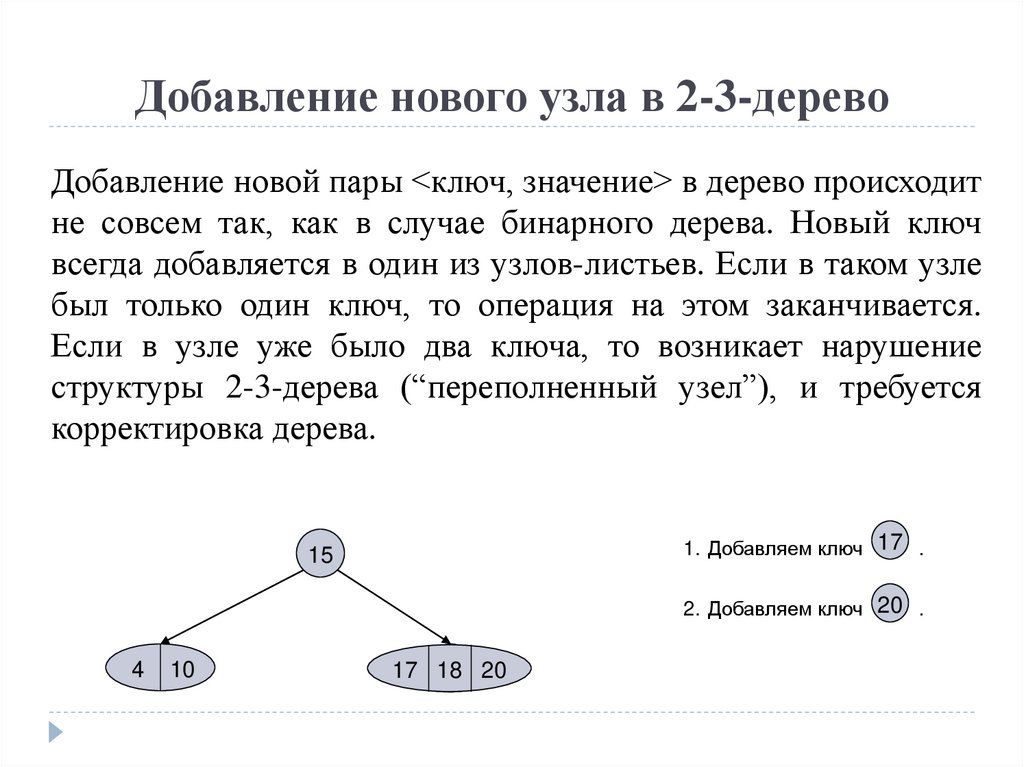
Добавление нового узла в 2-3-деревоДобавление новой пары <ключ, значение> в дерево происходит
не совсем так, как в случае бинарного дерева. Новый ключ
всегда добавляется в один из узлов-листьев. Если в таком узле
был только один ключ, то операция на этом заканчивается.
Если в узле уже было два ключа, то возникает нарушение
структуры 2-3-дерева (“переполненный узел”), и требуется
корректировка дерева.
1. Добавляем ключ 17 .
15
2. Добавляем ключ 20 .
4
10
1717181820
7.
Корректировка 2-3-дерева после добавлениянового ключа
Есть два вида преобразования дерева, которое можно сделать при наличии
“переполненного” ключа: переливание и расщепление. Переливание возможно только в том
случае, когда у данного переполненного узла имеется соседний брат, содержащий только
один ключ. Расщепление возможно выполнить всегда, но оно может вызвать появление
переполненного узла на предыдущем (меньшем по номеру) уровне.
5
Переливание
Расщепление
77 13
12
10
10 15
101012
13 1515 1818
6
8
13
13 15 1818
Если после проведения расщепления узел, находящийся на предыдущем уровне,
оказывается переполненным, то надо для него провести расщепление или
переливание. Для корня дерева переливание невозможно, а при расщеплении
образуется новый корень дерева.
8.
Примеры преобразования дерева придобавлении узла
14
15
12
2 2 9 9 12
1
4
6
15 1919
10 12
12 14
14
10
18
22
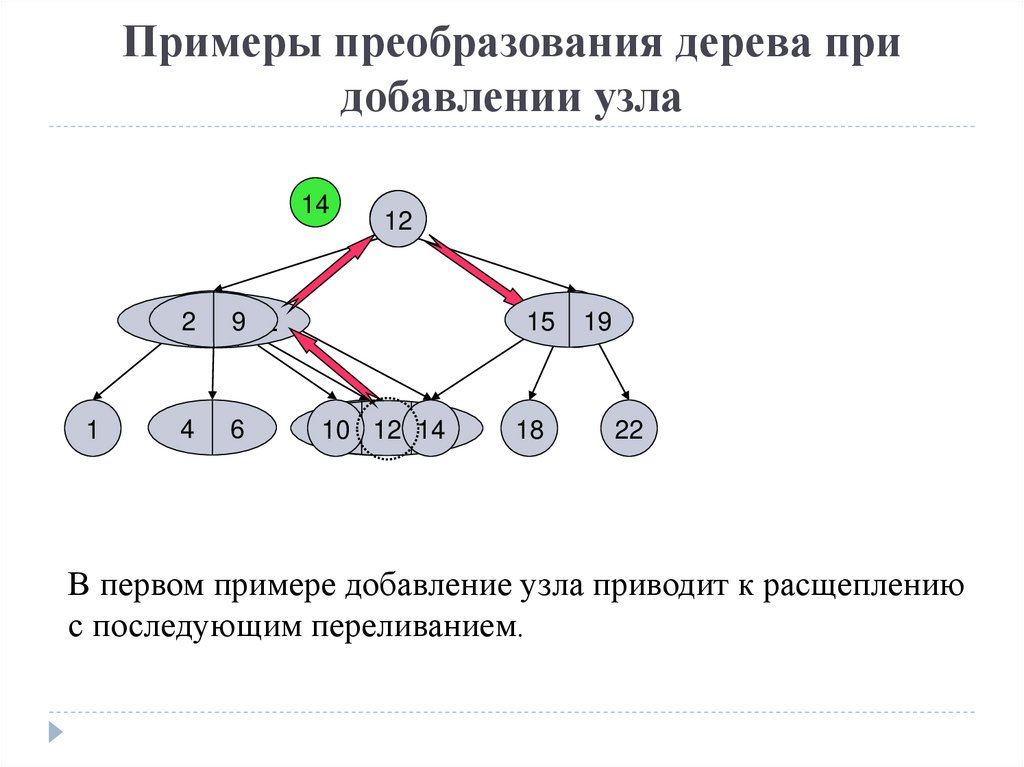
В первом примере добавление узла приводит к расщеплению
с последующим переливанием.
9.
Примеры преобразования дерева придобавлении узла
18
14
10
10 14
4 10
14
1
6
8
33 33
10 18
18 33
23
1212141515
20
25
28
37
30
36
40
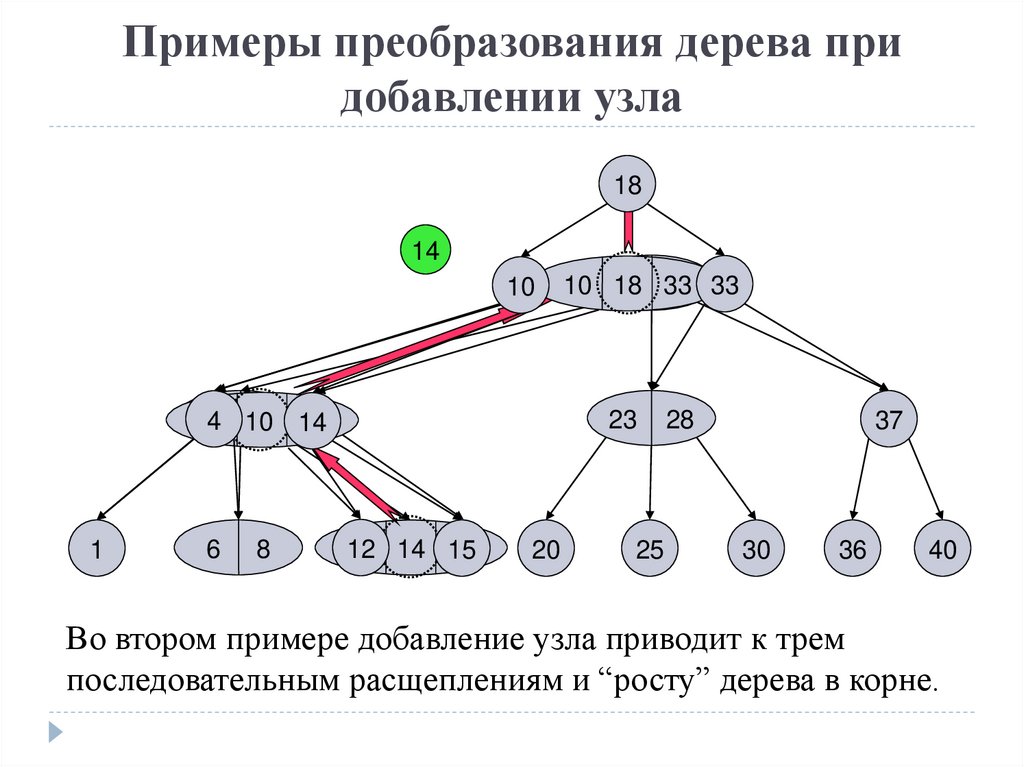
Во втором примере добавление узла приводит к трем
последовательным расщеплениям и “росту” дерева в корне.
10.
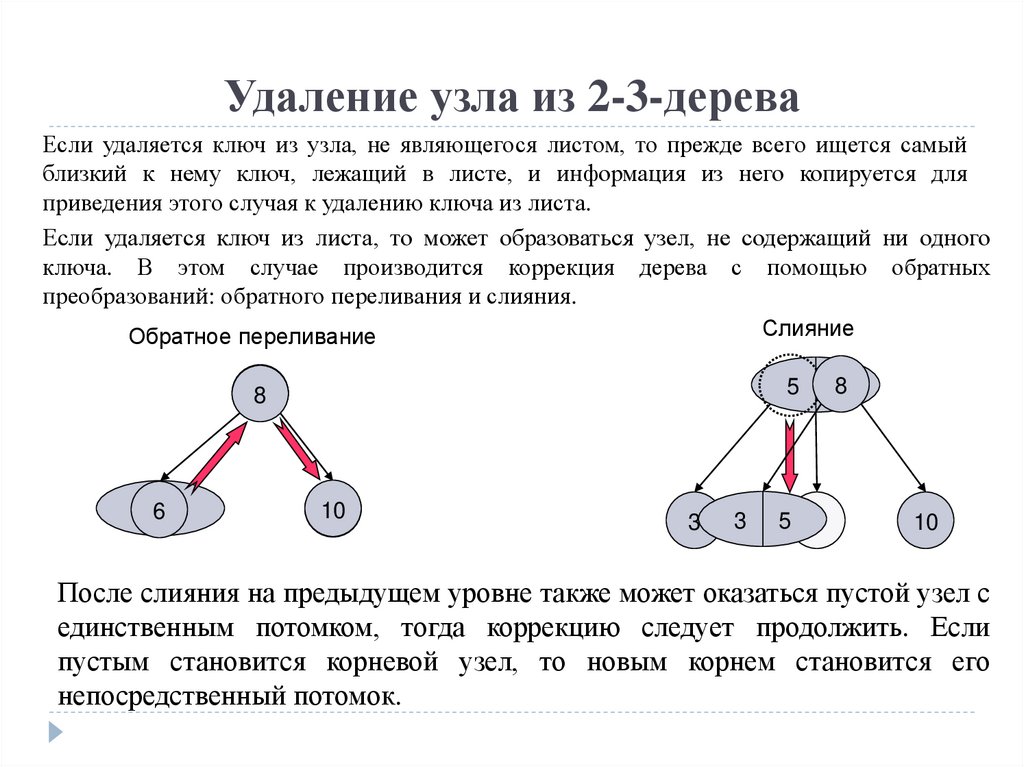
Удаление узла из 2-3-дереваЕсли удаляется ключ из узла, не являющегося листом, то прежде всего ищется самый
близкий к нему ключ, лежащий в листе, и информация из него копируется для
приведения этого случая к удалению ключа из листа.
Если удаляется ключ из листа, то может образоваться узел, не содержащий ни одного
ключа. В этом случае производится коррекция дерева с помощью обратных
преобразований: обратного переливания и слияния.
Обратное переливание
Слияние
10
8
5
66 8
10
3
3
5
88
10
После слияния на предыдущем уровне также может оказаться пустой узел с
единственным потомком, тогда коррекцию следует продолжить. Если
пустым становится корневой узел, то новым корнем становится его
непосредственный потомок.
11.
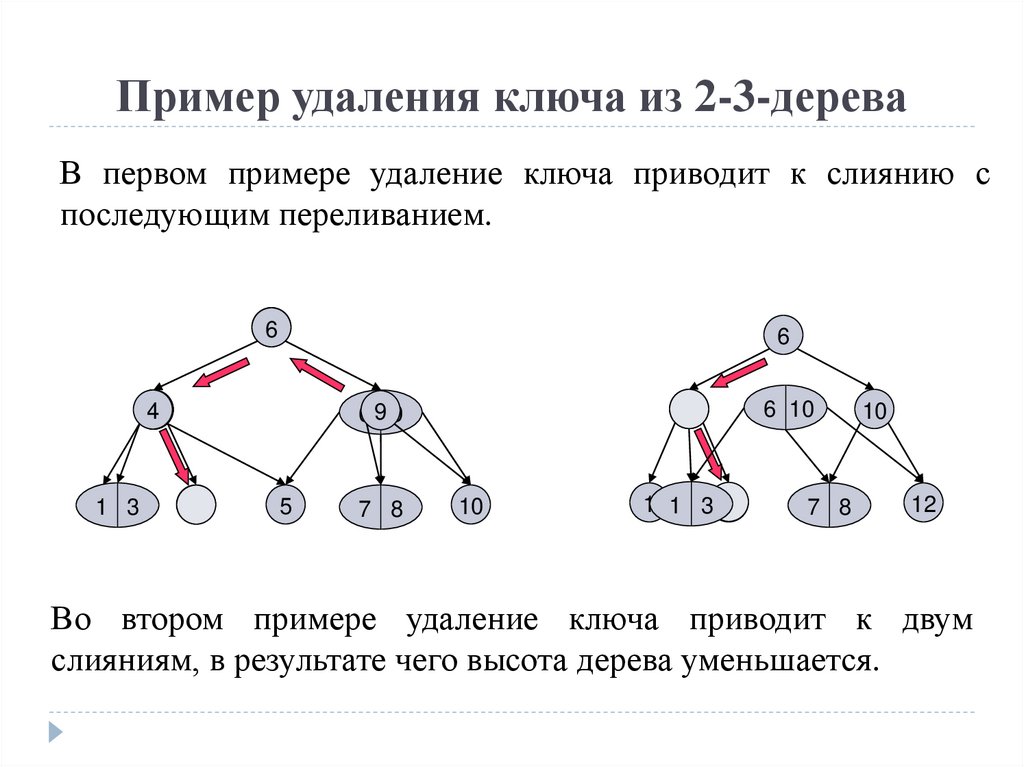
Пример удаления ключа из 2-3-дереваВ первом примере удаление ключа приводит к слиянию с
последующим переливанием.
4
6
6
4
2
3
1 3
3
699
3
5
7 8
10
1 1 35
6 10
7 8
10
12
Во втором примере удаление ключа приводит к двум
слияниям, в результате чего высота дерева уменьшается.
12.
Обобщение 2-3-дерева –В-дерево k-го порядка
13.
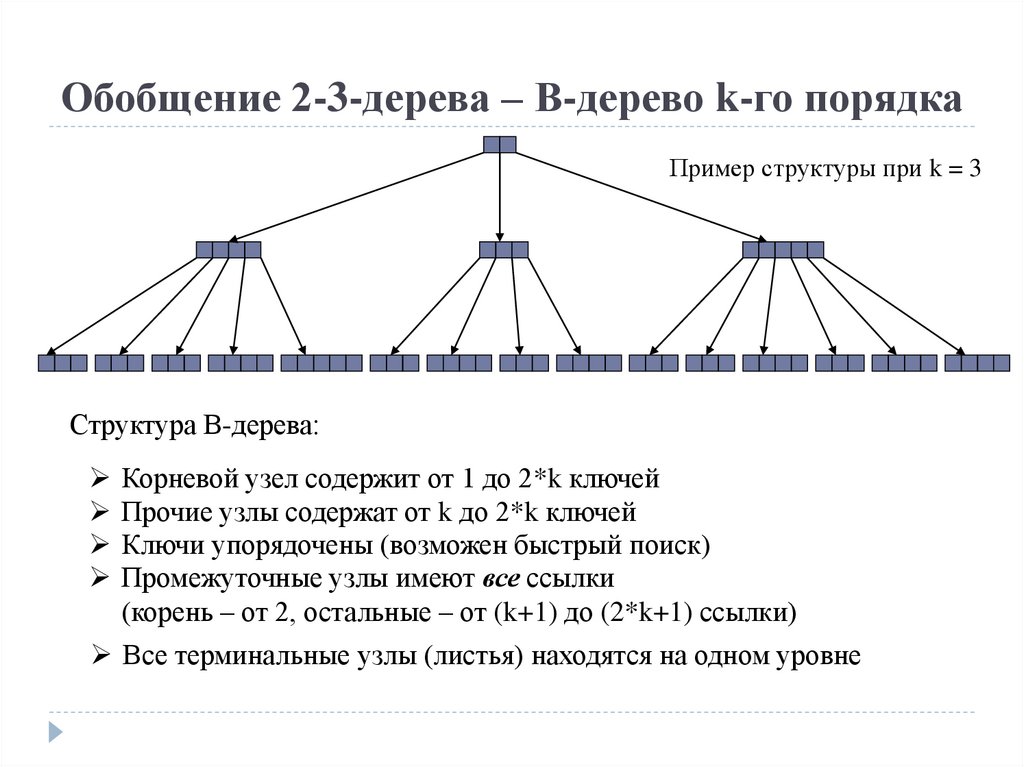
Обобщение 2-3-дерева – В-дерево k-го порядкаПример структуры при k = 3
Структура В-дерева:
Корневой узел содержит от 1 до 2*k ключей
Прочие узлы содержат от k до 2*k ключей
Ключи упорядочены (возможен быстрый поиск)
Промежуточные узлы имеют все ссылки
(корень – от 2, остальные – от (k+1) до (2*k+1) ссылки)
Все терминальные узлы (листья) находятся на одном уровне
14.
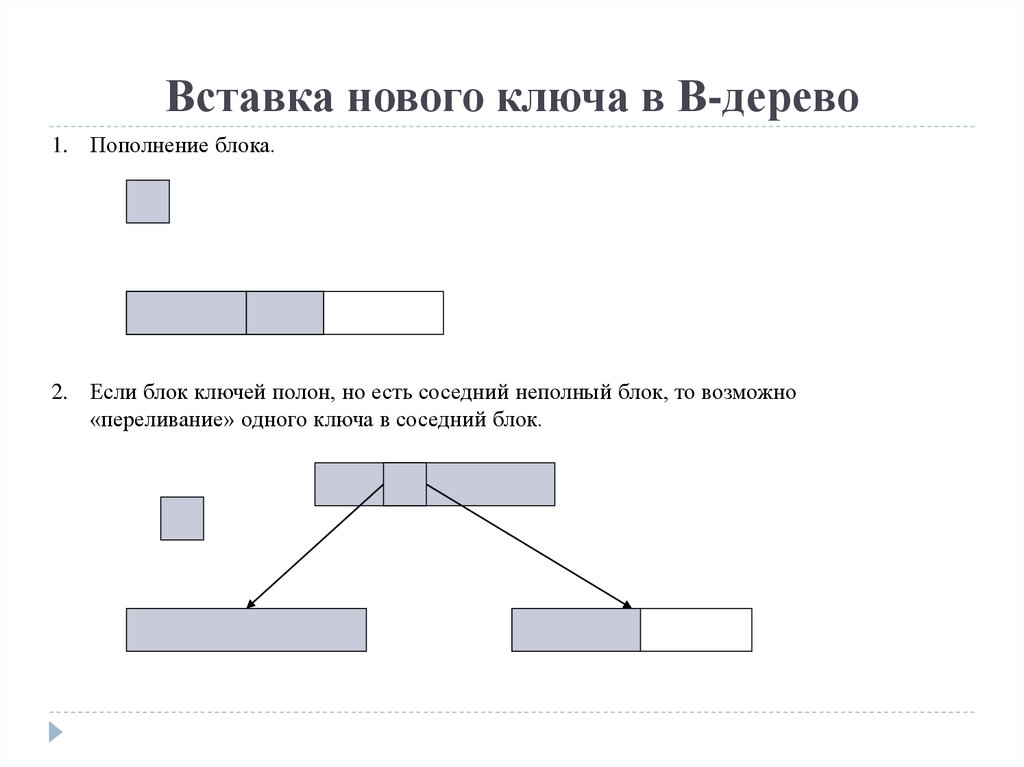
Вставка нового ключа в В-дерево1. Пополнение блока.
n < 2k ключей
2. Если блок ключей полон, но есть соседний неполный блок, то возможно
«переливание» одного ключа в соседний блок.
15.
Вставка нового ключа в В-дерево расщеплением узла3. Если блок ключей полон, и соседние с ним блоки тоже полны, то необходимо
делать расщепление блока.
k кл.
(2 * k +11) ключ
k кл.
При вставке ключа в терминальный узел образовалось переполнение узла
Делим узел на 3 узла: k, 1 и k ключей
Перемещаем средний ключ на предыдущий уровень
При расщеплении терминального узла, возможно, придется добавлять в
нетерминальные узлы ключи вместе с поддеревьями. При этом опять
возможно сделать это путем пополнения блока, переливания и
расщепления.
16.
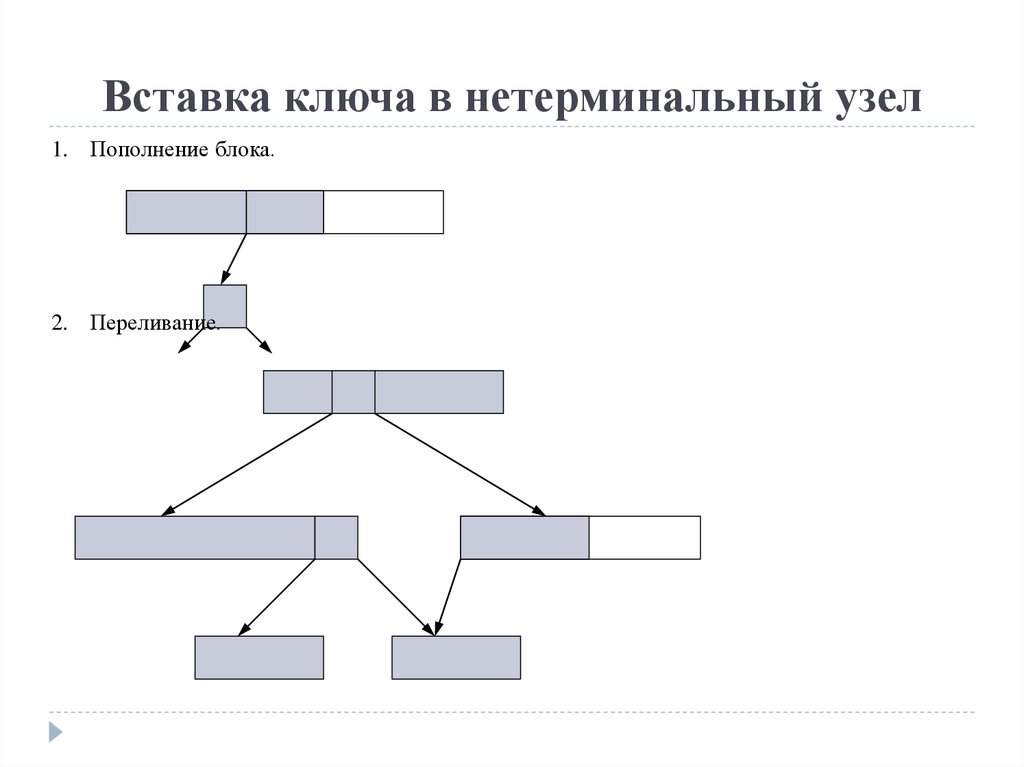
Вставка ключа в нетерминальный узел1. Пополнение блока.
n < 2k ключей
2. Переливание.
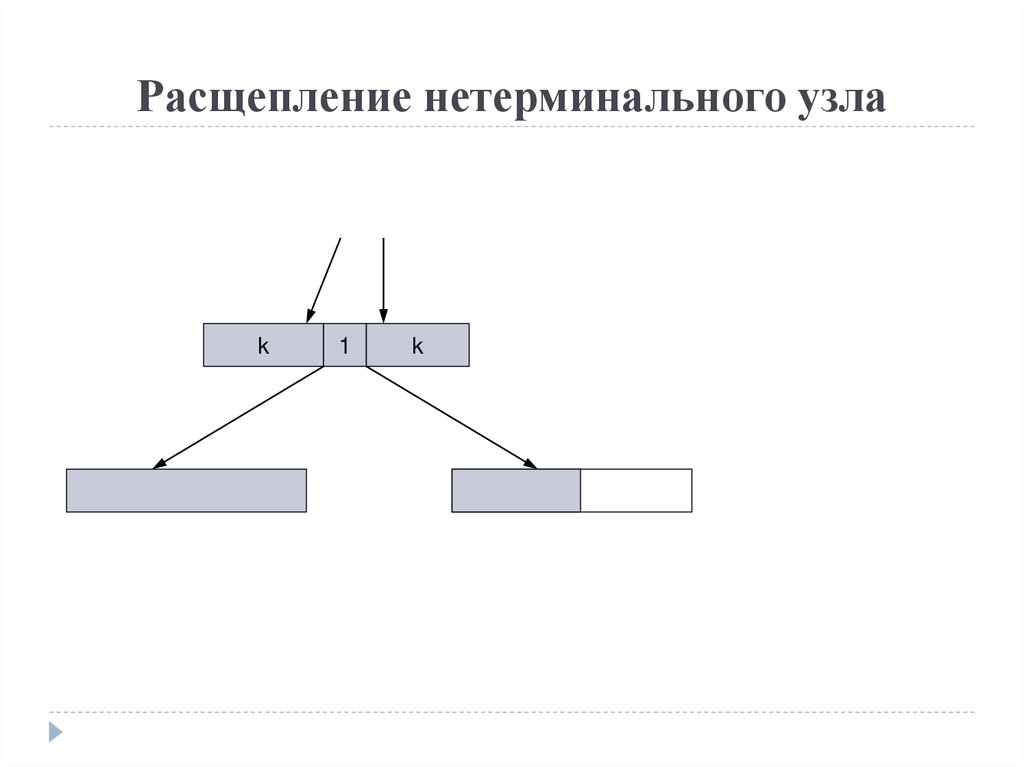
17.
Расщепление нетерминального узлаk
1
k
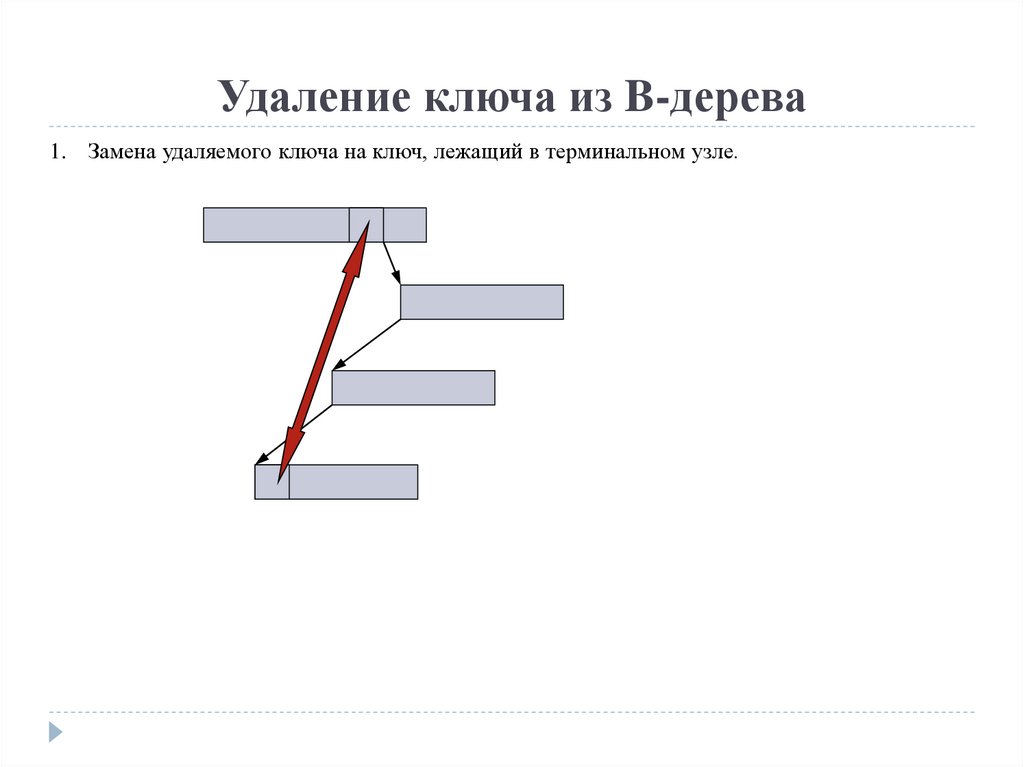
18.
Удаление ключа из B-дерева1. Замена удаляемого ключа на ключ, лежащий в терминальном узле.
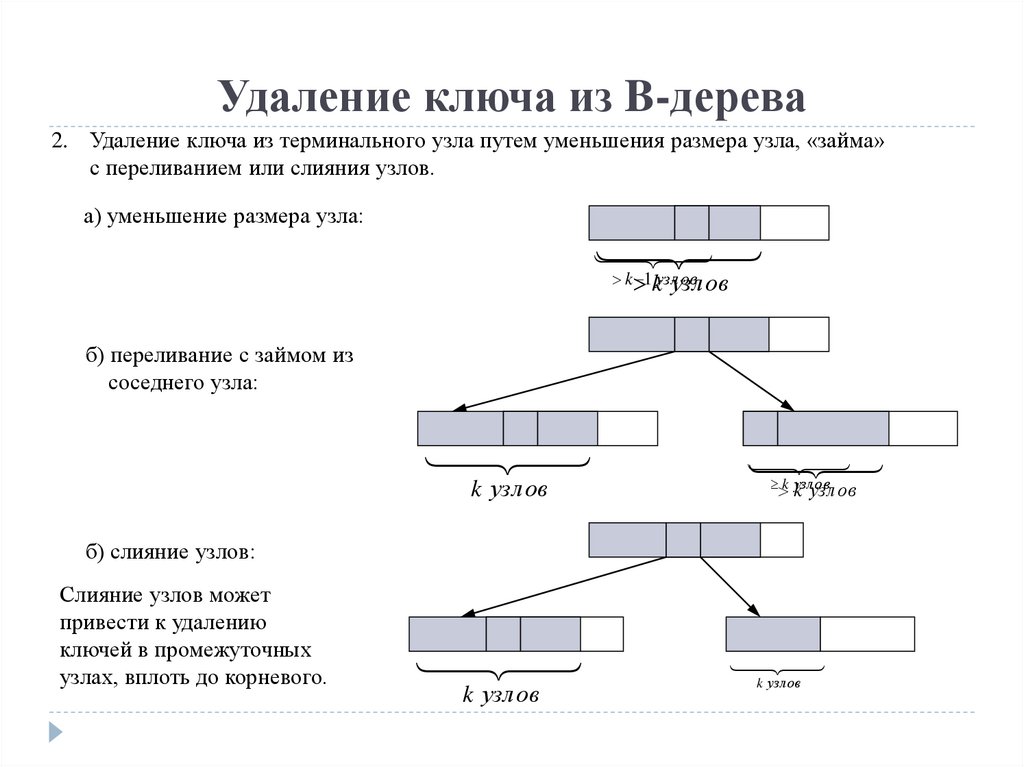
19.
Удаление ключа из B-дерева2. Удаление ключа из терминального узла путем уменьшения размера узла, «займа»
с переливанием или слияния узлов.
а) уменьшение размера узла:
k
1kузлов
узл ов
б) переливание с займом из
соседнего узла:
k узл ов
k узл ов
k узл ов
б) слияние узлов:
Слияние узлов может
привести к удалению
ключей в промежуточных
узлах, вплоть до корневого.
k узл ов
k узл ов
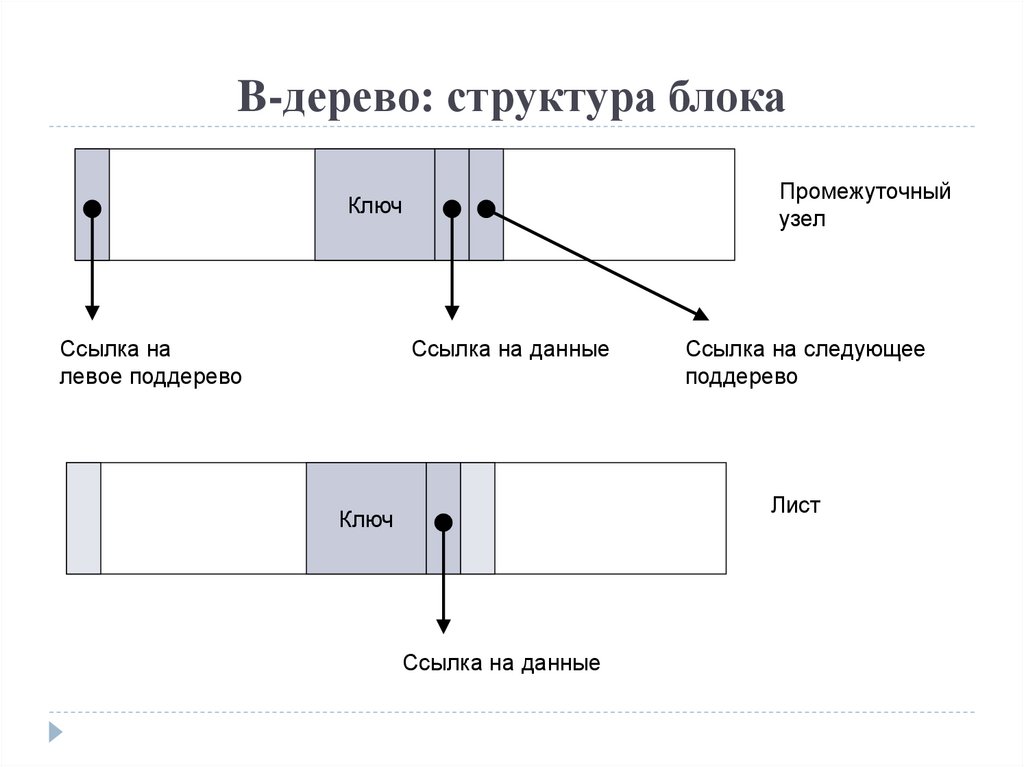
20.
B-дерево: структура блокаПромежуточный
узел
Ключ
Ссылка на
левое поддерево
Ссылка на данные
Ссылка на следующее
поддерево
Лист
Ключ
Ссылка на данные
21.
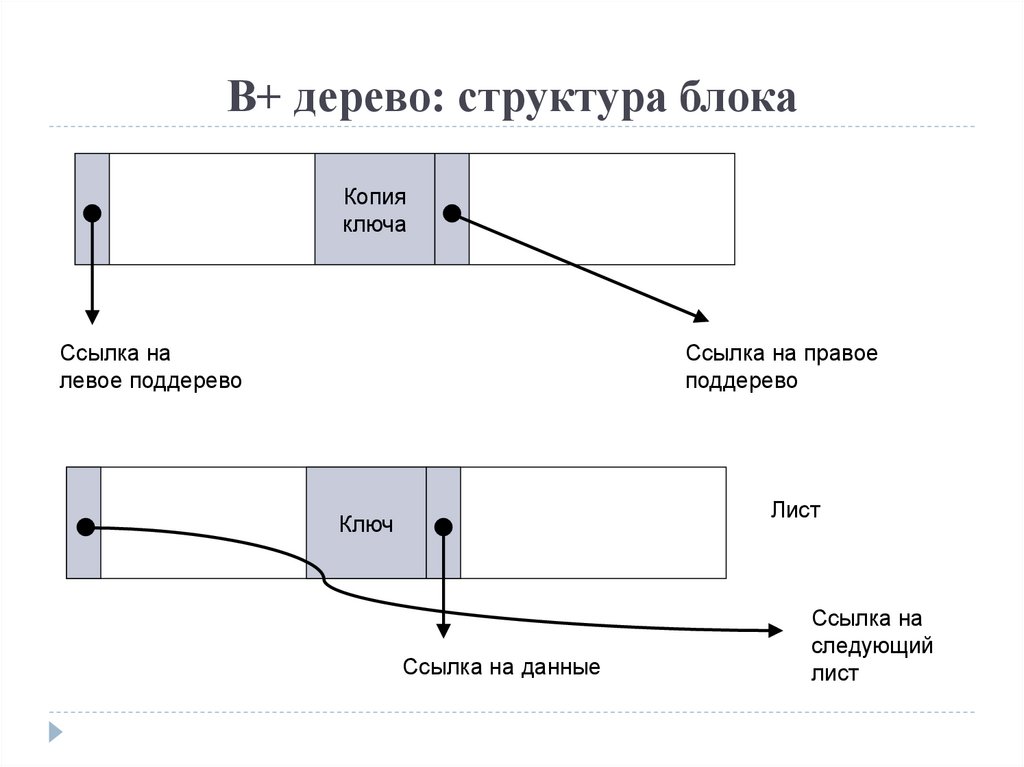
В+ дерево: структура блокаКопия
ключа
Ссылка на
левое поддерево
Ссылка на правое
поддерево
Лист
Ключ
Ссылка на данные
Ссылка на
следующий
лист
22.
Общая структура B+ дерева21 37
7 12
1 3 4 6
7 10
21 26
12 14
15 17 19
21 24
37 43
26 29
32 35
37 40 42
43 46
23.
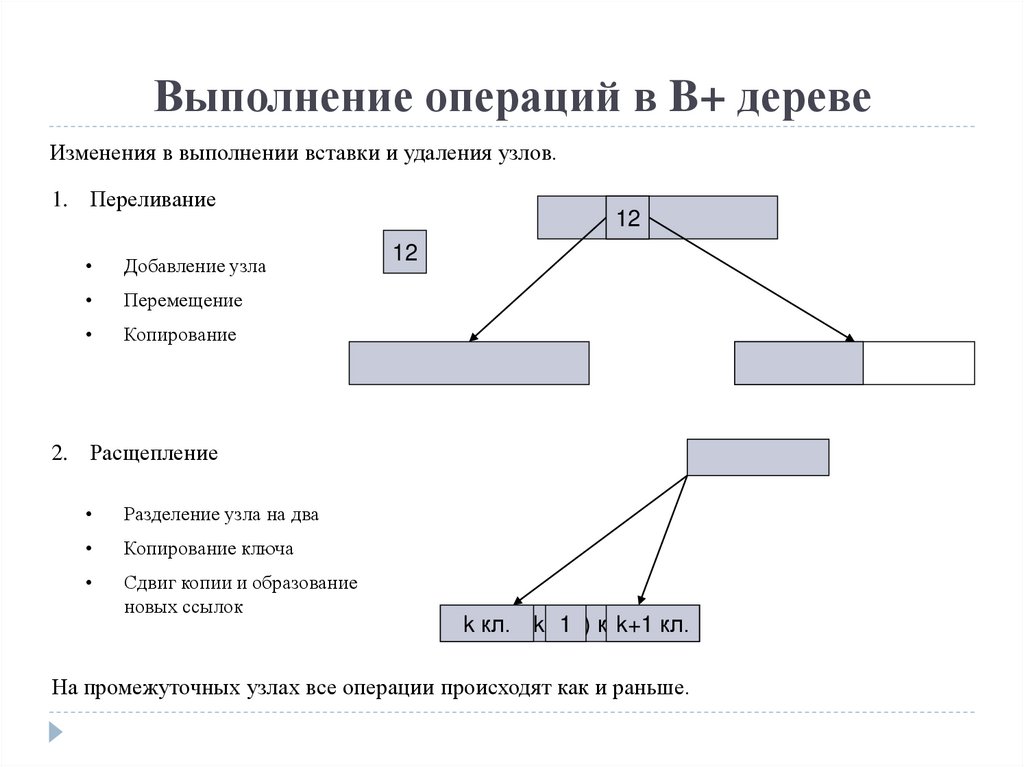
Выполнение операций в B+ деревеИзменения в выполнении вставки и удаления узлов.
1. Переливание
Добавление узла
Перемещение
Копирование
12
15
12
2. Расщепление
Разделение узла на два
Копирование ключа
Сдвиг копии и образование
новых ссылок
k кл.
(2 * k +11) ключ
k+1 кл.
На промежуточных узлах все операции происходят как и раньше.
24.
Особенности B+ дереваПри удалении ключей могут оставаться копии
удаленных ключей. Это никак не влияет на алгоритм и
результат поиска.
Преимущества структуры В+ дерева перед В деревом:
1. Унификация структуры узлов;
2. Наличие сквозного списка ключей позволяет легко
находить отрезки данных.
Некоторое усложнение работы операций по вставке
и удалению ключей влияет на общую скорость работы
незначительно, поскольку не связано с дополнительными
операциями чтения/записи данных.
25.
АА-деревья26.
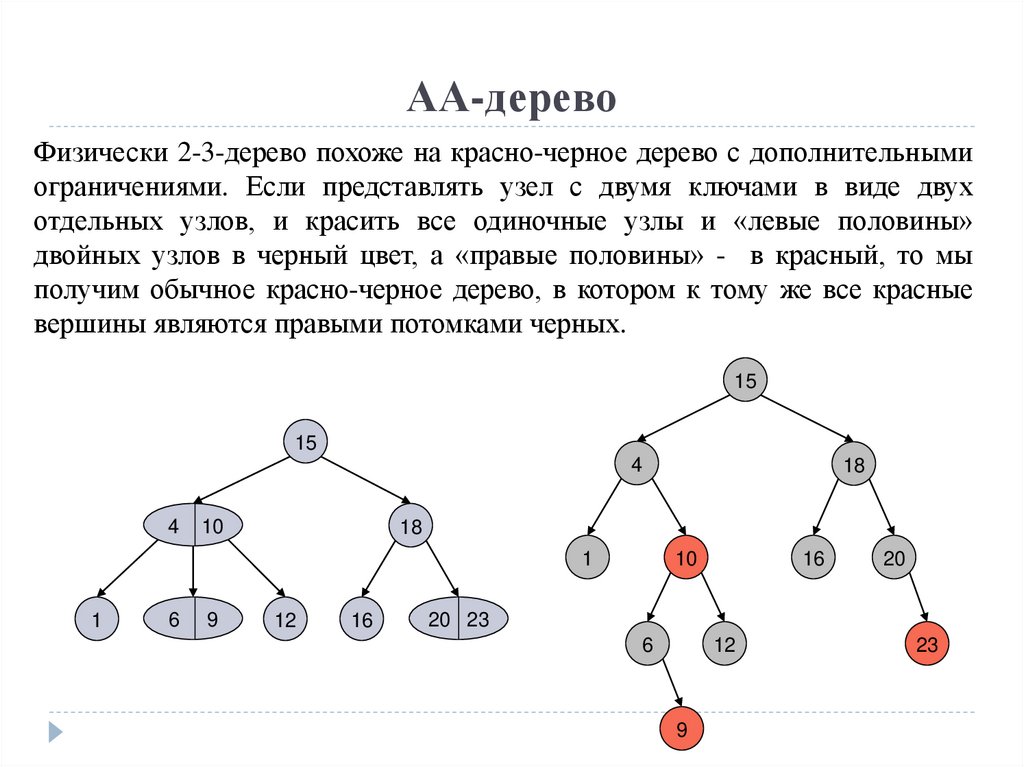
АА-деревоФизически 2-3-дерево похоже на красно-черное дерево с дополнительными
ограничениями. Если представлять узел с двумя ключами в виде двух
отдельных узлов, и красить все одиночные узлы и «левые половины»
двойных узлов в черный цвет, а «правые половины» - в красный, то мы
получим обычное красно-черное дерево, в котором к тому же все красные
вершины являются правыми потомками черных.
15
15
4
4
10
18
1
1
6
9
18
12
16
10
16
20
20 23
6
12
9
23
27.
Уровни узлов в АА-деревеВместо того, чтобы раскрашивать узлы в красный и черный цвета, введем
понятие уровня узла. Будем считать, что все листья дерева имеют уровень
1, а уровень родителя имеет уровень на единицу больший, чем уровень
потомка. В качестве исключения будем считать, что если потомок является
правым потомком, то его уровень может быть равен уровню родительского
узла.
ур. 3
15
15
4
1
ур. 2
18
10
6
16
12
9
4
10
6
9
18
ур. 1
20
1
23
12
16
20
23
28.
Структура АА-дереваБудем называть АА-деревом двоичное дерево поиска, узлы
которого содержат натуральное число, называемое уровнем
узла, и подчиняющееся следующим правилам:
1. Уровни всех листьев равны единице.
2. Уровень левого потомка на единицу меньше
уровня его родителя.
3. Уровень правого потомка равен или на единицу
меньше уровня его родителя.
4. Уровень потомка потомка (внука) всегда строго
меньше уровня предка его предка (дедушки).
5. Промежуточные узлы (не листья) всегда имеют
ровно двух потомков.
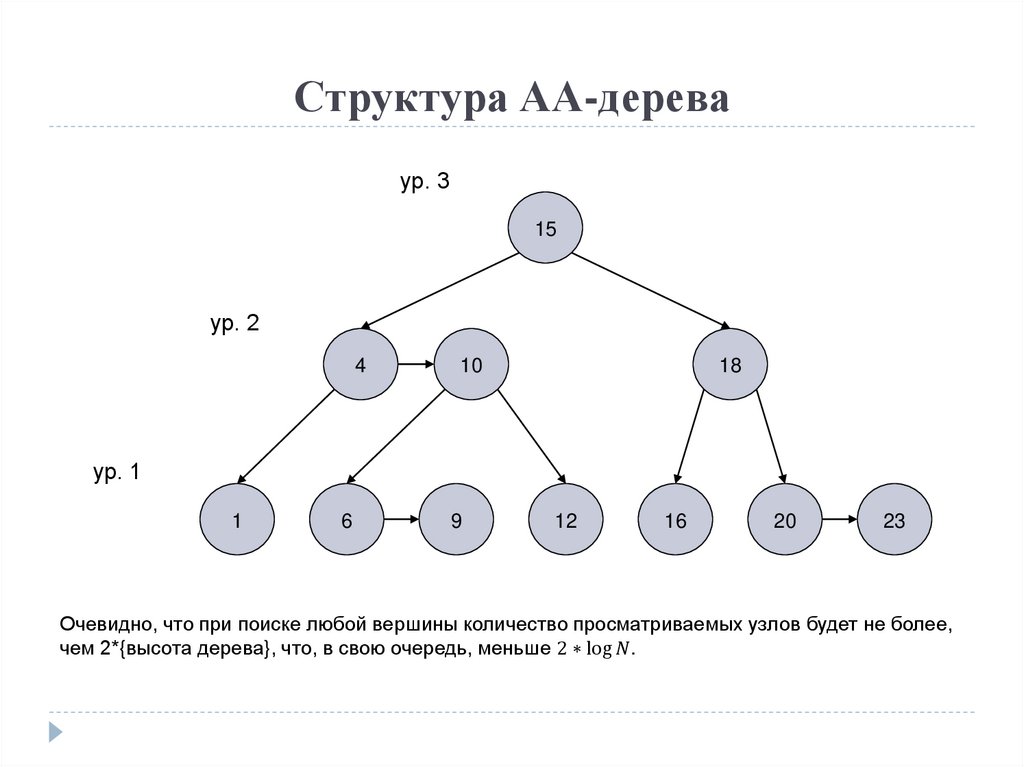
29.
Структура АА-дереваур. 3
15
ур. 2
4
10
18
ур. 1
1
6
9
12
16
20
23
Очевидно, что при поиске любой вершины количество просматриваемых узлов будет не более,
чем 2*{высота дерева}, что, в свою очередь, меньше 2 ∗ log















 programming
programming








