Similar presentations:
Динамика и прочность конструкций. Лекция 1
1.
Черник Денис Владимирович2.
ВведениеДинамические нагрузки на машины
и механизмы характеризуются
настолько быстрым изменением во
времени их величины, направления или
места приложения, что вызывают
колебания конструкций, которые
необходимо учитывать при расчёте.
Таковы нагрузки, возникающие при
работе машин с неуравновешенными
движущимися массами, при ударах
массивных тел, при землетрясениях и
взрывах и т.д.
3.
Колебательный характер имеют нетолько перемещения точек сооружения,
но и внутренние усилия и напряжения в
конструктивных элементах. Определение
ожидаемых амплитуд перемещений,
внутренних усилий и напряжений в
механизме при его колебаниях под
действием динамической нагрузки и
сравнение их с допустимыми значениями
составляют основное содержание
динамического расчёта.
4.
Допустимые значения амплитудвнутренних усилий обусловлены
требованиями прочности и
долговечности конструкций, а значения
амплитуд скоростей и ускорений
колебаний элементов конструкций, в
которых находятся люди или, —
требованиями безвредного влияния
колебаний на здоровье людей и на
качество выпускаемой продукции.
5.
Уметь рассчитать колебанияразличных объектов машиностроения,
приборостроения, транспортной и
строительной техники, правильно
оценить их воздействие на изучаемые
системы, экспериментально исследовать
параметры колебаний и должным
образом толковать результаты
наблюдений – необходимые качества
современного квалифицированного
выпускника инженерных
специальностей.
6.
Целью изучения дисциплины" Динамика и прочность конструкций "
является ознакомление с возможными
видами движений в линейных
динамических системах, особенностями
их развития и установления,
характеристиками как стационарных, так
и нестационарных процессов, анализ
идеализированных математических
моделей исследуемых систем.
7.
Изучение дисциплинынаправлено на развитие навыков
решения проектноконструкторских;
производственнотехнологических; научноисследовательских задач.
8.
Лекция 1 Предмет динамики. Основные задачи.Основное уравнение динамики. Колебательное
движение механической системы.
План
1. Введение. Предмет динамики. Основные
задачи.
2. Основное уравнение динамики.
Колебательное движение механической
системы.
9.
1. Предмет динамики. Основные задачи.Динамикой называется раздел механики,
в котором изучается движение
материальных тел в зависимости от
действующих на них сил.
Динамика представляет собой наиболее
общий раздел механики, имеющий
особое значение для решения многих
практических задач в различных
областях техники.
10.
Динамический анализ используетсядля определения действия на
конструкцию или ее составные части
нагрузок, зависящих от времени. В
отличие от статических расчетов в
этом типе анализа принимается во
внимание рассеяние энергии и
инерционные эффекты переменных
во времени нагрузок. Примерами
таких нагрузок являются:
11.
циклические нагрузки(вращающиеся части оборудования);
внезапно приложенные нагрузки
(удар или взрыв);
случайные нагрузки
(землетрясение);
любые другие переменные нагрузки.
12.
Задачи, связанные с колебаниями,играют важнейшую роль в современной
инженерной механике. Только
динамические расчеты позволяют
досконально изучить целый ряд
прикладных проблем: колебания
турбинных лопаток и дисков,
балансировку вращающихся валов и
роторов, колебания зубчатых передач,
мостов, фундаментов и т.п.
13.
Колебания классифицируются по ряду признаков:по способу возбуждения различают свободные
колебания, вынужденные, параметрические и
автоколебания;
по виду деформаций, возникающих в элементах
колеблющейся системы; в частности,
применительно к стержневым системам
рассматриваются продольные, поперечные
(изгибные) и крутильные колебания;
в соответствии с законом, по которому величина,
характеризующая колебательный процесс,
изменяется во времени, различают периодические и
непериодические колебания.
14.
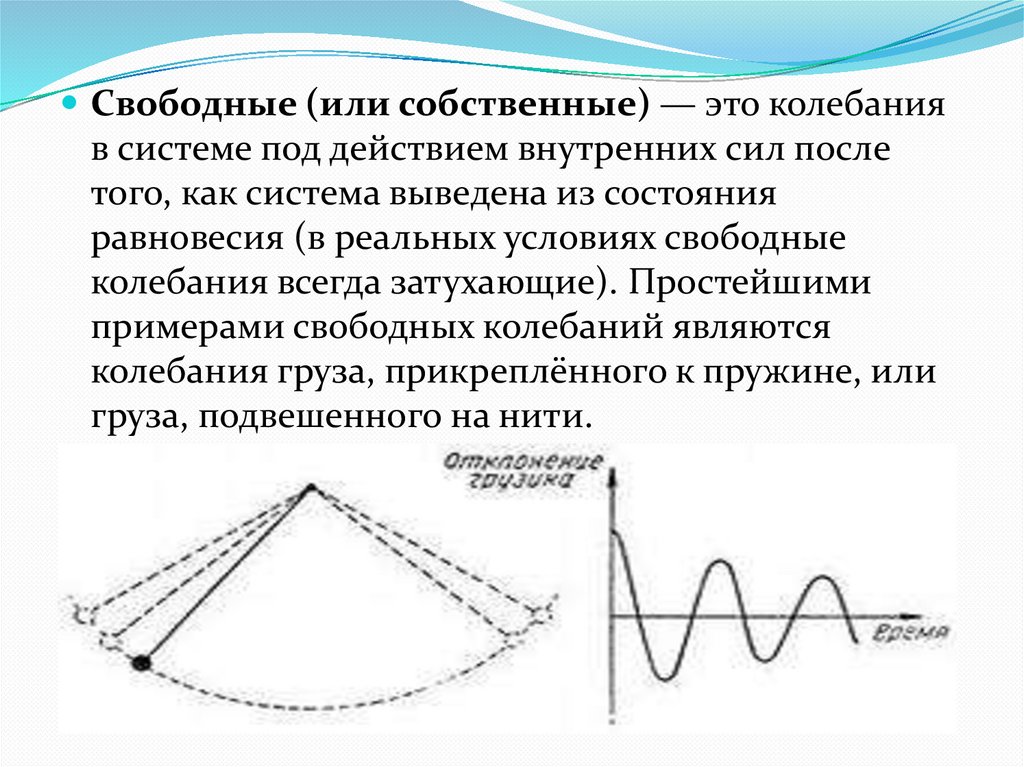
Свободные (или собственные) — это колебанияв системе под действием внутренних сил после
того, как система выведена из состояния
равновесия (в реальных условиях свободные
колебания всегда затухающие). Простейшими
примерами свободных колебаний являются
колебания груза, прикреплённого к пружине, или
груза, подвешенного на нити.
15.
Вынужденные — колебания, протекающие всистеме под влиянием внешнего периодического
воздействия. Примеры: листья на деревьях,
поднятие и опускание руки. При вынужденных
колебаниях может возникнуть явление резонанса:
резкое возрастание амплитуды колебаний при
совпадении собственной частоты осциллятора и
частоты внешнего воздействия.
16.
Параметрические — колебания, возникающиепри изменении какого-либо параметра
колебательной системы в результате внешнего
воздействия.
Автоколебания — колебания, при которых
система имеет запас потенциальной энергии,
расходующейся на совершение колебаний (пример
такой системы — механические часы).
Характерным отличием автоколебаний от
вынужденных колебаний является то, что их
амплитуда определяется свойствами самой
системы, а не начальными условиями.
17.
Простые продольные колебания – это процессраспространения в пространстве областей сжатий
и растяжений среды. Сжатия и растяжения среды
образуются при колебаниях ее точек (частиц)
около своих положений равновесия.
18.
Крутильные колебания - механическиеколебания, при которых упругие элементы
испытывают деформации сдвига. Имеют место в
различных машинах с вращающимися валами: в
поршневых двигателях, турбинах, генераторах,
редукторах, трансмиссиях транспортных машин.
19.
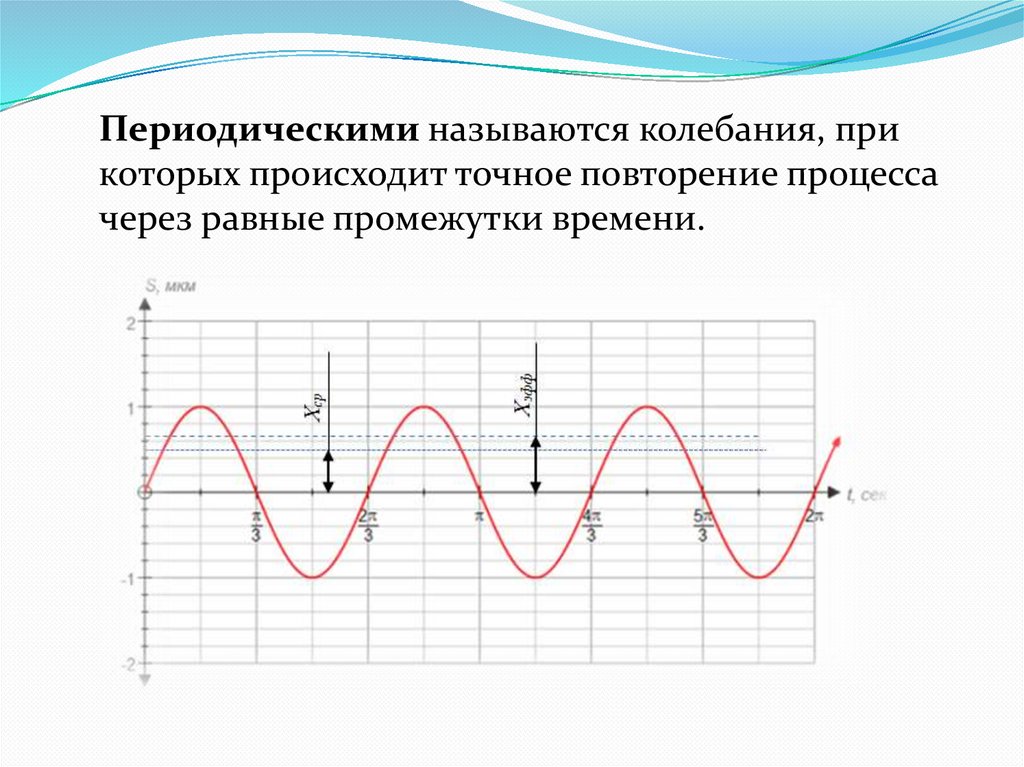
Периодическими называются колебания, прикоторых происходит точное повторение процесса
через равные промежутки времени.
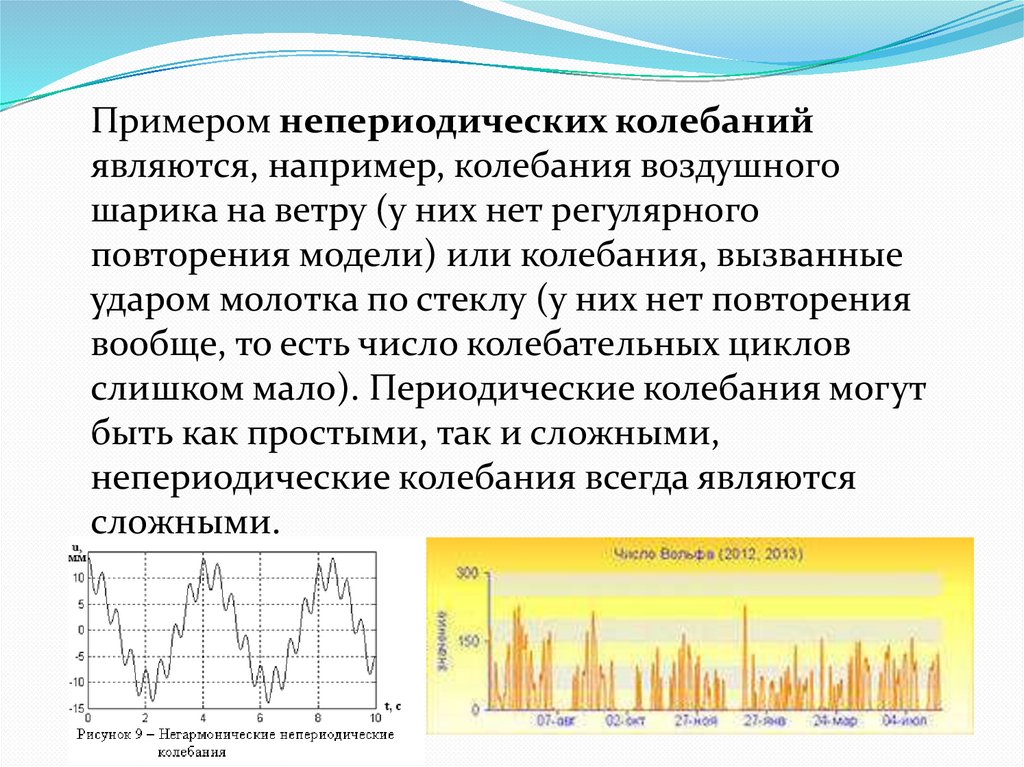
20.
Примером непериодических колебанийявляются, например, колебания воздушного
шарика на ветру (у них нет регулярного
повторения модели) или колебания, вызванные
ударом молотка по стеклу (у них нет повторения
вообще, то есть число колебательных циклов
слишком мало). Периодические колебания могут
быть как простыми, так и сложными,
непериодические колебания всегда являются
сложными.
21.
Основные характеристики механическихколебаний
Основными характеристиками механических
колебаний являются: амплитуда, частота, период,
фаза колебаний.
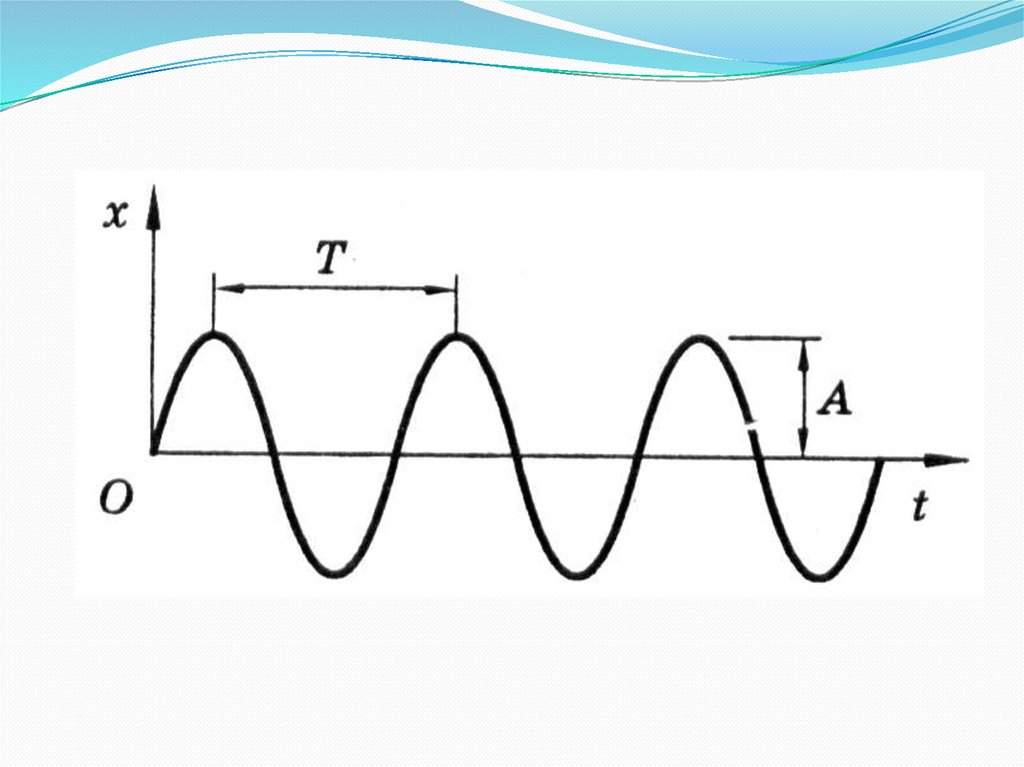
Амплитуда колебаний (А) - наибольшее
отклонение колеблющегося тела от положения
равновесия (отклонение величины от ее среднего
значения);
Период колебаний (Т) - время, через которое
движение тела полностью повторяется (повторяются
все кинематические характеристики колебаний), т.е.
совершается одно полное колебание;
22.
23.
Частота колебаний (ν) – величина, показываю-щая число колебаний, совершаемых за 1 с.
n
1
t
T
[Гц],
где n – число колебаний
t – время, с.
Вместо частоты (ν) чаще пользуются понятием
циклической частоты (ω).
Циклическая (или круговая) частота (ω) – это
число полных колебаний, совершаемых за
промежуток времени, равный 2π секунд.
2
[рад/с]
2
T
24.
Фаза колебаний - это величина, котораяопределяет положение колебательной системы в
любой момент времени. Обозначается φ.
Измеряется в радианах.
Пример: если два шарика на нитях одинаковой
длины отвести от положения равновесия вправо и
отпустить, то они будут колебаться в фазе
(синфазно, синхронно), если их развести в разные
стороны, то колебания будут происходить в
противофазе.
25.
В свою очередь все колеблющиеся системыподразделяются на системы с одной степенью
свободы, с конечным числом степеней свободы
и с бесконечным (иначе — системы с
распределенными параметрами). Любая
реальная механическая система состоит из
бесконечного числа материальных точек, связи
между которыми не являются абсолютно
жесткими, поэтому число степеней свободы
реальной механической системы бесконечно
велико.
26.
Для решения задач динамики применяются дваосновных способа:
статический, основанный на применении уравнений
динамического равновесия, которые отличаются от
уравнений статического равновесия дополнительным
учетом (согласно принципу Даламбера) сил инерции в
виде произведения масс или их моментов инерции на
ускорения;
энергетический, основанный на применении закона
сохранения энергии, согласно которому сумма
потенциальной и кинетической энергии упругой
системы есть величина постоянная.
Трудоемкость динамического расчета той или
иной системы зависит прежде всего от ее числа
степеней свободы
27.
2. Основное уравнение динамики.Колебательное движение систем
В основе динамики лежат три закона И. Ньютона,
из которых как следствия получаются все
уравнения и теоремы, необходимые для решения
задач динамики. Согласно первому закону
(закону инерции) материальная точка, на которую
не действуют силы, находится в состоянии покоя
или равномерного прямолинейного движения;
изменить это состояние может только действие
силы.
28.
Второй закон, являющийся основнымзаконом динамики, устанавливает, что
при действии силы F материальная точка
(или поступательно движущееся тело) с
массой m получает ускорение a,
определяемое равенством
ma=F
(1)
29.
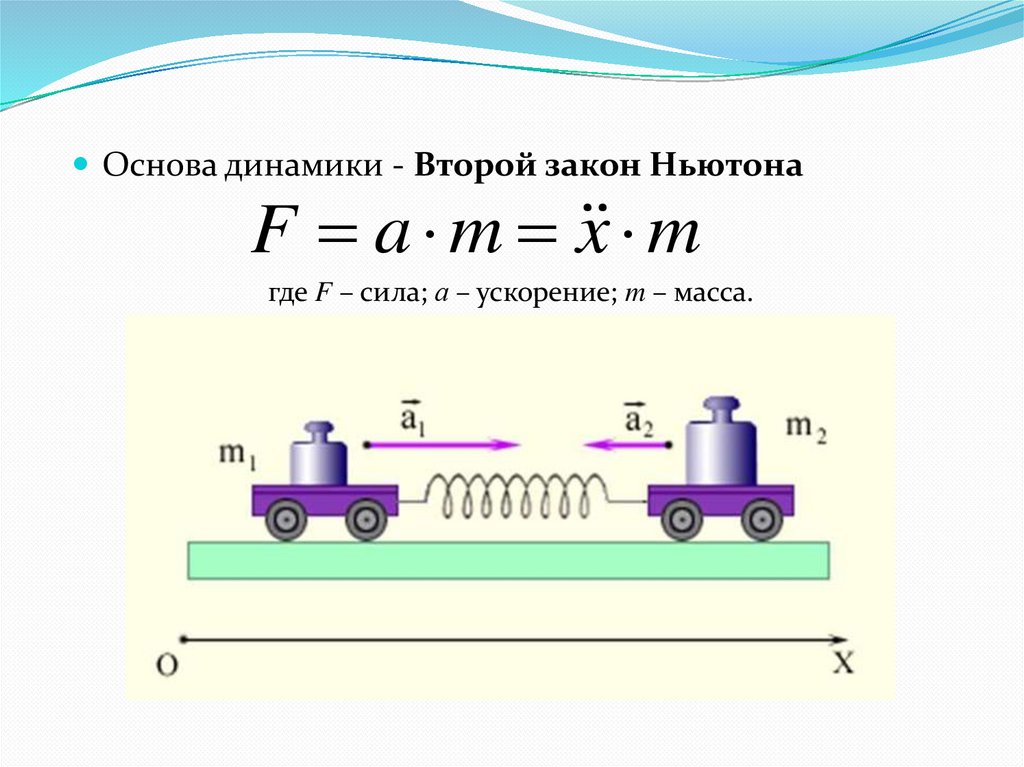
Основа динамики - Второй закон НьютонаF a m x m
где F – сила; а – ускорение; m – масса.
30.
Третьим законом является закон оравенстве действия и противодействия.
Когда к телу приложено несколько сил, F
в уравнении (1) означает их
равнодействующую. Этот результат
следует из закона независимости
действия сил, согласно которому при
действии на тело нескольких сил каждая
из них сообщает телу такое же ускорение,
какое она сообщила бы, если бы
действовала одна.
31.
Основа статики - третий закон Ньютона.сила действия равна по модулю и противоположна по
направлению силе противодействия.
32.
В динамике рассматриваются два типа задач,решения которых для материальной точки (или
поступательно движущегося тела) находятся с
помощью уравнения (1). Задачи первого типа
состоят в том, чтобы, зная движение тела,
определить действующие на него силы. В технике
такие задачи возникают при определении сил, с
которыми движущиеся тела действуют на связи, т.
е. др. тела, ограничивающие их движение,
например при определении сил давления колёс на
рельсы, а также при нахождении внутренних
усилий в различных деталях машин и механизмов,
когда законы движения этих машин (механизмов)
известны.
33.
Задачи второго типа, являющиеся в динамикеосновными, состоят в том, чтобы, зная
действующие на тело силы, определить закон
его движения. При решении этих задач
необходимо ещё знать так называемые
начальные условия, т. е. положение и скорость
тела в момент начала его движения под
действием заданных сил. Примеры таких задач:
зная силу упругости рессор и вес кузова вагона,
определить закон его колебаний, в частности
частоту этих колебаний, и многие др.




























 physics
physics mechanics
mechanics








