Similar presentations:
Стаціонарні випадкові процеси
1. Стаціонарні випадкові процеси
Підготував:Студент групи ПМ-3
Куценко Олександр
2. Стаціонарні випадкові процеси
Означення. Випадковий процес називається стаціонарним випадковим процесом, якщойого характеристики не змінюються зі зміною його аргументу, тобто, однакові у всіх
перетинах процесів X (t) і X (t + t0 ) , де t0 – будь-яке фіксоване число.
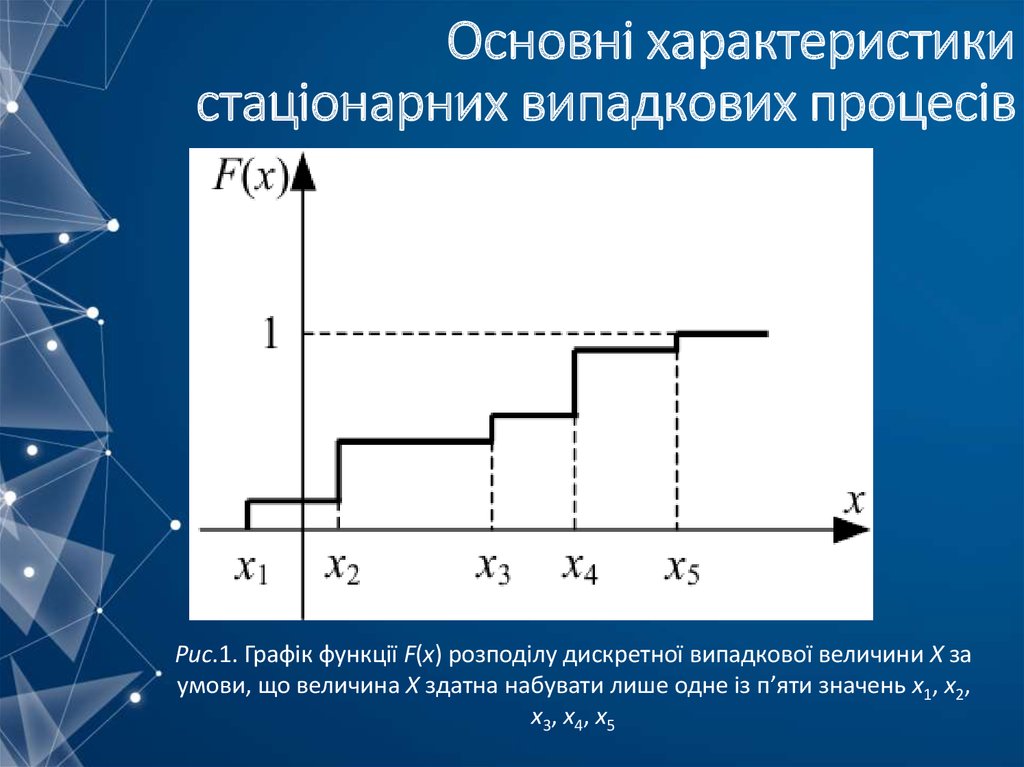
Означення. Випадкова функція X(t) називається стаціонарною, якщо всі її характеристики
імовірності не залежать від часу t, тобто
mx(t) = mx = const
Dx(t) = Dx = const
Отже, у стаціонарному процесі функції щільності ймовірностей не змінюються при заміні
аргументу t на t + t0 , тобто:
f(x1, x2, ... xn; t1, t2, ... tn) = f (x1, x2, ... xn; t1 + t0, t2 + t0, ... tn + t0)
де n =1, 2, ... , -∞ < t0 < +∞.
3. Стаціонарні випадкові процеси
Означення. Випадковий процесДля випадкових процесі, які є стаціонарними в
називається


















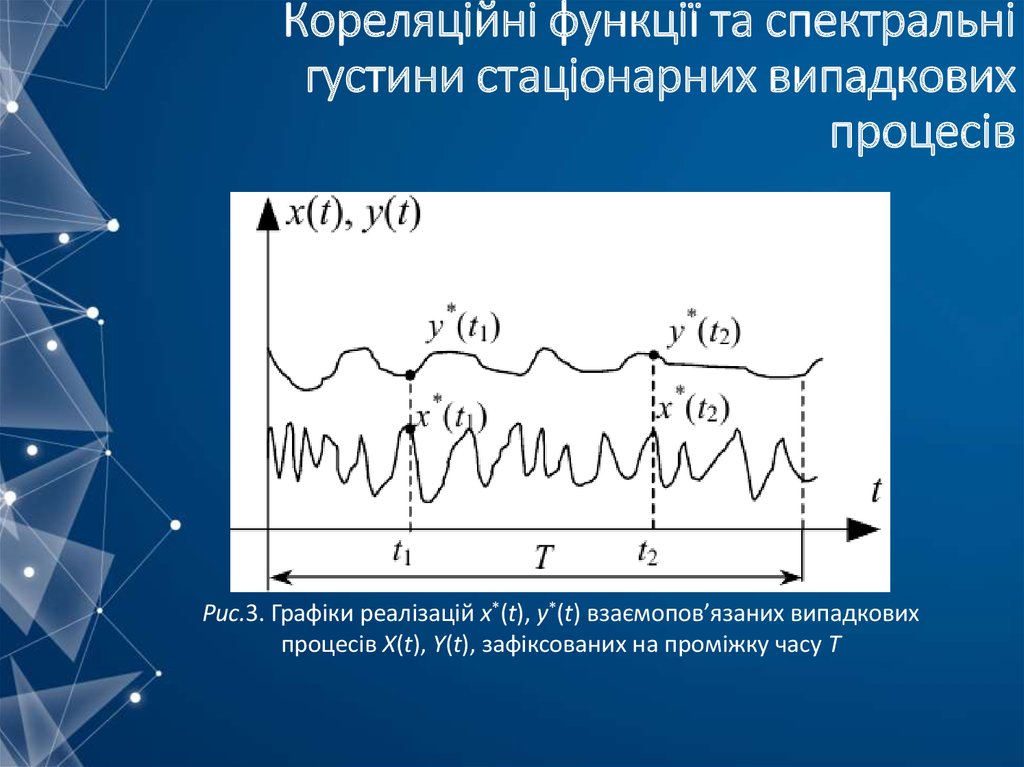

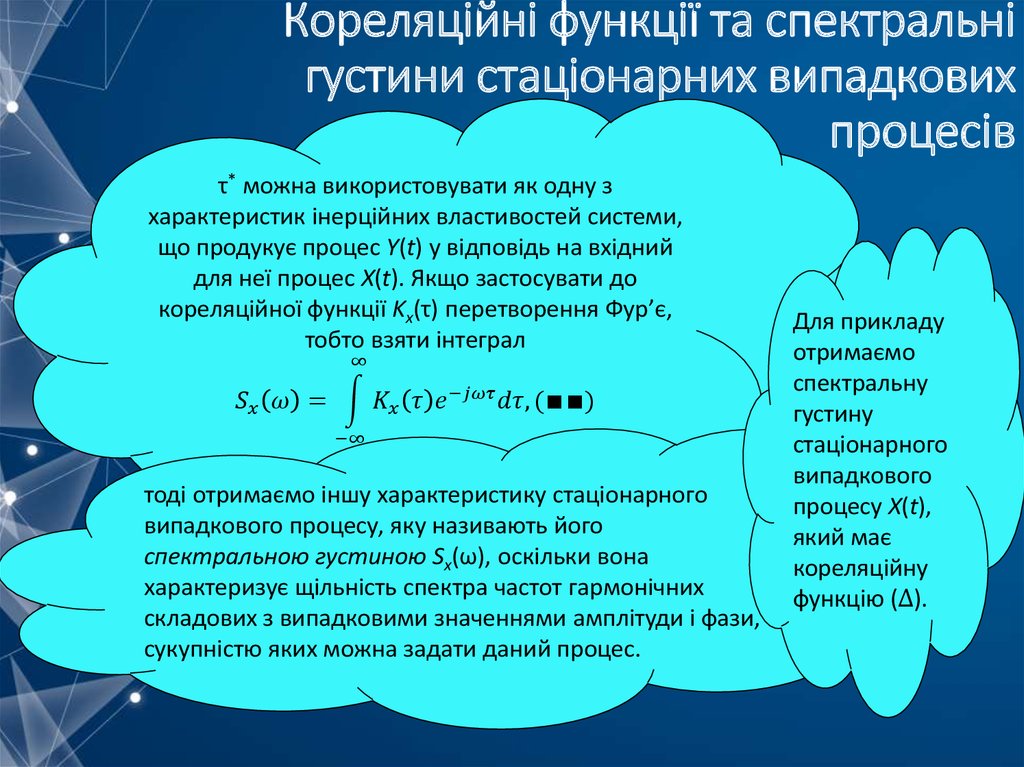
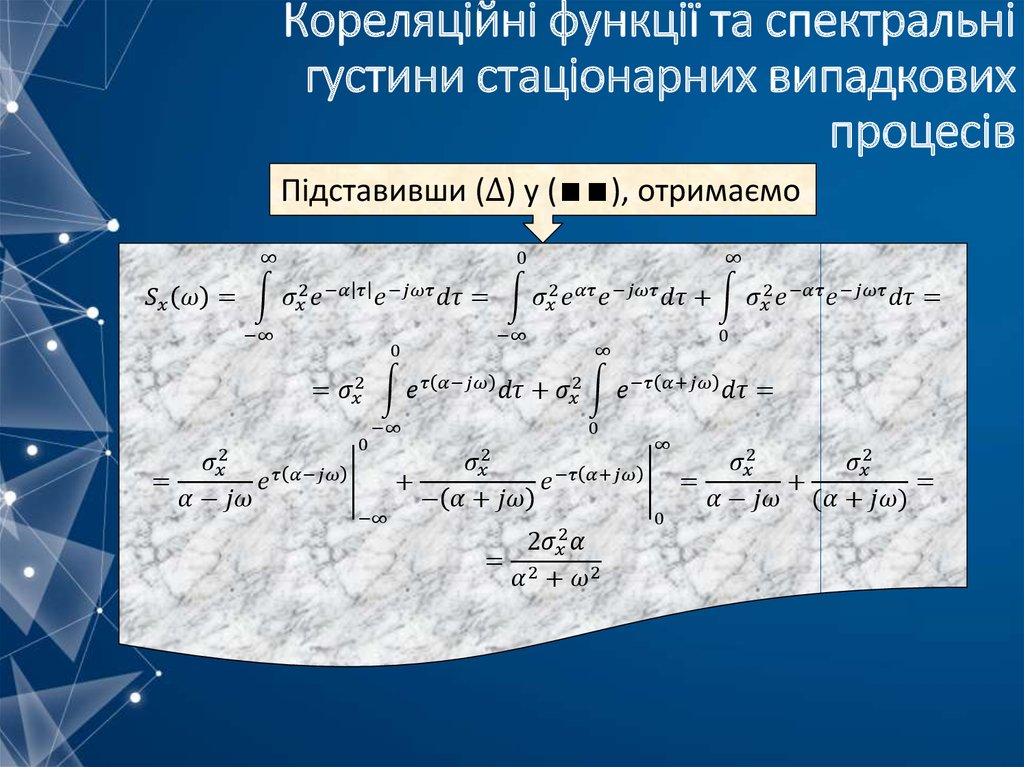
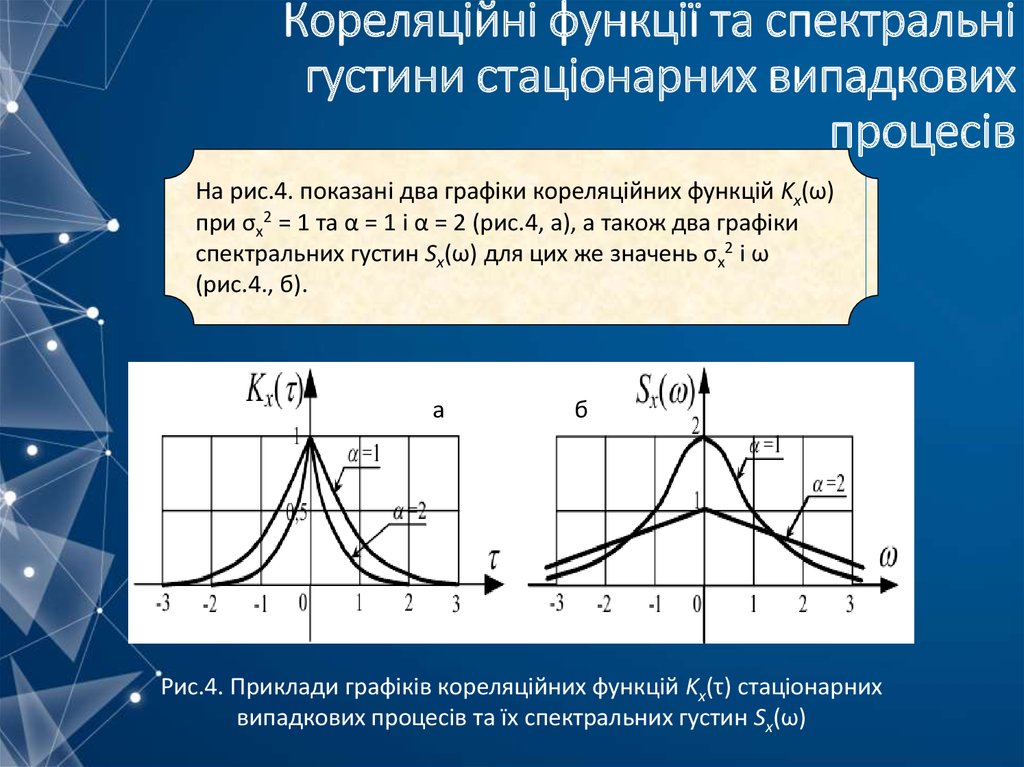
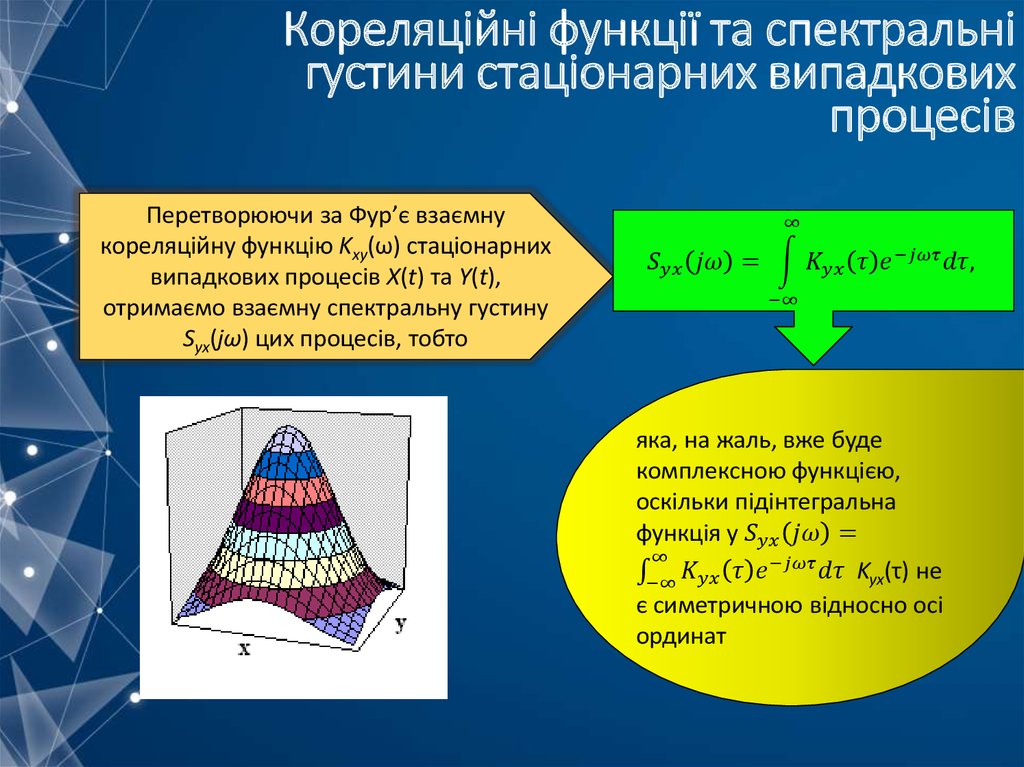



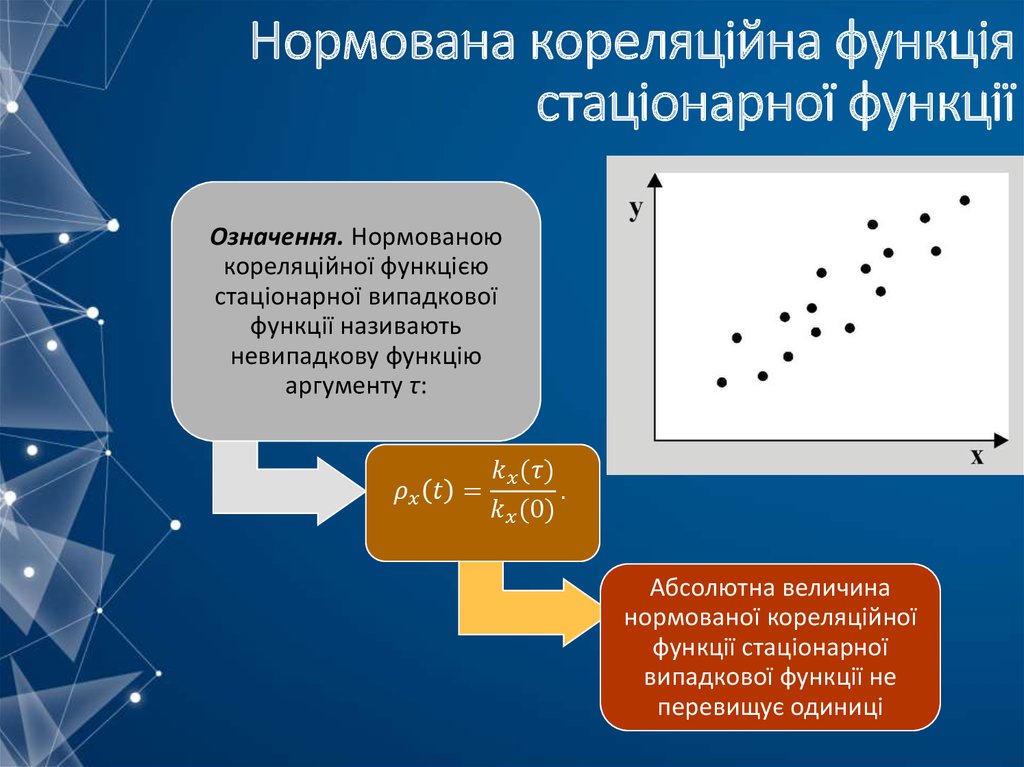



 mathematics
mathematics








