Применение генетических алгоритмов в информационных системах

1.

Санкт-Петербургский государственный университет
телекоммуникаций им. проф. М.А. Бонч-Бруевича
Применение генетических
алгоритмов в информационных
системах
Предмет : Введение в профессию
Подготовил : Храпунов Н. А.
Группа : ИСТ-114
Преподаватель : Литвинов В. Л.

2.

Цель и задачи исследования
Ознакомиться с понятием генетических алгоритмов
Проанализировать влияние биологических процессов на
понятие генетических алгоритмов
Изучить реализацию генетических алгоритмов в
информационных системах
Рассмотреть плюсы и минусы генетических алгоритмов, а
также их возможности применения

3.

План
Определение
Генетические алгоритмы и биология
Методы работы
Схема простого алгоритма
Ключевая функция
Пример работы
Отличия от других алгоритмов
Преимущества
Недостатки
Когда следует применять?
Вывод

4.

Определение
Генетический алгоритм (ГА) — это поисковая
оптимизация, основанная на принципах генетики и
естественного отбора.
Он часто используется для поиска оптимальных или
почти оптимальных решений сложных проблем, которые
в противном случае потребовались бы для решения
целой жизни.
Он также применим для решения задач оптимизации, в
исследованиях и в машинном обучении.

5.

Генетические алгоритмы и биология
Генетический
алгоритм
использует
механизмы, аналогичные естественному
отбору. Естественный отбор представляет
собой
процесс
выживания
и
преимущественного
размножения
приспособленных
представителей
популяции. Естественный отбор, по словам
Дарвина, точно так же постоянно фиксирует
любые изменения, сохраняет хорошие и
отбрасывает плохие, как это делает
селекционер, изучающий множество особей
и отбирающий и размножающий лучше из
них.

6.

Методы работы
Генетические
алгоритмы
для
решения
оптимизационных задач применяют методы
естественной эволюции, а именно:
• наследование,
• мутации,
• отбор,
• кроссинговер.

7.

Наследование - способность моделируемых объектов к мутации и
передаче решения проблемы следующему поколению, с целью
выработки развернутого решения.
Отбор объектов, которые будут унаследованы в каждом
последующем поколении, определяется фитнес-функцией, которая
зависит от решаемой проблемы.
Мутации – оператор, необходимый для «выбивания» популяции из
локального экстремума и препятствующий преждевременной
сходимости. Это достигается за счет того, что изменяется случайно
выбранный ген в хромосоме

8.

Для создания новой популяции можно использовать различные
методы отбора особей:
• Отбор усечением - использование популяции, состоящей как из
особей-родителей, так и особей-потомков, отсортированной по
возрастанию значений функции пригодности особей.
• Элитарный отбор - создание промежуточной популяции, которая
включает в себя как родителей, так и их потомков. Члены этой
популяции оцениваются, а за тем из них выбираются N самых
лучших (пригодных), которые и войдут в следующее поколение.
• Отбор вытеснением - выбор особи в новую популяцию зависит
не только от величины ее пригодности, но и от того, есть ли уже в
формируемой популяции особь с аналогичным хромосомным
набором

9.

Кроссинговер (скрещивание) – оператор, имеющий три типа:
• Одноточечный кроссинговер – при нём отцовские хромосомы
разделяются только в одной случайной точке
• Двухточечный кроссинговер хромосомы рассматриваются как
циклы, которые формируются соединением концов линейной
хромосомы вместе. Для замены сегмента одного цикла сегментом
другого цикла нужно выбрать две точки разреза.
• Многоточечный кроссинговер - Точки разрыва выбираются
случайно без повторений и сортируются в порядке возрастания.
При кроссинговере происходит обмен участками хромосом,
ограниченными точками разреза и таким образом получают двух
потомков. Участок особи с первым геном первой точке разреза в
обмене не участвует.

10.

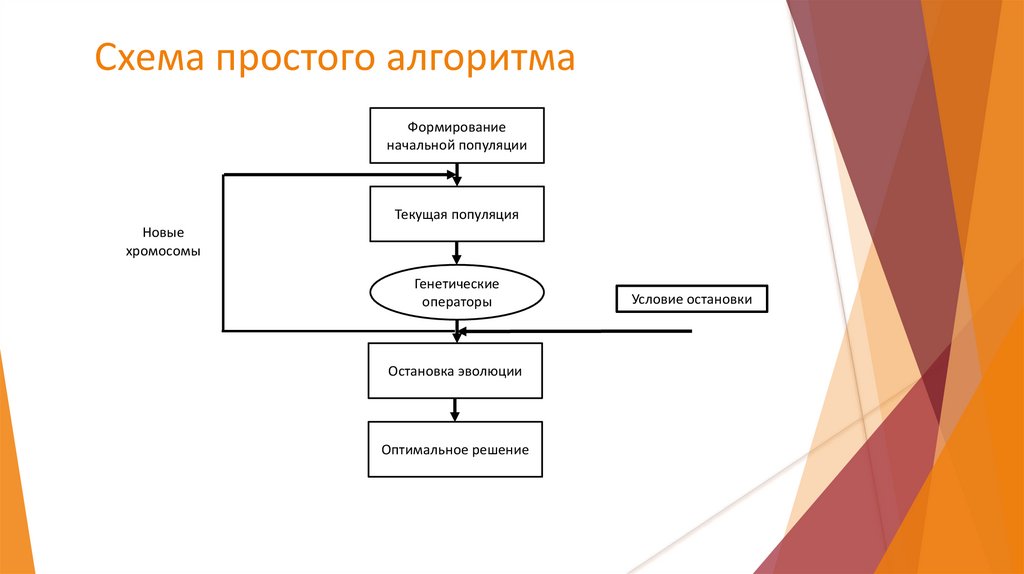
Схема простого алгоритма
Формирование
начальной популяции
Текущая популяция
Новые
хромосомы
Генетические
операторы
Остановка эволюции
Оптимальное решение
Условие остановки

11.

Ключевая функция
Входные данные: строка S
Выходные данные: натуральное число N, равное количеству
поколений необходимых для преобразования случайной
строки длины len(S) в строку S
Функция описана в коде ниже:

12.

Пример работы
Рассмотрим следующую строку: The quick brown fox jumps over the lazy dog и
воспроизведём вывод программы:
Как мы видим каждое поколение отличается не более, чем на один символ друг
от друга. Всего потребовалось 46 поколений, чтобы добраться
от rbbzmffwfhwtxnjjiozz ujhhlxeoyhezarquvmopyk до the quick brown fox jumps
over the lazy dog с помощью мутаций и отбора.

13.

Отличия от других алгоритмов
• Используются не параметры, а закодированная множества
параметров;
• Поиск осуществляется не из единственной точки, а из
популяции точек;
• В процессе поиска используются значения целевой функции,
а не её приращения;
• Применяются вероятные, а не детерминированные правила
поиска и генерации решений;
• Выполняется одновременный анализ различных областей
пространства решений, в связи с чем возможно нахождение
новых областей с лучшими значениями целевой функции за
счёт объединения квазиоптимальных решений из разных
популяций.

14.

Преимущества
• Способны находить глобальные оптимумы (с большей
вероятностью, чем традиционные алгоритмы);
• Можно применять в задачах, которые сложно формализовать
математически, либо даже совсем не имеющие математического
описания (функция приспособленности может быть выражена на
уровне алгоритма);
• Устойчивы к шуму (например, когда данные не могут быть точно
измерены или основаны на субъективном восприятии человека);
• Можно реализовать на уровне параллельных вычислений для
ускорения работы алгоритма;
• Возможность непрерывного обучения (оптимизации) популяции
при постоянном изменении окружающей среды (это изменение
сказывается на значениях функции принадлежности и популяции
необходимо постоянно подстраиваться под новые
обстоятельства).

15.

Недостатки
• Не гарантируется получение оптимального решения;
• эффективно сформулировать задачу, определить критерий отбора
хромосом (задать код) и другие параметры ГА может только специалист;
• Постановка задачи в терминах ГА не дает возможности проанализировать
статистическую значимость получаемого с их помощью решения;
• Достаточно высокая вычислительная ресурсоемкость ГА приводит к тому,
что в ходе моделирования эволюции многие решения отбрасываются как
неперспективные;
• При временной сложности в среднем ниже, чем у лучших конкурирующих
алгоритмов, но не более (получено на основе экспериментальных данных),
чем на один порядок;
• Невысокая эффективность на заключительных фазах моделирования
эволюции, объясняемая тем, что механизмы поиска ГА не являются жестко
ориентированными на скорейшее попадание в локальный оптимум;
• Не решенными остаются и некоторые другие вопросы, например
проблема самоадаптация ГА.

16.

Когда следует применять?
Генетические алгоритмы используются при
создании других вычислительных структур,
например, автоматов или сетей сортировки.
В машинном обучении они пригодны при
проектировании
нейронных
сетей
или
управлении роботами.
Они могут применяться при моделировании
развития в различных предметных областях,
включая биологические (экология, иммунология
и популяционная генетика), социальный (такие
как экономика и политические системы) и
когнитивные системы.

17.

Тем не менее, возможно наиболее популярное приложение
генетических алгоритмов - оптимизация многопараметрических
функций. Многие реальные задачи могут быть сформулированы
как поиск оптимального значения, где значение - сложная
функция, зависящая от некоторых входных параметров.
В некоторых случаях, представляет интерес найти те значения
параметров, при которых достигается наилучшее точное
значение функции.
В других случаях, точный оптимум не требуется - решением
может считаться любое значение, которое лучше некоторой
заданное величины. В этом случае, генетические алгоритмы часто наиболее приемлемый метод для поиска "хороших"
значений.

18.

Вывод
Сила генетического алгоритма заключена в его
способности манипулировать одновременно
многими
параметрами,
эта
особенность
алгоритма использовалась в сотнях прикладных
программ, включая проектирование самолетов,
настройку параметров алгоритмов и поиску
устойчивых состояний систем нелинейных
дифференциальных уравнений.

19.

Список источников
[coderlessons.com] Дата обращения 19.12.2021 URL : https://clck.ru/PqvvA
[pandia.ru] Дата обращения 19.12.2021 URL : https://clck.ru/ZQKLc
[4brain.ru] Дата обращения 19.12.2021 URL : https://clck.ru/JDJz9
[wikibgu.ru] Дата обращения 19.12.2021 URL : https://clck.ru/ZWuYr
[mathmod.asu.edu.ru] Дата обращения 19.12.2021 URL : https://clck.ru/ZWvvF
[info-farm.ru] Дата обращения 19.12.2021 URL : https://clck.ru/ZWxzF
[studopedia.su] Дата обращения 19.12.2021 URL : https://clck.ru/ZWzmv
[proproprogs.ru] Дата обращения 19.12.2021 URL : https://clck.ru/ZX2re
[knowledge.allbest.ru] Дата обращения 19.12.2021 URL : https://clck.ru/ZX2zN
[habr.com] Дата обращения 19.12.2021 URL : https://clck.ru/ZX6uu

20.

Спасибо за внимание!