Charles Darwin. The Origin of Species. John Murray, London, 1859.

Применение марковских цепей для моделирования поведения ГА

Задача поиска подмножества с требуемой суммой

3.13M

Category:

informatics

Оптимизационные методы искусственного интеллекта. Генетические алгоритмы

1.

Оптимизационные методы искусственного
интеллекта
Костенко Валерий Алексеевич
МГУ им. М.В. Ломоносова,
факультет ВМК
[email protected]
Сайт: https://asvk.cs.msu.ru
2024 г.

2. Генетические алгоритмы

3. План лекции

1. Простой генетический алгоритм Холланда.
2. Теория схем и гипотеза строительных блоков.
3. Генетический алгоритм с самообучением.

4. Charles Darwin. The Origin of Species. John Murray, London, 1859.

5. Генетический алгоритм Холланда (SGA)

• Holland J.N. Adaptation in Natural and
Artificial Systems. Ann Arbor, Michigan:
Univ. of Michigan Press, 1975.

6. Применение ГА

• построение оптимальных игровых
стратегий,
• машинное обучение (нейронные сети,
классификаторы),
• задачи математического
программирования,
• построение расписаний,
• задачи на графах (раскраска, задача
коммивояжера, нахождение
паросочетаний).

7. Генетический алгоритм Холланда (SGA)

• Основан на использовании механизмов
естественной эволюции:
1. Изменчивость
→ операция мутации
2. Наследственность
→ операция скрещивания
3. Естесственный отбор → операция селекции

8. Основные понятия

• Популяция - это множество битовых строк.
• Каждая строка - одно из возможных
решений задачи.
• По строке может быть вычислена функция
выживаемости, которая характеризует
качество решения.
• Основные операции алгоритма: селекция,
скрещивание и мутация выполняются над
элементами популяции.

9. Схема ГА

1. Сгенерировать случайным образом популяцию размера N.
2. Вычислить функцию выживаемости для каждой строки
популяции.
3. Выполнить операцию селекции.
4. Выполнить операцию скрещивания:
– 4.1. Выбрать пары для скрещивания.
– 4.2. Для каждой выбранной пары выполнить скрещивание,
получить двух потомков и произвести в популяции замену
родителей на их потомков.
5. Выполнить операцию мутации.
6. Если критерий останова не достигнут, перейти к п.2,
иначе завершить работу.

10. Требования к кодированию решений

1. Однозначность: каждая закодированная
строка должна соответствовать
единственному решению исходной задачи.
2. Возможность кодирования любого
допустимого решения.
3. Получение в результате генетических
операций корректных вариантов решений.
4. Возможность перехода от любого
корректного решения к любому другому
корректному решению.

11. Требования к кодированию решений

Для задач непрерывного и целочисленного
мат. программирования, оптимизируемые
параметры задаются:
– двоичным кодом числа,
– кодами Грея – двоичный код, последовательные
значения которого отличаются одним двоичным
разрядом.
0 - 0000
1 - 0001
2 - 0011
3 - 0010
4 - 0110
5 - 0111

12. Создание начальной популяции

• Случайным образом генерируется
начальная популяция в пределах
допустимых значений (в области поиска):

13. Вычисление функции выживаемости

• Выбирается согласно задаче
• Оценивает качество решения
• Применяется ко всем элементам популяции:

14. Операция селекции

• Схема пропорциональной селекции:
• Схема рулетки:
…

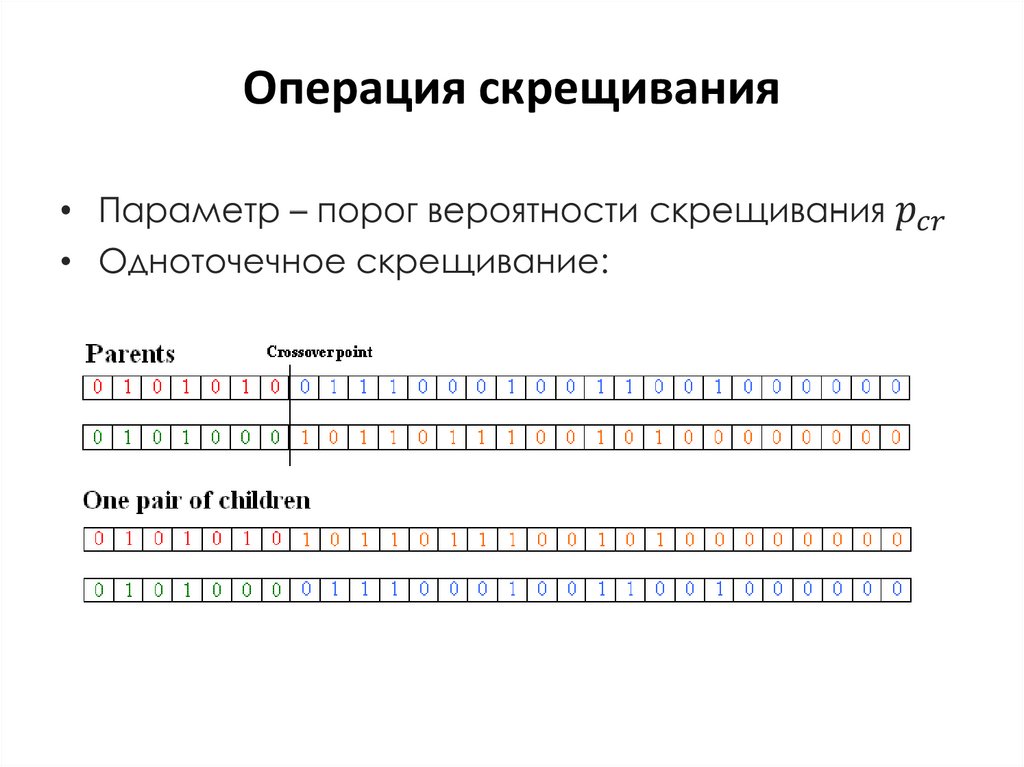
15. Операция скрещивания

16. Выбор пар для скрещивания

• Случайный выбор (требует популяций большого
размера).
• Селективный выбор – участвуют строки
значение функции выживаемости которых не
меньше среднего значения:
– имбридиг – первая строка выбирается случайно,
второй является максимально близкая к ней по
расстоянию.
– аудбридинг – формируются пары из максимально
далеких строк.
– комбинация этих подходов.

17. Операция мутации

18. Критерий останова

• Процесс продолжается итерационно
• Варианты критерия останова:
– Выполнение заданного числа итераций
– Выполнение заданного числа итераций без улучшения
– Достижение заданного значения функции выживаемости

19.

1. Простой генетический алгоритм Холланда.
2. Теория схем и гипотеза строительных блоков.
3. Генетический алгоритм с самообучением.
4. Задача построения расписания.
5. Задача поиска подмножества с требуемой суммой.

20. Cхемы

21. Cхемы

примеры схем

22. Cхемы

• Порядок схемы (K)- количество фиксированных
позиций в схеме:

23. Cхемы

• Определяющая длина схемы (L)– расстояние между
самыми дальними фиксированными позициями:

24. Cхемы

25. Cхемы

• Для любой схемы, представляющей
хорошее решение, нужно, чтобы
количество ее примеров увеличивалось с
увеличением количества итераций
• На преобразование схем влияют
операции ГА: мутация, скрещивание и
селекция

26. Теорема схем

27. Теорема схем

28. Теорема схем

29. Теорема схем

30. Теорема схем

31.

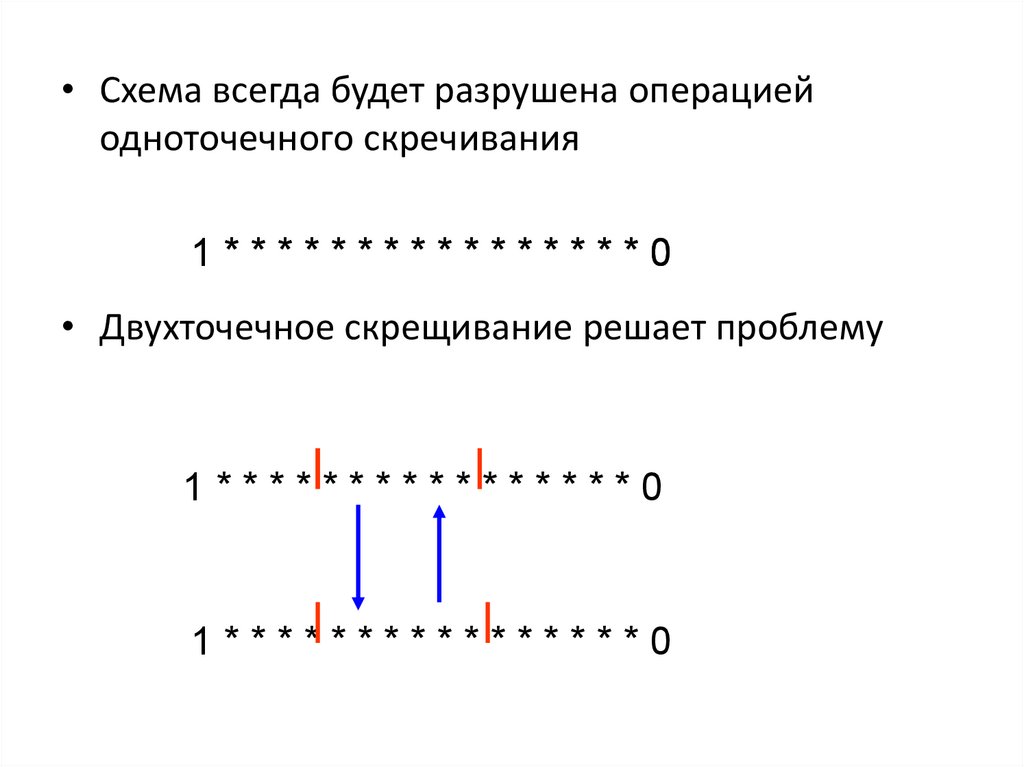
• Схема всегда будет разрушена операцией
одноточечного скречивания
1****************0
• Двухточечное скрещивание решает проблему
1****************0
1****************0

32. Теорема схем

• Проблема выбора параметров ГА является для
многих приложений сложной задачей
• Теоретические результаты для решения данной
проблемы на данный момент отсутствуют
• На практике данная проблема решается
экспериментальным путем

33. Гипотеза строительных блоков

• Строительные блоки - схемы с низким порядком,
малыми определяющими длинами и большими
значениями средних целевых функций
• Гипотеза строительных блоков: комбинирование
хороших строительных блоков дает хорошую
строку.

34. Применение марковских цепей для моделирования поведения ГА

• Марковская цепь – вероятность того, что процесс в
момент времени t будет в состоянии j, зависит только
от состояния i в момент (t-1).
• Состояние ГА – текущая популяция.
• Множество всех состояний – множество
всевозможных популяций.
• Построить модель – определить вероятность
перехода между популяциями (построить матрицу
переходов).
При n=8 и N=8 матрица переходов имеет более
10 ^29 элементов.

35. 36. ГА с самообучением

• Идея:
– ввести индивидуальные параметры
вероятности операций мутации и скрещивания
для каждого элемента строки-решения
– корректировать эти параметры на каждой
итерации алгоритма в зависимости от того,
насколько удачным или неудачным оказалось
применение конкретной операции к элементу
решения

37. ГА с самообучением

• Костенко В. А., Фролов А. В. Генетический
алгоритм с самообучением // Известия РАН.
Теория и системы управления, 2015, № 4, С. 24-38.
DOI: 10.7868/S0002338815040101.
• V.A. Kostenko, A.V. Frolov. Self-Learning Genetic
Algorithm // Journal of Computer and Systems
Sciences International, 2015, Vol. 54, No. 4, pp.
525–539. DOI: 10.1134/S1064230715040103

38. Матрицы вероятности

39. Схема ГА c самообучением

40. Операция скрещивания

41. Операция мутации

42. Способы коррекции элементов МП

43. Способы коррекции элементов МП

44. Способы коррекции элементов МП

45. 46. Задача построения расписания

47. Модель прикладной программы

• Ацикличный ориентированный граф
• ik pi , pk i ,k 1 K - дуги

48. Модель прикладной программы

• Задается:
1.
Множеством работ:
2.
Отношением
3.
Вычислительными сложностями работ:
:
ik pi , pk i ,k 1 K

49. Модель расписания

• HP
M
i
i 1
c

50. Математическая постановка

51. Кодирование решений

- привязка
- приоритеты

52. Матрицы вероятности

53. Функция выживаемости

• Ограничена сверху:

54. Операции генетического алгоритма

• Cелекция: смешанная стратегия
• Скрещивание: одноточечное
• Мутация: стандартная

55. Критерий останова

o Ограничение на число итераций алгоритма, т.е. алгоритм прекращает
свою работу, если не смог за I0 шагов улучшить значение функции
выживаемости в популяции.

56. .

57. Задача поиска подмножества с требуемой суммой

58. Кодирование решений

59. Матрицы вероятности

60. Функция выживаемости

61. Операции генетического алгоритма

• Cелекция: смешанная стратегия
• Скрещивание: равномерное с замещением
• Мутация: стандартная

62. Критерий останова

• Итерационный процесс до достижения
критерия останова
• Совокупность условий:
– Выполнение заданного числа итераций без улучшения (без
уменьшения наименьшего значения функции выживаемости)
– Достижение функцией выживаемости значения 0

English Русский Rules