Групповой выбор

1.

ГРУППОВОЙ ВЫБОР
Под групповым выбором понимаются преобразования различных индивидуальных мнений о
рассматриваемых объектах в единое "коллективное " мнение .
Это позволяет трактовать проблему группового выбора как общую проблему перехода от заданных
"индивидуальных наборов данных" к единому "групповому набору данных".
эксперты и их оценки(анализ экспертных оценок),
избиратели и их "голоса"(модели голосования),
показатели качества и их значения(многокритериальные решения),
качественные признаки и порождаемые ими разбиения (классификации
финансирование общественных благ
трагедия общины (истощение ресурсов из-за чрезмерного использования)
дилемма заключенного (доминирующие стратегии ведут к худшему исходу)
асимметричность информации (отрицательный отбор; моральный риск).
объектов),

2.

Основные принципы группового выбора
1 Принципы согласования - правило большинства
• Принцип большинства голосов
• Принцип вето
• Принцип диктатора
В группе ЛПР могут образовываться коалиции — объединения участников в подгруппы с
совпадающими целями. Этот принцип утверждает, что групповое предпочтение должно соответствовать
коалиции, которая имеет число членов, иначе голосов, превышающее некий порог. Этот порог может быть
равен половине участников группового ЛПР. В этом случае говорят о принципе простого большинства. Если
порог равен 2/3 голосов, то говорят о принципе большинства в 2/3 голосов, и если порог равен числу всех
участников, то говорят о единогласном решении, или принципе абсолютного большинства.

3.

Принцип вето. Этот принцип согласования решения требует формального согласия всех участников решения и
состоит в том, что если хотя бы один из участников решения не согласен с предлагаемым вариантом (т. е.
накладывается «вето»), значит, решение не принимается.
Принцип вето, таким образом, требует единогласия для реализации решения. Этот принцип целесообразно применять
для важных, ответственных решений со значительными последствиями. Например, принцип вето в Совете
безопасности ООН, число участников которого ограничено 7–8 членами — ведущими странами мира означает, что
каждый из участников может предложить свой вариант решения, но осуществление решения, включающее
финансирование за счет средств ООН, возможно только при одобрении или не возражении всех остальных участников
Совета безопасности.
Принцип диктатора. Этот принцип применяется в военных организациях и при принятии решений в
чрезвычайных обстоятельствах. Согласно этому принципу в качестве группового предпочтения принимается
предпочтение одного лица группы — диктатора.
При решениях по этому принципу не учитываются предпочтения других участников решения, по существу
групповое предпочтение в данном случае соответствует индивидуальному предпочтению.
Как принцип диктатора, так и принцип большинства голосов не учитывают интересы всех членов группы.
Применение этих принципов не обеспечивает устойчивости существования группы участников решения и при
отсутствии других сдерживающих факторов может привести к распаду группового ЛПР.

4.

2 Принцип обеспечивающий учет интересов всех членов группы
Принцип КУРНО выражает индивидуалистическую рациональность в котором
оптимальным считается такое состояние, в котором один из показателей имеет наилучшее
значение. (Этот принцип отражает индивидуальную рациональность: никому из членов группового ЛПР отдельно
невыгодно менять решение, поскольку не существует лучшего. Принцип действует только тогда, когда индивидуальные
предпочтения для вариантов решения таковы, что каждому участнику они не приносят большого ущерба или выгоды.)
Принцип ПАРЕТО выражает коллективистскую рациональность, где оптимальным
считается такое состояние в котором улучшение одних показателей приводит к ухудшению
других показателей, т .е.. ущемление интересов даже одного индивидуума недопустимо. (Всем
членам группы сразу невыгодно менять оптимальное решение, поскольку не существует лучшего решения. По
принципу Парето группа может улучшать свои решения без нанесения ущерба каждому члену, поэтому его применение
возможно только при сильной зависимости всех членов группового ЛПР.)

5.

Принцип ЭДЖВОРТА наиболее полно выражает коллективистскую
рациональность, где каждое подмножество показателей состояния имеет
наилучшие значения, т.е. никакой коалиции не выгодно менять состояние
равновесия. (Если число участников решения в каждой коалиции больше одного, то их
предпочтения могут быть таковы, что каждой из коалиций не выгодно менять свое решение, когда у
них нет лучшего решения.)

6.

Выбор принципа согласования должен осуществляться на основе характера отношений между
коалициями (членами).
Основными типами отношений между коалициями принимаются отношения:
1 статус-кво
При отношении статус-кво коалиции стараются сохранить существующее положение. Это отношение
определяется взаимодействиями слабосвязанных участников и характерно для экономических структур и
организаций.
Сильные взаимодействия, к ним относятся конфликты, определяют отношения конфронтации и
рациональности.
2 конфронтации или соперничества
При отношении конфронтации коалиции действуют так, чтобы принести ущерб друг другу.
3 рациональности
Стратегия рациональности характерна для субъектов конфликта, когда они оценили со всех сторон свое
положение и ресурсы, которыми они еще располагают, а также возможности противника, баланс сил, и
приняли решение о дальнейшем взаимодействии. При отношениях рациональности коалиции действуют в
собственных интересах для получения максимального результата, что не обязательно приносит ущерб
другим коалициям.
Разрешение конфликта — это всегда некоторое коллективное (групповое) решение при несовпадающих целях. И поэтому любое
коллективное решение это всегда компромисс. Главное — добиться успеха минимальной ценой. Каждый из партнеров,
участвующих в конфликте, преследует свои цели.

7.

8.

9.

10.

11.

12.

13.

14.

15.

ПРИМЕР Парадокс Кондорсе
Рассмотрим пример голосования в собрании представителей из 60 чел. Пусть на голосование поставлены
три кандидата: А, В и С, и голоса распределились, как в табл. 1.1.
Сравним предпочтения в парах кандидатов. Берем А и С: тогда А предпочитают 23+2=25; С по сравнению
с А предпочитают: 17+10+8=35. Следовательно, С предпочтительнее А (С -> А) по воле большинства.
Таблица 1.1 Распределение голосов (парадокс Кондорсе)
Число голосующих
23
17
2
10
8
Предпочтения
A->B->C
B->C->A
B->A->C
C->A->B
C->B->A
Сравнивая попарно аналогичным образом А и В, В и С, получаем: В -> С (42 против 18), С -> А (35
против 25) и А -> В (33 против 27). Возникло противоречие, А -> В -> С -> А.
Столкнувшись с этим парадоксом, Кондорсе выбрал наименьшее зло, а именно то мнение, которое
поддерживается большинством голосов (избранным следует считать А).

16.

Вывод. Даже если индивидуальный выбор относительно каких-либо альтернатив голосования (три
альтернативы и более) рационален, коллективный выбор может не обладать свойством транзитивности,
т. е. из выполнения условий A > B и B > C не будет следовать A > C. В этом случае исход голосования будет
определяться использованием той или иной процедуры голосования. Тогда, организуя определенным
образом эту процедуру, можно управлять выбором победителя.
В подобных ситуациях большое значение приобретает «составитель повестки дня» — тот, кто
решает, какие альтернативы должны ставиться на голосование и может подобрать варианты
так, чтобы получить результат, соответствующий его собственным предпочтениям

17.

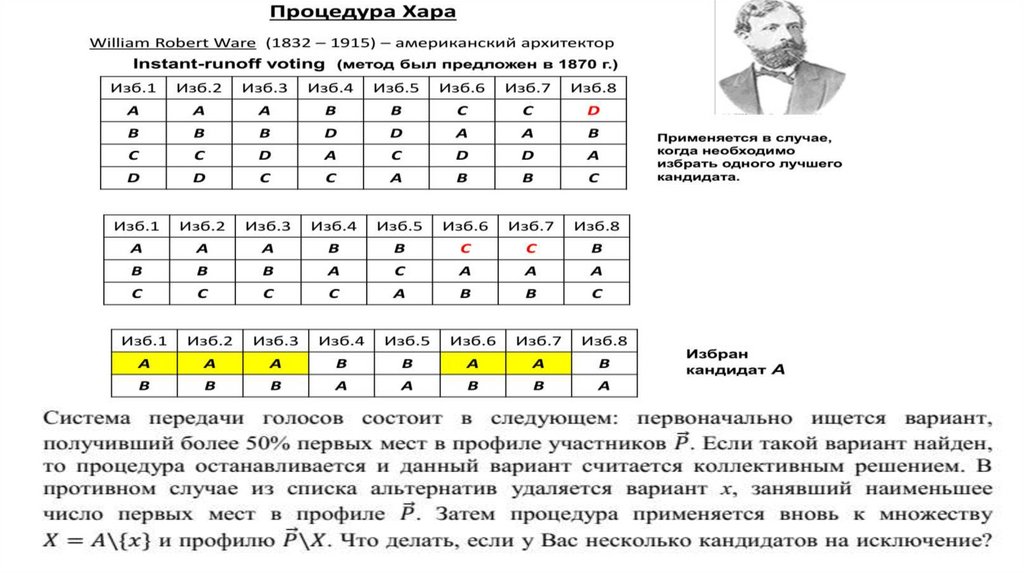
Второй тур.
Рассмотрим широко применяющуюся практику голосования в два этапа, когда во
второй тур выборов выходят два кандидата, за которых проголосовало наибольшее
число избирателей.
Число
голосующих
Предпочте
ния
Число
голосующих
Предпочтен
ия
23
A->B->C
23
A->B->C
17
B->C->A
17
B->C->A
2
B->A->C
2
А->B->C
10
C->A->B
10
C->A->B
8
C->B->A
8
C->B->A
В соответствии с предпочтениями, во второй тур выходят А (23 голоса) и В
(17+2=19 голосов), после чего побеждает А. Допустим теперь, что первоначальные
позиции А немного усилились (табл. справа), и предпочтения двух избирателей (в 3ей строке) выглядят теперь как А -> В -> С.
Тогда во второй тур выходят А (25
голосов) и С (18 голосов), после чего побеждает С!!!

18.

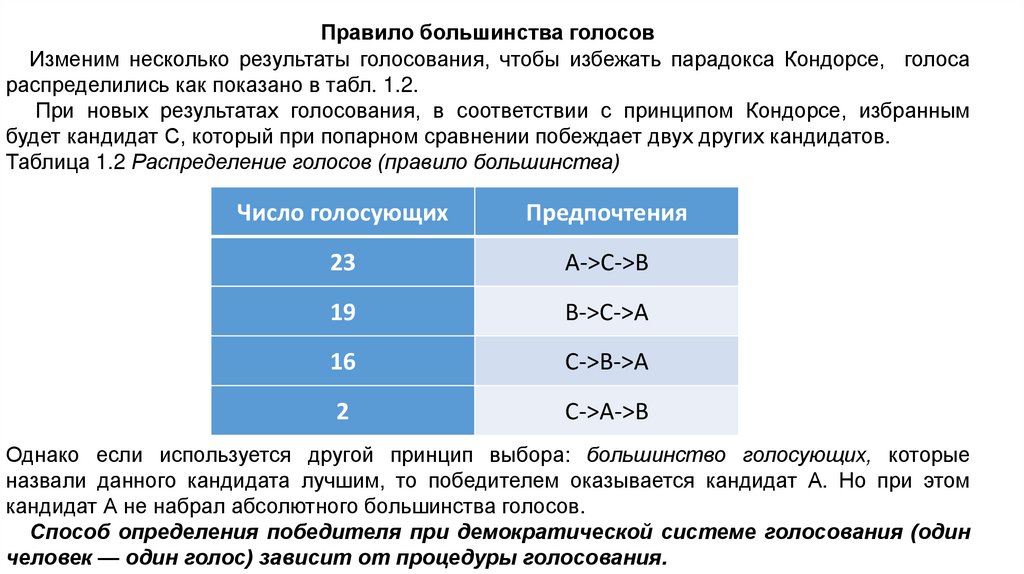
Правило большинства голосов
Изменим несколько результаты голосования, чтобы избежать парадокса Кондорсе, голоса
распределились как показано в табл. 1.2.
При новых результатах голосования, в соответствии с принципом Кондорсе, избранным
будет кандидат С, который при попарном сравнении побеждает двух других кандидатов.
Таблица 1.2 Распределение голосов (правило большинства)
Число голосующих
Предпочтения
23
A->C->B
19
B->C->A
16
C->B->A
2
C->A->B
Однако если используется другой принцип выбора: большинство голосующих, которые
назвали данного кандидата лучшим, то победителем оказывается кандидат А. Но при этом
кандидат А не набрал абсолютного большинства голосов.
Способ определения победителя при демократической системе голосования (один
человек — один голос) зависит от процедуры голосования.

19.

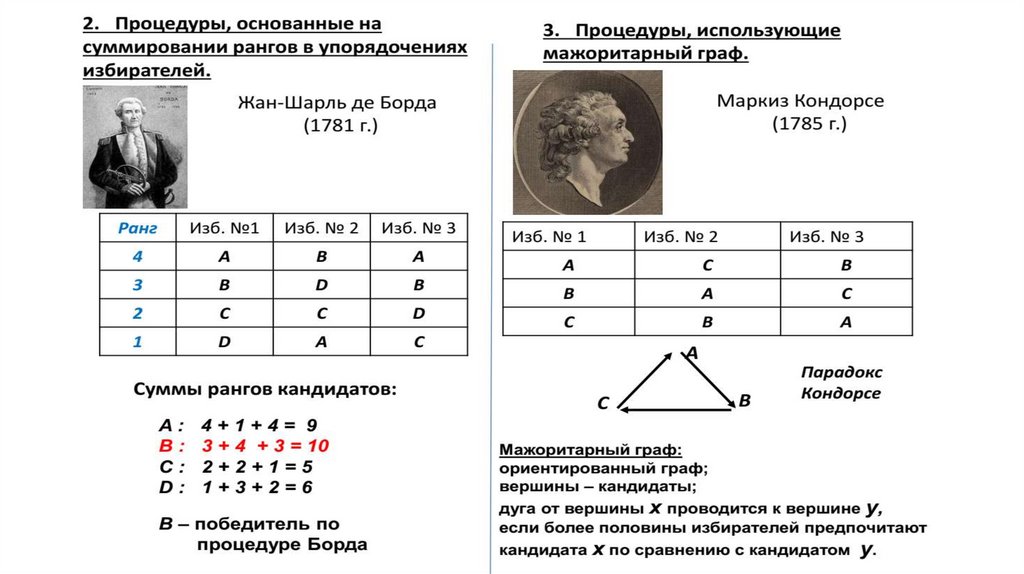
Метод Борда
Согласно этому методу результаты голосования выражаются в виде числа баллов,
набранных каждым из кандидатов. Пусть число кандидатов равно п. Тогда за первое
место присуждается п баллов, за второе — ( n —1), за последнее — один балл.
Применим метод Борда к приведенному выше примеру (см. табл. 1.2). Подсчитаем
число баллов для каждого из кандидатов:
A:23x3 + 19xl + 16xl + 2x2 = 108;
B:23xl + 19x3 + 16x2 + 2xl = 114;
С:23х2 + 19х2 + 16х3 + 2хЗ = 138.
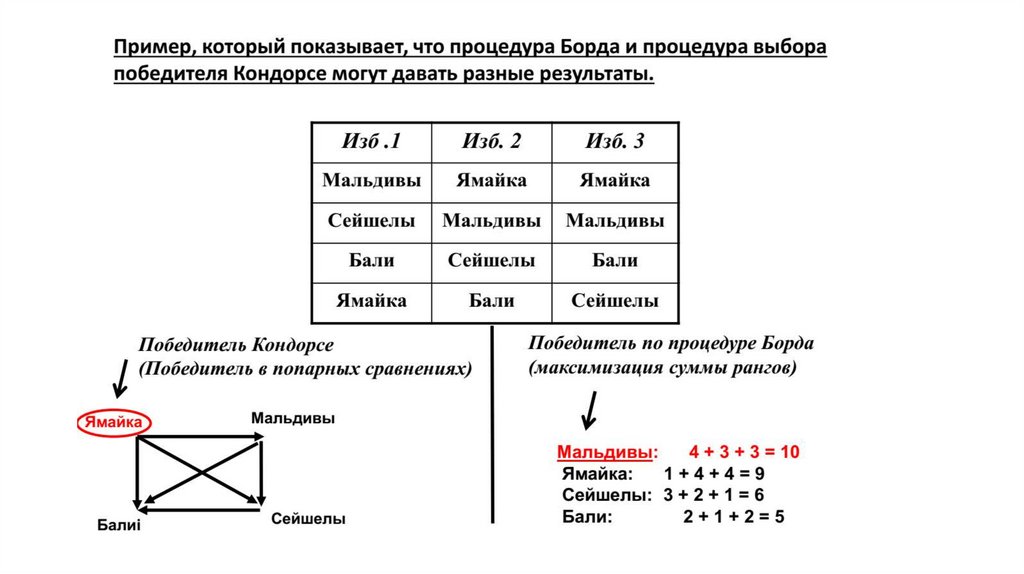
В соответствии с методом Борда мы должны объявить победителем кандидата С
который проигрывает по большинству голосующих.
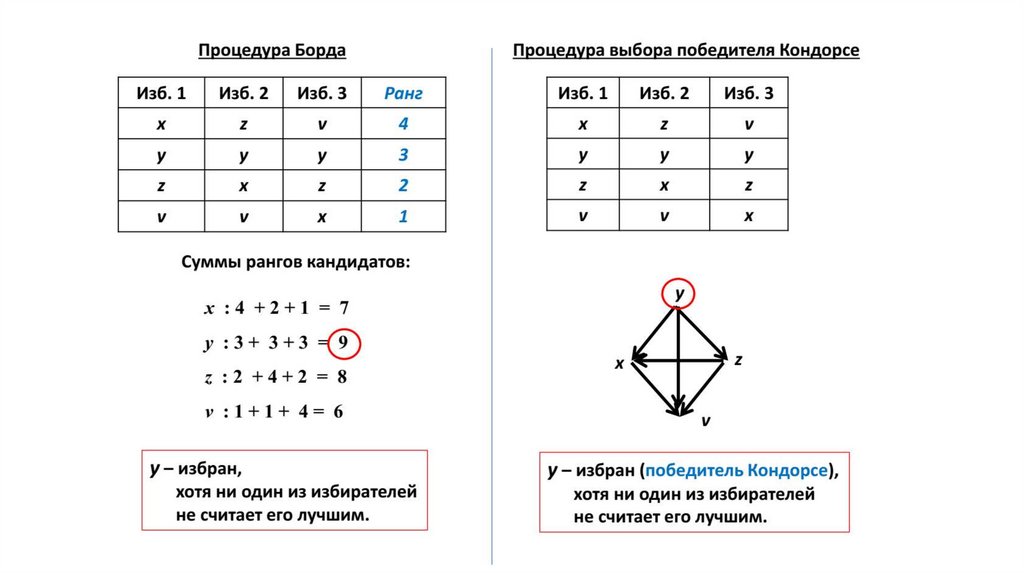
Однако с методом Борда, как и с принципом Кондорсе, возникают проблемы.

20.

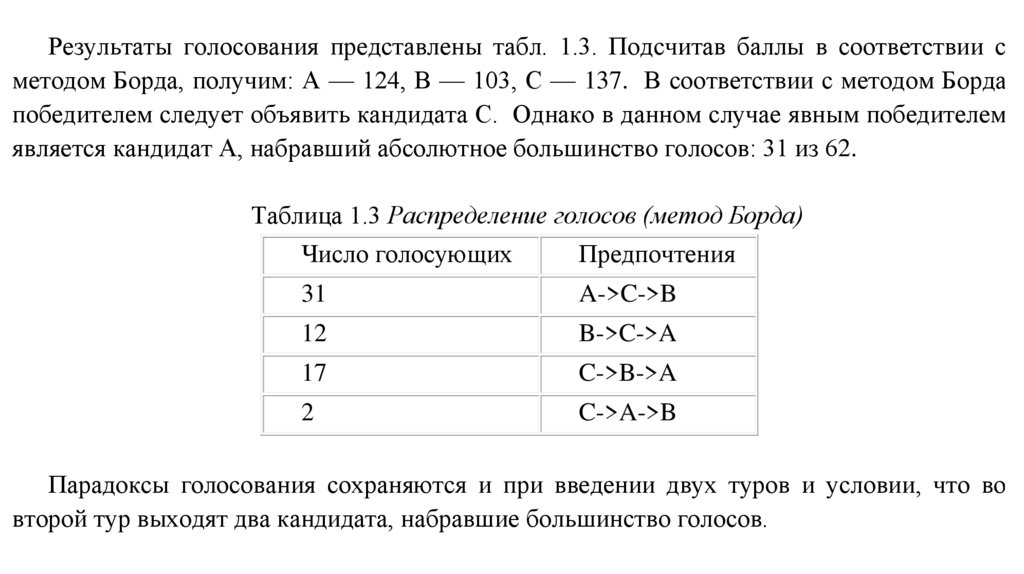
Результаты голосования представлены табл. 1.3. Подсчитав баллы в соответствии с
методом Борда, получим: А — 124, В — 103, С — 137. В соответствии с методом Борда
победителем следует объявить кандидата С. Однако в данном случае явным победителем
является кандидат А, набравший абсолютное большинство голосов: 31 из 62.
Таблица 1.3 Распределение голосов (метод Борда)
Число голосующих
Предпочтения
31
A->C->B
12
B->C->A
17
C->B->A
2
C->A->B
Парадоксы голосования сохраняются и при введении двух туров и условии, что во
второй тур выходят два кандидата, набравшие большинство голосов.

21.

Задание 1
Какой кандидат выиграет А,Б,С по методу Кондорсе и по методу Борда для
заданного распределения голосов?
Число голосующих
Предпочтение
34+№вар
А Б С
23+№вар
А С Б
26 - №вар
С Б А
2+№вар
Б С А
13+№вар
С А Б