Сложение и умножение вероятностей

1.

Цели обучения
10.3.2.3 понимать и применять правила сложения
вероятностей
* P(A + B) = P(A) + P(B)
* P(A +B) = P(A) + P(B) – P(A ∙ B);
10.3.2.4 понимать и применять правила
умножения вероятностей
* P(A ∙ B) = P(A) ∙ P(B)
* P(A ∙ B) = P(A) ∙ PA(B) = P(B) ∙ PB(A);

2.

Цель урока
• знает и понимает теоремы сложения и
умножения вероятностей;
• применяет теоремы сложения и умножения
вероятностей при решении задач.

3.

1 урок

4.

Математический ребус
вероятность

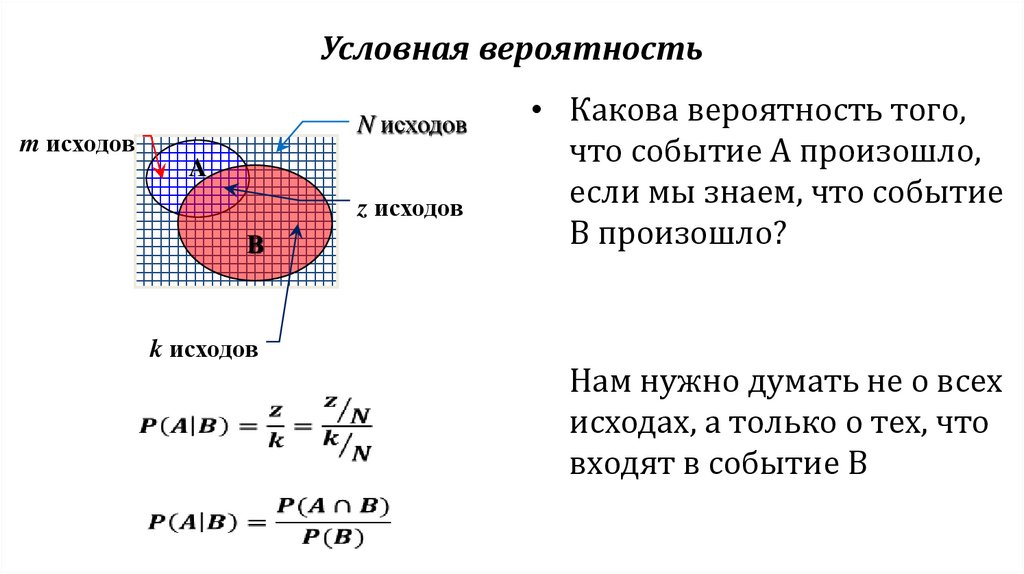
5. Условная вероятность

УСЛОВНАЯ ВЕРОЯТНОСТЬ
Условной вероятностью называется
вероятность события A, вычисленная в
предположении, что событие B уже
наступило.

6. Условная вероятность

N исходов
m исходов
A
z исходов
B
k исходов
• Какова вероятность того,
что событие A произошло,
если мы знаем, что событие
B произошло?
Нам нужно думать не о всех
исходах, а только о тех, что
входят в событие B

7.

Пример 1
Из ящика, содержащего 4 белых и 7 чёрных шаров наудачу последовательно
извлекаются 2 шара. Найти вероятность того, что 2-й шар - чёрный при
условии, если первым был извлечён белый шар.

8.

Два события называют
НЕСОВМЕСТНЫМИ,
если в одном и том же испытании они не могут
произойти одновременно, то есть
наступление одного из них исключает наступление
другого.

9. теорема сложения вероятностей несовместных событий

ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ
НЕСОВМЕСТНЫХ СОБЫТИЙ
Вероятность появления одного из двух
несовместных событий, безразлично
какого, равна сумме вероятностей этих
событий.

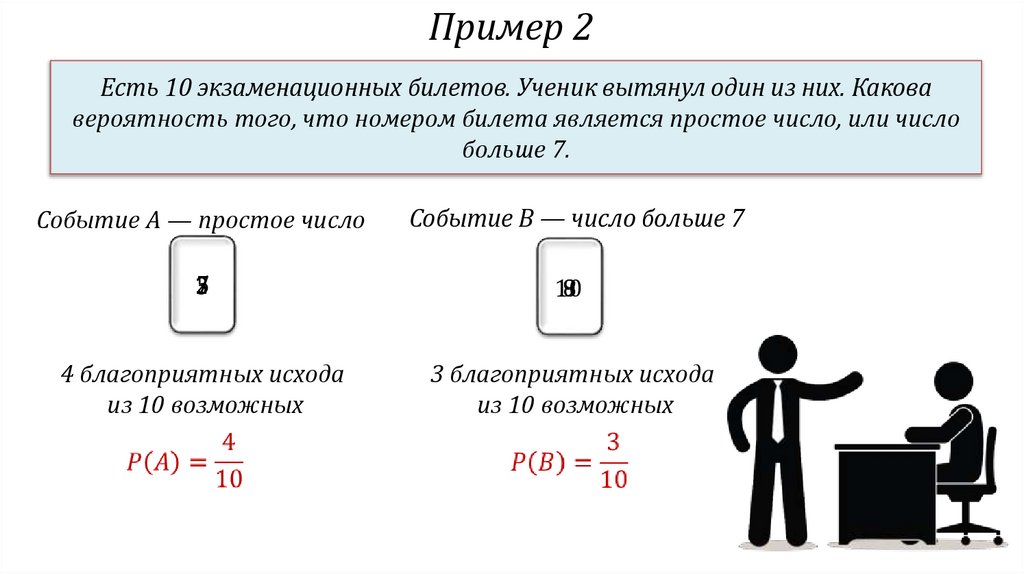
10.

Пример 2
Есть 10 экзаменационных билетов. Ученик вытянул один из них. Какова
вероятность того, что номером билета является простое число, или число
больше 7.
Событие А — простое число
Событие B — число больше 7
5
7
2
3
9
8
10
4 благоприятных исхода
из 10 возможных
3 благоприятных исхода
из 10 возможных

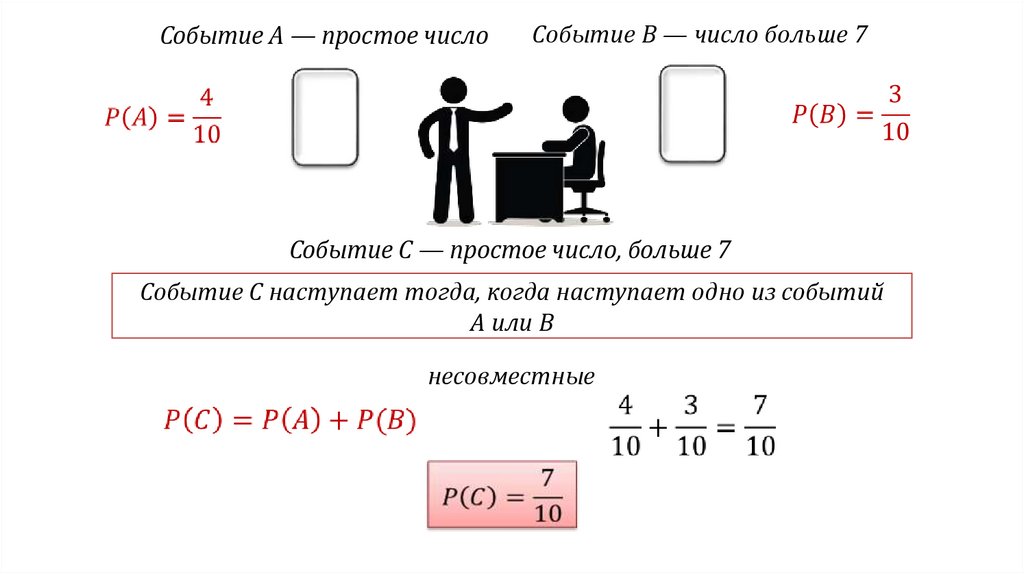
11.

Событие А — простое число
Событие B — число больше 7
Событие C — простое число, больше 7
Событие С наступает тогда, когда наступает одно из событий
A или B
несовместные

12.

Два события называются
совместными,
если появление одного из них не исключает
появление другого
в одном и том же испытании.

13. теорема сложения вероятностей совместных событий

ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ
СОВМЕСТНЫХ СОБЫТИЙ
Вероятность появления хотя бы одного
из двух совместных событий равна сумме
вероятностей этих событий без
вероятности их совместного появления

14.

Пример 3
Есть 10 экзаменационных билетов. Ученик вытянул один из них. Какова
вероятность того, что номером билета является число,
которое делится на 2 или на 3.
Событие А — делится на 2
Событие B — делится на 3
5 благоприятных исхода
из 10 возможных
3 благоприятных исхода
из 10 возможных
Событие АB — делится на 2 и на 3
1 благоприятный исход
из 10 возможных

15.

Пример 3
Есть 10 экзаменационных билетов. Ученик вытянул один из них. Какова
вероятность того, что номером билета является число,
которое делится на 2 или на 3.

16. Решение задач

Приложение 1

17.

Подведем итоги
- что узнал, чему научился?
- что осталось непонятным?
- над чем необходимо работать?