Доменна структура та процеси намагнічування. Енергія обмінної взаємодії.Лекція 6

1.

Доменна структура та процеси намагнічування.
Енергія обмінної взаємодії
Для магнітовпорядкованих феромагнітних кристалів характерно те, що магнітні моменти атомів спрямовані
паралельно один одному всередині хоча і невеликих, але макроскопічних областей, що називаються доменами. При
цьому спіни прагнуть орієнтуватися паралельно один одному завдяки наявності особливої форми кулонівської
взаємодії - обмінній взаємодії. Порушення паралельності спінів викликається тепловим рухом електронів. Крім того,
існують доменні границі - шари з непаралельними спінами, що розділяють домени з різною орієнтацією
намагніченості. За рахунок цього порушення паралельності виникає добавка до величини обмінної взаємодії.
Виявляється, при утворенні доменної структури і в процесах технічного намагнічування визначальну роль грає саме
ця добавка до величини обмінної енергії за рахунок непаралельності спінів, оскільки вона порівнянна по порядку
величини з зеєманівською енергією магнетика в зовнішньому полі намагнічування.
Обчислення величини обмінної енергії в загальному випадку є надзвичайно складним завданням. Обмежимося лише
розглядом найпростішого випадку - парної обмінної взаємодії, тобто припустимо, що найбільший внесок в обмінну
енергію вносить взаємодія найближчих сусідів і що іншими видами взаємодій можна знехтувати.
Енергію обмінної взаємодії для двох спінів можна записати у вигляді
В цьому виразі добуток двох спінових операторів замінено на
скалярний добуток двох векторів Si та Sj. однакових за величиною
та кутом ij між ними.
Кут ij для феромагнетика близький до нуля, тому можна вважати
Отже, добавка до обмінної енергії за рахунок непаралельності спінів буде мати вигляд.
А повна добавка
При вивченні макроскопічних властивостей зручніше перейти до суцільного середовища, тоді для косинусів
зручніше використовувати інші вирази

2.

Енергія обмінної взаємодії.
Нехай ui та uj одиничні вектори в напрямку спінів Si та Sj. Тоді:
Де 1, 2 та 3 з відповідними індексами – направляючі косинуси вектора спіну. Оскільки ми будемо
розглядати невеликі відхилення спінів від деякого напрямку, то вектор uj можна розкласти в ряд околі
вектора ui. Тоді, складові li lj в попередньому виразі можна подати у вигляді:
При виконанні сумування в енергії обмінної взаємодії по найближчим сусідам складові типу
для кубічних кристалів рівні нулеві внаслідок симетрії
Тоді сума по найближчим сусідам буде мати вигляд:
Оскільки
то
Друга складова і визначає додатковий внесок в обмінну енергію

3.

Енергія обмінної взаємодії
Можна показати, що питоме значення енергії обмінної взаємодії може бути виражено у вигляді:
Де А залежить від типу кристалічної структури
Примітивна, кубічна
ОЦК
ГЦК
Магнітна кристалографічна анізотропія.
Якщо у феромагнетику враховувати тільки ізотропну обмінну взаємодію, то цілком зрозуміло, що енергія такої
взаємодії не буде залежати від напрямку вектору намагнічування вздовж окремих кристалографічних осей. В той
же час, проведені експериментальні дослідження показують, що навіть для кубічних кристалів така залежність
існує, тобто, намагніченість феромагнітного кристалу старається орієнтуватися вздовж деяких кристалографічних
напрямків, що називаються напрямками легкого намагнічування. Досить часто ці напрямки мають вигляд площини
легкого намагнічування. При намагнічуванні кристалу в інших напрямках приходиться прикладати значні поля.
Причина такої анізотропії – наявність спін-орбітальної взаємодії та магніто-дипольна взаємодія, які суттєво
залежать від типу структури.
Феноменологічний вираз для енергії магнітної кристалографічної анізотропії можна отримати виходячи з
міркувань симетрії. Для прикладу, для одноосних кристалів ця енергія буде мати вигляд:
Тут, кут між вектором намагнічування та виділеною віссю,
Кn – не залежні від кута константи магнітної анізотропії

4.

Магнітна кристалографічна анізотропія.
В більшості випадків достатньо обмежитися лише декількома членами ряду:
При К1<0 та К2=0 матиме місце вісь легкого намагнічування, оскільки мінімум енергії буде відповідати
куту між виділеною віссю та вектором намагнічування =0, тобто намагнічування відбувається при
прикладанні магнітного поля вздовж цієї кристалографічної осі.
При К1>0 К2=0 матимемо площину легкого намагнічування
Можливі і більш складні випадки напрямків легкого намагнічування.
Для кубічних кристалів слід врахувати еквівалентність чотирьох направляючих косинусів і відносно
кристалографічних осей. Врахування виразу: 12+ 22+ 32=1 та ряду інших співвідношень дозволяє записати вираз
для кубічних кристалів у вигляді:
Залежно від коефіцієнтів Кі можливі різні випадки розміщення напрямків легкого та важкого намагнічування.
Приклади кривих намагнічування вздовж різних
напрямків для різних кристалів
Fe
Ni
Константи залежні від температури
Co

5.

Наведена або орієнтаційна магнітна анізотропія.
Магнітну анізотропію можна створити штучним шляхом за допомогою особливої технологічної обробки
матеріалу. Наприклад, холодною прокаткою, відпалом в магнітному полі, перекристалізацією в магнітному полі,
нанесенням плівок в магнітному полі і т.д.
Важлива роль у цьому випадку відводиться різним дефектам. В процесі відпалів, цілком зрозуміло нижче
температури Кюрі, дефекти за рахунок дифузійних процесів намагаються розмітитися таким чином, щоб
стабілізувати наведений магнітними полями розподіл векторів намагнічування. При охолодженні структура
дефектів залишається незмінною, тому і буде існувати певний напрям, вздовж якого і буде енергетично вигідно
розміщуватися векторам намагнічування. Тобто, виникає вісь легкого намагнічування.
Об'ємна або однонаправлена магнітна анізотропія.
Дана магнітна анізотропія виникає на межі розділу феромагнітної та антиферомагнітної фази. Вона була виявлена на
дисперсних частинках кобальту (феромагнетик), що покритих оксидом СоО (антиферомагнетик). Еефктивно вона
проявляється на частинках малих розмірів. Її прояв можна описати виразом:
Тобто існує напрям, а не вісь легкого намагнічування.
Виникає вона за рахунок обмінних взаємодій між поверхневими електронами феромагнетика та спінами
антиферомагнетика. За рахунок такої взаємодії утворюється свій специфічний розподіл векторів намагнічування.
При перемагнічуванні феромагнетика, напрям спінів у антиферомагнетику не змінюється, оскільки його
перемагнічування відбувається в досить великих полях. Тому обмінна взаємодія з поверхневими атомами утруднює
зміну напрямку поверхневих спінів феромагнетику. Для зміни їх напрямків потрібно виконати роботу проти
обмінних сил.
Типовий прояв такої анізотропії
Зміщення кривої намагнічування .

6.

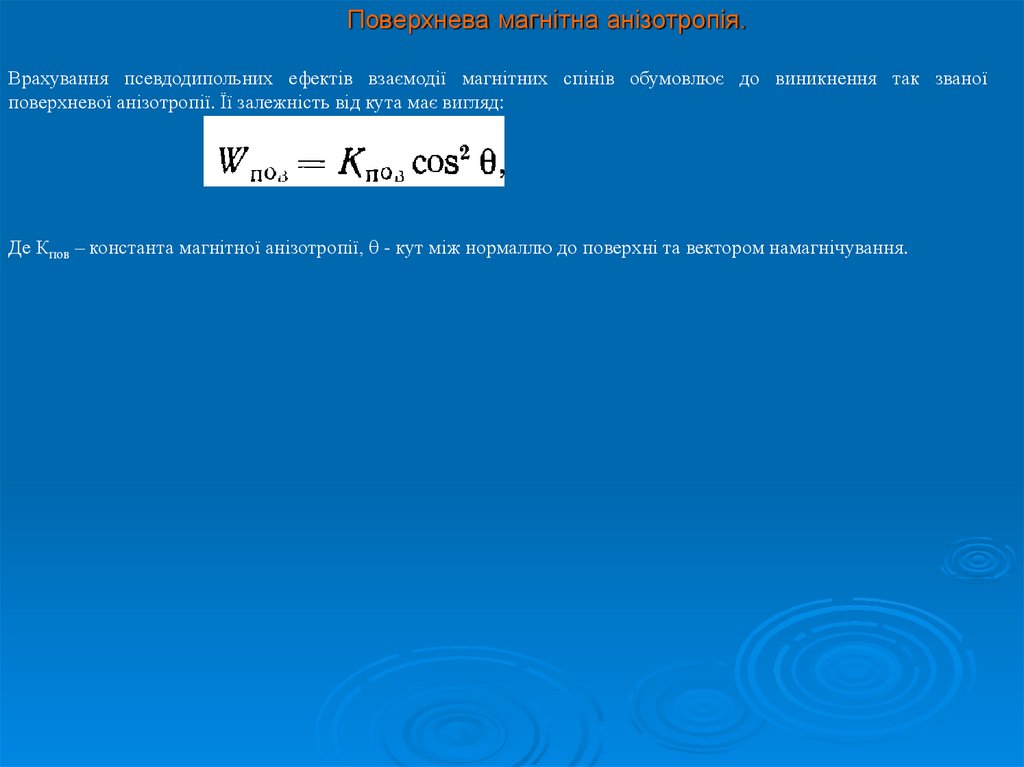
Поверхнева магнітна анізотропія.
Врахування псевдодипольних ефектів взаємодії магнітних спінів обумовлює до виникнення так званої
поверхневої анізотропії. Її залежність від кута має вигляд:
Де Кпов – константа магнітної анізотропії, - кут між нормаллю до поверхні та вектором намагнічування.