Множества и логика в задачах ЕГЭ по информатике

1.

Множества и логика
в задачах ЕГЭ по информатике
Докладчик: Денисов В.И.

2.

Задача 1
(Демо-2018). Для какого наибольшего целого числа А формула
( (x 9) (x x A) ) ( (y y A) (y 9) )
тождественно истинна (то есть принимает значение 1 при
любых целых неотрицательных значениях переменных x и y)?
1. Заменим импликацию на дизъюнкцию: А B= ¬A v B.
Получим: ( (x > 9) v (x x A) ) ( (y y > A) v (y 9) )
2. Чтобы формула была истинна:
(x > 9) v (x x A)=1
(y y > A) v (y 9)=1

3.

Задача 1
(Демо-2018). Для какого наибольшего целого числа А формула
( (x 9) (x x A) ) ( (y y A) (y 9) )
тождественно истинна (то есть принимает значение 1 при
любых целых неотрицательных значениях переменных x и y)?
3. Рассмотрим оба выражения по отдельности.
(x > 9) v (x x A)=1
A>=81
Интервал от 10 и далее закрывает неравенство x > 9.
Чтобы выражение было истинно для любых целых
неотрицательных x, для х<=9 должно выполнятся
неравенство x x A, это достижимо при A>=81

4.

Задача 1
(Демо-2018). Для какого наибольшего целого числа А формула
( (x 9) (x x A) ) ( (y y A) (y 9) )
тождественно истинна (то есть принимает значение 1 при
любых целых неотрицательных значениях переменных x и y)?
3. Аналогично для второго выражения:
(y y > A) v (y 9) = 1
A<100
Интервал до 9 включительно закрывает неравенство у<=9.
Чтобы выражение было истинно для любых целых
неотрицательных y , для y>9 должно выполнятся
неравенство y y > A, это достижимо при A < 100
Ответ : 99

5.

Задача 2
Известно, что для некоторого отрезка А формула
( (x A) (x2 64) ) ( (x2 25) (x A) )
тождественно истинна (то есть принимает значение 1 при
всех вещественных значениях переменной x). Какую
наименьшую длину может иметь отрезок A?
1. Заменим импликацию на дизъюнкцию: А B= ¬A v B.
Получим: ( (x A) v (x2 64) ) ( (x2 >25) v (x A) )
2. Чтобы формула была истинна:
(x A) v (x2 64) = 1
(x2 >25) v (x A) = 1

6.

Задача 2
Известно, что для некоторого отрезка А формула
( (x A) (x2 64) ) ( (x2 25) (x A) )
тождественно истинна (то есть принимает значение 1 при
всех вещественных значениях переменной x). Какую
наименьшую длину может иметь отрезок A?
3. Рассмотрим оба выражения по отдельности.
(x A) v (x2 64)=1
При x [-8;8]
выражение истинно
-8
8
x
При x [-8;8]
A max = [-8;8]
Это значит, что если x принадлежит отрезку A, должно
выполняться условие x2 64

7.

Задача 2
Известно, что для некоторого отрезка А формула
( (x A) (x2 64) ) ( (x2 25) (x A) )
тождественно истинна (то есть принимает значение 1 при
всех вещественных значениях переменной x). Какую
наименьшую длину может иметь отрезок A?
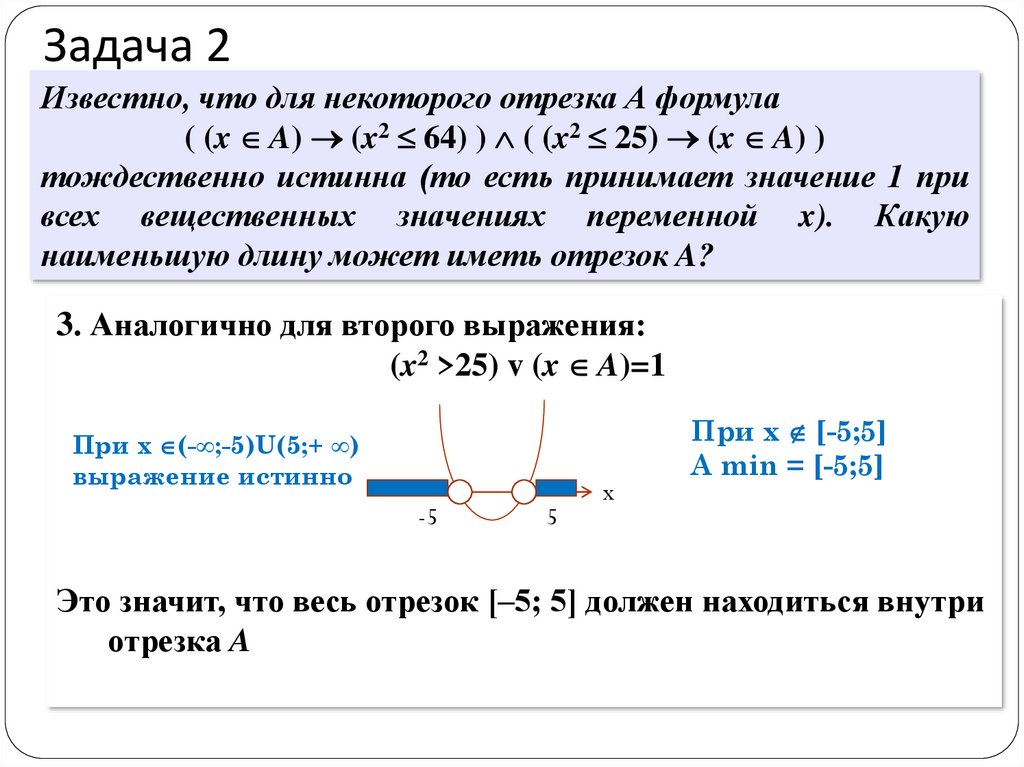
3. Аналогично для второго выражения:
(x2 >25) v (x A)=1
При x (-∞;-5)U(5;+ ∞)
выражение истинно
-5
5
x
При x [-5;5]
A min = [-5;5]
Это значит, что весь отрезок [–5; 5] должен находиться внутри
отрезка A

8.

Задача 2
Известно, что для некоторого отрезка А формула
( (x A) (x2 64) ) ( (x2 25) (x A) )
тождественно истинна (то есть принимает значение 1 при
всех вещественных значениях переменной x). Какую
наименьшую длину может иметь отрезок A?
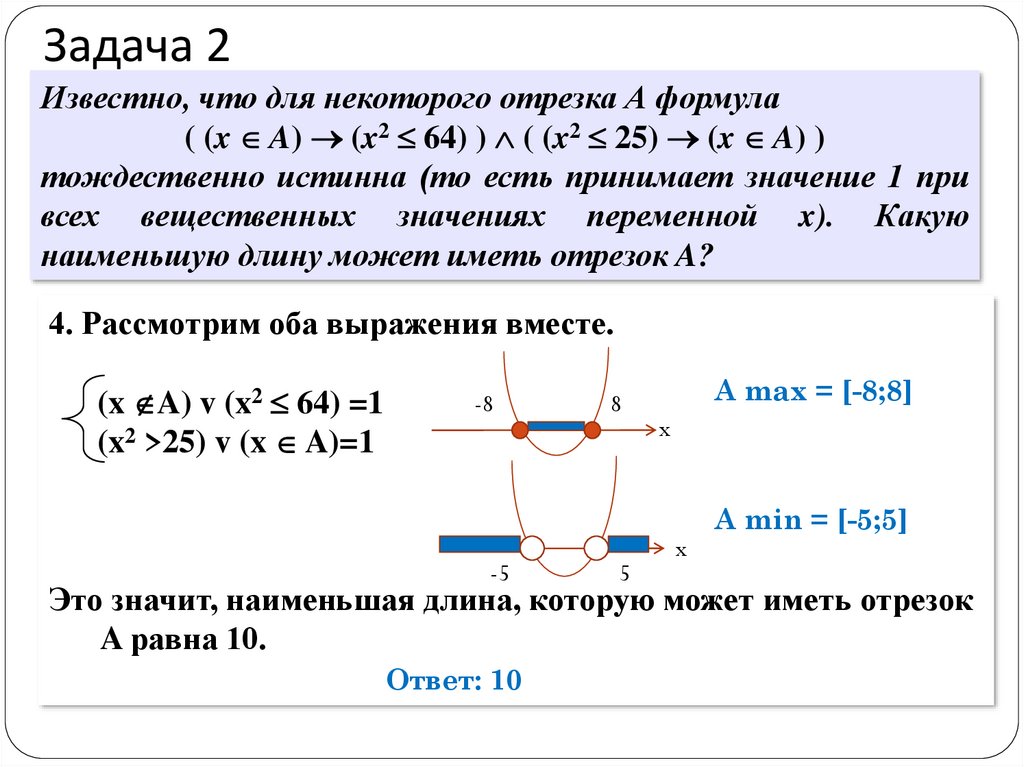
4. Рассмотрим оба выражения вместе.
(x A) v (x2 64) =1
(x2 >25) v (x A)=1
-8
8
A max = [-8;8]
x
A min = [-5;5]
-5
5
x
Это значит, наименьшая длина, которую может иметь отрезок
A равна 10.
Ответ: 10