Решение дифференциальных уравнений

1.

Решение дифференциальных
уравнений

2.

Рассмотрим численные методы решений задач с начальными
условиями (называемых задачами Коши) для обыкновенных
дифференциальных уравнений (далее используется сокращение
ОДУ). Такие задачи требуют нахождения функции (или нескольких
функций) одной переменной, если, во-первых, определено
дифференциальное уравнение (или система уравнений),
содержащее производную функции, и, во-вторых, необходимое
количество дополнительных условий, задающих значение
функции (функций) в некоторой начальной точке.
Решение задач Коши для ОДУ – давно и детально
разработанная технология. С «хорошими» ОДУ вообще никаких
вычислительных проблем обычно не возникает (чаще всего они
решаются при помощи алгоритма Рунге-Кутты), а для ОДУ
особого типа, называемых жесткими, необходимо применять
специальные методы. Все эти возможности заложены в Mathcad с
возможностью выбора конкретного алгоритма.

3.

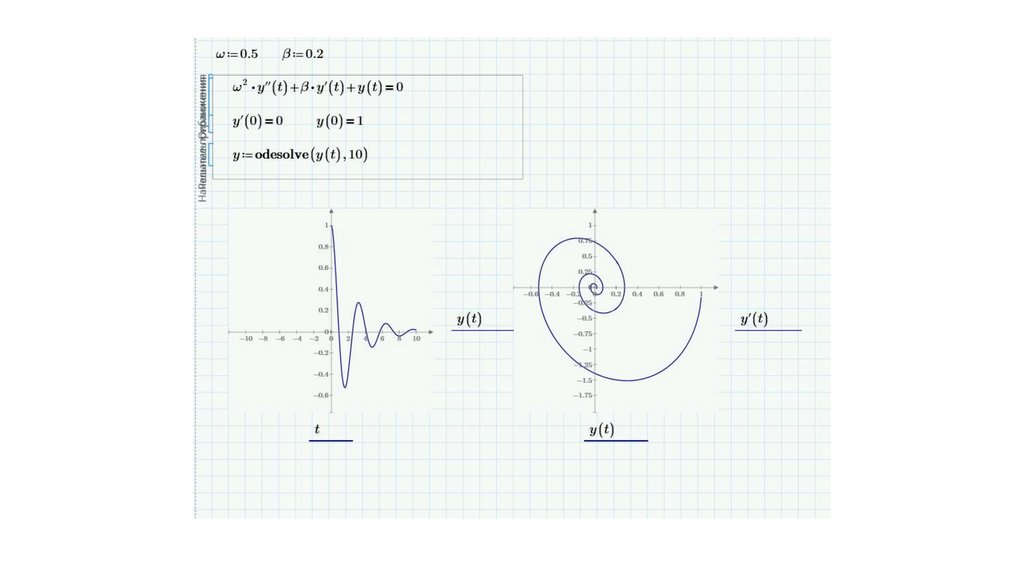
Рассмотрим решение простого ОДУ второго порядка,
описывающего модель затухающего гармонического осциллятора.
Модель гармонического осциллятора описывает, в частности,
колебания маятника: