Построение усеченной призмы

1.

ПОСТРОЕНИЕ
УСЕЧЕННОЙ
ПРИЗМЫ

2.

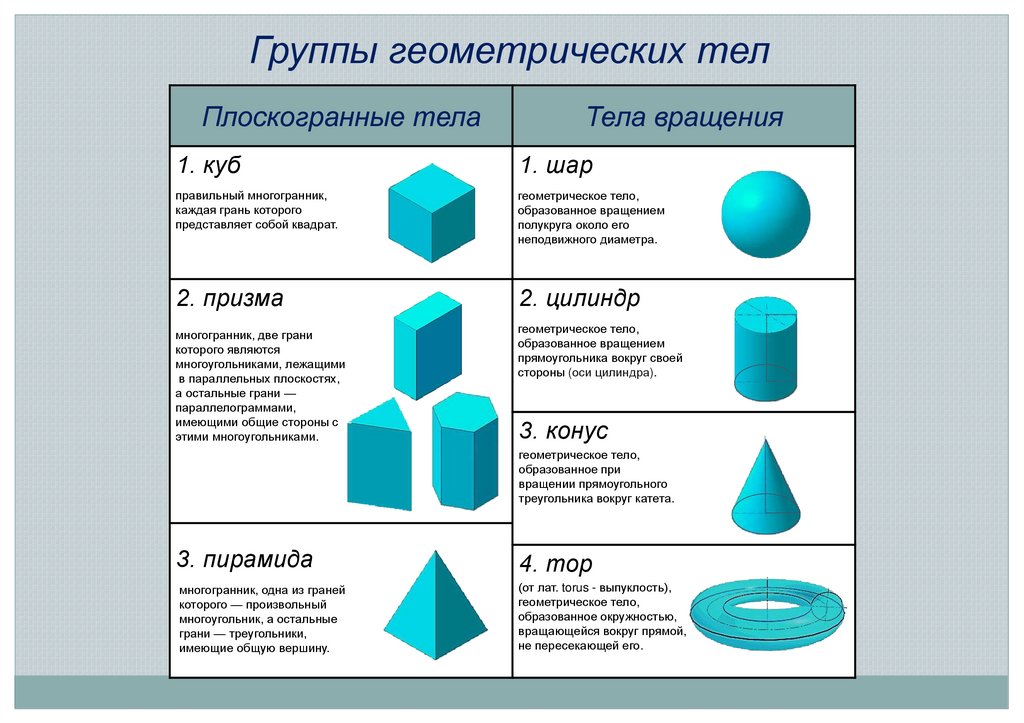
Группы геометрических тел
Плоскогранные тела
Тела вращения
1. куб
1. шар
правильный многогранник,
каждая грань которого
представляет собой квадрат.
геометрическое тело,
образованное вращением
полукруга около его
неподвижного диаметра.
2. призма
2. цилиндр
многогранник, две грани
которого являются
многоугольниками, лежащими
в параллельных плоскостях,
а остальные грани —
параллелограммами,
имеющими общие стороны с
этими многоугольниками.
геометрическое тело,
образованное вращением
прямоугольника вокруг своей
стороны (оси цилиндра).
3. конус
геометрическое тело,
образованное при
вращении прямоугольного
треугольника вокруг катета.
3. пирамида
4. тор
многогранник, одна из граней
которого — произвольный
многоугольник, а остальные
грани — треугольники,
имеющие общую вершину.
(от лат. torus - выпуклость),
геометрическое тело,
образованное окружностью,
вращающейся вокруг прямой,
не пересекающей его.

3.

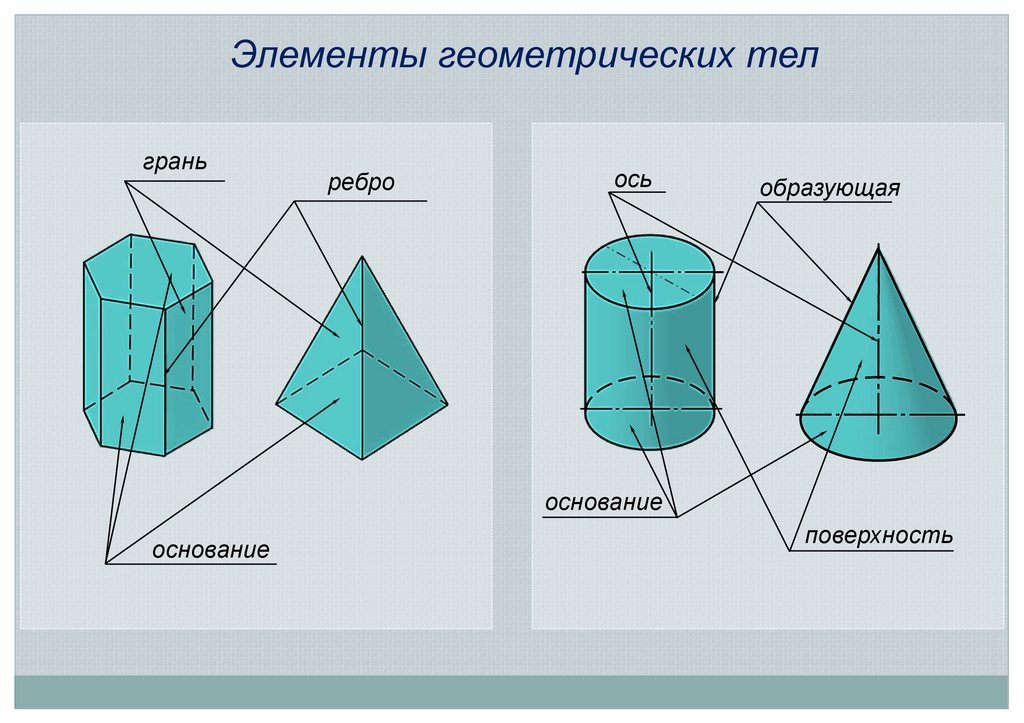
Элементы геометрических тел
грань
ребро
ось
образующая
основание
основание
поверхность

4.

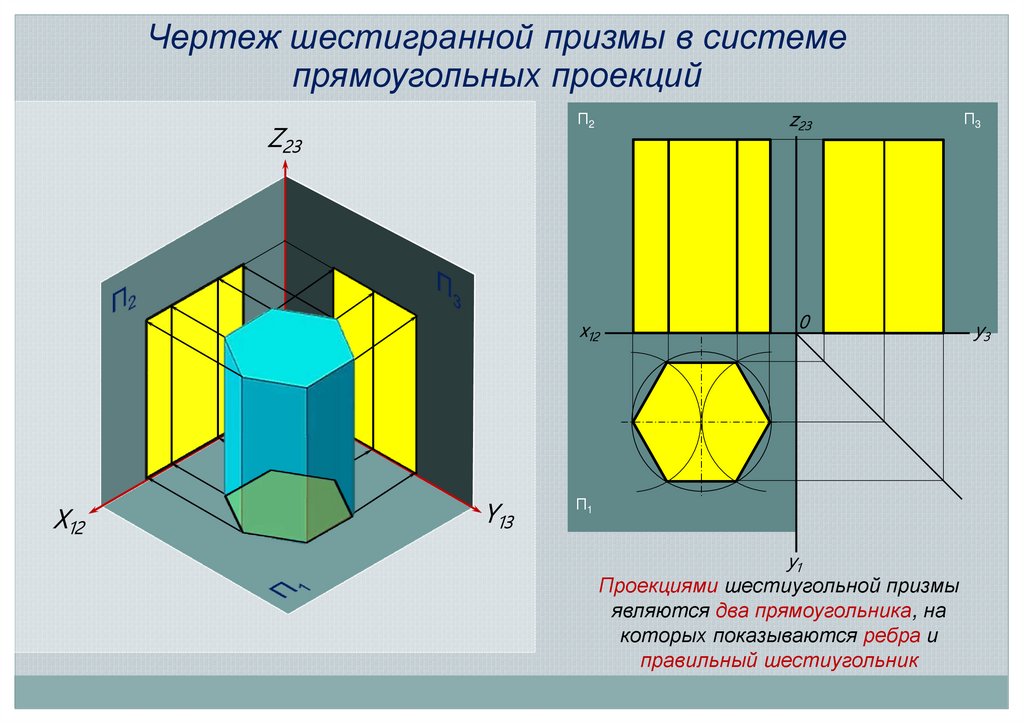
Чертеж шестигранной призмы в системе
прямоугольных проекций
z23
П2
Z23
х12
Х12
Y13
0
П1
y1
Проекциями шестиугольной призмы
являются два прямоугольника, на
которых показываются ребра и
правильный шестиугольник
П3
y3

5.

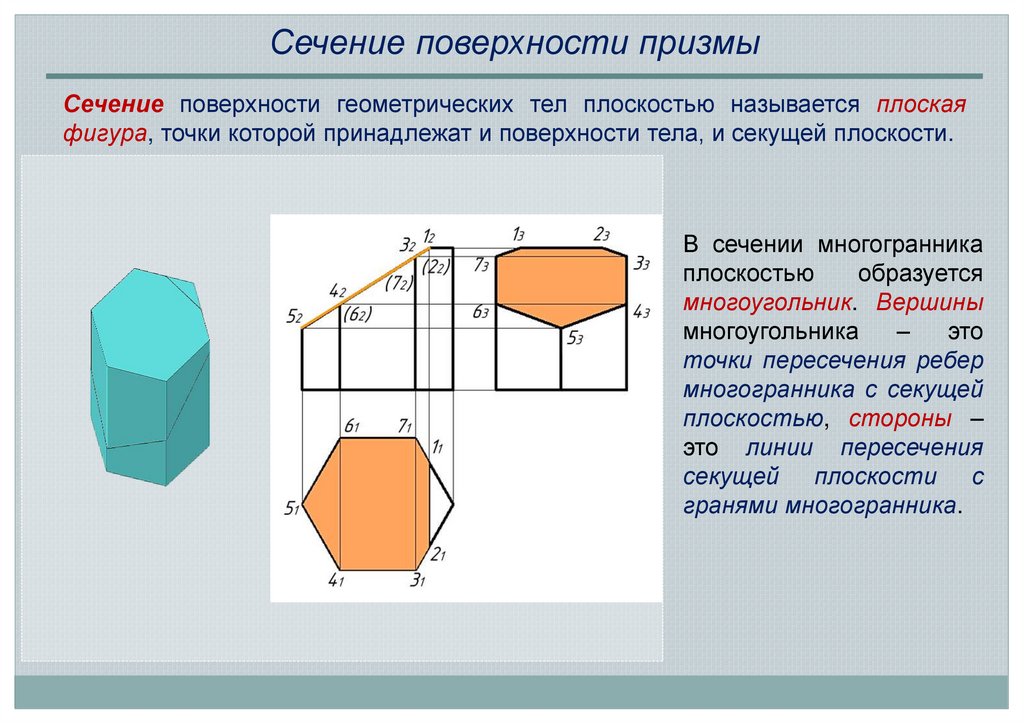
Сечение поверхности призмы
Сечение поверхности геометрических тел плоскостью называется плоская
фигура, точки которой принадлежат и поверхности тела, и секущей плоскости.
В сечении многогранника
плоскостью
образуется
многоугольник. Вершины
многоугольника
–
это
точки пересечения ребер
многогранника с секущей
плоскостью, стороны –
это линии пересечения
секущей плоскости с
гранями многогранника.

6.

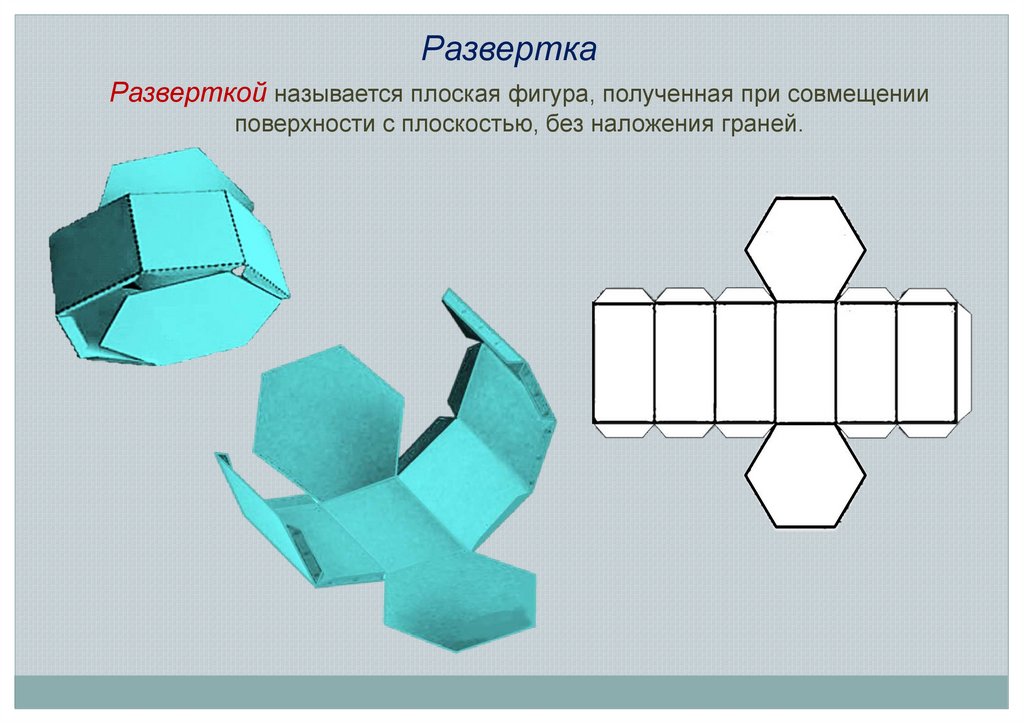
Развертка
Разверткой называется плоская фигура, полученная при совмещении
поверхности с плоскостью, без наложения граней.

7.

Задание:
1. Построить комплексный чертеж усеченной
призмы.
2. Найти действительную величину контура
сечения.
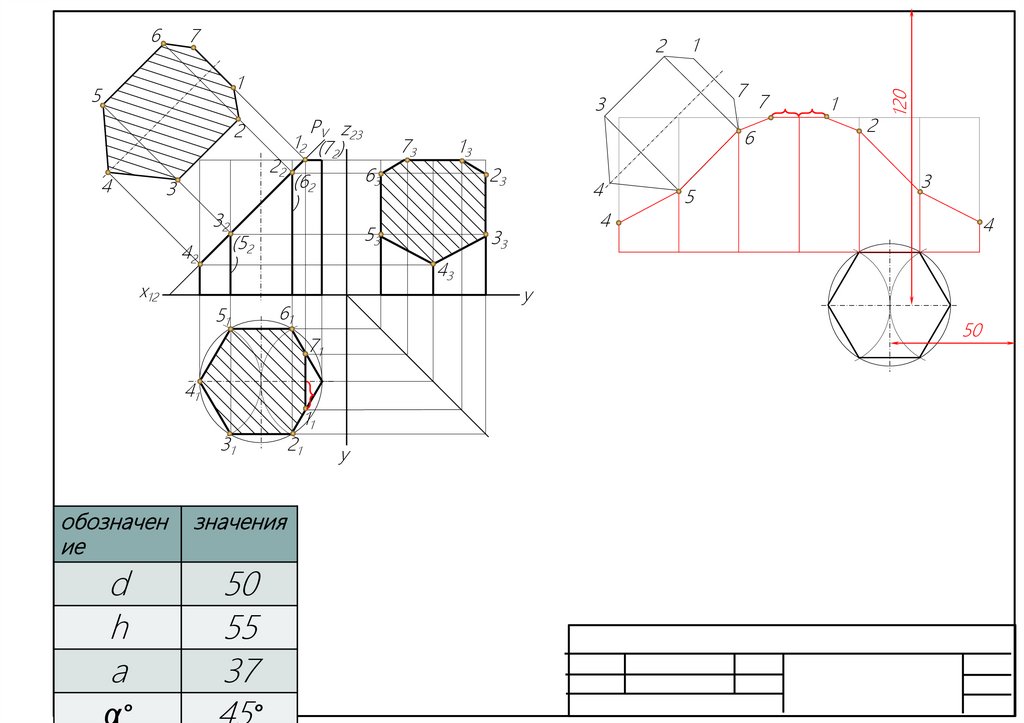
3. Построить развертку поверхности
усеченной призмы и аксонометрическую
проекцию.
Алгоритм построения
усечённого многогранника
1. Выполнить комплексный чертеж
многогранника.
обозначен
ие
значения
d
h
a
50
55
37
45°
α°
2. Построить след секущей плоскости.
3. Построить проекции фигуры
сечения на всех плоскостях проекций.
4. Обвести усечённую призму
сплошной основной линией

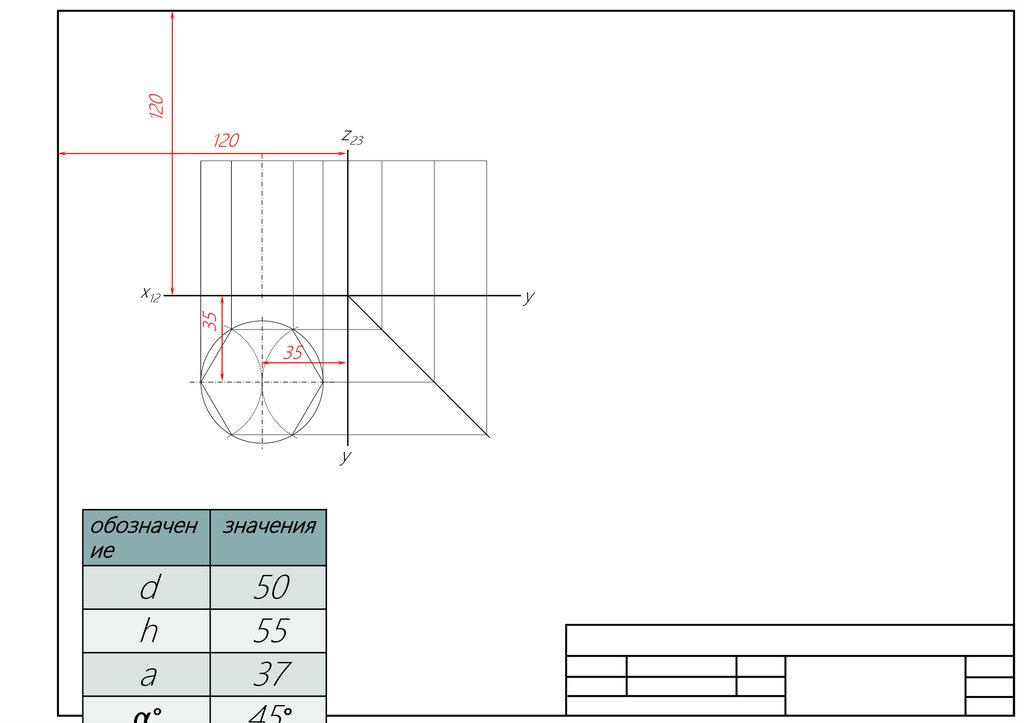
8.

120
z23
120
х12
35
y
35
12
y
обозначен
ие
значения
d
h
a
50
55
37

9.

PV z
23
45°
х12
y
37
12
y
обозначен
ие
значения
d
h
a
50
55
37

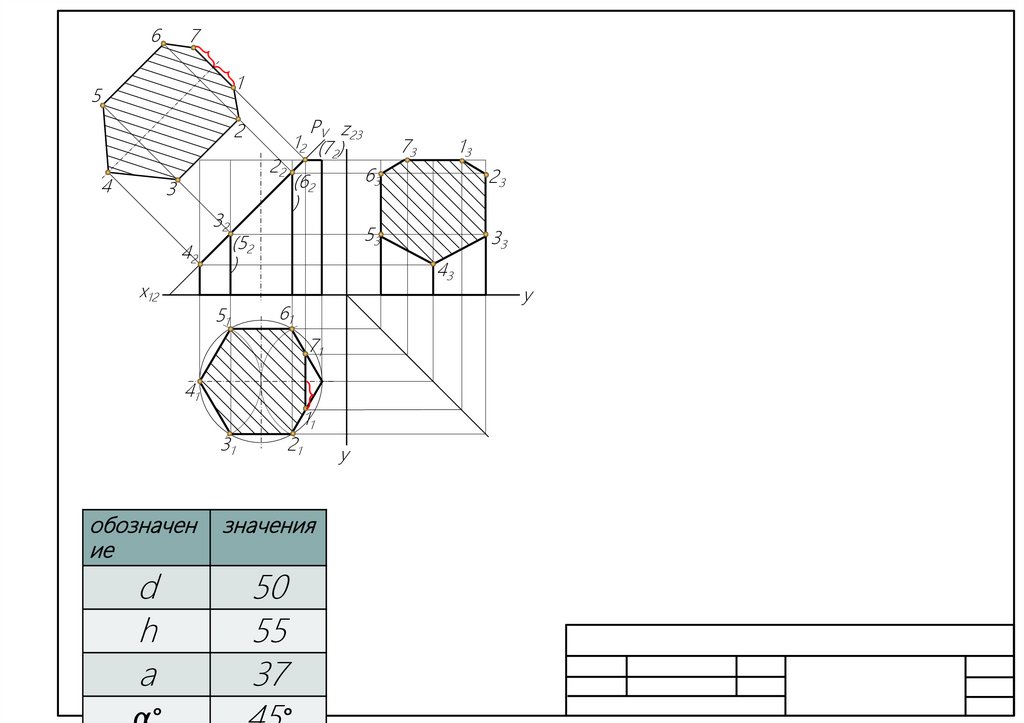
10.

PV z23
12 (7 )
2
22
32
42
(62
)
(52
)
х12
51
73
13
63
23
53
33
43
y
61
71
12
41
11
31
21
обозначен
ие
значения
d
h
a
50
55
37
y

11.

6
7
1
5
PV z23
12 (7 )
2
2
4
22
3
32
42
(62
)
(52
)
х12
51
73
13
63
23
53
33
43
y
61
71
12
41
11
31
21
обозначен
ие
значения
d
h
a
50
55
37
y

12.

7
2
1
1
5
7
3
PV z23
12 (7 )
2
2
4
22
3
32
42
51
6
13
63
(62
)
23
53
(52
)
х12
73
4
5
7
1
2
120
6
3
4
33
4
43
y
61
50
71
12
41
11
31
обозначен
ие
значения
d
h
a
50
55
37
21
y

13.

6
7
3
1
1
5
4
22
3
32
42
51
73
6
13
23
63
(62
)
53
(52
)
х12
2
PV z23
12 (7 )
2
2
7
4
4
33
5
7
1
3
2
4
43
y
61
71
12
41
11
31
21
обозначен
ие
значения
d
h
a
50
55
37
y
УСЕЧЕННАЯ ПРИЗМА

14.

6
7
1
2
1
5
4
22
3
32
х12
51
73
23
53
1
7
2
6
13
63
(62
)
(52
)
42
3
PV z23
12 (7 )
2
2
7
4
3
5
4
33
4
43
y
61
6
71
7 z
1
12
2
41
11
31
21
y
5
3
обозначен
ие
значения
d
h
a
50
55
37
4
x
y

15.

6
7
1
3
1
5
7
2
PV z23
12 (7 )
2
2
4
22
3
32
42
51
23
53
1
6
13
63
(62
)
(52
)
х12
73
7
4
3
2
5
4
4
33
43
y
61
z
7
71
6
12
1
2
41
11
31
21
y
5
3
4
x
y
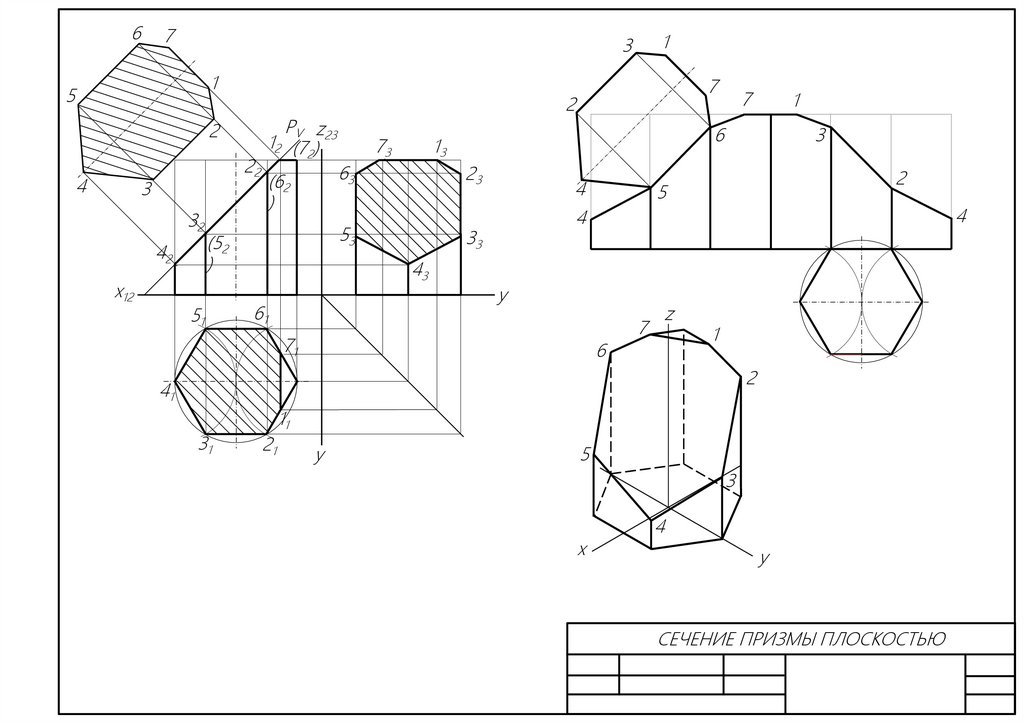
СЕЧЕНИЕ ПРИЗМЫ ПЛОСКОСТЬЮ