Similar presentations:
Методы оценки достоверности результатов статистического исследования
1.
ТЕМА 4.МЕТОДЫ ОЦЕНКИ
ДОСТОВЕРНОСТИ
РЕЗУЛЬТАТОВ
СТАТИСТИЧЕСКОГО
ИССЛЕДОВАНИЯ
2.
Методы оценки достоверности:Параметрические
(количественные
методы обработки данных, применение
которых требует обязательного знания
закона
распределения
изучаемых
признаков в совокупности и вычисления
их основных параметров);
Непараметрические
обязательного
распределения
совокупности).
(не
требуют
знания
закона
изучаемых признаков в
3.
ПАРАМЕТРИЧЕСКИЕ МЕТОДЫ
4.
Оценка достоверности(репрезентативности) результатов
исследования
- это погрешность, обусловленная переносом
результатов выборочного исследования на всю
генеральную совокупность.
Каждая средняя величина —
М (средняя
длительность лечения, средний рост, средняя
масса тела, средний уровень белка в крови и др.),
а также каждая относительная величина — Р
(уровень летальности, заболеваемости и др.)
должны быть представлены со своей средней
ошибкой (m).
5.
Ошибкарепрезентативности
Ошибка репрезентативности
(достоверности) (m) возникает в том
случае, если выборочная совокупность
не является репрезентативной, то есть
не отражает свойства генеральной
совокупности.
Т.е. чем больше ошибка
репрезентативности, тем слабее
выборочная совокупность отражает
генеральную.
6.
Средняя ошибка среднейарифметической величины
определяется по формуле:
где σ — среднее квадратическое отклонение;
n — число наблюдений.
7.
Средняя ошибка среднейарифметической величины
определяется по формуле:
где σ — среднее квадратическое отклонение;
n — число наблюдений.
Пример:
8.
Средняяошибка
относительной
величины
определяется по формуле:
где Р — относительная величина;
q — разность между основанием показателя и
самим показателем: так, если показатель
выражен в процентах, то q = 100 – Р, если Р
— в промилле, то q = 1000 – Р, если Р — в
продецимилле, то
q = 10 000 – Р и т. д.;
n — число наблюдений.
9.
Например: в группе иммунизированных (150чел.) заболело 42%,
в группе не иммунизированных против
гриппа (200 чел.) заболело 48%.
Рассчитаем средние ошибки относительных
величин по формуле:
10.
Например: в группе не иммунизированныхпротив гриппа (200 чел.) заболело 48%
. в группе иммунизированных (150 чел.)
заболело 42%,
Рассчитаем средние ошибки относительных
величин по формуле:
11.
При числе наблюдений менее 30средние ошибки репрезентативности
определяются по формулам:
12.
Определение доверительныхграниц
Доверительные границы — границы средних
(или относительных) величин, выход за пределы
которых вследствие случайных колебаний имеет
незначительную вероятность.
Т.е. это рамки, в которые с наибольшей
вероятностью
попадут
результаты
изучаемого явления.
Доверительная вероятность – вероятность
попадания средней или относительной величины
в этот интервал.
13.
Определение доверительных границДоверительные границы определяют по формулам:
где М ген и Р ген — соответственно значения средней
величины и относительного показателя в генеральной
совокупности;
М выб и Р выб — соответственно значения средней
величины и относительного показателя выборочной
совокупности;
m — ошибка репрезентативности;
t
—
критерий
достоверности
(доверительный
коэффициент, доверительный критерий).
14.
Определение доверительных границПроизведение t · m (Δ) - предельная ошибка
показателя, полученного при данном выборочном
исследовании.
Размеры
предельной
ошибки
зависят
от
коэффициента
t,
который
избирает
сам
исследователь, исходя из заданной вероятности
безошибочного прогноза (таблица Плохинского).
Величина критерия t связана с вероятностью
безошибочного
прогноза
(Р)
и
числом
наблюдений в выборочной совокупности.
15.
Вероятность безошибочногопрогноза
Для определения точности, с которой
исследователь желает получить результат, в
статистике используется понятие
вероятность безошибочного прогноза,
которая является характеристикой
надежности результатов выборочных
медико-биологических статистических
исследований.
16.
Доверительные границыДля большинства медико-биологических и
социальных исследований достоверными считаются
доверительные границы, установленные с
вероятностью безошибочного прогноза Р=95%, при
этом число случаев генеральной совокупности, в
котором могут наблюдаться отклонения от
закономерностей, установленных при выборочном
исследовании, не будут превышать 5% (t=2)
При ряде исследований, связанных, например, с
применением вакцин, оперативного лечения, в
результате чего возможны тяжелые заболевания,
осложнения, летальные исходы, применяется степень
вероятности Р=99,7%, т.е. не более чем у 1% случаев
генеральной совокупности возможны отклонения от
закономерностей, установленных в выборочной
совокупности. (t=3)
17.
при Р = 95%, t = 2.М ген = M + t * m =
7.87 + 2 × 0.18 = 7.87 + 0.36 = 7.51 - 8.23
(дней)
Следовательно, с вероятностью безошибочного
прогноза равной 95% можно утверждать, что
в
генеральной
совокупности
средняя
длительность лечения больных ангиной
будет находиться в пределах от 7.51 до 8,23
дней.
Несмотря на то, что мы не узнали «истинное»
значение средней длительности лечения
пациентов, мы с долей вероятности в 95%
можем сказать, что оно находится в пределах
от 7.51 до 8,23 дней.
18.
Зависимость доверительного критерия t отстепени вероятности безошибочного
прогноза Р (при n > 30)
Степень
вероятности
безошибочног
о прогноза (P
%)
Степень
вероятности
ошибки
прогноза (p,
%)
95,0 (0,95)
5% (0,05)
99,0 (0,99)
1% (0,01)
99,9 (0,999) 0,1% (0,001)
Доверите
льный
критерий
(t)
2
2,6
3,3
19.
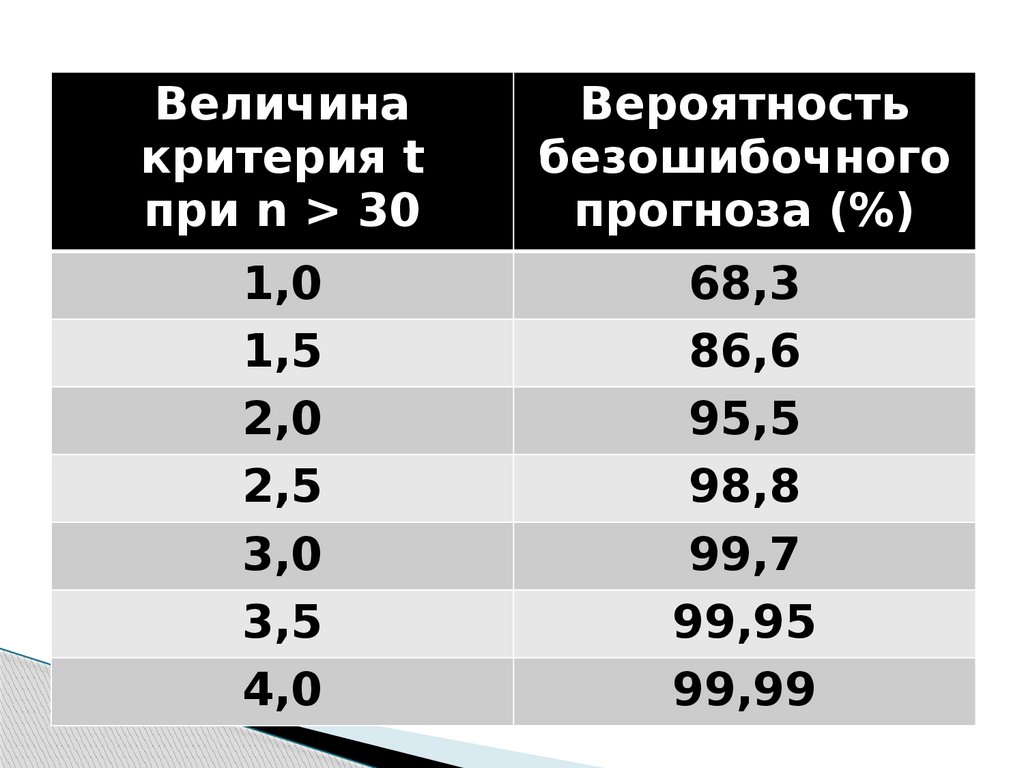
Величинакритерия t
при n > 30
Вероятность
безошибочного
прогноза (%)
1,0
1,5
2,0
2,5
3,0
3,5
4,0
68,3
86,6
95,5
98,8
99,7
99,95
99,99
20.
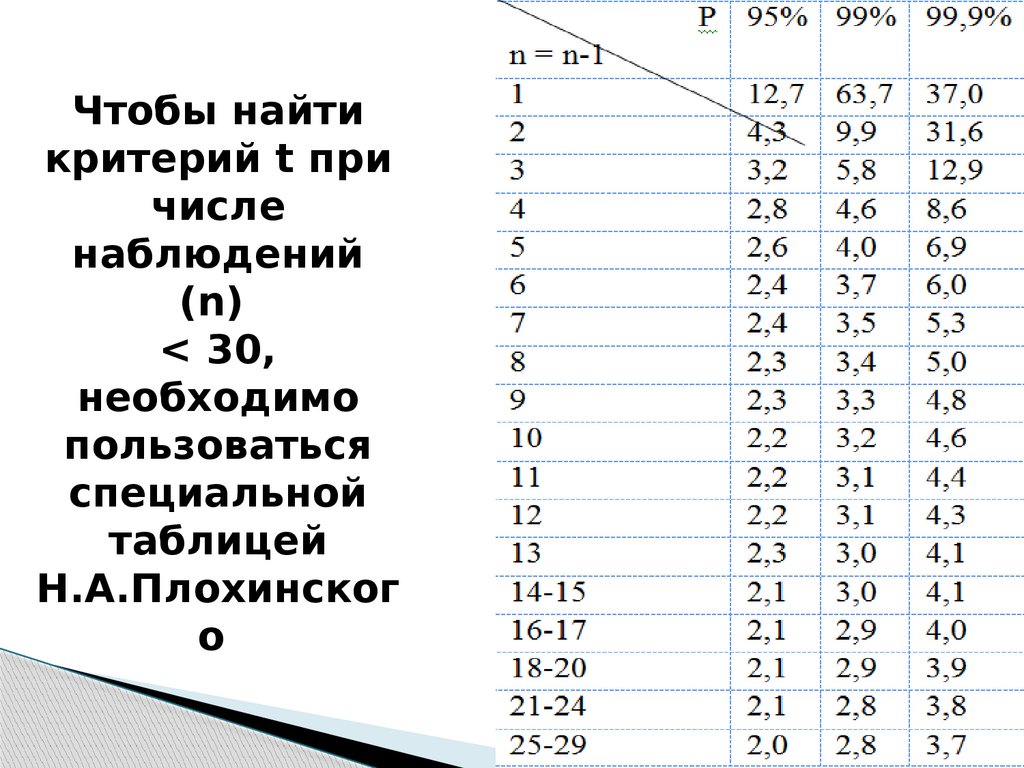
Чтобы найтикритерий t при
числе
наблюдений
(n)
< 30,
необходимо
пользоваться
специальной
таблицей
Н.А.Плохинског
о
21.
Оценка достоверности различий двухсредних или относительных величин по
t-критерию Стьюдента
Данный способ необходим, когда надо выяснить,
случайны ли различия между двумя средними
(или относительными показателями), или они
носят достоверный (существенный) характер.
Т.е., надо определить, различия между средними
или
относительными
величинами
имеют
случайный
характер,
или
же
разница
закономерна (т.е. носит закономерный характер).
Главное условие – наличие репрезентативности
между генеральной и выборочной совокупностью.
22.
Оценка достоверности различий двухсредних или относительных величин по
t-критерию Стьюдента
Формула
разности:
определения
достоверности
Разработан английским химиком У.Госсетом, (1908 г., публикация
в журнале «Биометрика» под псевдонимом «Student»)
где М1 и М2 — сравниваемые средние величины (P1
и P2, если сравниваются относительные величины) ;
m1 и m2 ошибки репрезентативности;
23.
ОЦЕНКА ДОСТОВЕРНОСТИ РАЗЛИЧИЙДВУХ СРЕДНИХ ИЛИ ОТНОСИТЕЛЬНЫХ
ВЕЛИЧИН ПО t-КРИТЕРИЮ СТЬЮДЕНТА
Если t < 2 ⇒ p > 0,05 (5%) – различия
между
средними
статистически
не
значимы, прогноз не подтвержден (т.е.
разница не достоверна, носит случайный
характер)
Если t ≥ 2 ⇒ p < 0,05 (5%) – различия
между средними статистически значимы,
прогноз
подтвержден
(разница
достоверна,
носит
закономерный
характер, обусловлена влиянием какогото определенного фактора
24.
ОПРЕДЕЛЕНИЕ ДОСТОВЕРНЫХ РАЗЛИЧИЙМЕЖДУ
ДВУМЯ СРЕДНИМИ ВЕЛИЧИНАМИ
Требуется определить, имеется ли достоверное снижение
частоты пульса и приближение ее к норме в группе
студентов после экзаменов, если известно, что средняя
частота пульса (М1) до экзамена составила 98,8 удара в
минуту (m1 = 4 уд./мин); после экзамена (М2) — 84 удара в
минуту (m2 = 5 уд./мин).
Достоверность
разности между средними величинами
определяется по формуле:
25.
ОПРЕДЕЛЕНИЕ ДОСТОВЕРНЫХ РАЗЛИЧИЙМЕЖДУ
ДВУМЯ СРЕДНИМИ ВЕЛИЧИНАМИ
Вывод. Поскольку t > 2 , то с вероятностью
безошибочного прогноза свыше 95%
можно утверждать, что после экзамена
частота пульса у студентов снижается и
приближается к норме. Т.е. снижение
имеет закономерный характер.
26.
Требуетсяопределить,
имеется
ли
достоверное
снижение
частоты
заболеваемости гриппом, если известно,
что в группе неиммунизированных (P ) до
заболело 48% (m1 = 3,5%); в группе
иммунизированных (P ) — 42% (m2 =
4%).
1
2
27.
Посколькуt
<
2,
следовательно,
отсутствуют достоверные различия между
показателями заболеваемости в группах
иммунизированных и
неиммунизированных лиц, что говорит о
неэффективности иммунизации против
гриппа. Т.е. изменения несут случайный
характер.
28.
НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ
29.
Непараметрическиеметоды
оценки
достоверности
используются для сравнения не
только по количественным, но и
по качественным признакам,
которые
нельзя
выразить
количественно
(не
имеют
числового
представления),
но
можно ранжировать.
30.
Длятого,
чтобы
доказать
некое
утверждение,
выдвинем
«НУЛЕВУЮ
ГИПОТЕЗУ»,
которую
в
процессе
исследования попытаемся опровергнуть
(или подтвердить).
Нулевая гипотеза широко используется для
доказательства при оценке достоверности
различия между сравниваемыми группами
по критерию соответствия (хи-квадрат χ2)
31.
Хи-квадратχ2
-
критерий соответствия.
Применяется
для
оценки
распределения
эмпирических вариационных рядов
и для
доказательства достоверности различий между
несколькими выборочными совокупностями.
Этот показатель применяется в том случае, если
результаты представлены абсолютными числами
и результат исхода имеет несколько градаций
(выздоровел, состояние улучшилось, состояние
ухудшилось, состояние не изменилось, умер).
32.
Критерийоснован на нулевой
гипотезе об ОТСУТСТВИИ разницы
между величинами.
Чем
больше
фактические
величины
отличаются
от
ожидаемых,
тем
больше
вероятность,
что
отличие
достоверно
и
есть
влияние
изучаемого фактора.
33.
Критерий вычисляется по формуле:Где
ф – фактическое число в каждой
группе,
ф1 – ожидаемое число в каждой группе,
34.
Далее определяют число степенейсвободы по формуле:
n = (S - 1)*(R - 1),
Где S – число строк, а R – число
столбцов.
35.
Полученнуювеличину оцениваем по
таблице критических значений для χ2 ,
полученная
величина
χ2
≥
табличного
значения
для
данной
степени свободы, то нулевая гипотеза
опровергается.
Если
полученная
величина
χ2
<
табличного
значения
для
данной
степени свободы, то нулевая гипотеза
подтверждается.
Если
36.
Рассчитаемвлияние
проведения
противогриппозной
вакцинации
на
заболеваемость гриппом.
Всег
о
Вакциниро
ваны
Не
вакциниро
ваны
Сумма
Фактическое (ф)
Заболело
73
Не
заболело
54
21
7
14
94
61
33
19
37.
1этап. Формируем нулевую гипотезу,
согласно которой
Введение
противогриппозной вакцины
не повлияло на заболеваемость гриппом.
В
этом
случае
распределение
на
заболевших и не заболевших в двух
группах должно быть одинаковым.
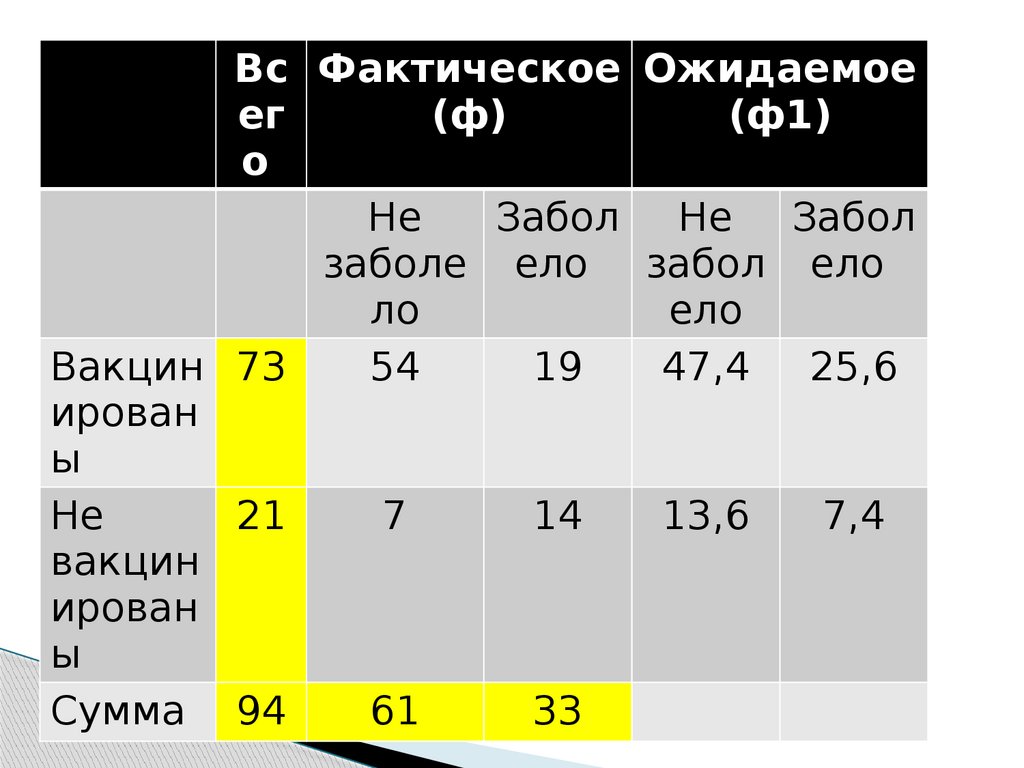
38.
Из 94 человек не заболел 61.Сколько
человек не заболеет из числа
вакцинированных
(73)
и
вакцинированных (21)?
Составим простую пропорцию.
94 → 61
73 → х
Х = (73*61)/94 = 47,4
39.
Вс Фактическое Ожидаемоеег
(ф)
(ф1)
о
Не
Забол Не Забол
заболе ело забол ело
ло
ело
Вакцин 73
54
19
47,4 25,6
ирован
ы
Не
21
7
14
13,6
7,4
вакцин
ирован
ы
Сумма 94
61
33
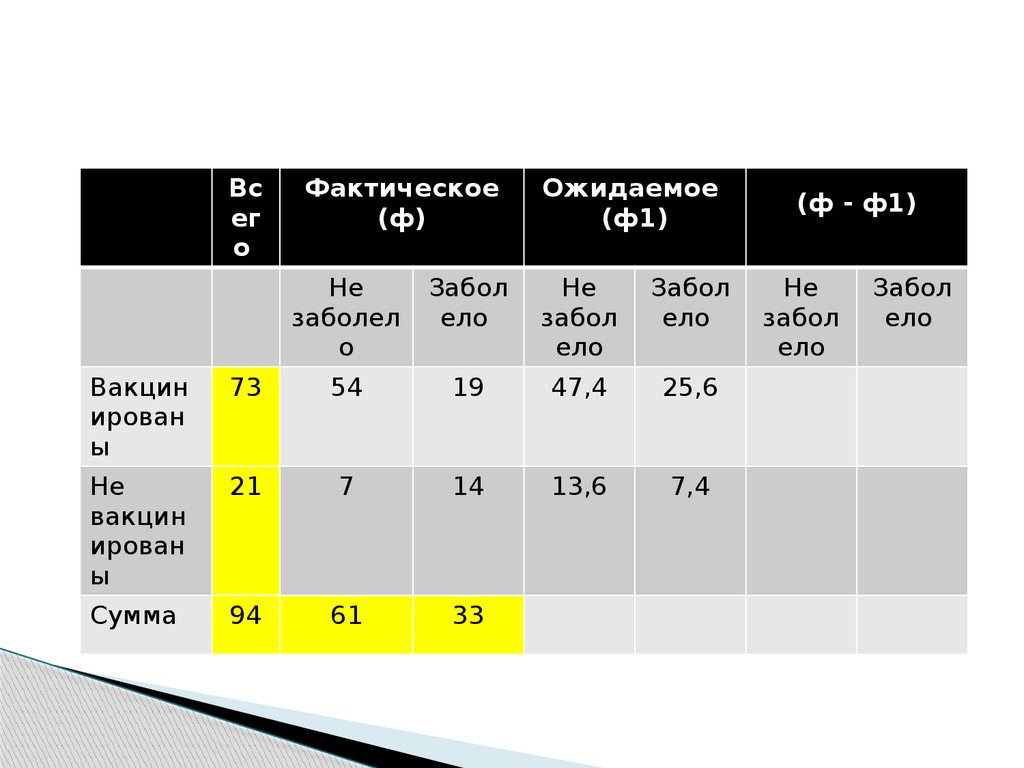
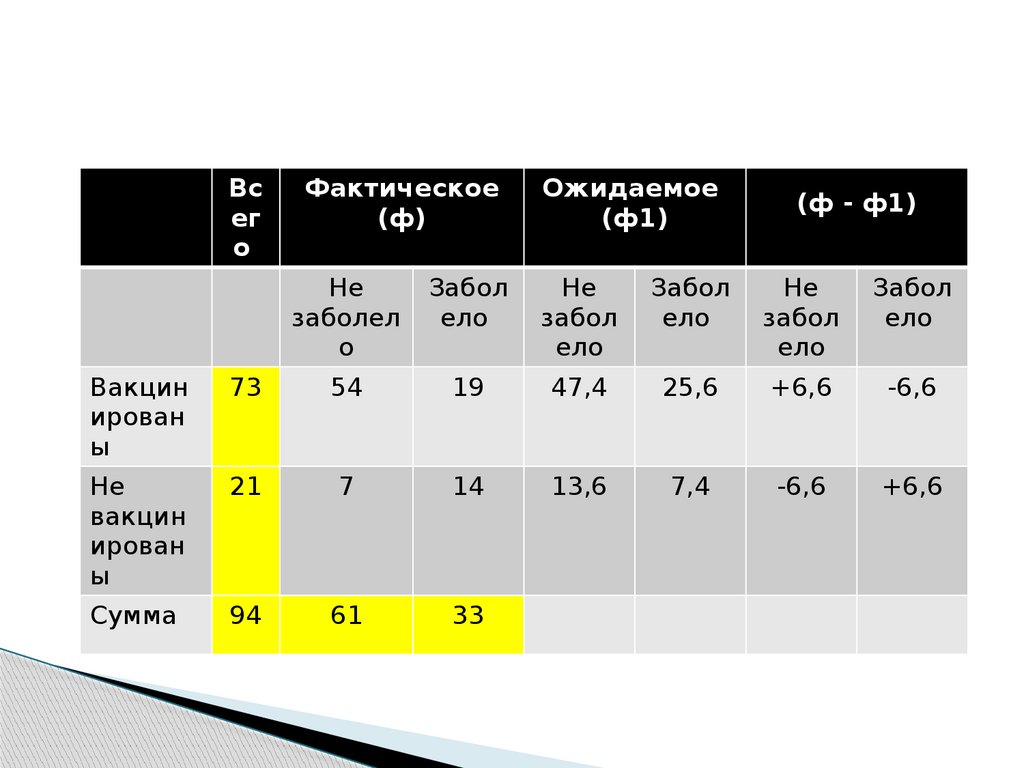
40.
Всег
о
Фактическое
(ф)
Ожидаемое
(ф1)
Не
заболел
о
Забол
ело
Не
забол
ело
Забол
ело
Вакцин
ирован
ы
73
54
19
47,4
25,6
Не
вакцин
ирован
ы
21
7
14
13,6
7,4
Сумма
94
61
33
(ф - ф1)
Не
забол
ело
Забол
ело
41.
Всег
о
Фактическое
(ф)
Ожидаемое
(ф1)
Не
заболел
о
Забол
ело
Не
забол
ело
Забол
ело
Не
забол
ело
Забол
ело
(ф - ф1)
Вакцин
ирован
ы
73
54
19
47,4
25,6
+6,6
-6,6
Не
вакцин
ирован
ы
21
7
14
13,6
7,4
-6,6
+6,6
Сумма
94
61
33
42.
Всег
о
Фактическое
(ф)
Ожидаемое
(ф1)
Не
заболе
ло
Забол
ело
Не
забол
ело
Забол
ело
Не
забол
ело
Забол
ело
(ф - ф1)
Вакцин
ирован
ы
73
54
19
47,4
25,6
+6,6
-6,6
Не
вакцин
ирован
ы
21
7
14
13,6
7,4
-6,6
+6,6
Сумма
94
61
33
(ф - ф1)2
Не
забол
ело
Забол
ело
43.
Всег
о
Фактическое
(ф)
Ожидаемое
(ф1)
Не
заболе
ло
Забол
ело
Не
забол
ело
Забол
ело
Не
забол
ело
Забол
ело
Не
забол
ело
Забол
ело
(ф - ф1)
(ф - ф1)2
Вакцин
ирован
ы
73
54
19
47,4
25,6
+6,6
-6,6
43,56
43,56
Не
вакцин
ирован
ы
21
7
14
13,6
7,4
-6,6
+6,6
43,56
43,56
Сумма
94
61
33
44.
Вс
е
г
о
Фактическ
ое (ф)
Ожидаем
ое
(ф1)
(ф - ф1)
(ф - ф1)2
(ф - ф1)2 /
ф1
Не
Забо Не Забо Не Забо Не Забо Не Забо
забол лело забо лело забо лело забо лело забо лело
ело
лело
лело
лело
лело
Вакц
инир
ован
ы
7
3
54
19
47,4
25,6
+6,6
-6,6
43,5
6
43,5
6
Не
вакци
ниров
аны
2
1
7
14
13,6
7,4
-6,6
+6,6
43,5
6
43,5
6
Сумм
а
9
4
61
33
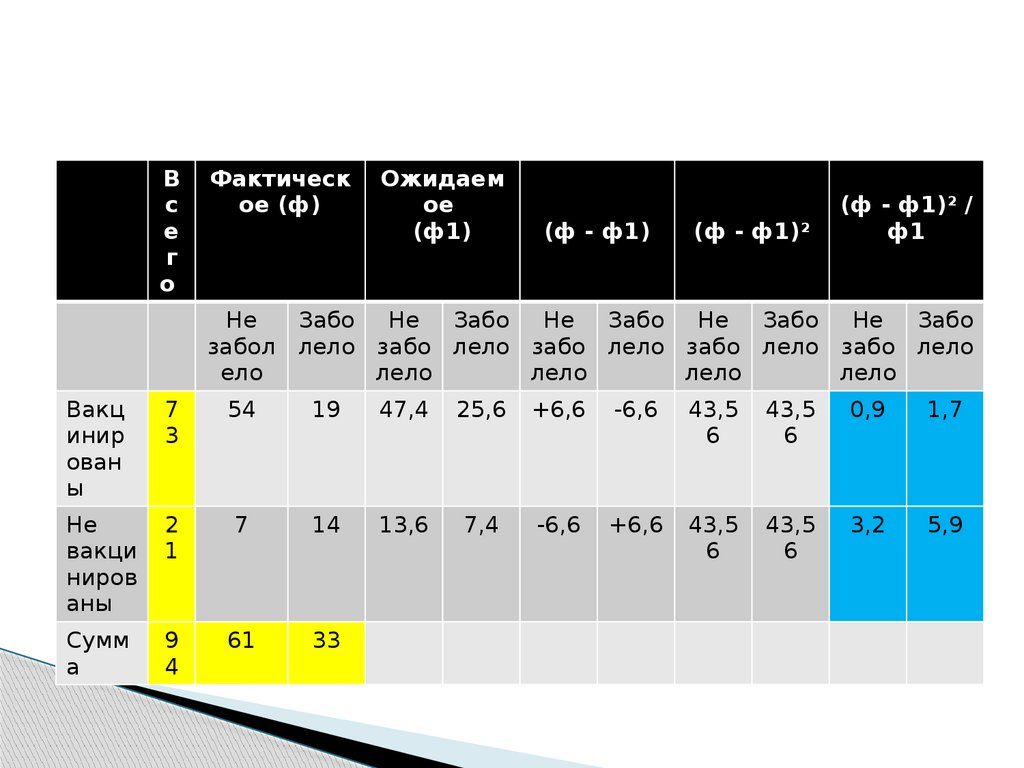
45.
Вс
е
г
о
Фактическ
ое (ф)
Ожидаем
ое
(ф1)
(ф - ф1)
(ф - ф1)2
(ф - ф1)2 /
ф1
Не
Забо Не Забо Не Забо Не Забо Не Забо
забол лело забо лело забо лело забо лело забо лело
ело
лело
лело
лело
лело
Вакц
инир
ован
ы
7
3
54
19
47,4
25,6
+6,6
-6,6
43,5
6
43,5
6
0,9
1,7
Не
вакци
ниров
аны
2
1
7
14
13,6
7,4
-6,6
+6,6
43,5
6
43,5
6
3,2
5,9
Сумм
а
9
4
61
33
46.
χ2 = 0,9 + 1,7 + 3,2 +5,9 = 11,7
n = (S - 1)*(R - 1)
n = (2-1) * (2-1) = 1
47.
χ2 = 11,7n = 1
48.
Таккак Х2 для данной степени свободы
больше табличного значения, значит,
нулевая гипотеза (о том, что вакцинация
не влияет на уровень заболеваемости),
оказалась
НЕСОСТОЯТЕЛЬНА,
т.е.
ОПРОВЕРГНУТА.
Это
значит, что введение вакцины
действительно оказывает влияние на
уровень заболеваемости гриппом.







































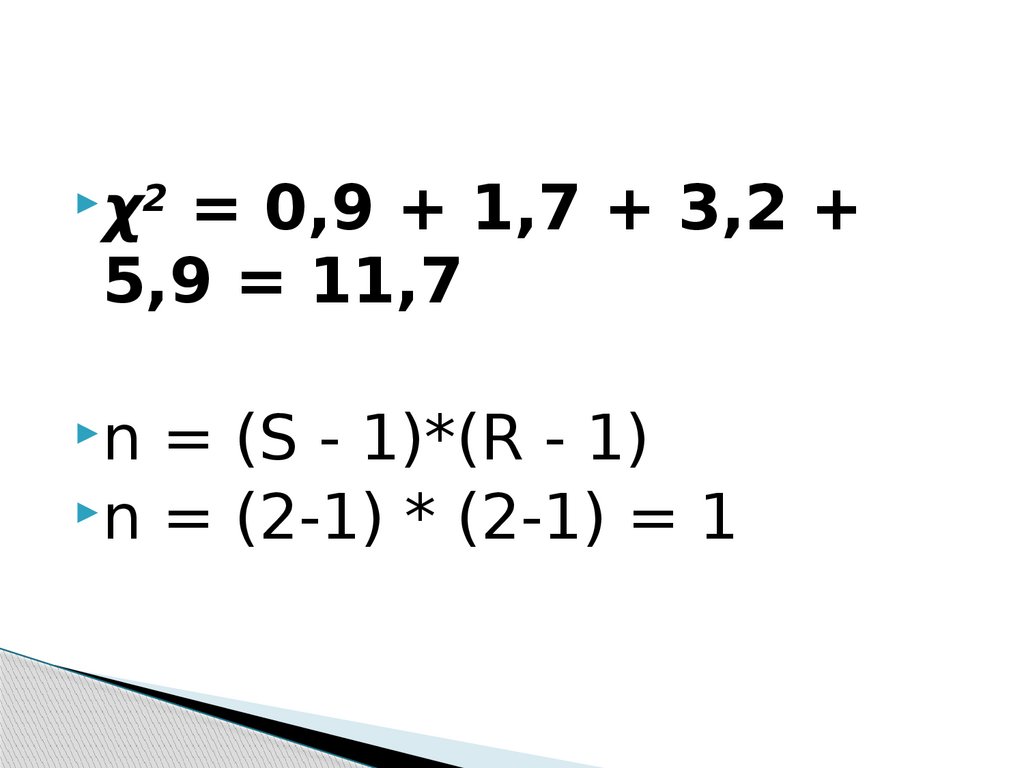



 sociology
sociology








