Similar presentations:
Робота та енергія. Закони збереження
1. Кафедра фізики ХНУРЕ
ФІЗИКАДоцент кафедри фізики ХНУРЕ
кандидат технічних наук,
Чубукін Олександр Сергійович
1
2. ЛЕКЦІЯ 3 Робота та енергія. Закони збереження
23.
ВступОдним з фундаментальних понять фізики є енергія.
Енергія
являє
собою
скалярну
фізичну
величину,
що
кількісно
характеризує різні форми руху матерії і відповідні їм взаємодії.
З різними формами руху матерії пов’язані різні види енергії:
Енергія - це фізична величина, яка характеризує здатність тіла або
3
системи тіл виконувати роботу
4.
РоботаПоняття робота вводиться щоб кількісно оцінити процес обміну
енергією між взаємодіючими тілами
Робота — це фізична величина, яка є мірою зміни енергії тіла
результаті дії на нього зовнішніх сил.
Механічна
робота – це фізична
величина, що характеризує процес, під
час якого сила F деформує або
переміщує тіло.
Тобто, поняття механічної роботи
пов’язано з поняттями сили й переміщення.
4
в
5.
Робота сталої сили при переміщені тіла удовжпрямолінійної ділянки траєкторії
Робота сталої сили (як за величиною, так за напрямком) при переміщенні
тіла удовж прямолінійної ділянки траєкторії є скалярною величиною, яка
дорівнює добутку проекції Fs сили на напрямок переміщення і переміщення S
A F s F s cos Fs s
Одиниця виміру роботи Джоуль:
[A] = [H·м] = [Дж]
Робота в 1 Дж – це робота, що виконується силою в 1 Н на
переміщенні в 1 м
5
6.
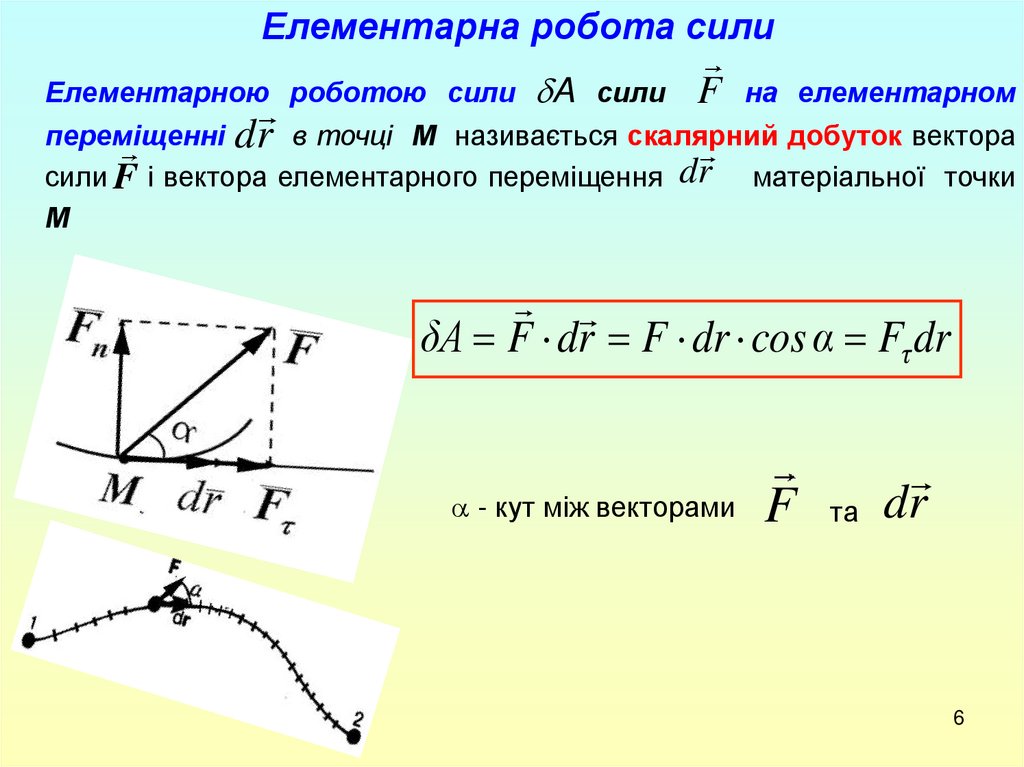
Елементарна робота силиЕлементарною роботою сили A сили
F на елементарном
переміщенні dr в точці М називається скалярний добуток вектора
сили F і вектора елементарного переміщення dr
М
матеріальної точки
δA F dr F dr cos α Fτ dr
- кут між векторами F та dr
6
7.
Робота на кінцевій ділянці траєкторіЯкщо матеріальна точка (тіло) М рухається по траєкторії, яка
розбита на елементарні ділянки, то при русі тіла М удовж довільної
траєкторії, сила F може змінюватися у кожній точці як за напрямком,
так і за величиною
Робота А, що виконується силою на
кінцевій ділянці траєкторі 1-2 дорівнює
алгебраїчній
сумі
робіт
на
всіх
елементарних
ділянках,
тобто
виражається криволінійним інтегралом
індекси 1 та 2 позначають початкову та
кінцеву точки траєкторії
В координатній формі:
2
2
2
1
1
1
A12 F dr F cos αdr Fτ dr
dr dxi dxj dzk
F Fxi Fy j Fz k
x2
y2
z2
A12 Fx dx Fy dy Fz dz
x1
y1
z1
7
8.
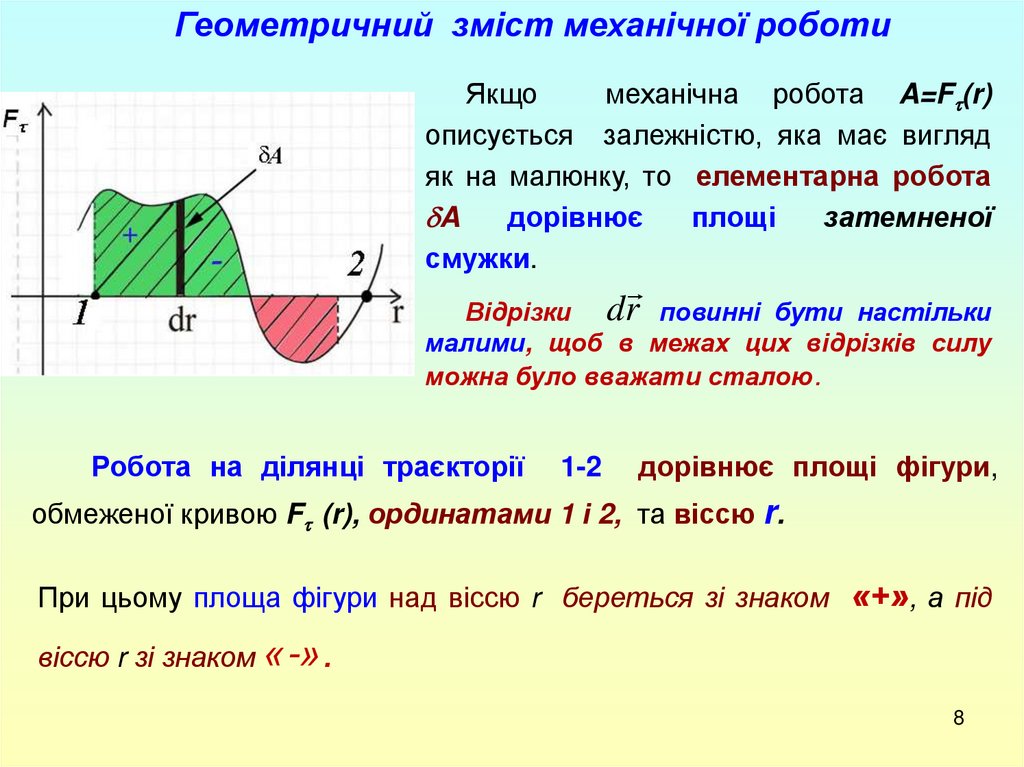
Геометричний зміст механічної роботиЯкщо
механічна робота A=F (r)
описується залежністю, яка має вигляд
як на малюнку, то елементарна робота
A
дорівнює
площі
затемненої
смужки.
dr повинні бути настільки
Відрізки
малими, щоб в межах цих відрізків силу
можна було вважати сталою.
Робота на ділянці траєкторії
1-2
дорівнює площі фігури,
обмеженої кривою F (r), ординатами 1 і 2, та віссю r.
При цьому площа фігури над віссю r береться зі знаком «+», а під
віссю r зі знаком «-».
8
9.
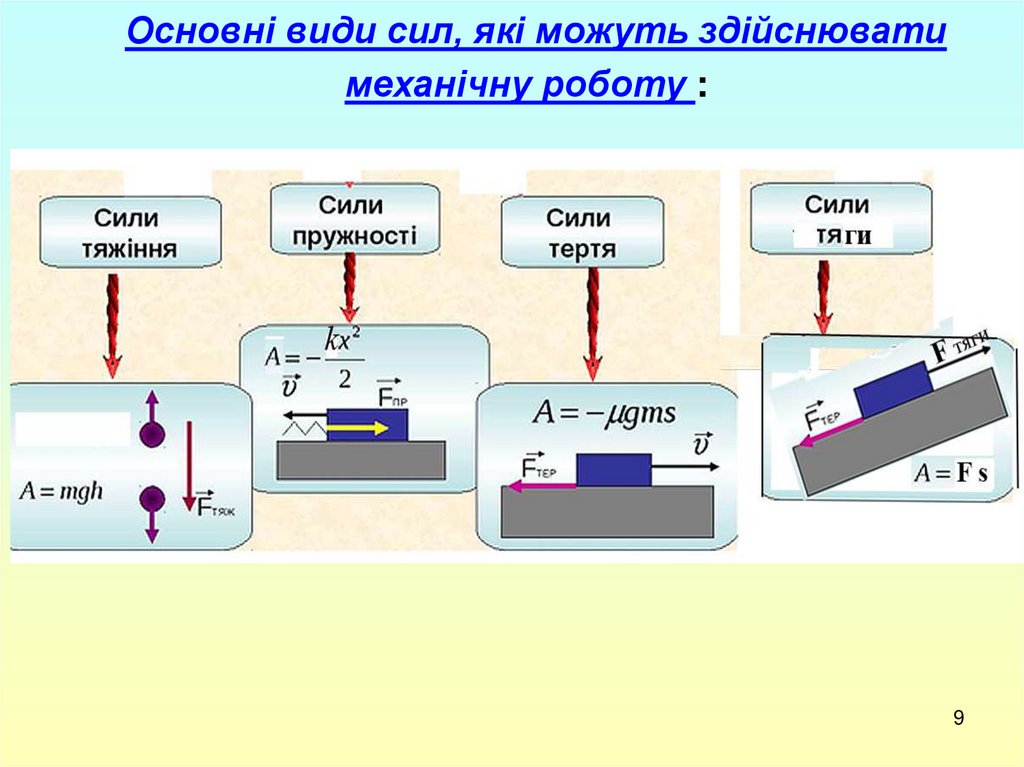
Основні види сил, які можуть здійснюватимеханічну роботу :
9
10.
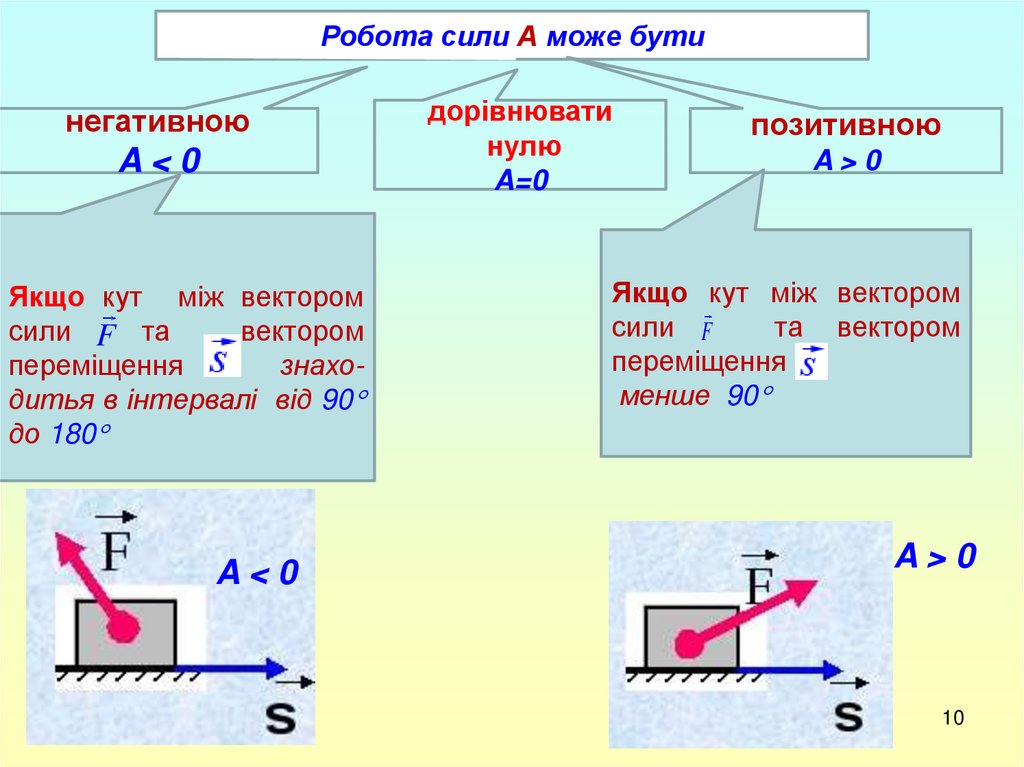
Робота сили А може бутинегативною
A<0
Якщо кут між вектором
сили F та
вектором
переміщення
знаходитья в інтервалі від 90
до 180
A<0
дорівнювати
нулю
A=0
позитивною
A>0
Якщо кут між вектором
сили F
та вектором
переміщення
менше 90
A>0
10
11.
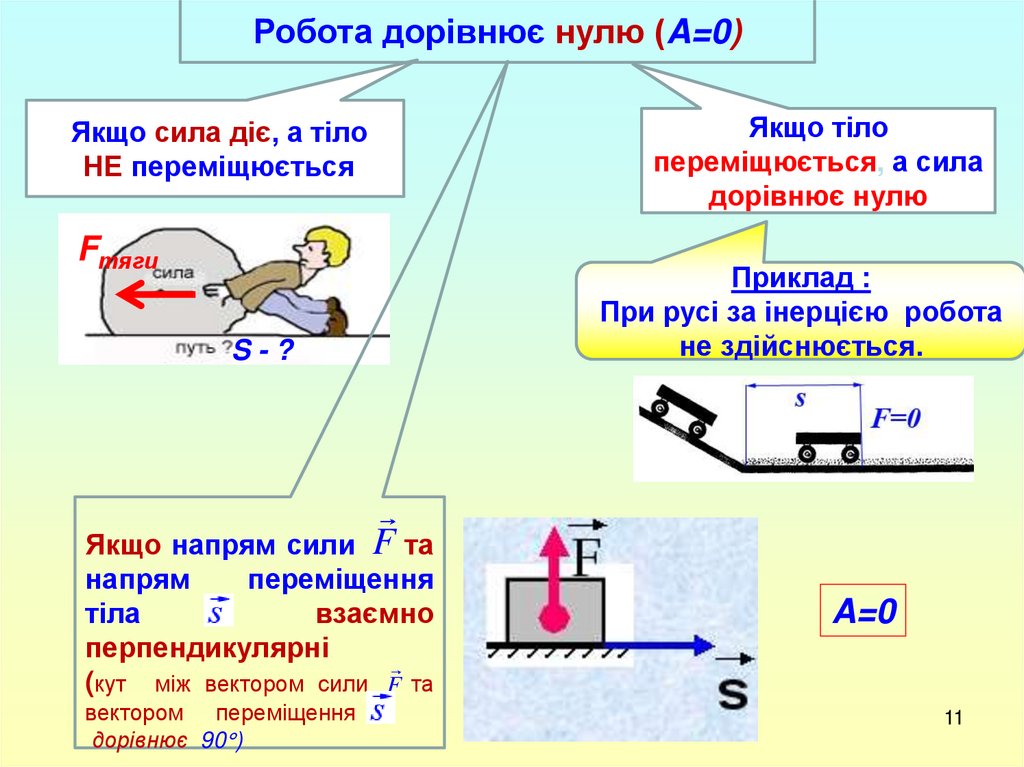
Робота дорівнює нулю (A=0)Якщо сила діє, а тіло
НЕ переміщюється
Fтяги
S-?
Якщо напрям сили F та
напрям
переміщення
тіла
взаємно
перпендикулярні
(кут між вектором сили F та
вектором переміщення
дорівнює 90 )
Якщо тіло
переміщюється, а сила
дорівнює нулю
Приклад :
При русі за інерцією робота
не здійснюється.
A=0
11
12.
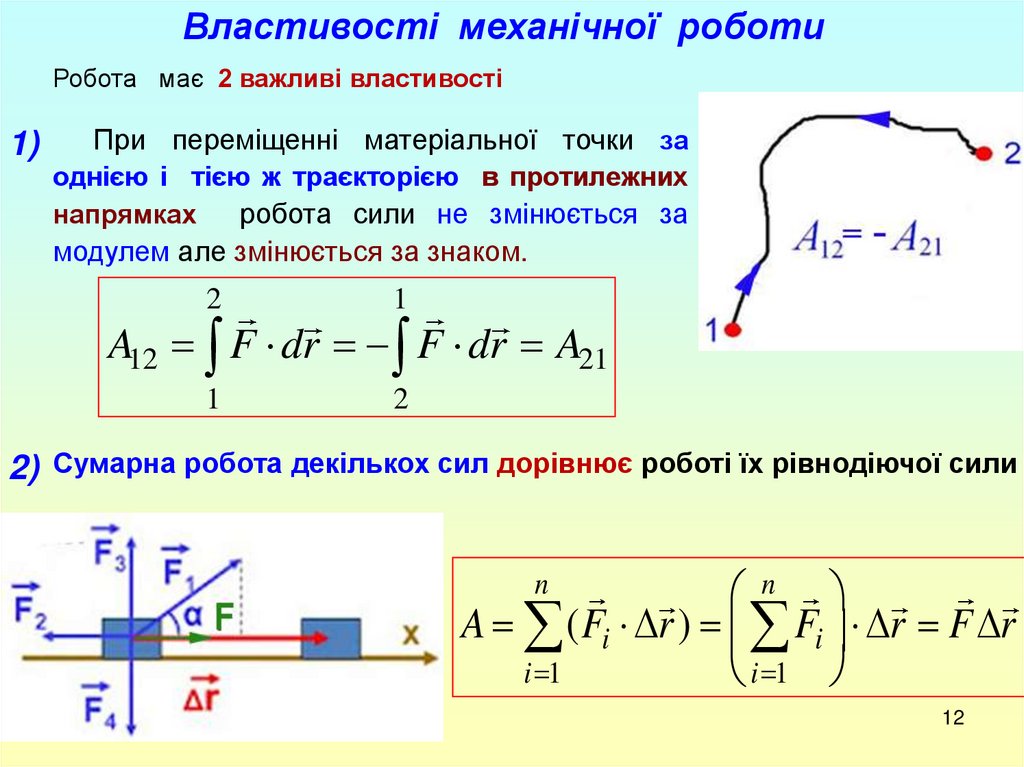
Властивості механічної роботиРобота має 2 важливі властивості
1)
При переміщенні матеріальної точки за
однією і тією ж траєкторією в протилежних
напрямках
робота сили не змінюється за
модулем але змінюється за знаком.
2
1
1
2
A12 F dr F dr A21
2) Сумарна робота декількох сил дорівнює роботі їх рівнодіючої сили
n
A ( Fi r ) Fi r F r
i 1
i 1
n
12
13.
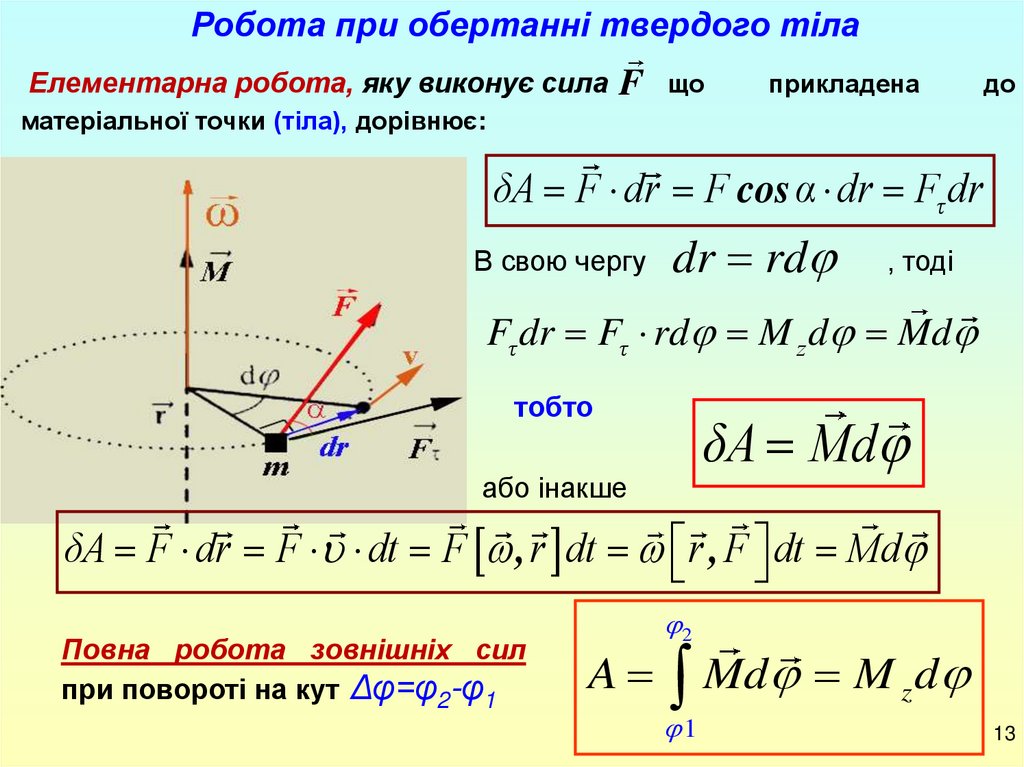
Робота при обертанні твердого тілаЕлементарна робота, яку виконує сила F що
прикладена
до
матеріальної точки (тіла), дорівнює:
δA F dr F cos α dr Fτ dr
В свою чергу
dr rd
, тоді
Fτ dr Fτ rd M z d Md
тобто
δA Md
або інакше
δA F dr F dt F , r dt r , F dt Md
Повна робота зовнішніх сил
при повороті на кут Δφ=φ2-φ1
2
A Md M z d
1
13
14. Потужність
Щоб охарактеризувати швидкість здійснення роботи, вводять поняттяпотужності.
Потужність − це робота, що виконується за одиницю часу.
Середня потужність
A
Pсер
t
Якщо потужність з часом змінюється, то інтенсивність виконання роботи
характеризується миттєвою потужністю:
Миттєва потужність
dA
P
dt
14
15.
Миттєва потужність залежить від сили F , яка виконує роботу А:dA
dr
P F F F cos
dt
dt
− кут між векторами
F та
де
− миттєва швидкість в місці
прикладення сили
Тобто миттєва потужність дорівнює скалярному добутку вектора сили
на вектор швидкості, з якою рухається частинка.
Знаючи потужність можна знайти роботу, яку здійснює сила за
проміжок часу t:
2
t
t
1
0
0
A12 F dr F dt Pdr
Одиниця потужності у системі СІ називається Ват (Вт)
1 Ват дорівнює потужності, за якої виконується робота в 1 Дж за одну секунду.
15
16.
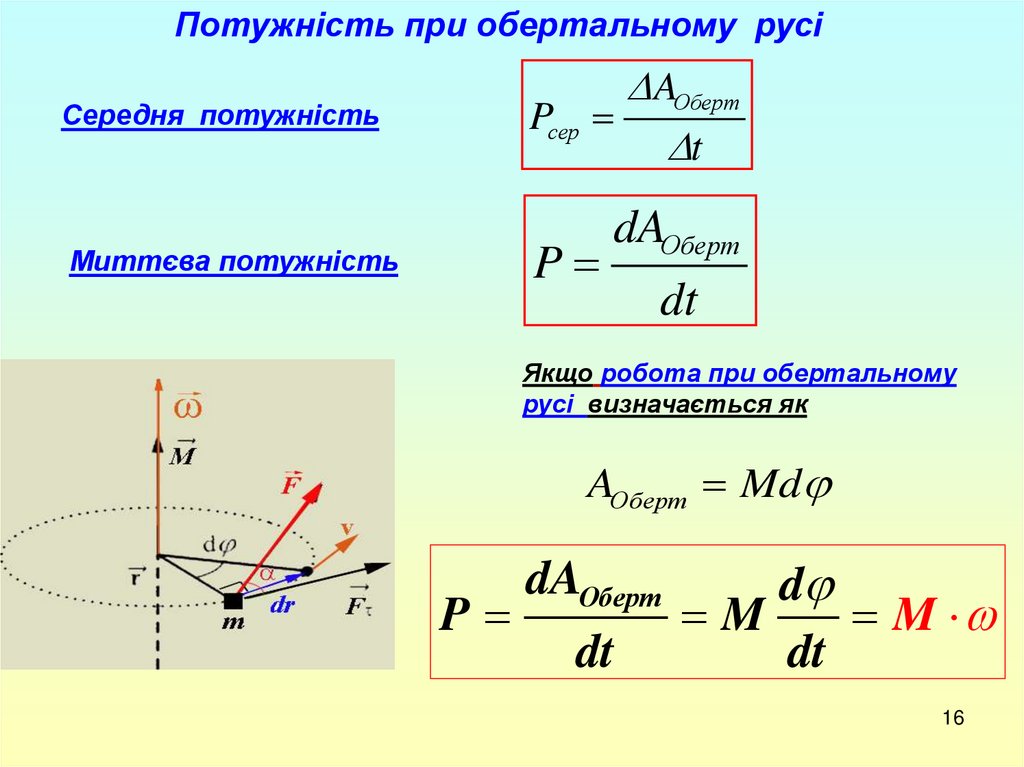
Потужність при обертальному русіAОберт
Pсер
t
Середня потужність
P
Миттєва потужність
dAОберт
dt
Якщо робота при обертальному
русі визначається як
AОберт Md
то
P
dAОберт
dt
d
M
M
dt
16
17.
ЕнергіяУ механіці розглядаються два види енергії − кінетична Wk
потенціальна
Wп .
та
Кінетична енергія
Кінетична енергія тіла або системи тіл - енергія, якою володіє
тіло внаслідок свого руху.
При поступальному русі кінетична енергія визначається як
m 2
Wk
2
де
m− маса матеріальної точки,
v− її швидкість.
Зв’язок кінетичної енергії з імпульсом
Оскількі імпульс дорівнює
p m , то
2
p
Wk
2m
17
18.
Зв'язок кінетичної енергії і роботипри поступальному русі
Нехай тіло масою m поступально рухається під дією деякої сили або
d
результуючої декількох сил F m
dt
на деякому відрізку 1-2 траекторії S
Тоді робота А, яку здійснює сила на цьому відрізку дорівнює
d
dS
m 2
A F dS m dS m d m d
Wk
dt
dt
2
1
1
1
0
2
2
2
v
Висновок: робота сили витрачається на змінення кінетичної енергії
тіла
A Wk
• Якщо А > 0, то енергія тіла зростає, тобто сили (або тіла), які вчиняють
роботу над тілом, віддають йому енергію.
• Якщо А < 0, то енергія тіла зменшується, тобто, тіло віддає енергію
18
оточуючим тілам, здійснюючи над ними роботу.
19.
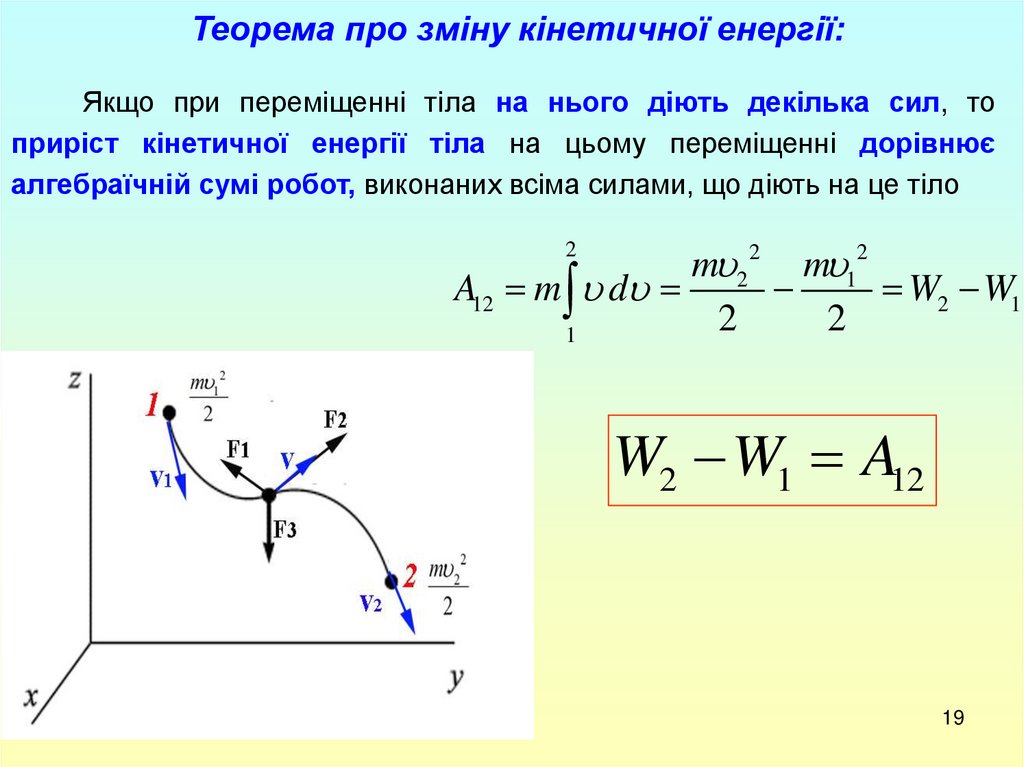
Теорема про зміну кінетичної енергії:Якщо при переміщенні тіла на нього діють декілька сил, то
приріст кінетичної енергії тіла на цьому переміщенні дорівнює
алгебраїчній сумі робот, виконаних всіма силами, що діють на це тіло
m 2 2 m 12
A12 m d
W2 W1
2
2
1
2
W2 W1 A12
19
20.
Властивості кинетичної енергії1. Кінетична енергія завжди позитивна
2. Неоднакова в різних системах відліку.
3. Є функцією стану системи (залежить від швидкості)
4. Кінетична енергія системи матеріальних точок дорівнює
сумі кінетичних енергій
усіх матеріальних точок цієї
системи
mi i
Wk Wkі
i 1
i 1 2
n
n
2
20
21.
Кінетична енергія при обертальному русіЯкщо розглядати тверде тіло як систему
mi , то
матеріальних точок з масами
кінетична енергія елементарної маси
дорівнює
2
mi i
Wkі
2
Враховуючи те, що кінетична енергія
величина адитивна , а також те, що i ri
то для усього тіла кінетична енергія буде визначатися як
mi i
Wk Wkі
i 1
i 1 2
i 1
n
n
Де
n
2
n
mi 2 ri2
2
2
m
R
i i J - момент інерції твердого тіла, тобто
i 1
J 2
2
J
Wk
2
2
22.
Кінетична енергія складного рухуЯкщо тіло рухається таким чином, що його можна уявити як
накладання поступального та обертального,
тобто
коли тіло
обертається навколо осі, що проходить через центр інерції, а сама вісь
разом із тілом рухається поступально, то кінетична енергія тіла дорівнює:
mVC2
J c 2
Wк
2
2
mVC2
2
J c 2
2
Кінетична енергія поступального
руху зі швидкістю його центра мас VC
Кінетична
енергія
обертального руху з кутовой
швидкістю
навколо
осі
обертання
Jc
Момент інерції тіла відносно осі
обертання, що проходить через
центр мас С
23.
Потенціальні та непотенціальні силові поля.Консервативні сили.
Силові поля
При виконанні роботи по переміщенню взаємодія між віддаленими
одне від одного тілами реалізується через силові поля, які утворюються
цими тілами.
Силовим полем називається область простору, в кожній
точці якої на поміщене в неї тіло діє однозначна і визначена
сила, яка може виконувати роботу по переміщенню цього тіла.
Приклади:
- Електростатичне поле
- Гравітаційне поле (поле сил тяжіння)
Існують сили, які не утворюють силових полів,
наприклад сили тертя
24.
Однорідне силове полеОднорідне силове поле – фізичне поле, в якому сили, що діють на
тіло однакові по модулю і за напрямком в усіх точках поля
Стаціонарне силове поле
Стаціонарне силове поле – фізичне поле, в кожній точці якого
сила не залежить від часу
Величина сили в такому полі залежить тільки від положення частинки
24
25.
Потенціальні та непотенціальні силові поля.Робота, яку виконують сили поля при переміщені тіла з точки 1 в
точку 2, в загальному випадку залежить від шляху.
Але серед стаціонарних силових полів є такі, в яких робота не
залежить від шляху, а залежить лише від положення цих точок.
Такі поля називають потенціальними, а сили – консервативними.
Потенціальним
називається
силове
поле,
в
якому
переміщення тіла не залежить від форми траєкторії. ( A12 a A12b ).
робота
Найважливіша
властивість
потенціального
поля
робота
потенціальних сил на будь - якій замкненій
траєкторії дорівнює нулю.
A12 A21 0;
Потенціальними є електростатичне та гравітаційне поля,
25
поле сил пружності, поле ядерних сил.
26.
Непотенціальним називається силове поле, робота в якомузалежить від форми траєкторії руху..
Наприклад,
непотенціальним
електричне поле.
є
вихрове
Сили, що утворюють непотенціальні поля,
називаються
непотенціальними
або
неконсервативними.
До непотенціальних сил відносять сили
тертя, сили опору, а також сили, що залежать
від швидкості частинок, що рухаються і діють
перепендикулярно вектору швидкості. Такими є
Сила Лоренца та сила Коріоліса.
26
27.
Потенціальна енергіяПотенціальна енергія ( Wp) - це частина механічної енергії тіла або
системи тіл, яка залежить від взаємного розташування тіл в просторі та
характеру сил взаємодії між ними.
Потенціальна енергія існує в тільки в потенціальних силових полях
Значення потенціальної енергії в даній точці поля дорівнює роботі
консервативних сил поля по переміщенню тіла з даної точки в точку
простору, де потенціальна енергія прийнята рівною нулю. Як правило, цю
точку вибирають на нескінченності
конс
конс
A
Wp 2
10
p1
20
A
конс
12
A
W
A
конс
10
A
конс
02
де Wр- потенціальна енергія в точці поля
Отже, потенціальна енергія – це енергія,
нерухомого тіла (системи тіл), що обумовлена
27
його взаємодією з іншими тілами.
28.
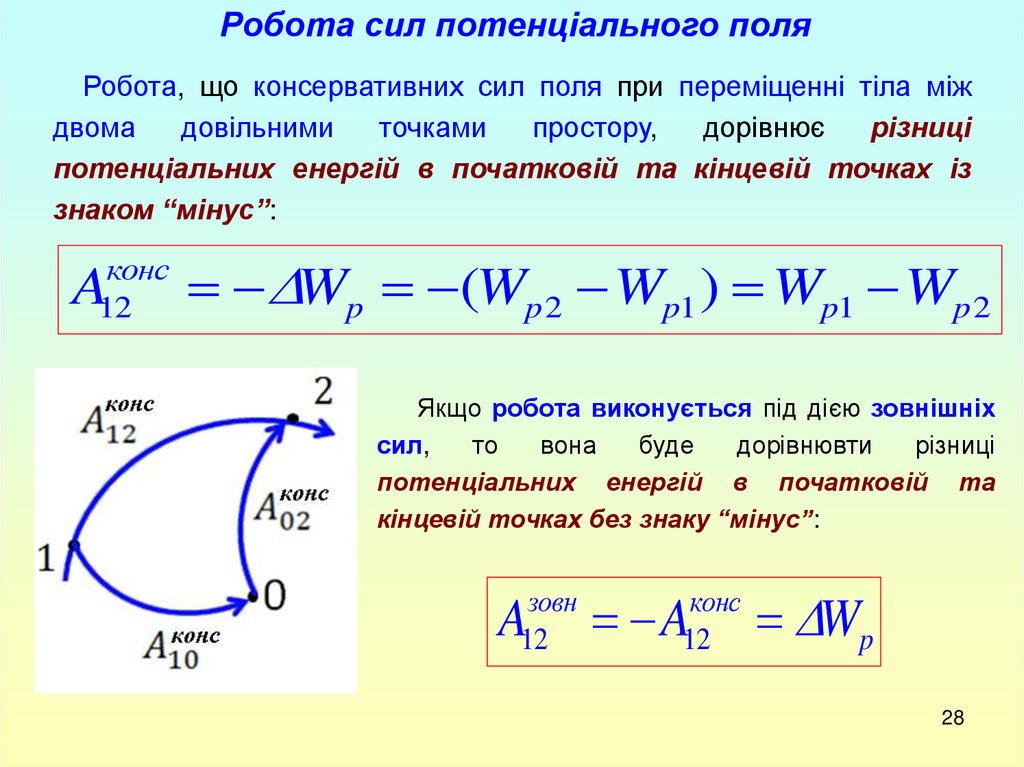
Робота сил потенціального поляРобота, що консервативних сил поля при переміщенні тіла між
двома
довільними
точками
простору,
дорівнює
різниці
потенціальних енергій в початковій та кінцевій точках із
знаком “мінус”:
конс
12
A
Wp (Wp 2 Wp1 ) Wp1 Wp 2
Якщо робота виконується під дією зовнішніх
сил,
то
вона
буде
дорівнювти
різниці
потенціальних енергій в початковій та
кінцевій точках без знаку “мінус”:
зовн
12
A
A
конс
12
Wp
28
29.
Види потенційної енергії в механіціВ механіці розглядають три види потенційної енергії
1. Потенціальна енергія гравітаційної взаємодії двох тіл, з
масами яких m1 та m2:
m1m2
W p ( r ) G
r
де r – відстань між
тілами.
2. Потенціальна енергія сил пружної деформації (наприклад,
деформованої пружини): відстані від поверхні землі
kx 2
Wp ( x )
2
де x − величина деформації,
k – коефіцієнт пружності.
3. Потенціальна енергія тіла в полі сил тяжіння
W p mgh
де h- відстань від поверхні
Землі
29
30.
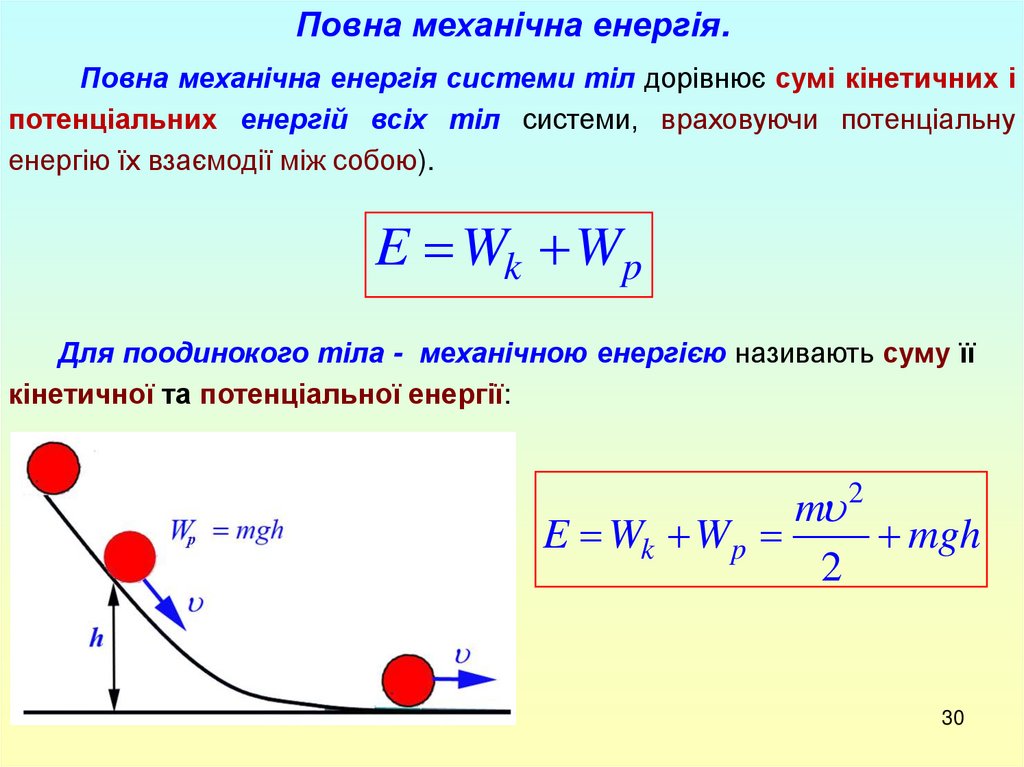
Повна механічна енергія.Повна механічна енергія системи тіл дорівнює сумі кінетичних і
потенціальних енергій всіх тіл системи, враховуючи потенціальну
енергію їх взаємодії між собою).
E Wk Wp
Для поодинокого тіла - механічною енергією називають суму її
кінетичної та потенціальної енергії:
m 2
E Wk Wp
mgh
2
30
31. Закон збереження повної механічної енергії системи
Якщо в системі діють лише потенціальні сили, то повнамеханічна енергія системи матеріальних точок не змінюється.
E Wk W p const
Приклад: Куля кинута під деяким кутом до горизонту знаходиться під дією
сил тяжіння. Її повна механічна енергія на протязі руху від точки А до точки
В буде незмінною.
m 02
m 2
mgh0
mgh
2
2
31
32.
Теорема про повну механічну енергіюЗагальний закон збереження енергії
Якщо в системі діють непотенціальні сили (сили тертя), то зміна
повної енергії системи дорівнює роботі не потенціальних сил:
непот
E2 Е1 A12
В такому випадку повна механічна енергія системи не
зберігається. Але замість механічної енергії завжди виникає
еквівалентна кількість енергії іншого виду, тобто:
« Енергія не виникає з нічого і не зникає в нікуди, а
може лише перетворюватись з однієї форми на іншу».
ЗАГАЛЬНИЙ ЗАКОН ЗБЕРЕЖЕННЯ ЕНЕРГІЇ
33.
Зіткнення двох тілЯскравим прикладом застосування законів збереження є процес
зіткнення двох тіл.
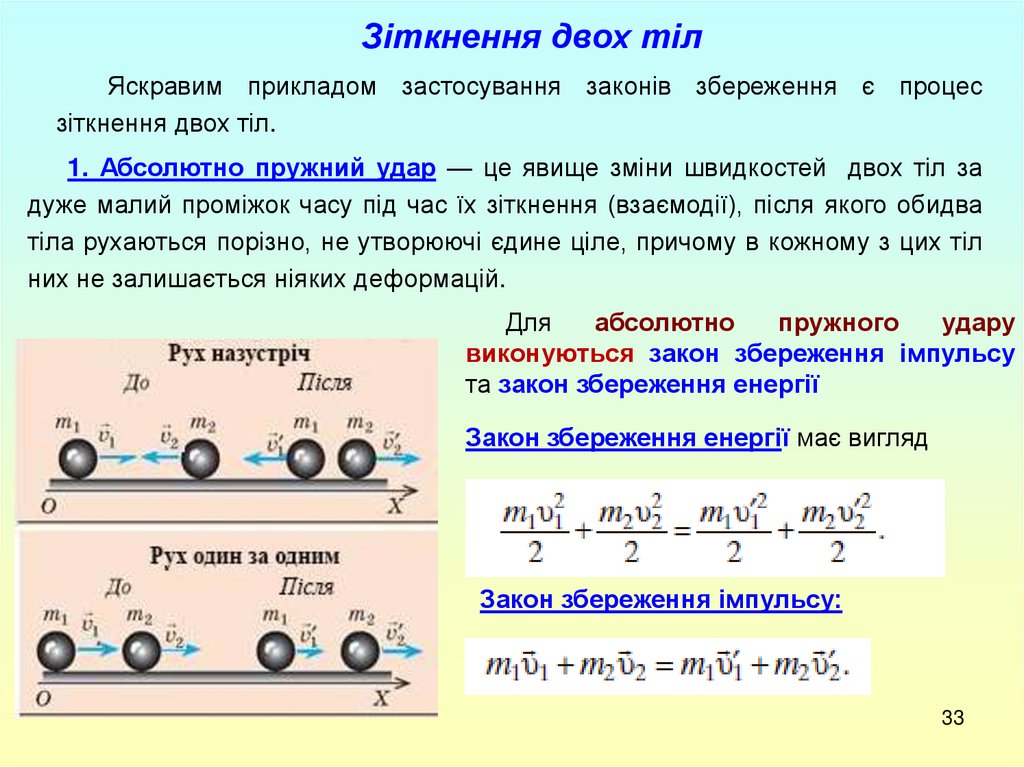
1. Абсолютно пружний удар — це явище зміни швидкостей двох тіл за
дуже малий проміжок часу під час їх зіткнення (взаємодії), після якого обидва
тіла рухаються порізно, не утворюючі єдине ціле, причому в кожному з цих тіл
них не залишається ніяких деформацій.
Для
абсолютно
пружного
удару
виконуються закон збереження імпульсу
та закон збереження енергії
Закон збереження енергії має вигляд
Закон збереження імпульсу:
33
34.
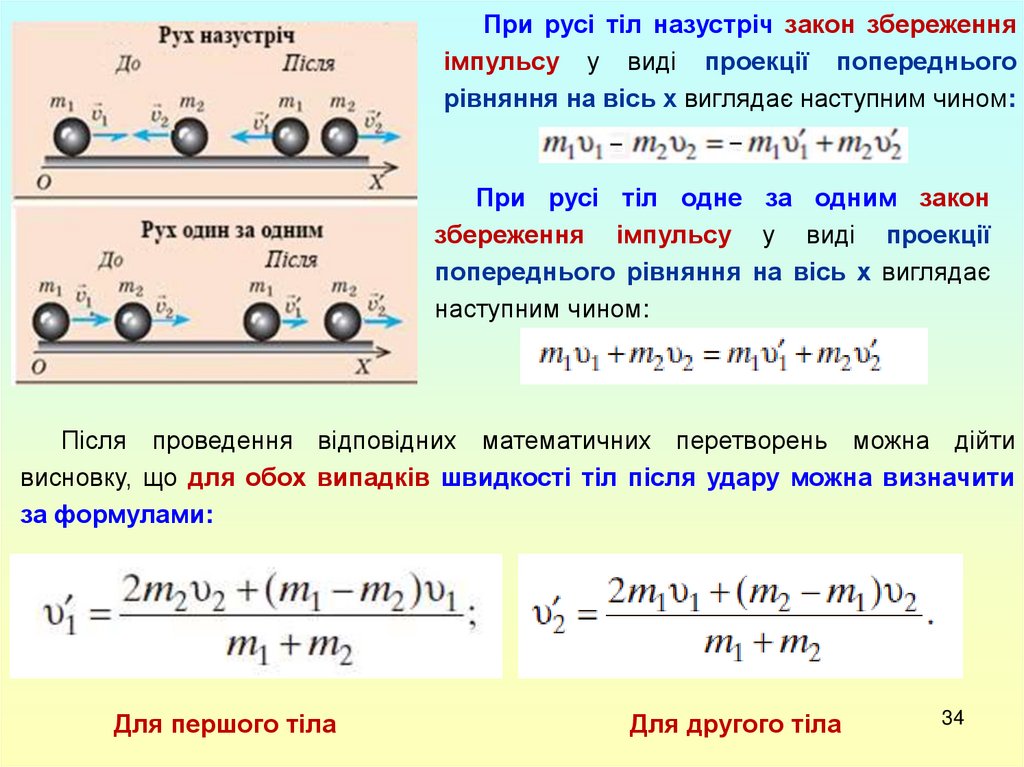
При русі тіл назустріч закон збереженняімпульсу у виді проекції попереднього
рівняння на вісь х виглядає наступним чином:
При русі тіл одне за одним закон
збереження імпульсу у виді проекції
попереднього рівняння на вісь х виглядає
наступним чином:
Після проведення відповідних математичних перетворень можна дійти
висновку, що для обох випадків швидкості тіл після удару можна визначити
за формулами:
Для першого тіла
Для другого тіла
34
35.
Окремі випадки руху тіл при абсолютно пружному ударіа) m1 = m2;
υ′2 = υ1; υ′1 = υ2 - тіла однакової маси обмінюються швидкостями;
б) m1 = m2; υ2 = 0; υ′1 = 0; υ′2 = υ1 - друге тіло до удару було нерухомим,
після удару перше тіло зупинилось, а друге тіло рухатиметься у томуж напрямку ,
що і перше тіло до удару;
в)
m1>> m2; υ′1 = 2υ2 - υ1; υ′2 υ2 - друге тіло практично не змінює свою
швидкість
г) m1>> m2; υ′2 = 0; υ′1 -υ1 - перше тіло відбивається від нерухомого другого
масивного тіла і рухається зворотному напрямку з початковою швидкістю.
35
36.
Абсолютно пружний удар тіл рівних мас, але з різниминапрямками та модулями швидкостей
Абсолютно пружний удар двох тіл різних мас
36
37.
2. Абсолютно непружний удар - зіткнення двох тіл, у результаті якоговони об’єднуються і рухаються далі як єдине ціле.
При цьому частина механічної енергії при
деформації переходить у внутрішню енергію.
Закон збереження механічної енергії не
виконується.
Зберігається сумарна енергія — механічна і
внутрішня.
Закон збереження імпульсу при взаємодії
двох тіл, що створюють замкнену систему,
при непружньому ударі має вигляд:
в скалярному виді:
де u — швидкість системи після зіткнення
37
38.
Швидкість системи з двох тіл після зіткнення при непружному ударі :( )
Зміна кінетичної енергії тіл до і після удару:
Зменшення механічної енергії системи двох тіл супроводжується
зростанням внутрішньої енергії цієї системи Wвн:
З урахуванням ( ) одержимо, що зміна внутрішньої енергії при
непружному ударі
38
39.
Контрольні запитання та завдання для самоперевірки1. Яка фізична величина називається механічною роботою? Запишіть роботу сили
на малому та нескінченно малому переміщенні.
2. Запишіть вирази для роботи при різних формах задання руху.
3. Яка фізична величина називається потужністю? Середньою потужністю?
Миттєвою потужністю?
4. Як миттєва потужність пов’язана із діючою силою і швидкістю руху?
5. Чи може сила, завдяки якій тіло набуває доцентрового прискорення, виконувати
роботу?
6. Чи залежить робота, що здійснюється над тілом, від вибору системи відліку?
7. Який зв’язок кінетичної енергії системи з роботою діючих на систему сил?
8. Чи може кінетична енергія бути від’ємною? А зміна кінетичної енергії? Поясніть.
9.Чим характеризуються консервативні і неконсервативні сили? Чим вони
відрізняються?
10. Від чого залежить потенціальна енергія механічної системи?
11. Який зв’язок між потенціальною силою, що діє на матеріальну точку,
і потенціальною енергією цієї точки?
12. Як потенціальна енергія пов’язана з роботою консервативних сил?
39
13. Як розрахувати роботу сили пружності?
40.
14. Визначте роботу сили гравітаційної взаємодії двох точкових тіл.15. Розрахуйте роботу сили тяжіння. Як вона пов’язана з потенціальною
енергією?
16. Яка система називається замкненою?
17. Сформулюйте закон збереження механічної енергії в загальному випадку, а
також при дії тільки консервативних сил.
18. Що таке абсолютно пружний, абсолютно непружний і частково пружний
удари?
19. Які закони збереження виконуються в кожному з цих випадків?
40
41.
Kiнець лекції41




























 physics
physics








