Similar presentations:
Параллельность плоскостей
1. Параллельность плоскостей
2. Цели урока
Образовательная:Познакомиться с
расположением плоскостей в
пространстве;
признаком параллельности
плоскостей;
свойствами параллельных
плоскостей.
Воспитательная:
Воспитание
взаимопомощи.
внимания,
Развивающая: Организовать свою
деятельность, направляя её на
3.
« Среди равных умовпри одинаковости
прочих условий
превосходит тот, кто
знает геометрию. »
Б. Паскаль
4. Взаимное расположение двух прямых в пространстве
1. Прямые пересекаются, т.е. имеютодну общую точку
2. Прямые параллельны, т.е. лежат в
одной плоскости
3. Прямые скрещиваются, т.е. не лежат
в одной плоскости
5. Взаимное расположение прямой и плоскости в пространстве
1. Прямая и плоскость параллельны2. Прямая пересекает плоскость
3 . Прямая принадлежит плоскости
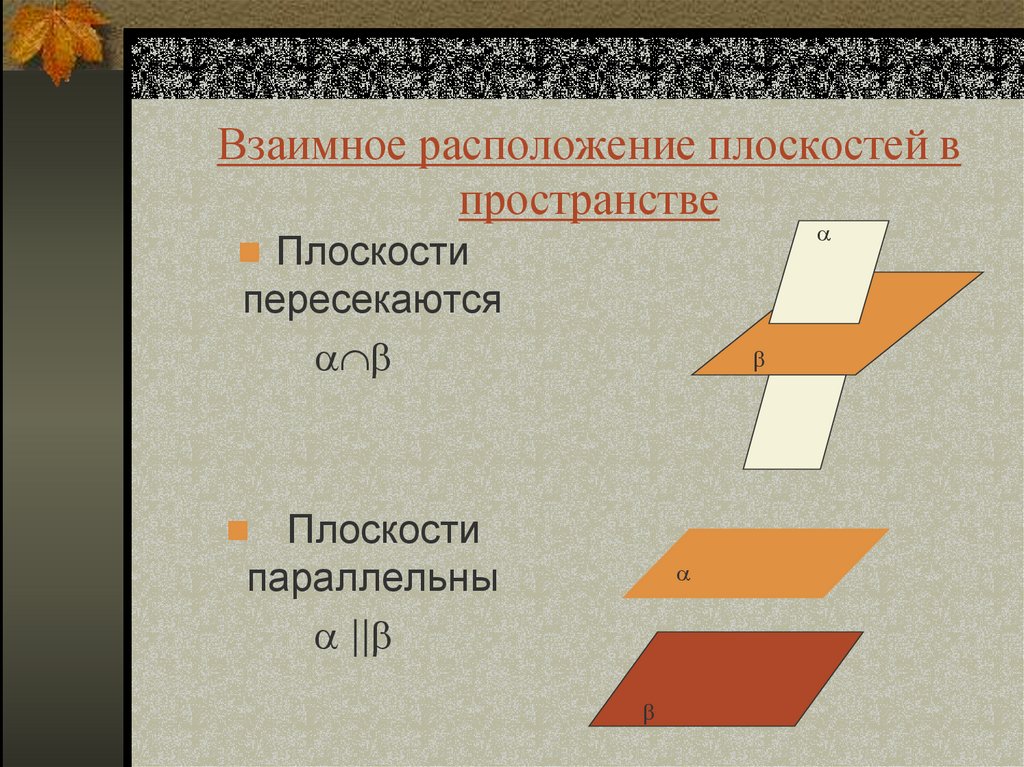
6. Взаимное расположение плоскостей в пространстве
Плоскостипересекаются
Плоскости
параллельны
||
7.
Важнейшее требованиематематической наукитребование точного определения
понятий.
Евклид
8. определение
Две плоскости называютсяпараллельными, если они не
пересекаются.
9. Признак параллельности плоскостей Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся
прямым другой плоскости, тоэти плоскости параллельны.
о
b
a
о1
b1
a1
10. Задача № 51 ( еще один признак параллельности плоскостей)
Дано: m n = К,m , n ,
n|| , m|| .
Доказать: ||
К
m
n
с
Доказательство : Допустим, что и не параллельны. Тогда
они пересекаются по прямой с. Так как n|| , m|| , то n||с, m||с.
Получаем, что через точку К проходят две прямые ,
параллельные прямой с , что невозможно по теореме
параллельных прямых. Получили противоречие.
Значит, ||
11.
Часто случается, что доказательствоот противного более уместно и
сокращает рассуждение.
Гаусс К.
12. Свойства параллельных плоскостей
1. Если две параллельныеплоскости пересекаются, то
линии их пересечения
параллельны.
2. Отрезки параллельных
прямых, заключенных
между параллельными
плоскостями , равны.
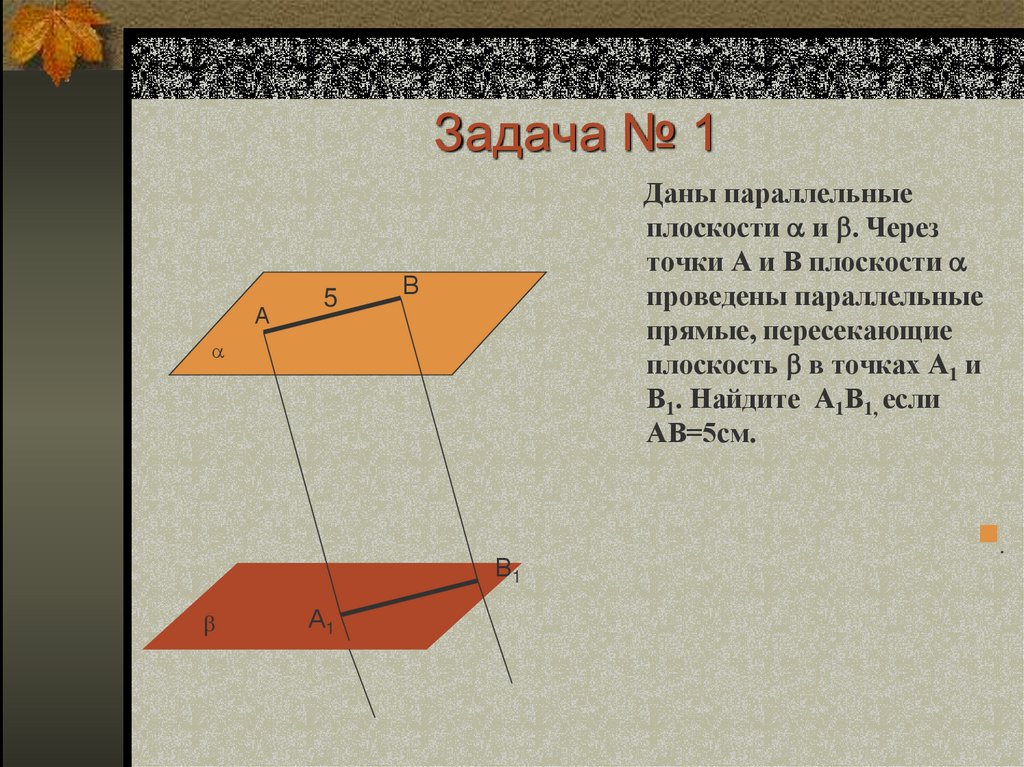
13. Задача № 1
А5
Даны параллельные
плоскости и . Через
точки А и В плоскости
проведены параллельные
прямые, пересекающие
плоскость в точках А1 и
В1. Найдите А1В1, если
АВ=5см.
В
В1
А1
.
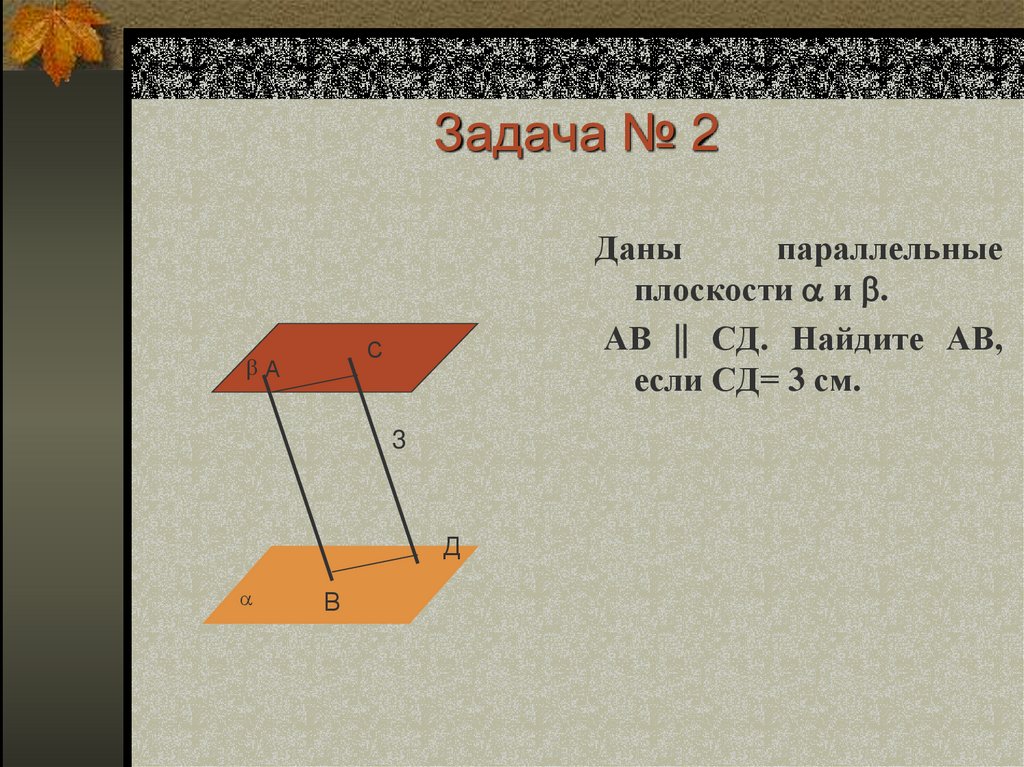
14. Задача № 2
Даныпараллельные
плоскости и .
АВ || СД. Найдите АВ,
если СД= 3 см.
С
А
3
Д
В
15. Задача № 3
Через точку О, расположеннуюмежду параллельными
плоскостями и ,
проведены две прямые,
которые пересекают
плоскости в точках А и А1, В
и В1
1)
Как расположены прямые
АВ и А1В1 ?
(Ответ поясните.)
2)
Найдите длину отрезка А1В1,
если АВ = 18 см, АО : ОАг = 3:5.
16. Задача № 4
Через точки В1 и В2 стороныАВ равностороннего
треугольника ABC
проведены плоскости и ,
параллельные прямой ВС.
1) На какие фигуры делится
этот треугольник
плоскостями и ?
2) Вычислите периметры
фигур АВ1С1 и АВ2С2, если
АС = 18 см и AB1 :АВ = 1:3.
17.
Математику нельзя изучать,наблюдая, как это делает
сосед!
К.Маркс













 mathematics
mathematics








