Алгоритм метода северо-западного угла

1.

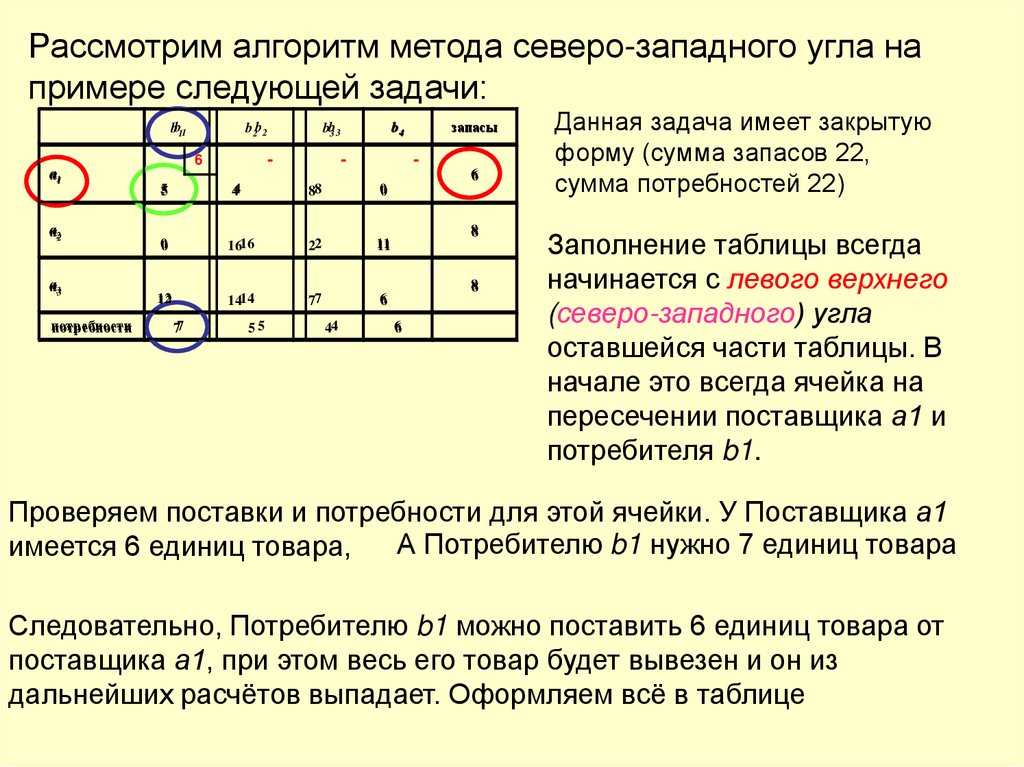
Рассмотрим алгоритм метода северо-западного угла на
примере следующей задачи:
bb11
а1
а2
а3
потребности
b2b2
bb3 3
-
6
-
-
5
44
88
0
0
1616
22
11
12
1414
77
6
77
55
44
запасы
b4
6
8
8
6
Данная задача имеет закрытую
форму (сумма запасов 22,
сумма потребностей 22)
Заполнение таблицы всегда
начинается с левого верхнего
(северо-западного) угла
оставшейся части таблицы. В
начале это всегда ячейка на
пересечении поставщика а1 и
потребителя b1.
Проверяем поставки и потребности для этой ячейки. У Поставщика а1
А Потребителю b1 нужно 7 единиц товара
имеется 6 единиц товара,
Следовательно, Потребителю b1 можно поставить 6 единиц товара от
поставщика а1, при этом весь его товар будет вывезен и он из
дальнейших расчётов выпадает. Оформляем всё в таблице

2.

b11
b22
66
а11
55
а22
а33
потребности
b33
-
4
8
-
16
2
11
14
7
6
8
12
12
7
6
0
1
00
запасы
b44
8
5
4
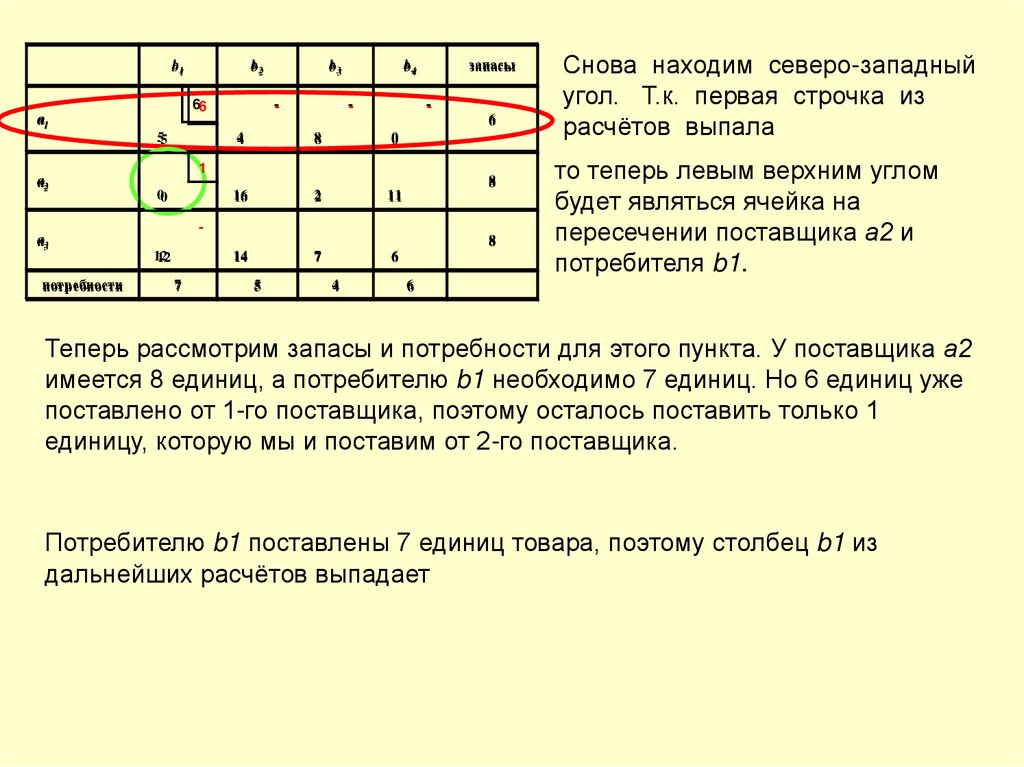
Снова находим северо-западный
угол. Т.к. первая строчка из
расчётов выпала
то теперь левым верхним углом
будет являться ячейка на
пересечении поставщика а2 и
потребителя b1.
6
Теперь рассмотрим запасы и потребности для этого пункта. У поставщика а2
имеется 8 единиц, а потребителю b1 необходимо 7 единиц. Но 6 единиц уже
поставлено от 1-го поставщика, поэтому осталось поставить только 1
единицу, которую мы и поставим от 2-го поставщика.
Потребителю b1 поставлены 7 единиц товара, поэтому столбец b1 из
дальнейших расчётов выпадает

3.

bb1 1
bb22
66
а1а1
а3а3
потребности
потребности
--
запасы
bb44
--
-6
55
а2а2
bb33
44
11
88
00
22
11
11
77
66
5
8
00
16
16
--
8
12
12
77
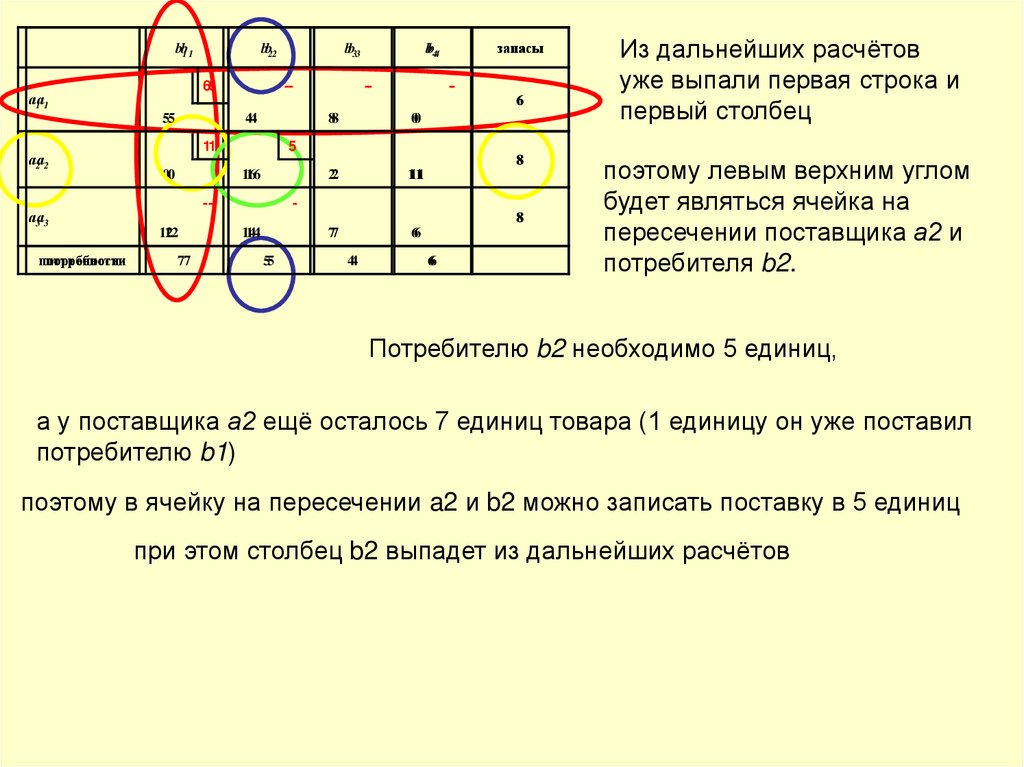
Из дальнейших расчётов
уже выпали первая строка и
первый столбец
14
14
55
44
66
поэтому левым верхним углом
будет являться ячейка на
пересечении поставщика а2 и
потребителя b2.
Потребителю b2 необходимо 5 единиц,
а у поставщика а2 ещё осталось 7 единиц товара (1 единицу он уже поставил
потребителю b1)
поэтому в ячейку на пересечении a2 и b2 можно записать поставку в 5 единиц
при этом столбец b2 выпадет из дальнейших расчётов

4.

bb1
1
а11
а2
а3
потребности
bb2
2
6
5
bb3
3
-
4
0
-
2
5
6
2
11
7
6
8
8
4
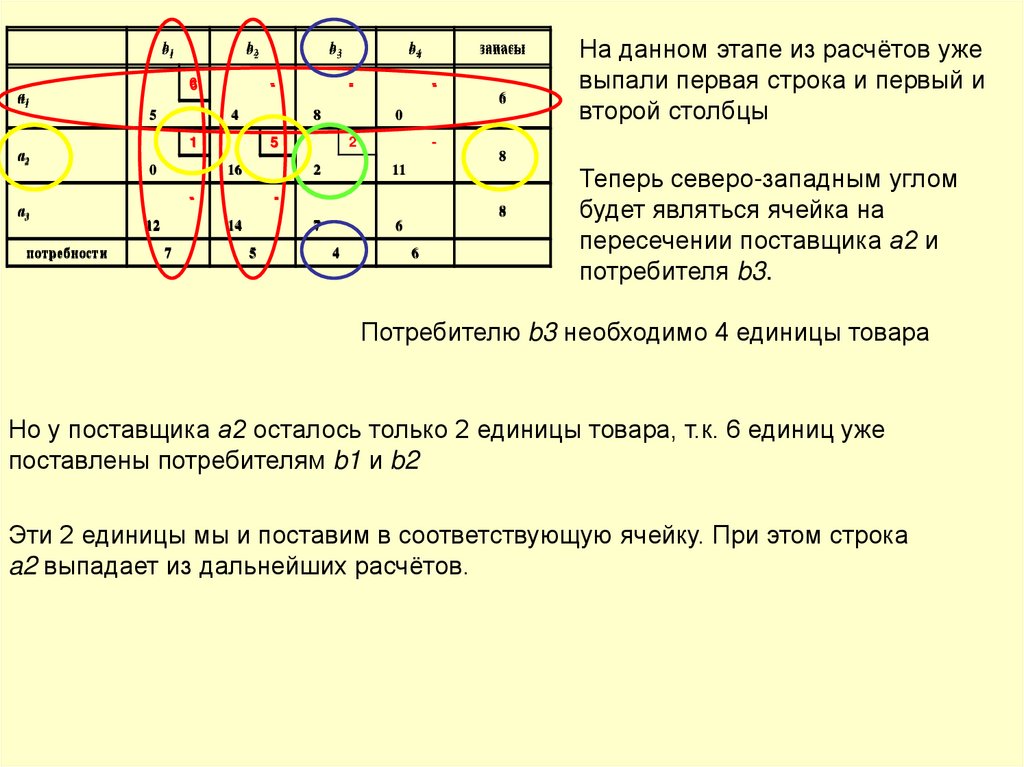
На данном этапе из расчётов уже
выпали первая строка и первый и
второй столбцы
-
14
7
0
5
16
12
8
1
запасы
запасы
bb4
4
6
Теперь северо-западным углом
будет являться ячейка на
пересечении поставщика а2 и
потребителя b3.
Потребителю b3 необходимо 4 единицы товара
Но у поставщика а2 осталось только 2 единицы товара, т.к. 6 единиц уже
поставлены потребителям b1 и b2
Эти 2 единицы мы и поставим в соответствующую ячейку. При этом строка
a2 выпадает из дальнейших расчётов.

5.

bb11
bb22
66
аа11
55
-44
00
12
12
потребности
потребности
77
2
88
2
77
5
66
11
11
-14
14
00
22
--
аа33
-
55
16
16
запасы
запасы
bb44
88
11
аа22
b33
88
66
44
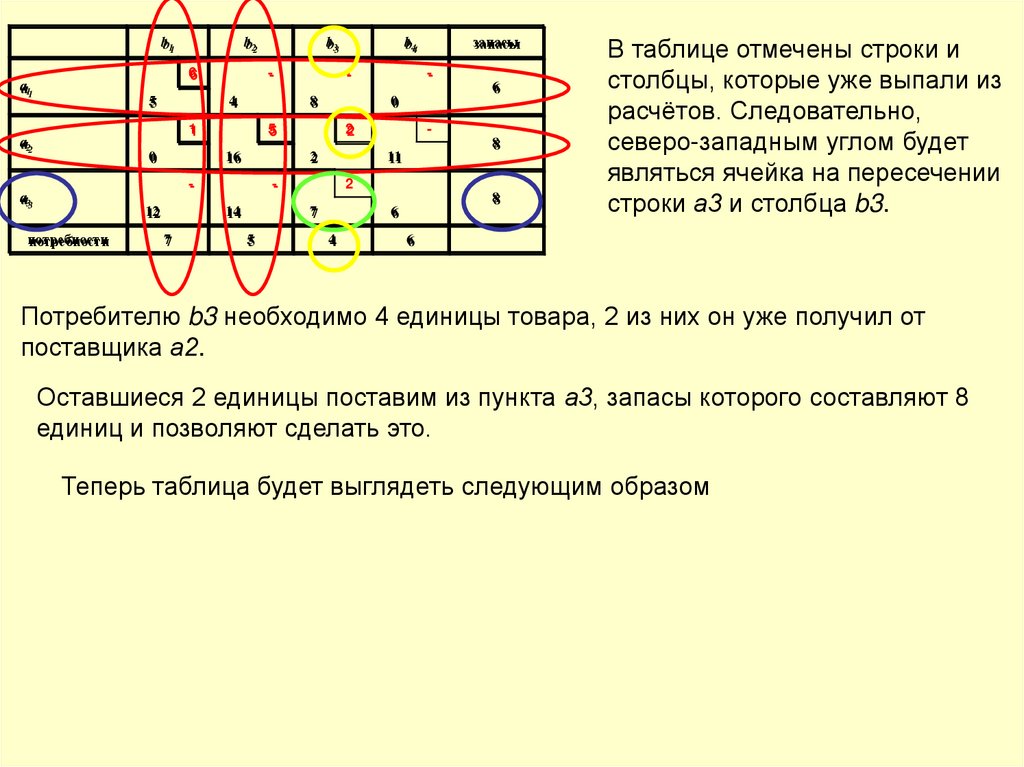
В таблице отмечены строки и
столбцы, которые уже выпали из
расчётов. Следовательно,
северо-западным углом будет
являться ячейка на пересечении
строки а3 и столбца b3.
66
Потребителю b3 необходимо 4 единицы товара, 2 из них он уже получил от
поставщика а2.
Оставшиеся 2 единицы поставим из пункта а3, запасы которого составляют 8
единиц и позволяют сделать это.
Теперь таблица будет выглядеть следующим образом

6.

b
b11
66
а1 а1
а2
b
b2 2
b3
- -
b3
-
запасы
запасы
b4
b4
-
-
-
6
5
44
8 8
1
1
а2
0
0
а3
-
потребности
12 7
потребности
7
2
5
16
16
12
а3
5
0
-
2
11
2
7
74
5
8
2
-
145
8
11
14
0
2
2
6
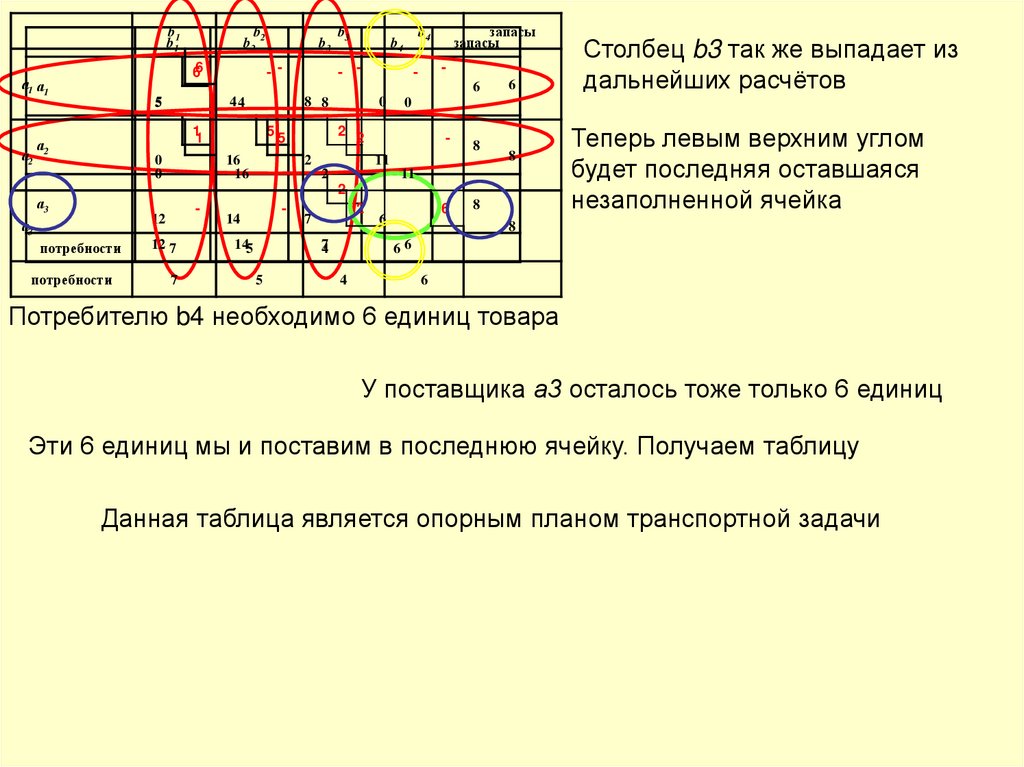
Столбец b3 так же выпадает из
дальнейших расчётов
6
6
8
Теперь левым верхним углом
будет последняя оставшаяся
незаполненной ячейка
8
66
4
6
Потребителю b4 необходимо 6 единиц товара
У поставщика а3 осталось тоже только 6 единиц
Эти 6 единиц мы и поставим в последнюю ячейку. Получаем таблицу
Данная таблица является опорным планом транспортной задачи

7.

b1
b2
6
а1
b3
-
запасы
b4
-
6
5
4
8
1
а2
0
5
2
8
0
16
2
-
а3
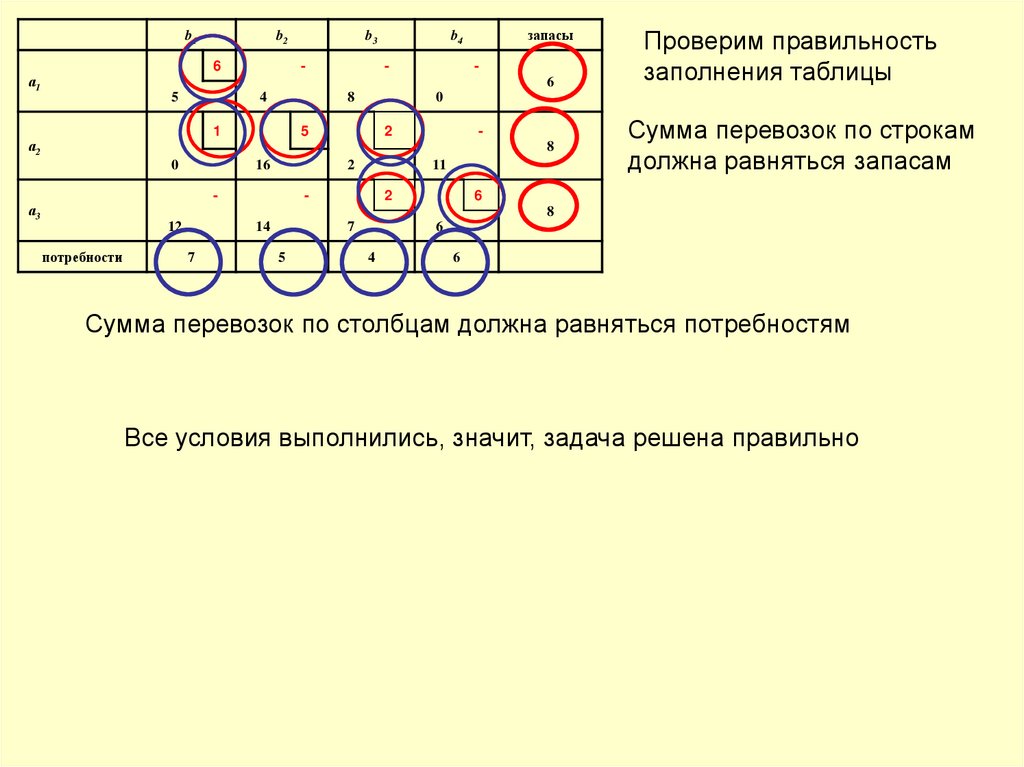
Проверим правильность
заполнения таблицы
11
-
2
Сумма перевозок по строкам
должна равняться запасам
6
8
12
потребности
14
7
7
5
6
4
6
Сумма перевозок по столбцам должна равняться потребностям
Все условия выполнились, значит, задача решена правильно

8.

b1
b2
6
b3
-
запасы
b4
-
-
а1
6
5
4
8
1
0
5
2
-
а2
8
0
16
2
-
а3
11
-
2
6
8
12
потребности
14
7
7
5
6
4
6
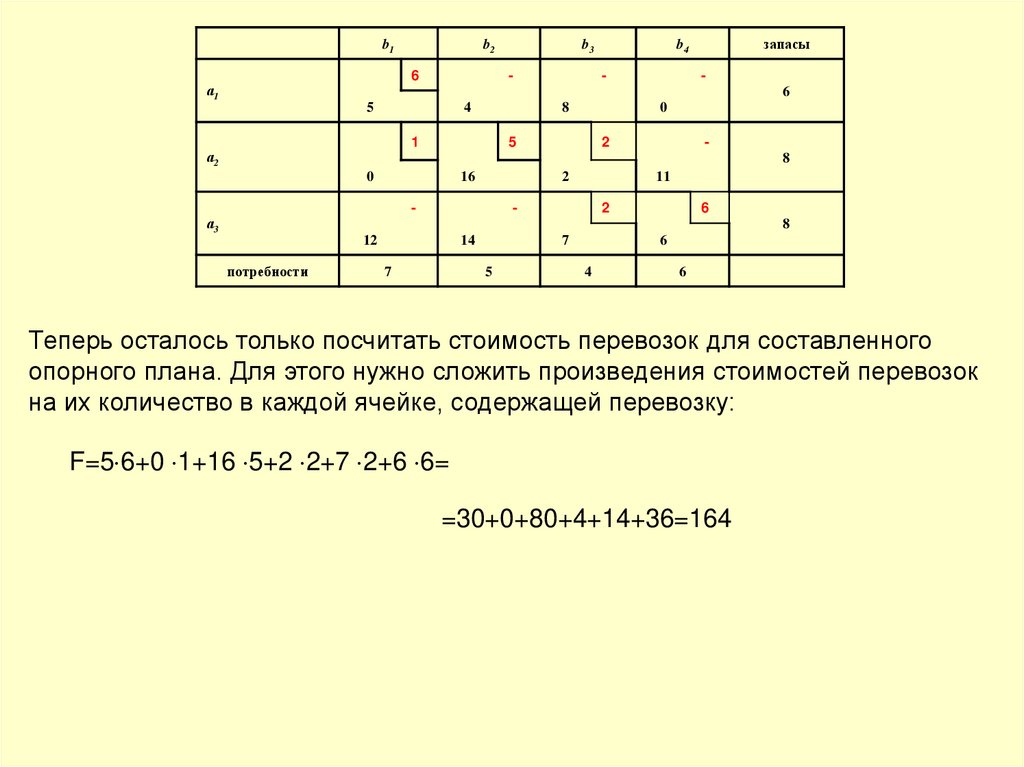
Теперь осталось только посчитать стоимость перевозок для составленного
опорного плана. Для этого нужно сложить произведения стоимостей перевозок
на их количество в каждой ячейке, содержащей перевозку:
F=5 6+0 1+16 5+2 2+7 2+6 6=
=30+0+80+4+14+36=164