Компьютерная графика. Лекция 2. Геометрические преобразования

1.

КОМПЬЮТЕРНАЯ
ГРАФИКА
Лекция 2
«Геометрические
преобразования»
Лектор, зав. кафедрой, к.т.н.
Степанченко Илья Викторович
Камышин 2009
Кафедра
автоматизированных
систем обработки
информации и
управления

2.

2.1. АФФИННЫЕ
ПРЕОБРАЗОВАНИЯ НА
ПЛОСКОСТИ
Декартовы координаты (Cartesian coordinates) – это
точка, называемая началом координат, и базисные
векторы, называемые осями, исходящими из начала
координат. Точка в этой системе задается координатами
(их число зависит от размерности системы, в данном
разделе их будет две).
Декартовы прямоугольные координаты (orthogonal
coordinates) – декартовы координаты, у которых угол
между осями (базисными векторами) прямой.
Преобразование декартовых координат. Отвечает на
вопрос как найти пару координат (x*, y*) в новой системе
координат по заданным (x, y) в старой системе
координат и по заданному положению (начало новой
системы координат и положение осей).

3.

2.1. АФФИННЫЕ
ПРЕОБРАЗОВАНИЯ НА
ПЛОСКОСТИ
Переход от одной координатной системы к другой на
плоскости описывается следующими уравнениями
x x y ,
*
y x y .
*
Коэффициенты , , , зависят от наклона
новых базисных векторов (О1х*) и (О1y*) по
отношению к (Ох) и (Оy).
Коэффициенты , зависят от положения
начала координат.
(1)

4.

2.1. АФФИННЫЕ
ПРЕОБРАЗОВАНИЯ НА
ПЛОСКОСТИ
Преобразование (1) можно выполнить при любых
, , , , , . Однако обратное преобразование от
(x*, y*) к (x, y) можно выполнить, только если
базисные вектора (О1х*) и (О1y*) не параллельны.
det
0
(2)

5.

2.1. АФФИННЫЕ
ПРЕОБРАЗОВАНИЯ НА
ПЛОСКОСТИ
Преобразование (1) двойственно.
y
y
x
O
x
O

6.

2.1. АФФИННЫЕ
ПРЕОБРАЗОВАНИЯ НА
ПЛОСКОСТИ
Аффинным преобразованием (affine
transformation) называют линейное и
взаимооднозначное отображение функции R в
функцию Р, ставящее в соответствие точки из
плоскости R точкам на плоскости Р. Аффинное
преобразование удовлетворяет уравнениям (1) и
(2).
Существует 4 частных случая аффинных
преобразований.

7.

2.1. АФФИННЫЕ
ПРЕОБРАЗОВАНИЯ НА
ПЛОСКОСТИ
1. Поворот (rotation) точки на угол относительно
начала координат.
Задача: по заданным координатам (х, у) и углу
найти (х*, у*), где – сценарий, а (х, у) – данные.
у
* *
у
у
*
М (х , у )
*
r
М(х, у)
r
х
*
х
х

8.

2.1. АФФИННЫЕ
ПРЕОБРАЗОВАНИЯ НА
ПЛОСКОСТИ
x* r cos( ) r cos cos r sin sin x cos y sin ,
y* r sin( ) r cos sin r sin cos x sin y cos .
x * x cos y sin ,
y* x sin y cos .
x
*
y
*
x y R ( ).
данны е
сц ен ар и й
cos
R( )
sin
sin
.
cos

9.

2.1. АФФИННЫЕ
ПРЕОБРАЗОВАНИЯ НА
ПЛОСКОСТИ
2. Растяжение/сжатие (dilatation/squeeze) вдоль
координатных осей.
Задача: по заданным координатам (х, у) и
параметрам , найти (х*, у*), где , – сценарий,
а (х, у) – данные.
y
M* (x*, y*)
M (x, y)
О
х

10.

2.1. АФФИННЫЕ
ПРЕОБРАЗОВАНИЯ НА
ПЛОСКОСТИ
x* = x; > 0;
y* = y; > 0.
Зависимость изображения от параметров , :
Если >0, а =1 изменится вид по OX;
Если =1, а >0 изменится вид по OY;
Если <1, и/или <1 – изображение сожмется;
Если >1, и/или >1 – изображение растянется.
x *
y * x
y
0
. D( , )
0
0
0
.

11.

2.1. АФФИННЫЕ
ПРЕОБРАЗОВАНИЯ НА
ПЛОСКОСТИ
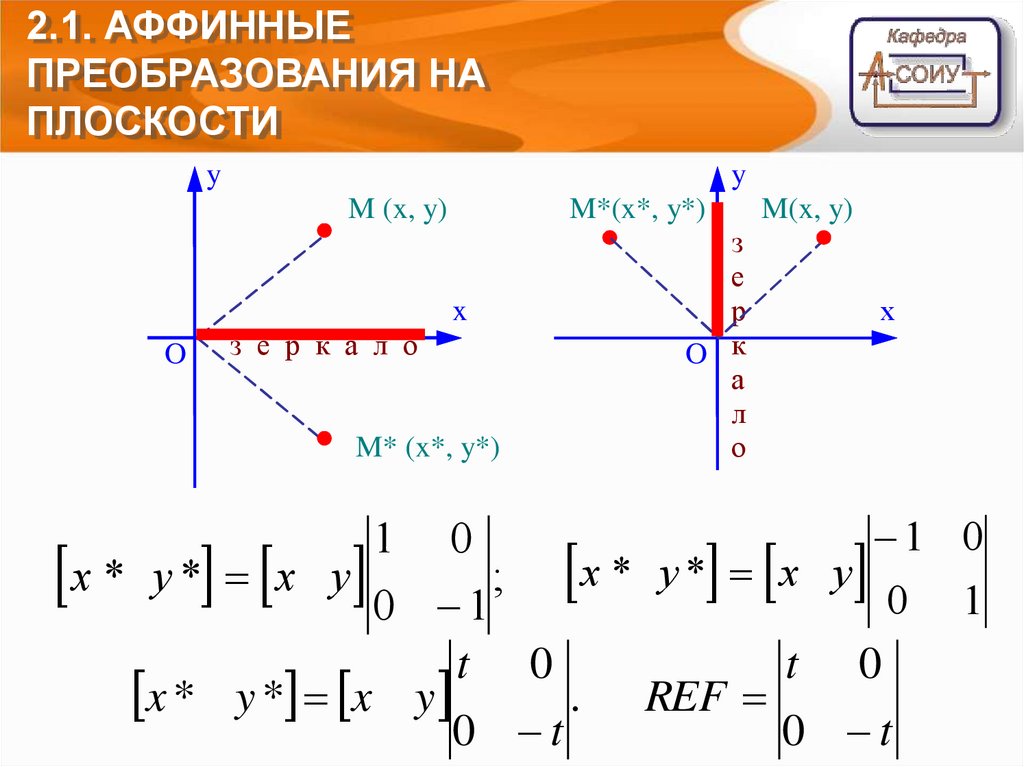
3. Зеркальное отражение (reflection)
относительно оси абсцисс или ординат.
Задача: по заданным координатам (х, у) и
параметру t (ось отражения) найти (х*, у*), где t –
сценарий, а (х, у) – данные.
y
y
M (x, y)
M*(x*, y*)
x
O
з е р к а л о
M* (x*, y*)
з
е
р
O к
а
л
о
M(x, y)
х

12.

2.1. АФФИННЫЕ
ПРЕОБРАЗОВАНИЯ НА
ПЛОСКОСТИ
y
y
M (x, y)
M*(x*, y*)
x
O
з е р к а л о
M* (x*, y*)
з
е
р
O к
а
л
о
M(x, y)
х
1 0
1 0
x * y* x y
; x * y * x y
0 1
0 1
t 0
t 0
x * y * x y
. REF
0 t
0 t

13.

2.1. АФФИННЫЕ
ПРЕОБРАЗОВАНИЯ НА
ПЛОСКОСТИ
4. Перемещение (transition, transposition) точки
по вектору ( , .
Задача: по заданным координатам (х, у) и
параметрам , найти (х*, у*), где , – сценарий,
а (х, у) – данные.
y
M*(x*, y*)
M(x,y)
O
x

14.

2.1. АФФИННЫЕ
ПРЕОБРАЗОВАНИЯ НА
ПЛОСКОСТИ
x* = x + ,
y* = y + .
Попытаемся создать матрицу:
[x* y*] = [x y] T( , ).
x * y * 1 x
1
y 1 0
0
1
1 0 0
0
0 , T ( , ) 0 1 0 .
1
1

15.

2.2. ОДНОРОДНЫЕ КООРДИНАТЫ
В основе метода однородных координат лежит
представление о том, что каждая точка в N-мерном
пространстве может рассматриваться как проекция
точки из (N+1)-мерного пространства.
Однородными координатами (uniform
coordinates) называют масштабное изображение
реальных координат и сам масштаб.
x1
x,
x3
x2
y,
x3
Пример. Если у нас имеется точка (0.3; 0.1), а нам необходимы целые
координаты, то х3 можно выбрать равным 10, т.е. однородные
координаты (3; 1; 10).

16.

2.2. ОДНОРОДНЫЕ КООРДИНАТЫ
а) поворот на угол относительно начала
cos sin 0
координат:
R( ) sin cos 0 .
0
0
1
б) растяжение (сжатие) с параметрами , :
0
D( , ) 0
0
0
0
0.
1

17.

2.2. ОДНОРОДНЫЕ КООРДИНАТЫ
в) Отражение (относительно оси OX и оси OY):
1 0 0
1 0 0
REF(OY ) 0 1 0 .
REF(OX ) 0 1 0 ,
0 0 1
0 0 1
г) Перемещение с параметрами , :
1
T ( , ) 0
0
1
0
0.
1

18.

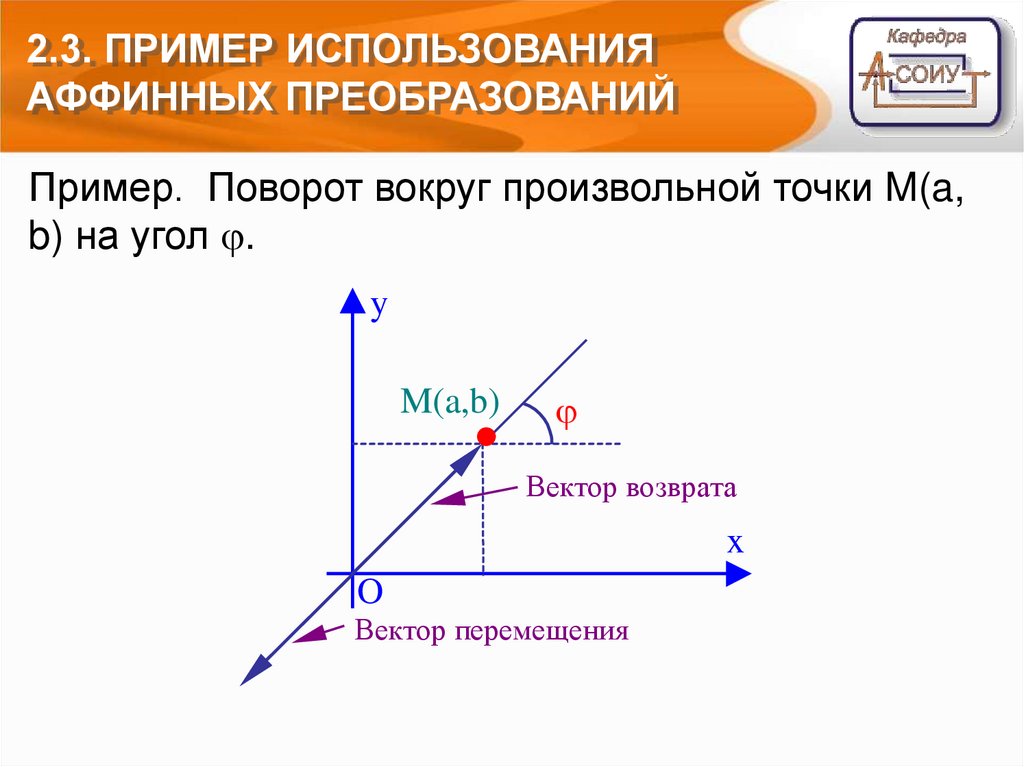
2.3. ПРИМЕР ИСПОЛЬЗОВАНИЯ
АФФИННЫХ ПРЕОБРАЗОВАНИЙ
Пример. Поворот вокруг произвольной точки M(a,
b) на угол .
y
M(a,b)
Вектор возврата
x
O
Вектор перемещения

19.

2.3. ПРИМЕР ИСПОЛЬЗОВАНИЯ
АФФИННЫХ ПРЕОБРАЗОВАНИЙ
1. Перенос точки в начало координат на вектор (а, b) –
таким образом совмещаем центр поворота с точкой:
[x* y* 1] = [x y 1] T(-а, -b).
2. Поворот на относительно начала координат:
[x** y** 1] = [x* y* 1] R( ) = [x y 1] T(-а, -b) R( ).
3. Возврат точки в прежнее положение по вектору (a, b):
[x*** y*** 1] = [x** y** 1] T(а, b).
После подстановки из шага 2:
[x*** y*** 1] = [x y 1] [T(-а, -b) R( ) T(а, b)],
где [x y 1] – данные, [T(-а, -b) R( ) T(а, b)] – сценарий.

20.

2.3. ПРИМЕР ИСПОЛЬЗОВАНИЯ
АФФИННЫХ ПРЕОБРАЗОВАНИЙ
cos
sin
0
sin
cos
0
a cos b sin a a sin b cos b 1