Similar presentations:
Возрастание и убывание функции
1. Возрастание и убывание функции
2.
Изучение нового материалау=х,
r=1
у = х² ,
r=2
у=1/х,
где
r = -1
у =√х,
r=1/2
у = х³ ,
r=3
у = х r , где
r -заданное число
3.
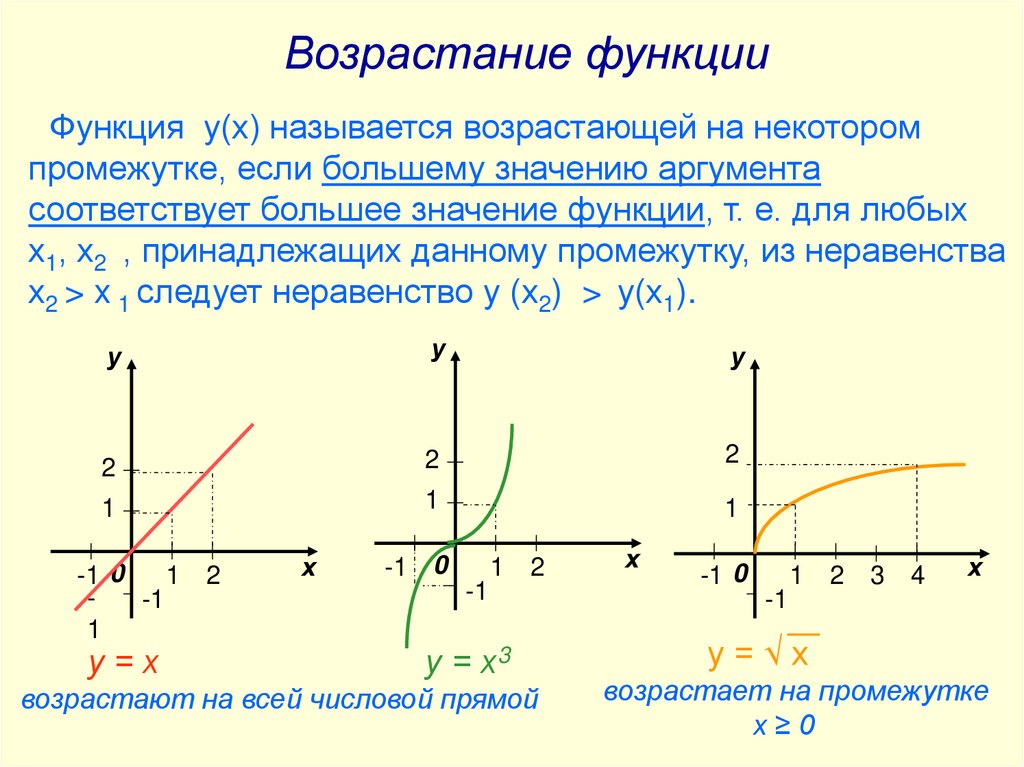
Возрастание функцииФункция у(х) называется возрастающей на некотором
промежутке, если большему значению аргумента
соответствует большее значение функции, т. е. для любых
х1, х2 , принадлежащих данному промежутку, из неравенства
х2 > x 1 следует неравенство у (х2) > у(х1).
у
у
у
2
2
2
1
1
1
-1 0
1
-1
1
у=х
2
х
-1
0
1
2
-1
у = х3
возрастают на всей числовой прямой
х
-1 0
1
2
3
4
х
-1
у=√х
возрастает на промежутке
х≥0
4.
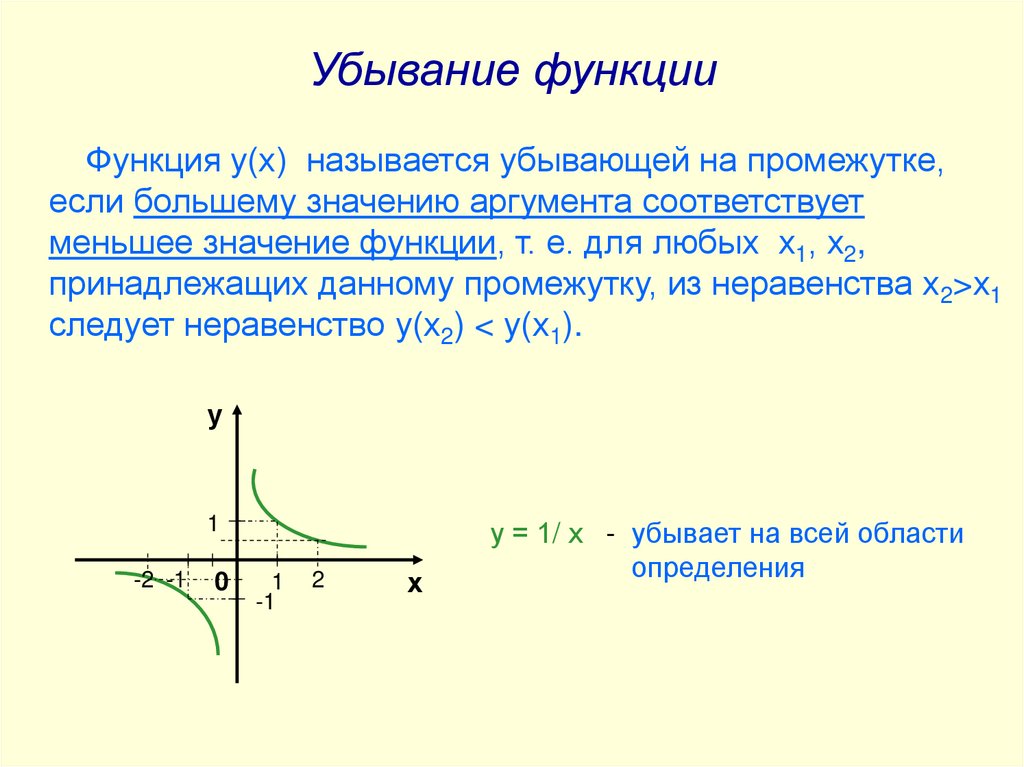
Убывание функцииФункция у(х) называется убывающей на промежутке,
если большему значению аргумента соответствует
меньшее значение функции, т. е. для любых х1, х2,
принадлежащих данному промежутку, из неравенства х2>х1
следует неравенство у(х2) < у(х1).
у
1
-2 -1
0
1
-1
2
х
у = 1/ х - убывает на всей области
определения
5.
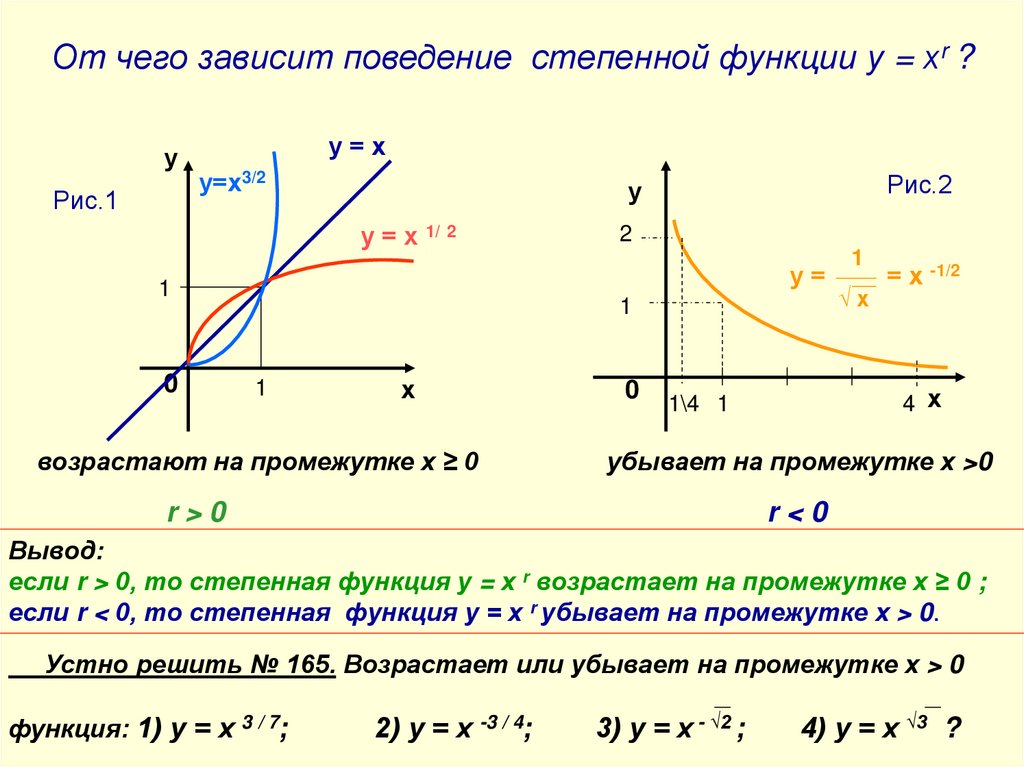
От чего зависит поведение степенной функции у = хr ?у
Рис.1
у=х
у=х3/2
у = х 1/ 2
2
у=
1
0
Рис.2
у
1
1
х
возрастают на промежутке х ≥ 0
0
1
√х
= х -1/2
4 х
1\4 1
убывает на промежутке х >0
r>0
r<0
Вывод:
если r > 0, то степенная функция у = х r возрастает на промежутке х ≥ 0 ;
если r < 0, то степенная функция у = х r убывает на промежутке х > 0.
Устно решить № 165. Возрастает или убывает на промежутке х > 0
функция: 1) у = х 3 / 7;
2) у = х -3 / 4;
3) у = х - √2 ;
4) у = х √3 ?
6.
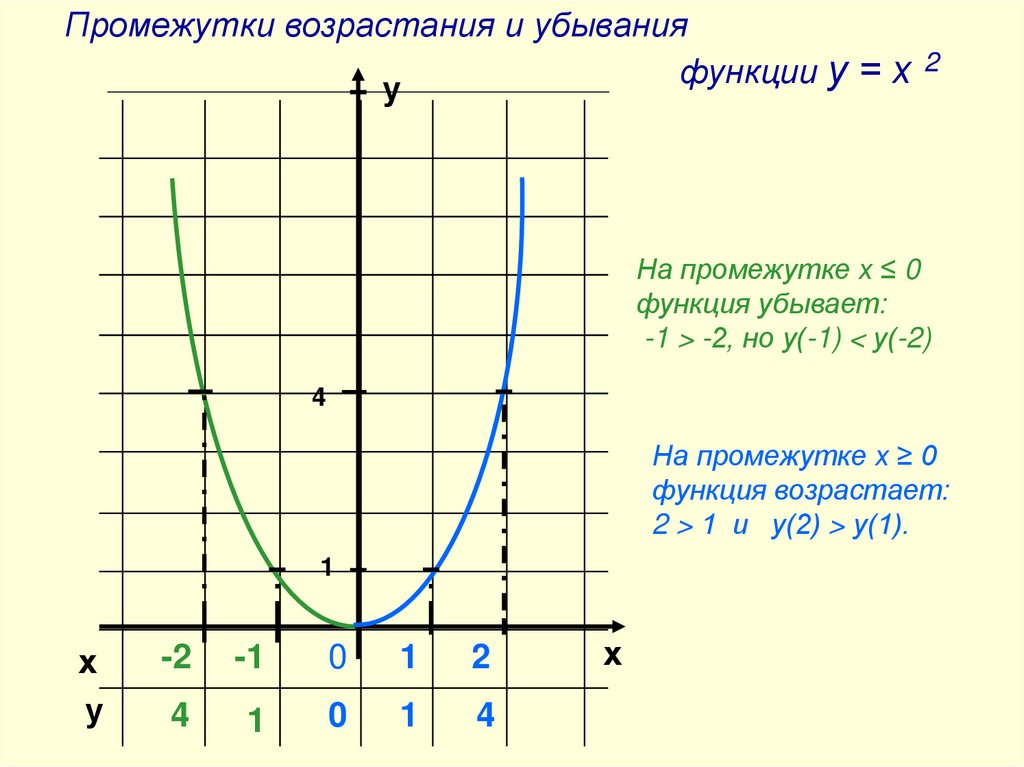
Промежутки возрастания и убывания2
функции
у
=
х
у
На промежутке х ≤ 0
функция убывает:
-1 > -2, но у(-1) < у(-2)
4
На промежутке х ≥ 0
функция возрастает:
2 > 1 и у(2) > у(1).
1
х
у
-2
-1
0
1
2
4
1
0
1
4
х
7.
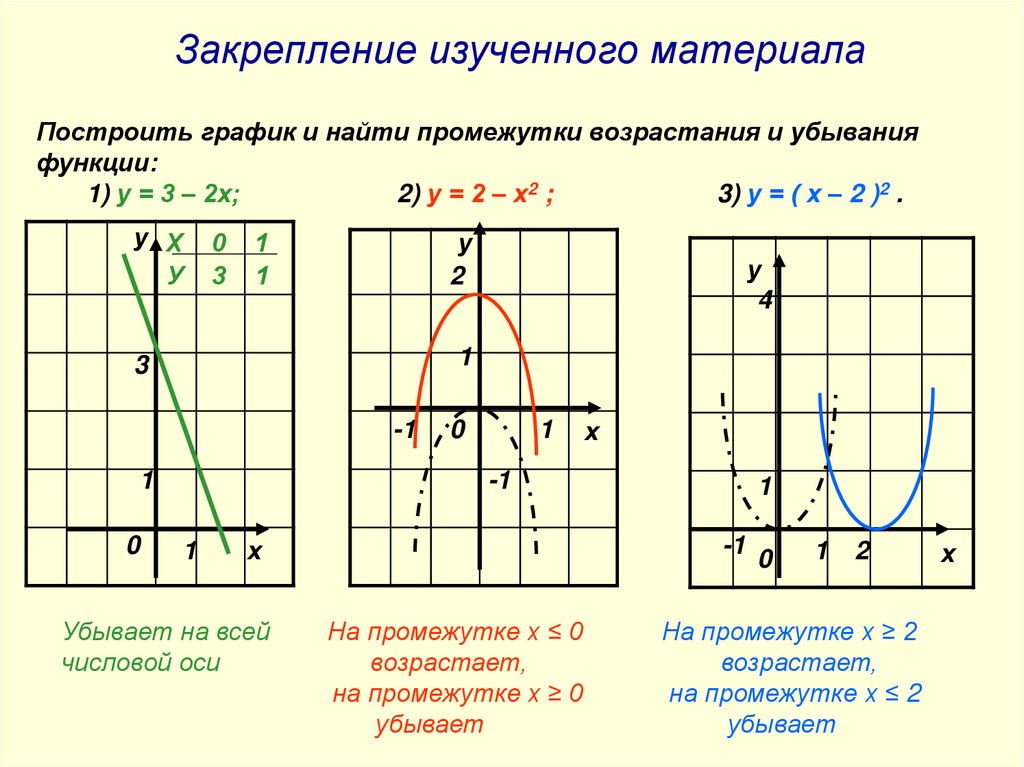
Закрепление изученного материалаПостроить график и найти промежутки возрастания и убывания
функции:
1) у = 3 – 2х;
2) у = 2 – х2 ;
3) у = ( х – 2 )2 .
у Х
У
0
3
1
1
у
2
1
3
-1
1
0
у
4
0
1
х
-1
1
-1
х
Убывает на всей
числовой оси
1
На промежутке х ≤ 0
возрастает,
на промежутке х ≥ 0
убывает
0
1
2
На промежутке х ≥ 2
возрастает,
на промежутке х ≤ 2
убывает
х
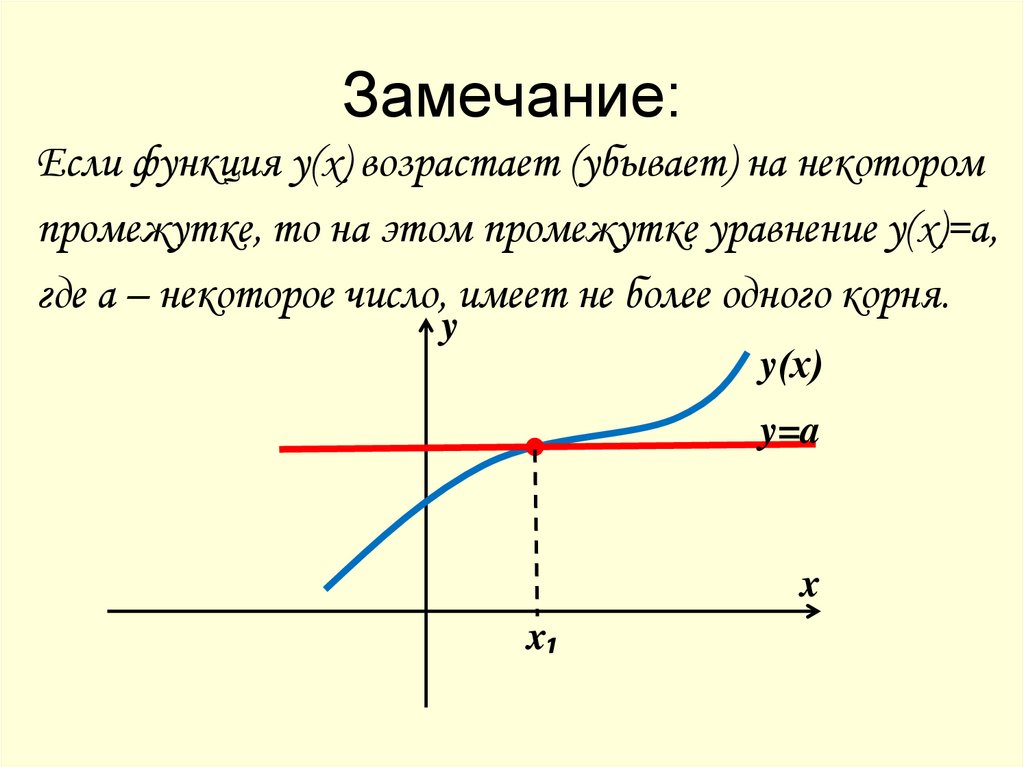
8. Замечание:
Если функция у(х) возрастает (убывает) на некоторомпромежутке, то на этом промежутке уравнение у(х)=а,
где а – некоторое число, имеет не более одного корня.
y
y(х)
y=a
x
x₁
9. Решение уравнений вида хr =a
Функция вида у=хr называется ….степенной
возрастает
При r>0 функция….
убывает
При r<0 функция ….
Значит при х>0 может быть не
….более одного корня
1
r
xr a
1
1
( xr ) r a r
x ra
10.
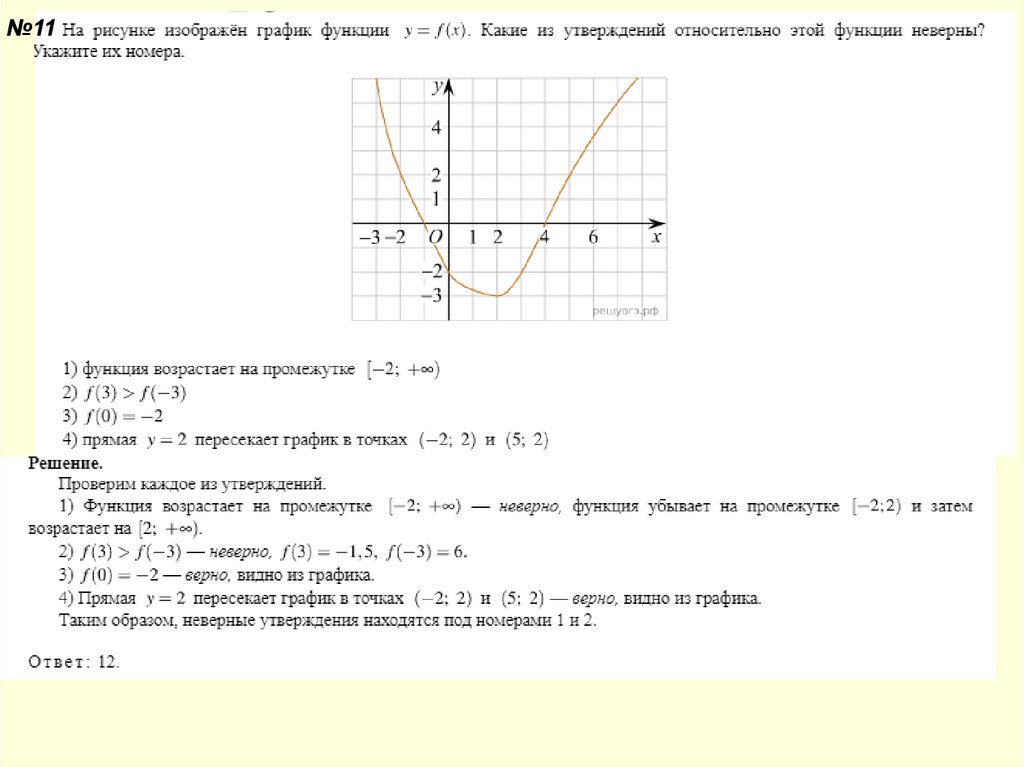
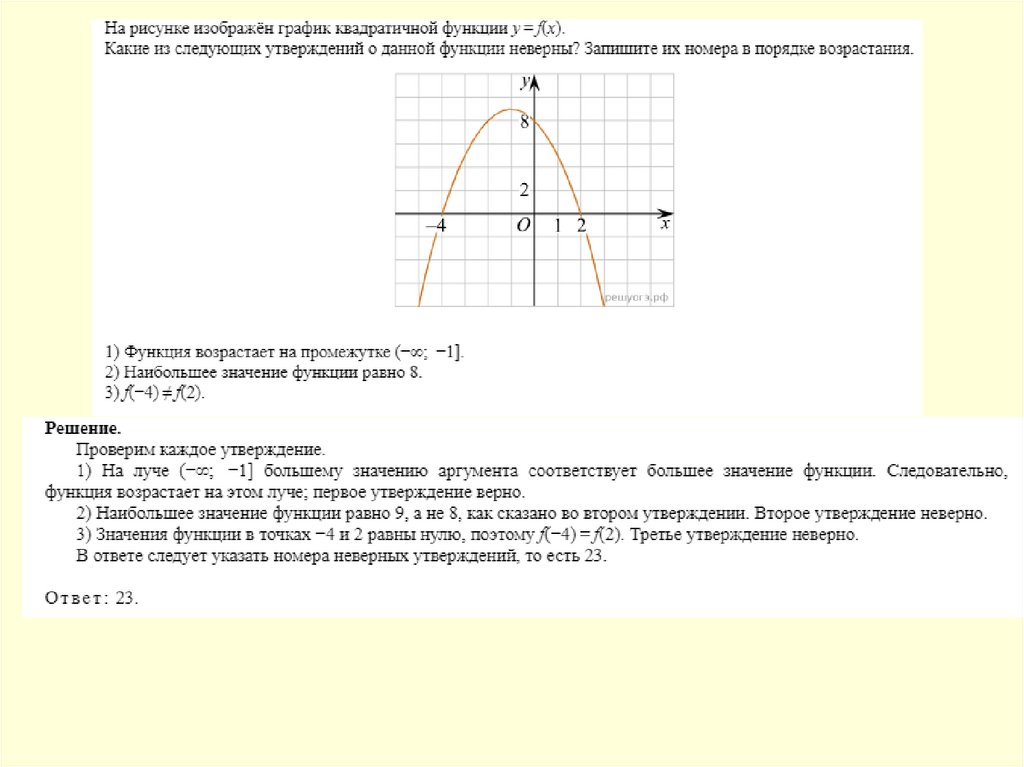
№1111.
12.
13.
14.
Слайд 11.у
Найти
промежутки
возрастания и
убывания
функций:
о
х≥-2-возр.,
х≤-2-убыв.;
д
возр.на всей
числ. оси;
ц
х≤-3-возр.,
х≥-3-убыв.;
л
4
4
3
2
2
3
1
-4
-3
-2
-1
0
6
х≤0-возр.,
х≥0-убыв.;
2
3
х
4
1
-2
-3
на х≥0- возрастает;
на
м убывает
всей числ. оси.
1
-1
5
ы
7
1
2
М о
3
4
5
6
7
л о д ц ы!
П
р
о
в
е
р
ь
с
е
б
я
!
15. Домашнее задание
1. Учебник стр.48-50, §7 изучить2. Посмотреть видеоурок https://clck.ru/YpFR4
3. Выполнить необходимые записи в рабочей тетради
с указанием темы урока
4. Выполнить задание на платформе ЯКласс
https://clck.ru/YpGFV





 mathematics
mathematics








