Прямоугольный треугольник

1. ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК

2. ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК

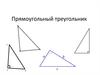
А
Если один из углов треугольника - прямой,
то треугольник называется прямоугольным.
С
Сторона прямоугольного треугольника, лежащая
против прямого угла, называется гипотенузой, а
две другие – катетами.
В

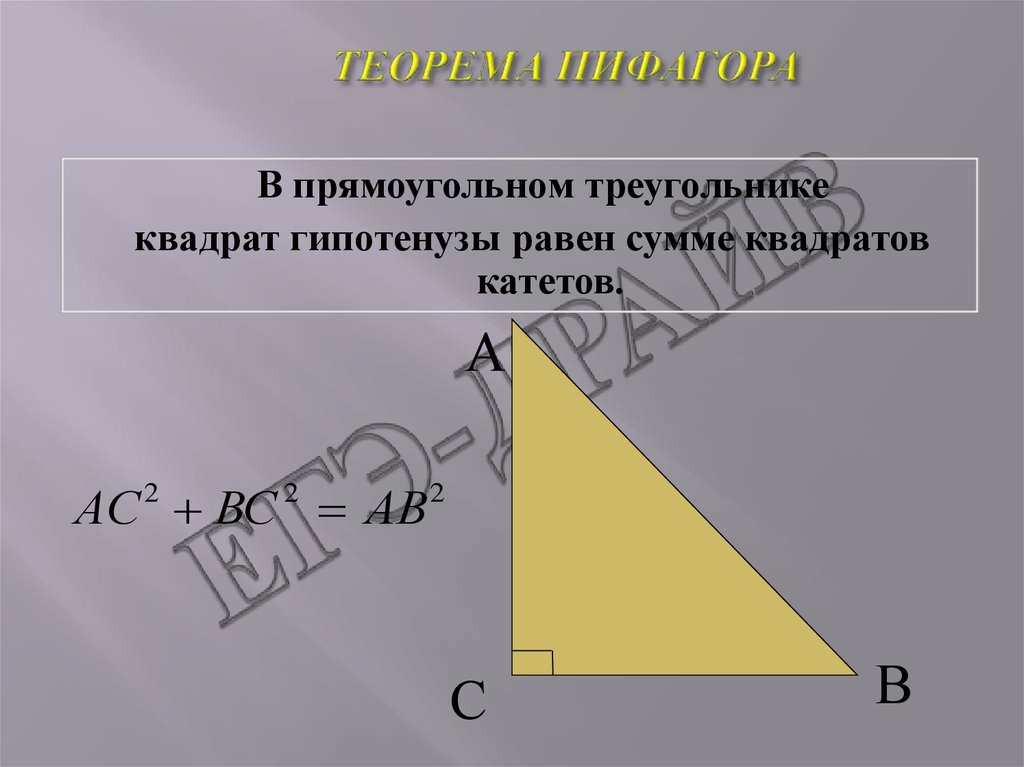
3. ТЕОРЕМА ПИФАГОРА

В прямоугольном треугольнике
квадрат гипотенузы равен сумме квадратов
катетов.
А
АС 2 ВС 2 АВ 2
С
В

4. Сумма острых углов прямоугольного треугольника равна 90

А
С = 90
А+ В = 90
С
В
sin A cos B

5.

А
Если
катет
прямоугольного
треугольника
равен
половине
гипотенузы, то угол, лежащий против
этого катета, равен 30 .
АС=АВ/2
Катет прямоугольного треугольника,
лежащий против угла в 30 , равен
половине гипотенузы.
С
30
В

6.

Высота прямоугольного треугольника, проведённая
из вершины прямого угла, есть среднее
пропорциональное между проекциями катетов на
гипотенузу.
ac
a
h ac bc
bc
h
b
h ac bc
2

7.

Катет прямоугольного треугольника есть среднее
пропорциональное между гипотенузой и проекцией
этого катета на гипотенузу.
ac
a
c
bc
h
b
a ac c
2
a ac c
b bc c
b bc c
2

8.

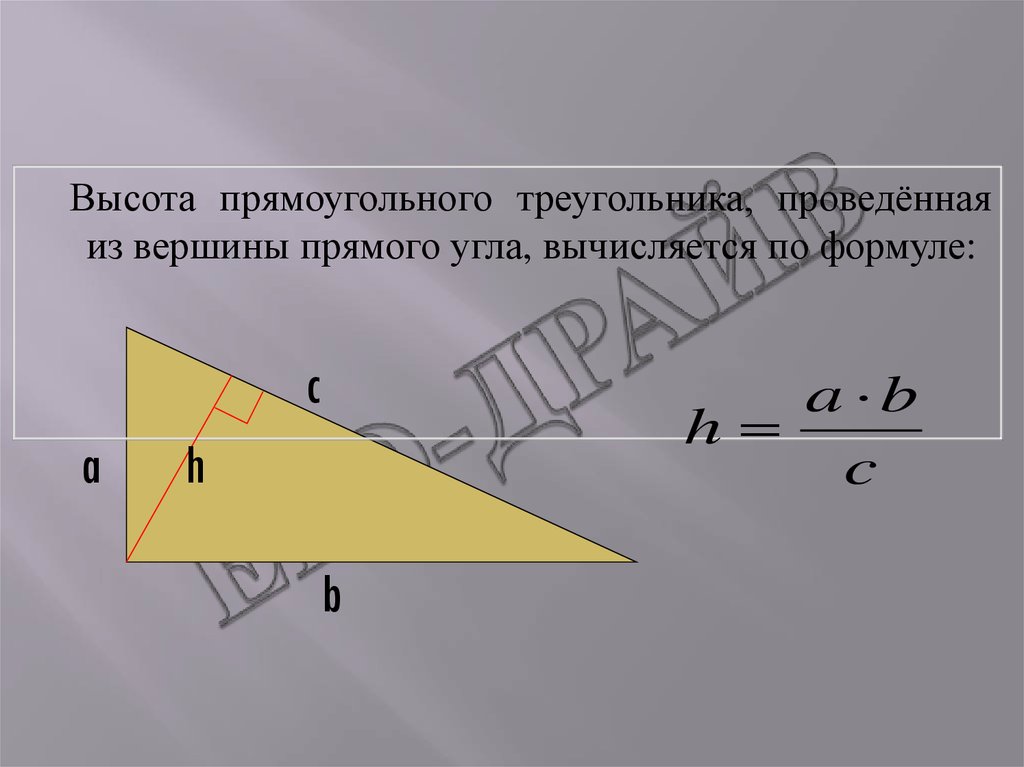
Высота прямоугольного треугольника, проведённая
из вершины прямого угла, вычисляется по формуле:
c
a
a b
h
c
h
b

9.

противолежащий катет
sin А
гипотенуза
А
прилежащий катет
cos А
гипотенуза
противолежащий катет
tgА
прилежащий катет
прилежащий катет
сtgА
противолежащий катет
С
В

10.

Площадь
прямоугольного треугольника
1
S a b
2
c
a
h
b
1
S c h
2

11.

Медиана
прямоугольного
треугольника,
проведённая из вершины прямого угла, равна
половине гипотенузы и равна радиусу описанной
около треугольника окружности.
a
c
m
b
c
m
2

12.

Радиус
описанной
около
прямоугольного
треугольника окружности лежит на середине
гипотенузы и равен ее половине:
c
R
2
в прямоугольный
Радиус вписанной
треугольник
окружности вычисляется по формуле:
a b c
r
2
Радиусы вписанной и описанной окружностей
прямоугольного
треугольника
связаны
соотношением:
a b
R r
2