Similar presentations:
Кинематика поступательного движения (лекция 1)
1.
Сегодня: воскресенье, 16 октября 2022 г.Лекция 1
Кинематика поступательного
движения
2.
Траектория движения материальнойточки – линия, описываемая этой точкой
в пространстве.
В зависимости от формы траектории
движение
может
быть
прямолинейным
(поступательным),
криволинейным
и
вращательным.
3.
4.
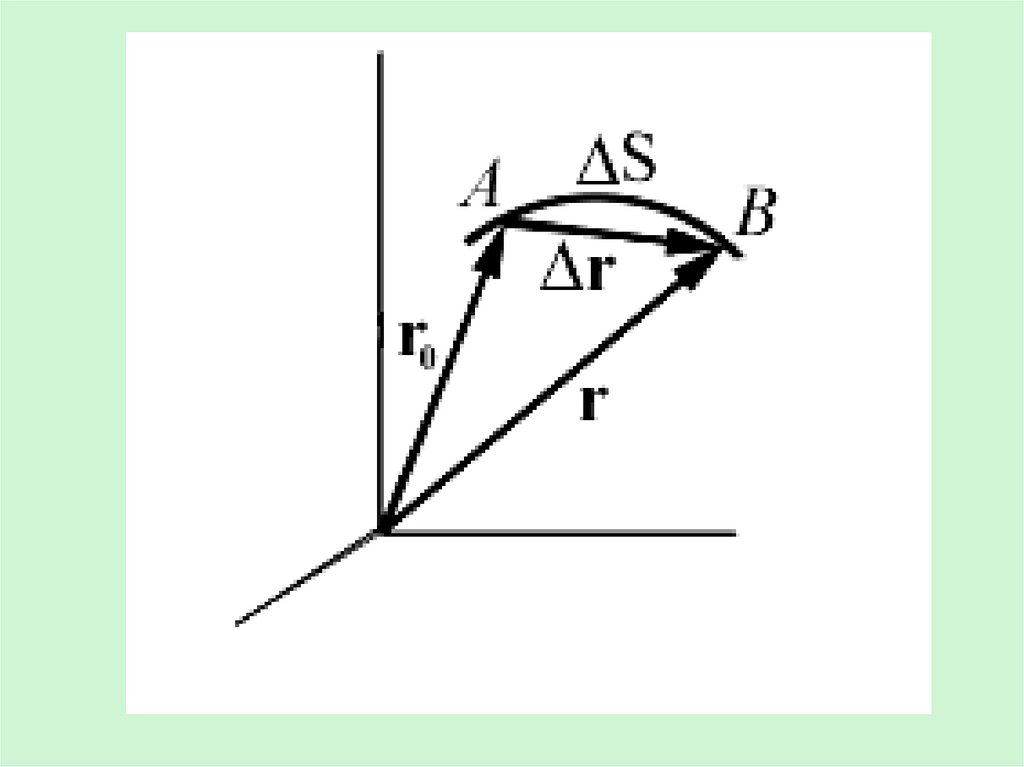
Длина участка траектории АВ, пройденногоматериальной точкой с момента начала отсчета
времени, называется длиной пути ∆S и является
скалярной функцией времени: ∆S=∆S(t).
r r - r0
Вектор
, проведенный из
начального положения движущейся точки в
положение ее в данный момент времени
(приращение
радиуса
–
вектора
за
рассматриваемый
промежуток
времени)
называется перемещением
r r - r0 (x - x 0 ) i + (y - y0 ) j + (z - z 0 )k.
5.
При прямолинейном движении векторперемещения
совпадает
с
соответствующим участком траектории
и модуль перемещения | r | равен
пройденному пути ∆S.
6.
Для характеристики движенияматериальной точки вводится векторная
величина - скорость, которой
определяется как быстрота движения, так
и его направление в данный момент
времени. Пусть материальная точка
движется по какой–либо криволинейной
траектории так, что в момент времени
t
ей
соответствует радиус–вектор r0
7.
СкоростьСКОРОСТЬ
Для характеристики движения
материальной точки вводится векторная
величина - скорость, которой
определяется как быстрота движения, так
и его направление в данный момент
времени.
Пусть материальная точка движется по
какой–либо криволинейной траектории так,
что в момент времени
t ей соответствует
радиус–вектор r0
8.
9.
υ >Вектором средней скорости <
называется отношение приращения радиуса–
вектора точки к промежутку времени :
r
υ
.
t
Направление вектора средней
скорости
совпадает с направлением r
. При
неограниченном уменьшении интервала времени
средняя скорость стремится к
предельному
значению, которое
называется мгновенной
скоростью υ :
10.
Δr drυ lim
.
Δt 0 Δt
dt
Мгновенная скорость – векторная величина, равная
скорости материальной точки в фиксированный
момент времени.
Мгновенная скорость – векторная величина,
равная первой производной радиуса – вектора
движущейся точки по времени.
Вектор скорости υ направлен по касательной
к траектории в сторону движения, поэтому
модуль мгновенной скорости равен:
11.
rr
S dS
υ | υ | lim
lim
lim
.
t 0 t
t 0 t
t 0 t
dt
Таким образом, модуль мгновенной скорости
равен первой производной пути по времени:
dS / dt
При
неравномерном
движении
модуль
мгновенной скорости с течением времени
изменяется. В данном случае пользуются
скалярной величиной < >– средней скоростью
неравномерного движения
< >=∆S/∆t.
12.
Если выражение dS= dt проинтегрироватьпо времени в пределах от t до t+∆t, то найдем
длину пути, пройденного точкой за время ∆t:
t t
S dt.
t
В случае равномерного движения:
t t
S dt t.
t
13.
Длинапути,
пройденного
точкой
за
промежуток времени от t1 до t2 дается
интегралом:
t2
S (t )dt.
t1
14.
Ускорение и его составляющиеФизической величиной,
характеризующей быстроту изменения
скорости по модулю и направлению является
ускорение.
Рассмотрим плоское движение.
Пусть вектор υ задает скорость точки А в
момент времени t. За время t движущаяся
точка перешла в положение В и приобрела
скорость, равную
υ1 υ dυ
15.
Среднимускорением
неравномерного
движения в интервале от t до t+∆t называется
векторная
величина,
равная
отношению
изменения скорости к интервалу времени:
a υ/ t.
Мгновенным
ускорением
(ускорением)
материальной точки в момент времени t будет
предел среднего ускорения:
υ dυ
a lim a lim
.
t 0
t 0 t
dt
16.
Тангенциальнаяускорения
составляющая
d
a lim
lim
,
t 0 t
t 0 t
dt
т.е. равна первой производной по времени от модуля
скорости, определяя тем самым быстроту изменения
скорости по модулю.
Вторая составляющая ускорения, равная
n
an lim
,
t 0 t
r
2
называется нормальной составляющей ускорения и
направлена по нормали к траектории к центру ее
кривизны (поэтому ее называют также центростремительным ускорением).
17.
Полное ускорение тела есть геометрическаясумма
тангенциальной
и
нормальной
составляющих:
dυ
a
a a n .
dt
18.
Итак, тангенциальная составляющаяускорения характеризует быстроту
изменения
скорости
по
модулю
(направлена
по
касательной
к
траектории),
а
нормальная
составляющая ускорения – быстроту
изменения скорости по направлению
(направлена
к
центру
кривизны
траектории).
19.
В зависимости от тангенциальной инормальной составляющих ускорения
движение
можно
классифицировать
следующим образом:
1. a =0, an =0 – прямолинейное
равномерное движение;
2. a = a =const, an =0 – прямолинейное
равнопеременное движение.
При таком виде движения
2 1
a a
.
t
t2 t1
20.
Если начальный момент времени t1=0, аначальная скорость 1 0 , то, обозначив
t2=t
2 ,
a ( 0 ) / t ,
и
получим
откуда
0 at.
Проинтегрировав эту формулу в пределах от
нуля до произвольного момента t,
найдем, что длина пути пройденного точкой,
в случае равнопеременного движения
t
t
S dt 0 at dt 0t at / 2;
2
0
0
21.
3. a =f(t), an =0 – прямолинейное движение спеременным ускорением.
4. a =0,an =const. При a =0 скорость по модулю
не меняется, а изменяется по направлению. Из
2
a
формулы
/r следует, что радиус
n =
кривизны
должен
быть
постоянным.
Следовательно, движение по окружности
является равномерным.
5. a =0, an 0 – равномерное криволинейное
движение.
6. a =const, an 0 – криволинейное равнопеременное движение.




















 physics
physics








