Similar presentations:
Основные теоремы о пределах
1.
Основные теоремы о пределахРассмотрим теоремы, которые облегчают нахождение пределов
функций.
Формулировка теорем, когда x x0 или x аналогичны,
поэтому будем пользоваться обозначением: lim f ( x ).
Предел суммы (разности) двух функций равен сумме (разности)
пределов:
lim f1( x ) f2 ( x ) lim f1( x ) lim f2 ( x )
Предел произведения двух функций равен произведению
пределов:
lim f1( x ) f2 ( x ) lim f1( x ) lim f2 ( x )
Постоянный множитель можно выносить за знак предела:
lim C f ( x ) C lim f ( x )
2.
Основные теоремы о пределахПредел дроби равен пределу числителя, деленному на предел
знаменателя, если предел знаменателя не равен нулю:
f1( x ) lim f1( x )
lim
f2 ( x ) lim f2 ( x )
lim f ( x ) 0
2
Предел степени с натуральным показателем равен той же
степени предела:
lim f ( x ) lim f ( x )
n
n
Предел показательно – степенной функции:
lim f ( x )
g(x)
lim f ( x )
lim g ( x )
3.
Вычисление пределовВычисление предела:
lim
f
(
x
)
A
x x
0
начинают с подстановки предельного значения x0 в функцию f(x).
Если при этом получается конечное число, то предел равен этому
числу.
3x 1
3 1 1
lim
2
2
2
x 1
x
1
Если при подстановки предельного
значения x0 в функцию f(x) получаются
выражения вида:
то предел будет равен:
C
0
C
0
4.
Вычисление пределовЧасто при подстановке предельного значения x0 в функцию f(x)
получаются выражения следующих видов:
0
;
0
; 0 ; 1 ; 0 0 ; 0 ;
Эти выражения называются неопределенности, а вычисление
пределов в этом случае называется раскрытие
неопределенности.
5.
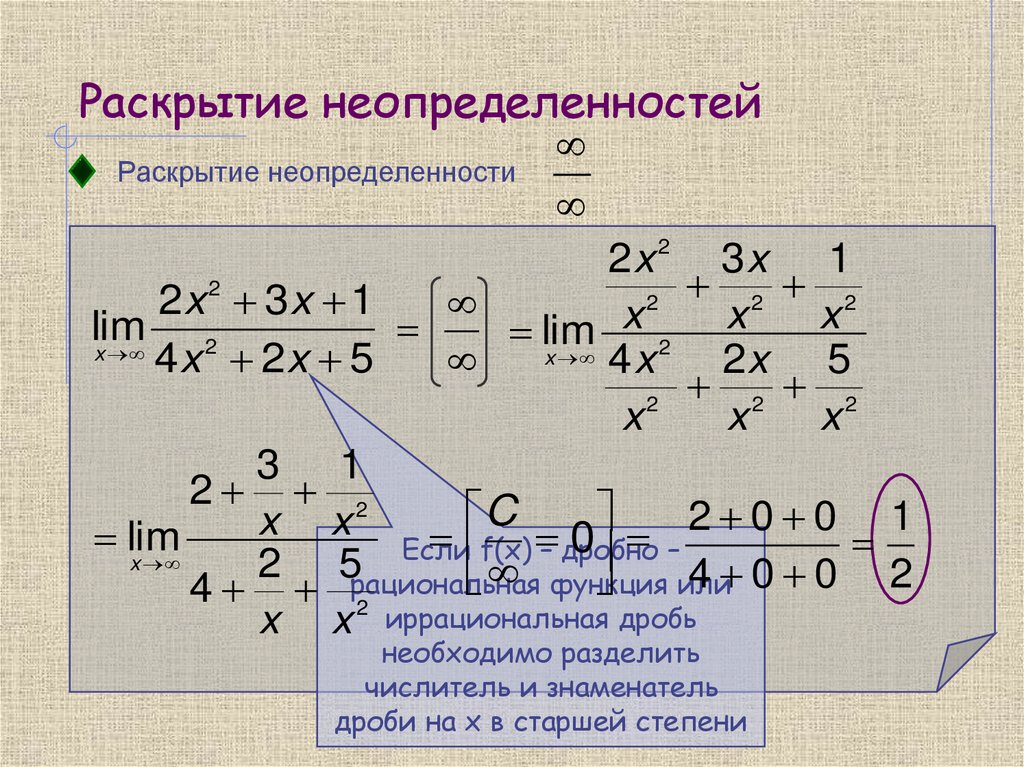
Раскрытие неопределенностейРаскрытие неопределенности
2x 2 3 x 1
2 2
2
2x 2 3 x 1
x
x
x
lim
lim
x
x 4 x 2
4 x 2 2x 5
2x 5
2 2
2
x
x
x
3 1
2 2
C
2 0 0 1
x
x
lim
f(x) – дробно
0 –
Если
x
2 5рациональная
4 0 0 2
функция
или
4 2
x x иррациональная дробь
необходимо разделить
числитель и знаменатель
дроби на x в старшей степени
6.
Найти пределы указанныхфункций
7.
Раскрытие неопределенностейРаскрытие неопределенности
0
0
x 2 14 x 32
0
x 2 x 16
lim
lim
2
x 2
x 2
x 6x 8
0
x 2 x 4
x 16 18
lim
9
x 2
x 4
2
Если f(x) – дробно –
рациональная
x 1 1 x 1 1
0
x 1 1 функция,
необходимо разложить
наlim
lim
Если f(x) – иррациональная
x 0
x 0
0
x
множители
числитель
и
x 1 умножить
1
дробь, x
необходимо
знаменатель дроби
числитель и знаменатель
x 1 1
1дроби на выражение,
1
lim
lim
числителю.
x 0
x 0
сопряженное
x x 1 1
x 1 1 2
8.
Найти пределы указанныхфункций
9.
Раскрытие неопределенностейРаскрытие неопределенности
2
2
lim
x
1
x
1
x
x 1 x 1 x 1 x 1
lim
x 1 x 1
2
x
lim
x
2
2
2
2
2
Умножим и разделим
2
( x 1) ( x функцию
1)
на
сопряженное
lim
2
x
2
2
выражение.
2
2
x 1 x 1
2
0
x 1 x 1
2
10.
Найти пределы указанныхфункций
11.
№ варианта1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Ф.И.О обучающегося
Аджем Юрий Сергеевич
Балабеков Балабек Исаевич
Бачиев Алексей Александрович
Бессонов Даниил Юрьевич
Вилькишов Иван Николаевич
Дагаев Ислам Лом-Алиевич
Дворниченко Евгений Сергеевич
Ильина Полина Анатольевна
Кузнецов Иван Олегович
Макшанцев Валерий Сергеевич
Москаев Артём Сергеевич
Начмутдинов Руслан Ренатович
Некрасов Алексей Юрьевич
Осокин Илья Евгеньевич
Пекуров Петр Антонович
Подколзин Александр Михайлович
Сибер Яков Михайлович
Сосновский Дмитрий Сергеевич
Столярова Анастасия Геннадьевна
Тарханова Ольга Сергеевна
Усманов Максим Александрович
Хайрулин Сергей Евгеньевич
Хамидов Алишер Туйчибоевич
Чинякин Вячеслав Викторович
Щепина Ольга Павловна
12.
https://www.kstu.kz/wpcontent/uploads/docs/restricted/lib/portfolio/folder/rus/matematika/ryab
ushko1.pdf
13.
Первый замечательный пределsin x
lim
1
x 0
x
Следствия:
x
lim
1
x 0
sin x
tgx
lim
1
x 0
x
x
lim
1
x 0
tgx
sin kx
lim
1
x 0
kx
14.
Первый замечательный предел0
1 cos 4 x
2 sin 2x
sin 2 x
lim
lim
2 lim
2
2
x 0
x
0
x
0
0
x
x
x
2
2
sin 2 x 2 lim 2 sin 2 x
x 0
2 lim
2x
x 0 x
2
2
sin 2 x
2
2 2 lim
2 2 1 8
x 0
2x
2
15.
Найти пределы указанныхфункций
16.
Второй замечательный пределВторым замечательным пределом называется равенство:
Следствия:
2.7182818284
1
x
1
lim
1
e
x
x
x e
lim
1
x
x 0
kx
1
lim
1
e
x
kx
Второй замечательный предел применяется для раскрытия
неопределенности 1 .
Другие полезные формулы:
(1 x ) 1
lim
m
x 0
x
m
ln( 1 x )
lim
1
x 0
x
ax 1
lim
ln a
x 0
x
17.
Второй замечательный пределx 3
x 1 4
lim
lim
x
x
x 1
x 1
x 3
4
1
x 1 y
1
1
lim
y
y
x 3
4
lim
1
x
x 1
x 4 y 1; x ; y
4 y 1 3
4y
1
1
1 1
lim
y
y
y
4
4
4
1
1
1 lim 1 e 4 14 e 4
lim
y
y
y
y
y
x 3
18.
Найти пределы указанныхфункций
19.
https://www.kstu.kz/wpcontent/uploads/docs/restricted/lib/portfolio/folder/rus/matematika/ryab
ushko1.pdf
20.
Бесконечно малые функцииФункция y = f(x) называется бесконечно малой при
x x0
( x )
если
lim f ( x ) 0
x x0
x
Бесконечно малые функции часто называют бесконечно малыми
величинами; обозначают обычно греческими буквами α, β и т. д.
Например:
sin x 0
lim
x 0
( x ) sin x - бесконечно малая функция при x 0
Теорема
Если функция y = f(x) имеет предел, равный А, то ее можно
представить как сумму числа А и бесконечно малой функции α(x)
lim
f
(
x
)
A
x x
0
f ( x ) A ( x )
21.
Бесконечно малые функцииСравнение бесконечно малых
Пусть α(х), β(х) – бесконечно малые функции
Если
( x )
lim
0
x x0
( x )
то говорят, что α(х) является бесконечно малой высшего
порядка по сравнению с β(х) : o( )
Если
( x )
lim
m
x x0
( x )
( m 0)
то говорят, что α(х) и β(х) – бесконечно малые одного и того
же порядка.
Если
( x )
lim
1
x x0
( x )
то α(х) и β(х) – эквивалентные
бесконечно малые ~
22.
Бесконечно малые функцииПолезно иметь в виду эквивалентность следующих бесконечно
малых при x 0
m
sin x ~ x;
e x 1 ~ x;
1 x 1 ~ mx
;
x
tgx ~ x;
a 1 ~ x ln a;
x2
1 cos x ~ .
arcsin x ~ x; ln x 1 ~ x;
2
arctg x ~ x; loga x 1 ~ x loga e;
sin x
0
lim
x 0 4
0
1 x 1
x
lim
4
x 0
0.25 x
sin x ~ x
1
1
1 x 4 1 ~ x
4





















 mathematics
mathematics








