Кинематика вращательного движения. Лекция 2

1.

Сегодня: вторник, 11 октября 2022 г.
Лекция 2
Кинематика вращательного
движения

2.

Движение твердого тела, при котором две
его точки О и О' остаются неподвижными,
называется вращательным движением вокруг
неподвижной оси, а неподвижную прямую ОО'
называют осью вращения.
Пусть абсолютно
твердое тело вращается
вокруг
неподвижной
оси ОО' .

3.

Угол поворота характеризует перемещения всего
тела за время dt.
Удобно ввести dφ – вектор элементарного поворота
тела, численно равный углу поворота и направленный
вдоль оси вращения ОО' так, чтобы глядя вдоль вектора
мы видели вращение по часовой стрелке.
Векторы, направления которых связываются с
направлением вращения, называются псевдовекторами
или аксиальными векторами.
Эти векторы не имеют определённых точек приложения:
они могут откладываться из любой точки оси вращения.

4.

Элементарные повороты удовлетворяют обычному
правилу сложения векторов:
dφ dφ dφ .
Угловой скоростью ω называется вектор
1
2
численно равный первой производной от угла
поворота по времени и направленный
вдоль
оси
вращения в направлении dφ ( ω и dφ всегда
направлены в одну сторону).
dφ
ω
dt

5.

Пусть – линейная скорость точки М. За
промежуток времени dt точка М проходит путь
dr dt. В то же время dr Rd
(центральный угол). Тогда,
dr Rd
υ
dt
dt
или в векторной форме
ωR
[ , R ]

6.

Вектор ортогонален к векторам ω и R
и направлен в ту же сторону, что и векторное
произведение [ , R .]
Период Т – промежуток времени, в
течение которого тело совершает полный
оборот (т.е. поворот на угол 2
).
Частота ν – число оборотов тела за
1 секунду.
1
ν .
Т

7.

При вращении с угловой скоростью ω,
имеем:
2π
ω
2 πν;
Т
2π
Т ;
ω
Для характеристики неравномерного вращения тел
введем вектор углового ускорения ε :
dω
ε
dt

8.

Вектор ε направлен в ту же сторону, что
и ω при ускоренном вращении dω 0 ,
dt
и направлен в противоположную ω сторону при
замедленном вращении dω 0 .
dt
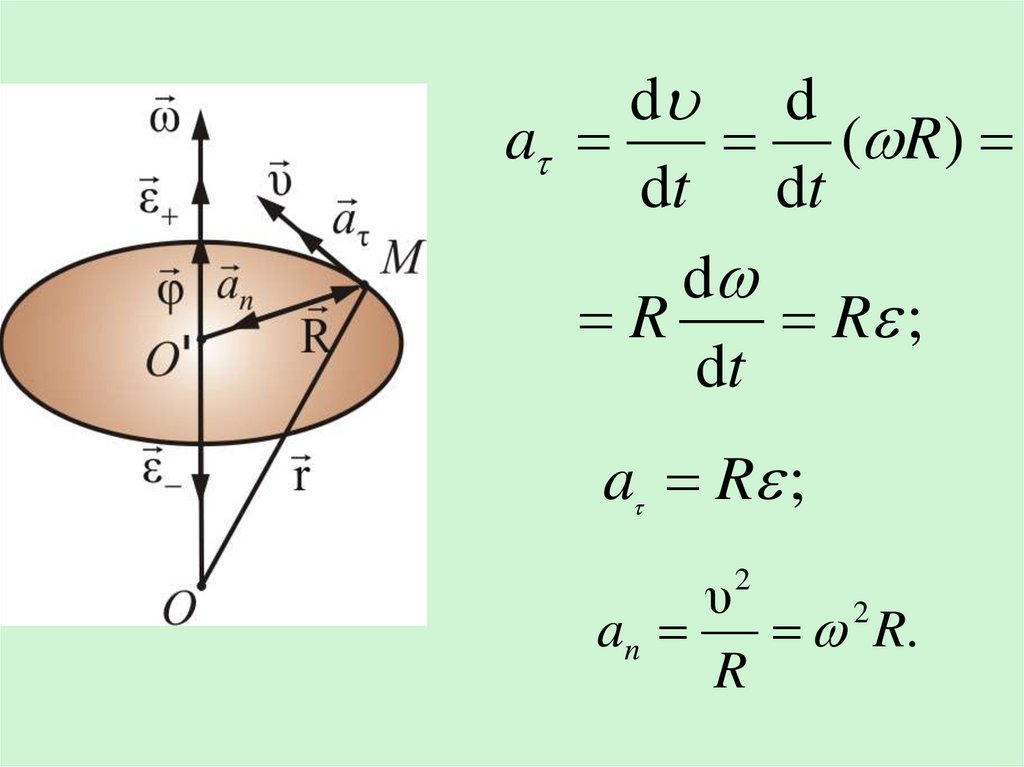
Как и любая точка твердого тела, точка М
имеет
нормальную
и
тангенциальную
составляющие ускорения. Выразим нормальное и
тангенциальное ускорения точки М через угловую
скорость и угловое ускорение:

9.

d d
a
( R )
dt dt
d
R
R ;
dt
a R ;
υ
2
an
R.
R
2

10.

Обратите
внимание.
Все
кинематические
параметры,
характеризующие вращательное движение
(угловое ускорение, угловая скорость и угол
поворота) направлены вдоль оси вращения.

11.

Формулы простейших случаев вращения тела
вокруг неподвижной оси:
- равномерное вращение 0; const;
- равнопеременное
вращение const;
0 t;
t
0t
0
t
2
2