Similar presentations:
Систематические погрешности
1.
Систематические погрешностиQ / [Q] = X;
Данное уравнение называют уравнением измерения.
Q – размер измеряемой физической величины,
[Q] – размер физической величины, принятой за единицу.
X – оценка физической величины
Истинное значение физической
величины Q
Δ=X –Q
Δ - погрешность результата
измерения
Действительное значение
физической величины X
Δ = Δс + Δсл
Δс – систематическая составляющая погрешности
Δсл – случайная составляющая погрешности
2.
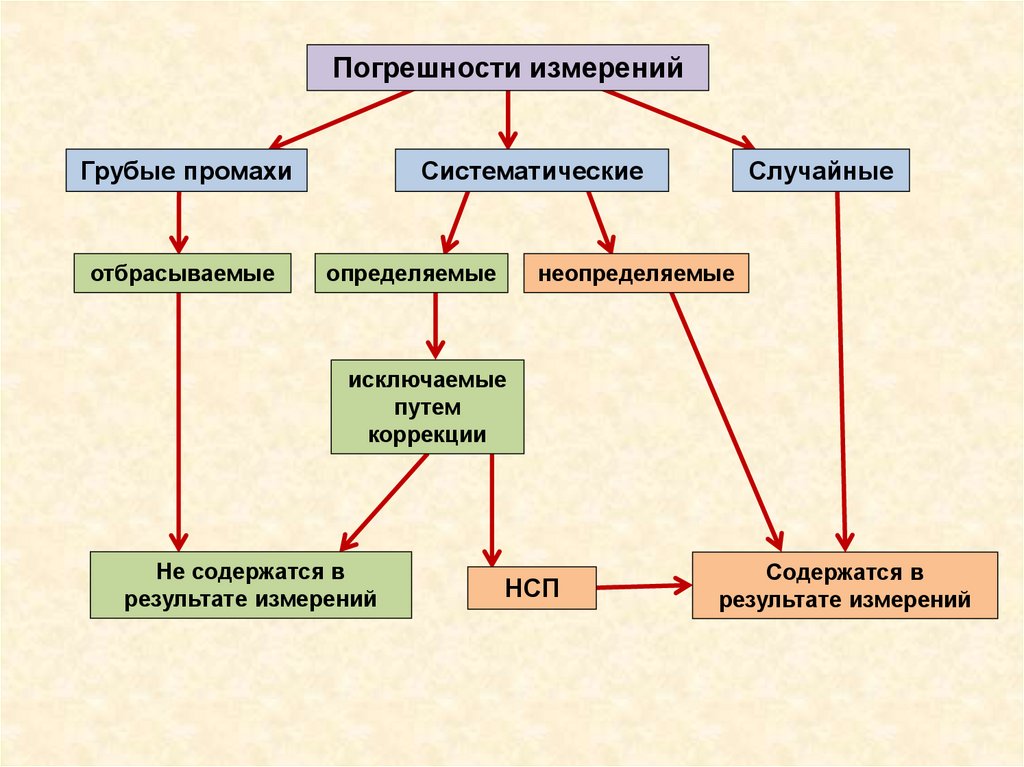
Погрешности измеренийГрубые промахи
отбрасываемые
Систематические
определяемые
Случайные
неопределяемые
исключаемые
путем
коррекции
Не содержатся в
результате измерений
НСП
Содержатся в
результате измерений
3.
Систематическаяпогрешность
измерений
–
составляющая
погрешности результата измерения, остающаяся постоянной или же
закономерно изменяющаяся при повторных измерениях одной и той
же физической величины.
Систематические
погрешности
могут
быть
предсказаны,
обнаружены и исключены из результата измерений (уменьшены)
путем введения соответствующих поправок.
Аддитивные систематические погрешности
Мультипликативные систематические погрешности
4.
Задачаобеспечения
правильности
измерений
должна
предусматривать обнаружение, оценку и уменьшение (или
полное исключение) систематических погрешностей.
Правильность измерений – качество измерений, отражающее
близость к нулю систематической погрешности .
5.
Систематические погрешностиВ зависимости от причин возникновения:
1. инструментальные
2. внешние
3. личные
4. погрешности метода (методические погрешности)
По характеру проявления:
1. Постоянные
2. Переменные
3. Дрейфовые
6.
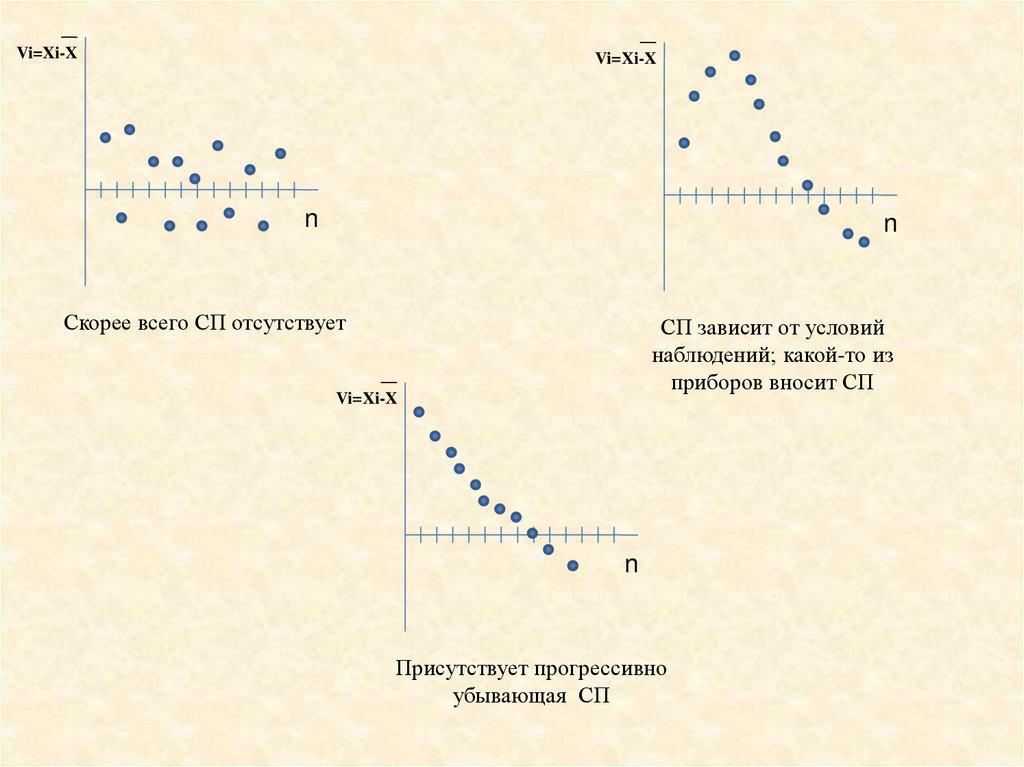
Vi=Xi-XVi=Xi-X
n
n
Скорее всего СП отсутствует
СП зависит от условий
наблюдений; какой-то из
приборов вносит СП
Vi=Xi-X
n
Присутствует прогрессивно
убывающая СП
7.
Методы исключения и компенсации систематических погрешностейНеисправленный результат измерения – это значение физической величины,
полученное в результате измерения до введения поправок.
Исправленный результат измерения – это значение физической величины, полученное
в результате измерений и уточненное путем введения в него необходимых поправок.
поправка – это значение величины, вводимое в неисправленный результат измерения с
целью исключения составляющих систематической погрешности.
Q = X + Ca
(Численное значение Са может быть как со знаком «+», так и со знаком « - » ).
поправочный множитель – это числовой коэффициент, на который умножают
неисправленный результат измерения с целью исключения влияния систематической
погрешности.
Q = Cm X,
где Cm – поправочный множитель.
8.
При оценке и исключении систематических погрешностей впервую
очередь
рассматриваются
возникающие вследствие влияния:
1) объекта измерения,
2) субъекта,
3) средств измерения,
4) методов и способов измерения,
5) условий измерения.
систематические
эффекты,
9.
До начала измерений рекомендуется:1. тщательно устанавливать нулевое показание и калибровать СИ;
2. применять только предварительно поверенные СИ.
3. прогревать приборы в течение времени, указанного в инструкции по
эксплуатации;
4. применять при сборке короткие соединительные провода, а на высоких
частотах коаксиальные кабели;
5. прибегать при необходимости к экранированию и термостатированию,
осуществлять амортизацию прибора, чтобы устранить вибрации и сотрясения;
6. правильно размещать СИ (устанавливать в рабочее положение, размещать
вдали от источников тепла и электромагнитных полей и т.п.),
10.
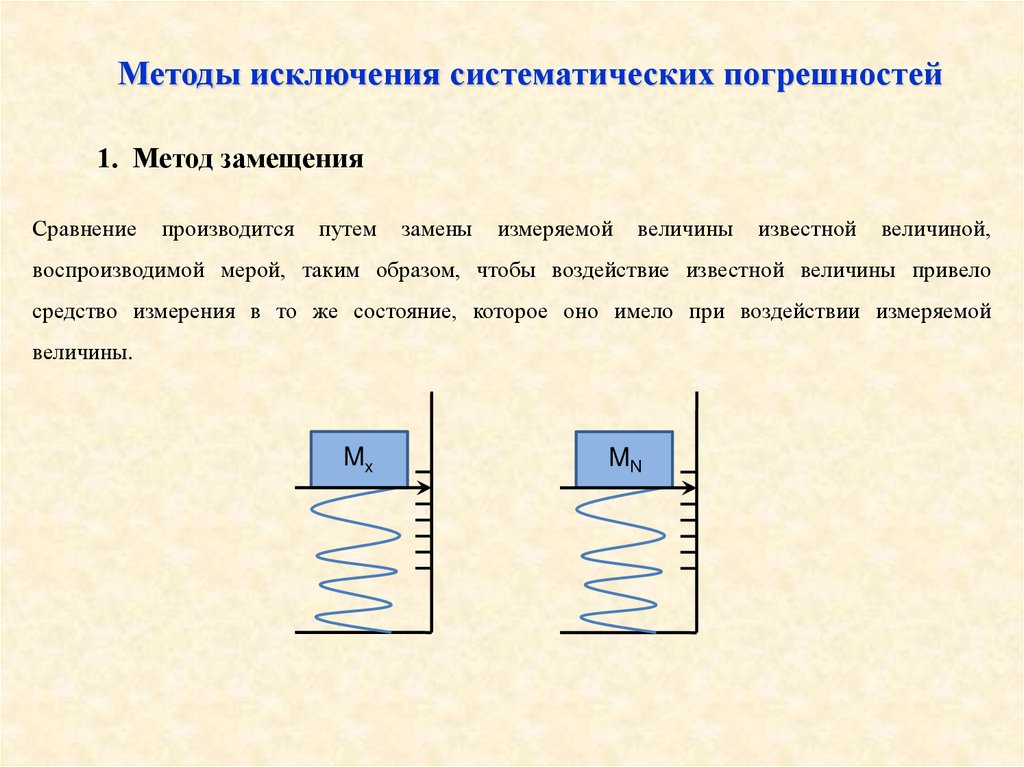
Методы исключения систематических погрешностей1. Метод замещения
Сравнение
производится
путем
замены
измеряемой
величины
известной
величиной,
воспроизводимой мерой, таким образом, чтобы воздействие известной величины привело
средство измерения в то же состояние, которое оно имело при воздействии измеряемой
величины.
Mx
MN
11.
2. Метод компенсации погрешности по знаку● измерение проводят дважды таким образом, чтобы систематическая погрешность
(неизвестная по абсолютному значению, но известная по своей природе) входила в результаты
наблюдений с противоположными знаками. Тогда полусумма результатов измерений будет
свободна от этой погрешности.
Q1 = Q + Θ;
Q2 = Q – Θ;
Q = 0,5 (Q1 + Q2).
Q1 и Q2 – результаты двух измерений, Θ –систематическая погрешность,
Q – значение измеряемой величины, свободное от погрешности.
● систематическая погрешность входит в показания средства измерений с одинаковым
знаком, но сам эксперимент ставится так, что меняет знак искомое значение Q, оставаясь
неизменным по абсолютной величине.
Q1 = Q + Θ;
Q2 = -Q + Θ;
Q = 0,5 (Q1 - Q2).
12.
3. Метод противопоставления (перестановки)измерения проводят два раза, причем причина, вызывающая погрешность при первом
измерении, оказывает противоположное действие на результат второго измерения.
L1
L2
MN
Mx
Если L1 ≠L2
Mx L1 = MN L2
Δс = MN [ (L2/L1) - 1]
Mx L1 = MN1 L2
MN2 L1 = Mx L2
Mx = √ MN1 ∙ MN2
условие равновесия
13.
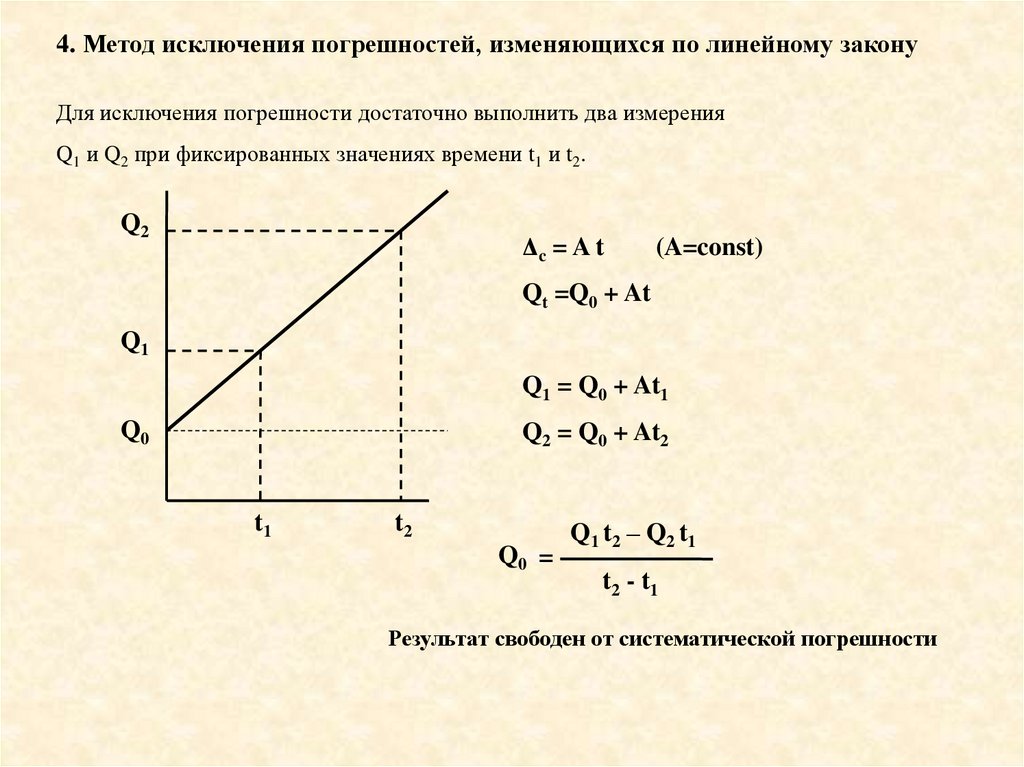
4. Метод исключения погрешностей, изменяющихся по линейному законуДля исключения погрешности достаточно выполнить два измерения
Q1 и Q2 при фиксированных значениях времени t1 и t2.
Q2
Δc = A t
(A=const)
Qt =Q0 + At
Q1
Q1 = Q0 + At1
Q0
Q2 = Q0 + At2
t1
t2
Q0 =
Q 1 t2 – Q 2 t 1
t2 - t1
Результат свободен от систематической погрешности
14.
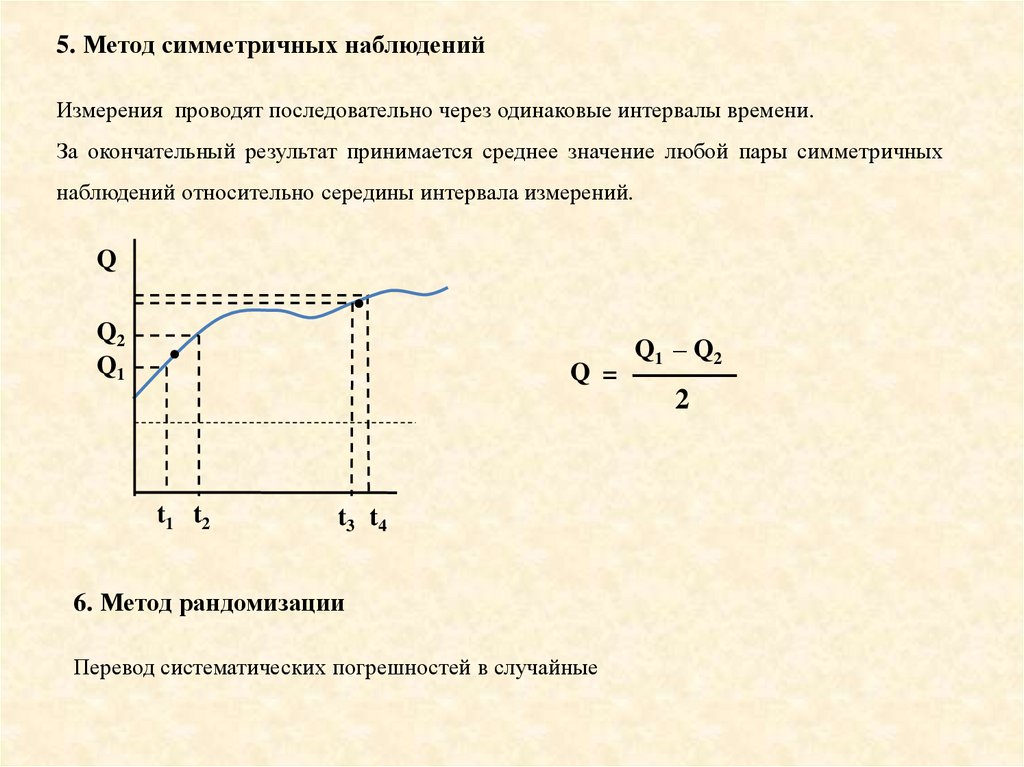
5. Метод симметричных наблюденийИзмерения проводят последовательно через одинаковые интервалы времени.
За окончательный результат принимается среднее значение любой пары симметричных
наблюдений относительно середины интервала измерений.
Q
Q2
Q1
Q =
Q1 – Q2
2
t1 t2
t3 t4
6. Метод рандомизации
Перевод систематических погрешностей в случайные
15.
Случайные погрешностиСлучайные погрешности неопределенны по своему значению и знаку и поэтому не могут
быть исключены из результатов измерений, как систематические погрешности.
Случайной называют такую величину, которая в результате опыта может
принимать то или иное значение, неизвестно заранее - какое именно.
Дискретные случайные величины – принимающие отделенные друг от
друга значения, которые можно заранее перечислить.
Непрерывные случайные величины - величины, возможные значения
которых непрерывно заполняют некоторый промежуток.
16.
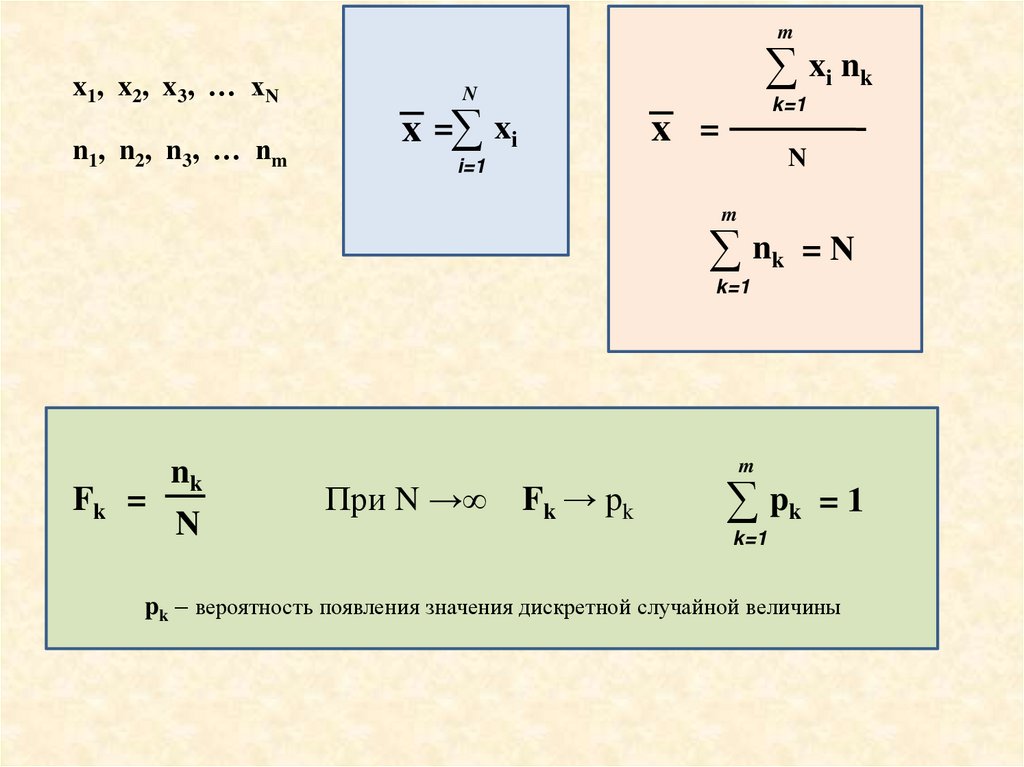
mx 1 , x 2 , x 3 , … xN
n1, n2, n3, … nm
∑ xi nk
N
x =∑ xi
k=1
x =
N
i=1
m
∑ nk
=N
k=1
Fk =
nk
N
m
При N →∞
Fk → pk
∑ pk
=1
k=1
pk – вероятность появления значения дискретной случайной величины
17.
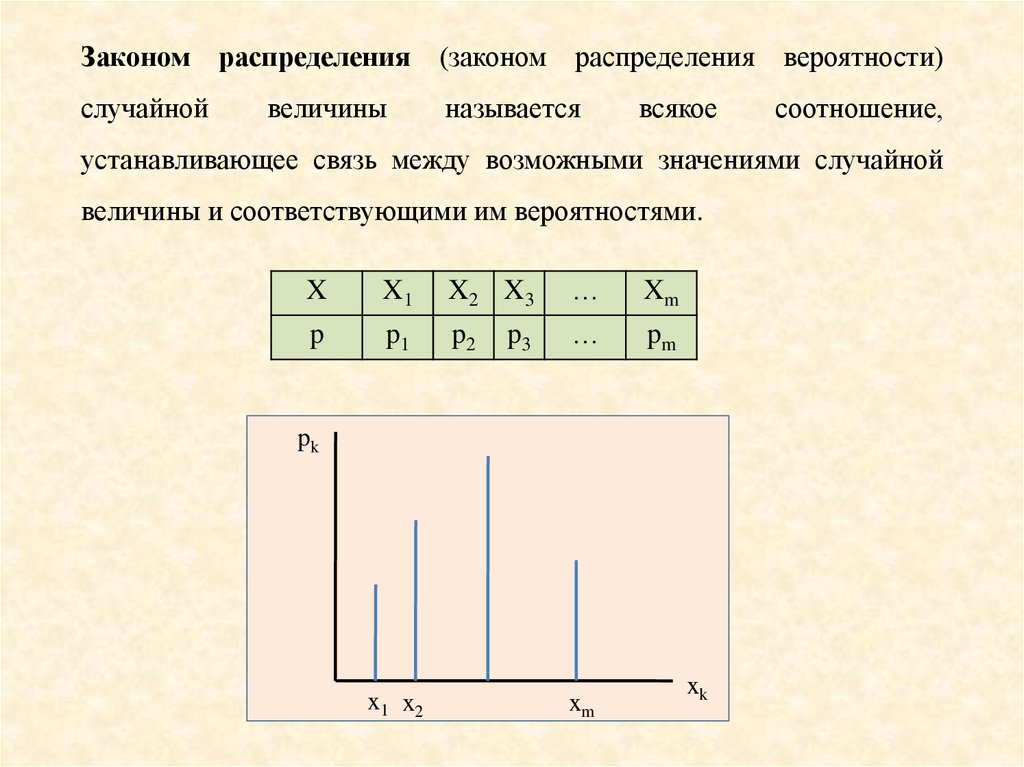
Закономслучайной
распределения (законом
величины
распределения
называется
всякое
вероятности)
соотношение,
устанавливающее связь между возможными значениями случайной
величины и соответствующими им вероятностями.
X
X1
X2 X3
…
Xm
p
p1
p2
…
pm
p3
pk
x1 x2
xm
xk
18.
Числовые характеристики случайной величины:Математическое ожидание
N
M(x) = x1 p1 + x2 p2 + …+ xN pN =∑ xi pi
i=1
оценкой математического ожидания является среднее арифметическое
Дисперсия - математическое ожидание квадрата отклонения случайной величины
от ее математического ожидания
N
D(x) = M [X – M(x)]2 =∑ [xi - M(x)]2 pi
i=1
Среднее квадратическое отклонение (СКО)
σx = √ D











 mathematics
mathematics








