Similar presentations:
Представление числовой информации с помощью систем счисления
1.
Д/з №1 к следующей сессии:•составьте и оформите в MS Word (можно рукописно)
кроссворд по теме «Системы счисления» ( не менее 10 слов понятий, используемых в презентации)
2.
Знать понятия:Система счисления, цифра, число, основание системы счисления,
разряд, алфавит, непозиционная система счисления, позиционная
система счисления, единичная (унарная) система счисления.
Научиться записывать:
десятичное число в римской системе счисления,
любое число в позиционной системе счисления в развернутой
форме
Уметь:
определять основание системы счисления
приводить примеры чисел различных позиционных систем
счисления
объяснить разницу между числом и цифрой позиционной и
непозиционной системой счисления
3.
Задание 1. (дистант)Выписать в тетрадь основные определения понятий:
1. Система счисления
2. Цифра
3. Число
4. Основание системы счисления
5. Разряд
6. Алфавит
7. Непозиционная система счисления (виды, достоинства,
недостатки)
8. Позиционная система счисления (виды, достоинства,
недостатки)
4. Задание 2. Переведите десятичные числа в двоичную систему счисления (представить решение, а не ответ)
27 =54 =
35 =
66 =
5. Задание 3. Переведите числа из двоичной системы счисления в десятичную
• 10110 2=1101012 =
6.
Система счисления- это знаковая система, в которой числа
записываются по определенным
правилам с помощью символов
некоторого алфавита, называемых
цифрами.
- совокупность правил для
чтения и записи чисел.
7.
Цифра, число, словарь?• Цифра - знак, принятый и используемый
для обозначения количества (числа).
• Число – это выражение количественных
характеристик в удобном виде,
посредством цифр.
• Цифра– это знак (символ),
• число – это количественная абстракция;
понятие, отражающее количество.
Алфавит — это множество символов или букв
8.
системы счисленияпозиционные
непозиционные
9.
Непозиционной называют системусчисления, в которой количественное
значение цифры не зависит от ее
положения в числе.
Примеры:
•единичная (палочная)
• десятичная древнеегипетская
• алфавитная система записи чисел
• римская
10. История чисел и систем счисления
• Проблема обозначения(кодирования) числовойинформации:
• Один (рыба-нож), много, меньше, больше;
• Разные племена (народы) – разные системы
счисления
• Первобытный человек – орудие счета –
десятичная система счисления
• Двенадцатеричная СС(Англия):
Система мер: 1 фут-12 дюймов
Денежная система: 1 шиллинг- 12 пенсов
Чайные, столовые сервизы
11. Единичная(палочная) система счисления
В древние времена, когда люди начали считать,появилась потребность в записи чисел..
Количество предметов изображалось
нанесением черточек, точек, засечек на какой-
либо твердой поверхности: камне, глине…
12. Древнеегипетская десятичная система счисления (2,5 тысяч лет до н.э.)- сложение
13. Древнеегипетская десятичная система счисления, умножение
собранный урожай в несколько раз больше,
чем количество посеянных семян.
Пример: 19 * 31
1
31
2
62
4
124
8
248
16
496
(19 = 1 + 2 + 16)
складывали числа, стоящие в отмеченных строках
справа (31 + 62 + 496 = 589)
14. Алфавитная система счисления
• Для записи чисел использовался буквенный алфавит.В славянский системе над буквой, обозначающей
цифру, ставился специальный знак – «титло».
Славянская система счисления сохранилась в
богослужебных книгах.
15. Римская система счисления
Применяется более 2500 лет.В качестве цифр используются латинские буквы:
I
1
V
5
X
10
L
C
50 100
D
M
500 1000
Например: CXXVIII = 100 +10 +10 +5 +1 +1 +1=128
Правила:
• Если меньшая цифра стоит слева от большей, то она
вычитается, IV
•если справа - прибавляется. VI
Запомните: 5, 50, 500 не повторяются!
I, X, C, M могут повторяться до 3-х раз.
16. Недостатки непозиционной системы счисления:
• Трудно записывать большие числанеобходимо вводить новые цифры (буквы);• Невозможно представлять дробные и
отрицательные числа;
• Нет нуля;
• Очень сложно выполнять арифметические
действия.
17.
Позиционной называют систему счисления, вкоторой количественное значение цифры
зависит от ее положения в числе.
Основные достоинства позиционной
системы счисления:
•Ограниченное количество символов для записи
чисел;
•Простота выполнения арифметических
операций.
18. Позиционная система счисления
Количество используемых цифр в системе счисленияназывается основанием.
Основание системы, к которой относится число, обозначается
подстрочным индексом к этому числу.
1110010012
356418
43B8D16
Пример: основание десятичной системы счисления =10
Позиция (место) цифры в числе называется разрядом
Число 555- свернутая форма.
2
1
555=5*10 + 5*10 +5*10
числа.
0
- развернутая форма
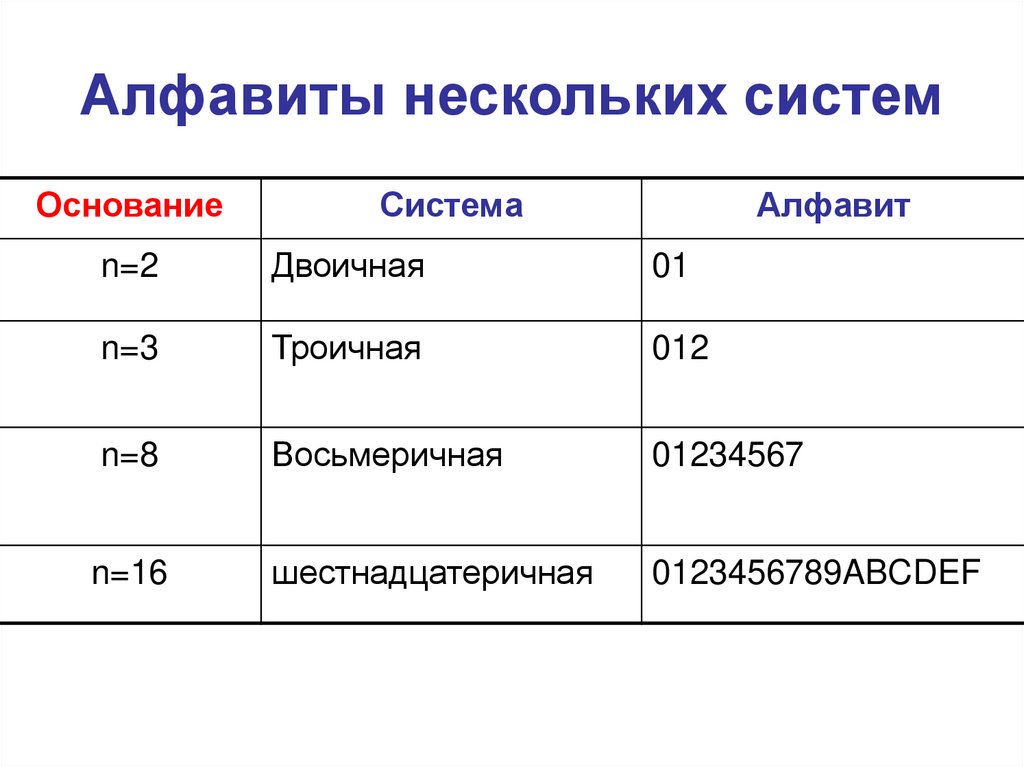
19. Алфавиты нескольких систем
ОснованиеСистема
Алфавит
n=2
Двоичная
01
n=3
Троичная
012
n=8
Восьмеричная
01234567
n=16
шестнадцатеричная
0123456789ABCDEF
20. Десятичная система счисления
Любое число мы можем записать при помощи десяти цифр:0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Известный русский математик Н.Н.Лузин так выразился по
этому поводу:
«Преимущества десятичной системы
счисления не математические, а
зоологические. Если бы у нас было на
руках не десять пальцев, а восемь, то
человечество бы пользовалось
восьмеричной системой счисления.»
21. Арабская нумерация
Возобладала при Петре IКак видоизменялись цифры, употреблявшиеся арабами,
пока они не приняли современные формы:
22. Двоичная система счисления
• придумана задолго до появления компьютеров –• зарождение связано с именем Г. В. Лейбница,
• ее недостаток – «длинная» запись чисел.
• наиболее употребительная в информатике,
вычислительной технике и смежных отраслях система
счисления. Использует две цифры: 0, 1
Пример:
Свернутая форма записи числа: 1012
210
Развернутая форма: 101 =1*22 +0*21+1*20 =5
Все числа в компьютере представляются с помощью нулей и
единиц, т. е. в двоичной системе счисления.
23. Представление чисел в позиционных системах счисления
разряды2 1 0 -1 -2
N
10
3 4 8, 1 2 = 3*102 + 4*101 + 8*100 + 1*10-1 + 2*10-2
=
Свернутая форма записи числа
развернутая форма записи числа
24. Перевод чисел в десятичную СС из других СС
Алгоритм перевода:1. Представьте число в развернутой форме.
При этом основание СС должно быть представлено в
десятичной системе счисления.
2. Найдите сумму ряда. Полученное число
является значением числа в десятичной
системе счисления.
Примеры:
Переведем число 110012 в десятичную систему счисления.
1. Запишем число в развернутой форме:
110012 = 1 24+1 23 + 0 22 + 0 21 + 1 20.
2. Найдем сумму ряда:
24+23+0+0+20 = 16+8+4+1 = 2910.
Переведем число 16,48.
1. Запишем число в развернутой форме: 1 81+6 80+4 8-1
2. Найдем сумму: 8+6+0,5 = 14,510.
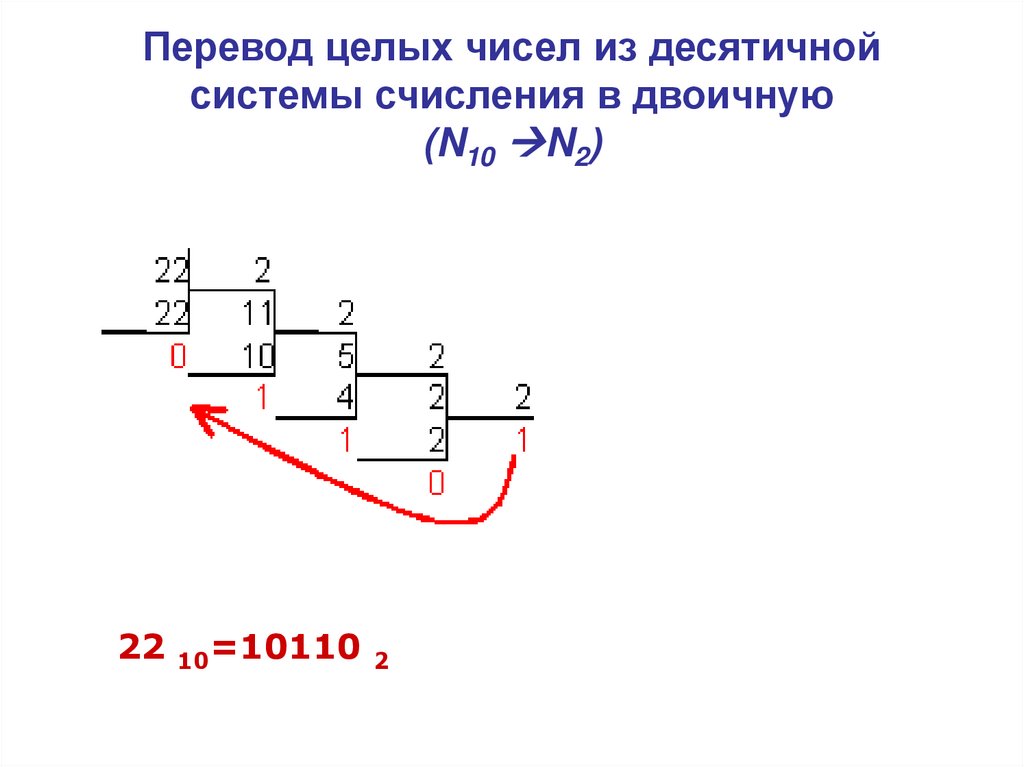
25. Перевод целых чисел из десятичной системы счисления в двоичную (N10 N2)
Перевод целых чисел из десятичнойсистемы счисления в двоичную
(N10 N2)
22
10=10110 2
26. Алгоритм перевода правильной десятичной дроби в двоичную:
• последовательно выполнять умножениедесятичной дроби и получаемых
дробных частей произведения на 2 до
тех пор, пока не получится нулевая
дробная часть (целое число) или не
будет достигнута требуемая точность;
• записать полученные целые части
произведения в прямой
последовательности.
27.
Система счисления – это способ записи чиселс помощью заданного набора специальных
знаков (цифр)
Системы счисления
непозиционные
вес цифры не зависит от
её позиции в числе
Единичная
Римская
(цифры I, V, X, L, C, D, M)
Древнеегипетская
Древнегреческая
Славянская
кириллическая
позиционные
вес каждой цифры изменяется
в зависимости от её положения
Двадцатеричная народов
племени Майя
Вавилонская
Древнекитайская
десятеричная
Двоичная
Десятичная
(0 1 2 3 4 5 6 7 8 9)

























 informatics
informatics








