Отношение между элементами одного множества

1.

Отношение между элементами
одного множества
Х = {1, 2}
Х = {1, 2}
Составим декартов квадрат
множества Х (Х2 или Х Х)
Х Х= {(1;1), (1; 2),

2.

Выделим пары с одинаковыми компонентами
в пределах пары, обозначим R.
R Х2
R = {х; у), х Х, у Х х = у }
R: «быть равным»
R={
.
.

3.

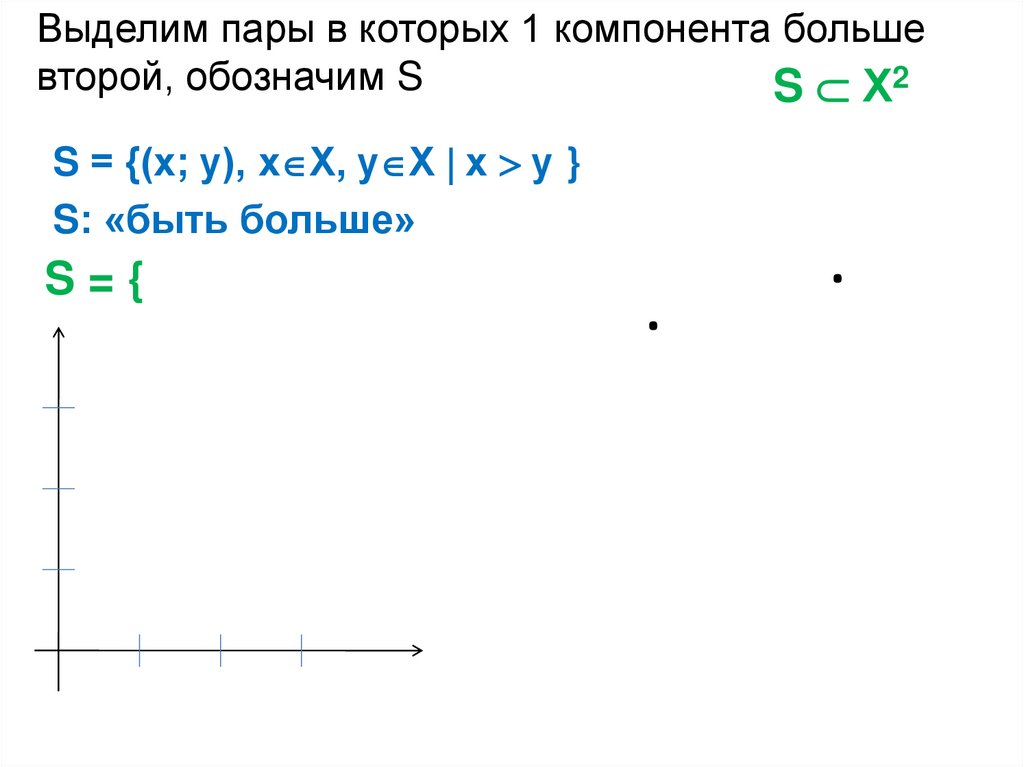
Выделим пары в которых 1 компонента больше
второй, обозначим S
S Х2
S = {(х; у), х Х, у Х х у }
S: «быть больше»
S={
.
.

4.

Любое подмножество R декартова квадрата Х2
называется отношением R на множестве Х.
Отношения в начальной школе
Положи 3 круга, а квадратов на 2 больше

5.

Отношения в начальной школе
Поезд, машина, велосипед и мотоцикл едут в
город Санкт – Петербург. Машина находится
дальше велосипеда, велосипед ближе поезда,
но дальше мотоцикла, а машина ближе
поезда. В каком порядке расположились по
близости к городу движущиеся тела?

6.

Отношения в начальной школе
На одной тарелке было в 3 раза больше
персиков, чем на другой. Когда с первой
тарелки взяли 8 персиков, а на другую
положили 5 персиков, то во второй тарелке
стало на 17 персиков меньше, чем в первой.
Сколько персиков было в каждой тарелке?

7.

Свойства отношений
Рефлексивность
Примеры:
Контрпримеры:

8.

Свойства отношений
Симметричность
Примеры:
Контрпримеры:

9.

Свойства отношений
Асимметричность
Примеры:
Контрпримеры:

10.

Свойства отношений
Антисимметричность
Примеры:
Контрпримеры:

11.

Свойства отношений
Транзитивность
Примеры:
Контрпримеры:

12.

Тренажер. Определите свойства отношений:
1.«Ученики х и у учатся в одной группе»
Р
С
аС
АС
Т
2.«Ученик х живет ближе к школе, чем ученик у»
Р
С
аС
АС
Т
3. «х похож на у»
Р
С
аС
АС
Т
4. «Быть перпендикулярным»
Р
С
аС
АС
Т

13.

5. «Дом х выше, чем дом у»
Р
С
аС
АС
Т
6. «Быть старше на 1 год»
Р
С
аС
АС
Т
7. «Прямая х параллельна прямой у»
Р
С
аС
АС
Т
АС
Т
8. «Пересекаться»
Р
С
аС