Similar presentations:
Частотные критерии устойчивости
1. Частотные критерии устойчивости
Лекция №111
2.
Принцип аргументаПусть имеется характеристический многочлен
замкнутой системы:
H ( P) a0 p n a1 p n 1 ... an 0
Используяn теорему Безу представим в виде:
H ( P) a0 * ( p pi )
i 1
Перейдем к частотному виду (заменим р на jω) и
найдем изменение аргумента и (jω) при
измененииn ω от нуля до бесконечности.
H ( j ) a 0 * ( j p i )
i 1
Найдем изменение аргумента:
n
arg H ( j ) arg( j pi )
i 1
2
3.
Рассмотрим расположения корней Н(р)=0 накомплексной плоскости:
Все корни Н(р)отрицательные вещественные:
j
Для Pi=- α будем иметь:
α+jω2
-α
jω2
φ
+
α+jω1
jω1
При
изменении
частоты
от
нуля
до
бесконечности результирующий вектор jω+ α
повернется в положительном направлении на
угол π, следовательно: arg( j )
3
4.
Рассмотрим расположения корней Н(р)=0 накомплексной плоскости:
Все корни Н(р)положительные вещественные:
j
Для Pi= α будем иметь:
jω2
α+jω2
φ
α
+
α+jω1
jω1
При
изменении
частоты
от
нуля
до
бесконечности результирующий вектор jω+ α
повернется в отрицательном направлении на
угол π, следовательно: arg( j )
4
5.
Среди корней имеется пара комплексносопряженных с отрицательной вещественной
j
j
частью:Pi;i+1=
jω+α-jB
B
α+jB
+
jω-α+jB
α-jB
-B
При изменении частоты от минус бесконечности
до бесконечности каждый из результирующих
векторов повернется против часовой стрелки на
угол π. Следовательно для одного корня
изменение аргумента будет: arg( j j )
5
6.
Среди корней имеется пара комплексносопряженных с положительной вещественной
частью:Pi;i+1= j
В этом случае для каждого корня изменение
аргумента:
arg( j j )
Данный случай рассмотреть самостоятельно.
6
7.
Один из корней равен jнулю: Pi;= 0.jω1
+
jω2
В данном случае не удается определить в каком
направлении
результирующий
вектор
охватывает начало координат. И следовательно
принцип аргумента не может быть использован
при наличии нулевого корня или пары чисто
мнимых корней.
7
8.
Пусть имеем характеристическое уравнениестепени n , причем оно содержит m правых
корней, следовательно n-m – левых, тогда
принцип аргумента может быть записан:
arg H ( j ) (n m) m( ) n m m
Очевидно, что при изменении частоты от
нуля до бесконечности будем иметь:
8
9.
Критерий МихайловаДанный
критерий
позволяет
судить
об
устойчивости
системы
по
заданному
характеристическому
уравнению
замкнутой
системы.
Пусть характеристическое уравнение замкнутой
системы имеет вид:
H ( р) a0 p a1 p
n
n 1
... an 0
Предположим,
что
система
с
заданным
характеристическим уравнением устойчива. Это
означает, что все корни этого уравнения
расположены
в
левой
полуплоскости,
и
следовательно m=0.
9
10.
1 формулировка критерия Михайлова имеетвид:
10
11.
Перейдем к частотному виду.На комплексной плоскости Н(jω) отображается
некоторым вектором, и конец этого вектора
при изменении частоты ω опишет некоторую
кривую,
которая
называется
кривой
Михайлова
Рассмотрим вид кривой Михайлова для
устойчивой системы, учитывая, что для
устойчивой
системы
выполняется
необходимое
условие
устойчивости,
следовательно an>0.
Каждый левый корень будет вносить аргумент
равный
, что соответствует охвату одного
2
11
квадрата в положительном направлении.
12.
2 формулировкаСАР будет устойчива, если кривая Михайлова
начинаясь
на
положительном
участке
вещественной
оси,
охватывает
последовательно
n
квадрантов
в
положительном направлении, где n – степень
характеристического уравнения Н(р)=0.
n
2
Im
n 1
Re
n 3
an
n
4
На рисунке приведен вид кривых Михайлова для
12
устойчивых систем 1-го – 4-го порядка.
13.
Критерий НайквистаДанный критерий позволяет дать суждения об
устойчивости замкнутой системы по
характеристикам разомкнутой системы.
Пусть передаточная функция разомкнутой
системы :
А( р)
W р ( р)
В( р)
А(р) – многочлен степени m
В(р) – многочлен степени n, где m ≤ n.
13
14.
Введемв
рассмотрение
функцию F(p):
F(р)=1+Wp(р)=
вспомогательную
А( р) H ( р)
1
В( р) B( р)
Где Н(р)=A(p)+ B(p) – характеристический
многочлен замкнутой системы;
В(р) – характеристический многочлен
разомкнутой системы;
Перейдем к частотному виду:
F ( j )
H ( j )
B( j )
14
15.
Найдем изменение аргумента вспомогательнойфункции при изменении частоты от 0 до
бесконечности.
arg F ( j ) arg H ( j ) arg B( j )
0
0
0
Из данного выражения следует, что изменение
аргумента вспомогательной функции зависит от
расположения корней как замкнутой так и
разомкнутой систем.
15
16.
Исходя из этого рассмотрим критерийНайквиста для следующих случаев
расположения корней в разомкнутой
системе:
1.
Все
корни
В(р)=0
левые,
следовательно САР в разомкнутом
состоянии устойчива.
2. Среди корней В(р)=0 имеется хотя
бы один правый корень, т.е САР в
разомкнутом состоянии неустойчива.
3. В(р)=0 имеет нулевые корни, и
система будет находиться на границе16
устойчивости.
17.
Критерий Найквиста для систем устойчивых вразомкнутом состоянии
Характеристическое уравнение В(р)=0 имеет все
корни, расположенные в левой полуплоскости
плоскости корней, следовательно:
arg В( j ) n * 2
0
Нас интересует устойчивость САР в замкнутом
состоянии. Предположим, что она устойчива в
замкнутом состоянии, это означает, что все корни
Н(р)=0 будут левые, а следовательно:
arg H ( j ) n *
0
2
Подставим полученные значение в исходное
равенство, тогда будем иметь :
arg F ( j ) n * n * 0
17
0
2
2
18.
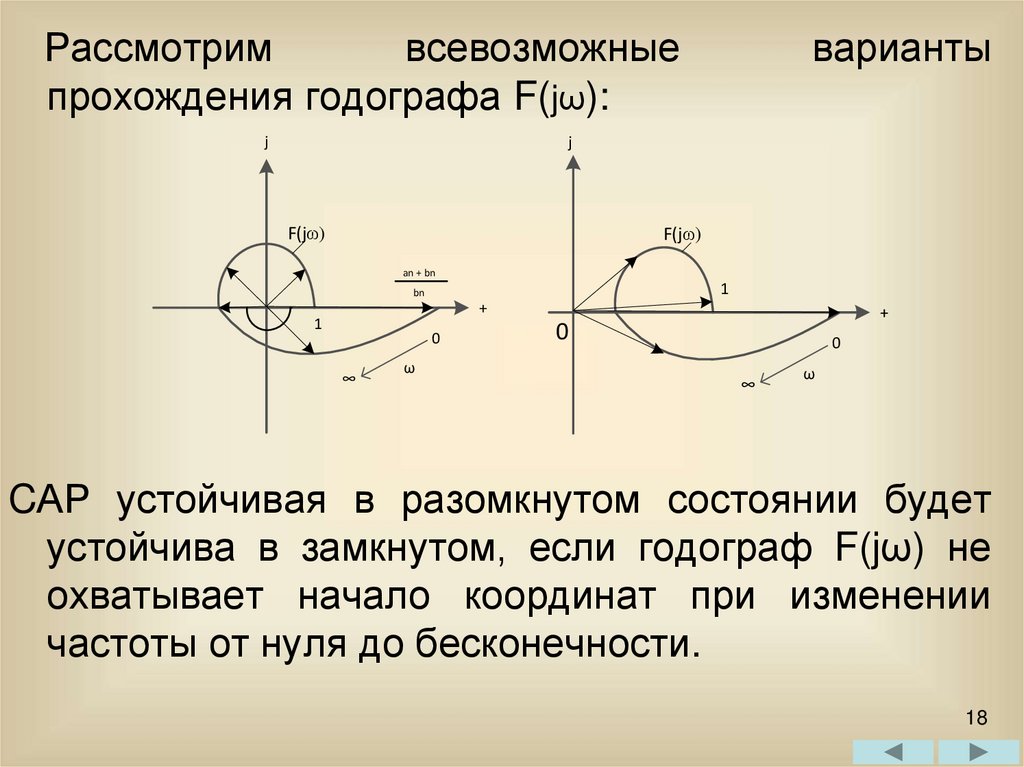
Рассмотримвсевозможные
прохождения годографа F(jω):
j
варианты
j
F(jω)
F(jω)
an + bn
1
bn
+
1
0
∞
+
0
0
ω
∞
ω
CАР устойчивая в разомкнутом состоянии будет
устойчива в замкнутом, если годограф F(jω) не
охватывает начало координат при изменении
частоты от нуля до бесконечности.
18
19.
F(p)=1+Wp(p); Wp(p)=F(p)-1; Wp(jω)=F(jω)-1т.е. годограф Wр(jω) может быть получен из
годографа F(jω) путем сдвига его на
единицу по вещественной оси.
19
20.
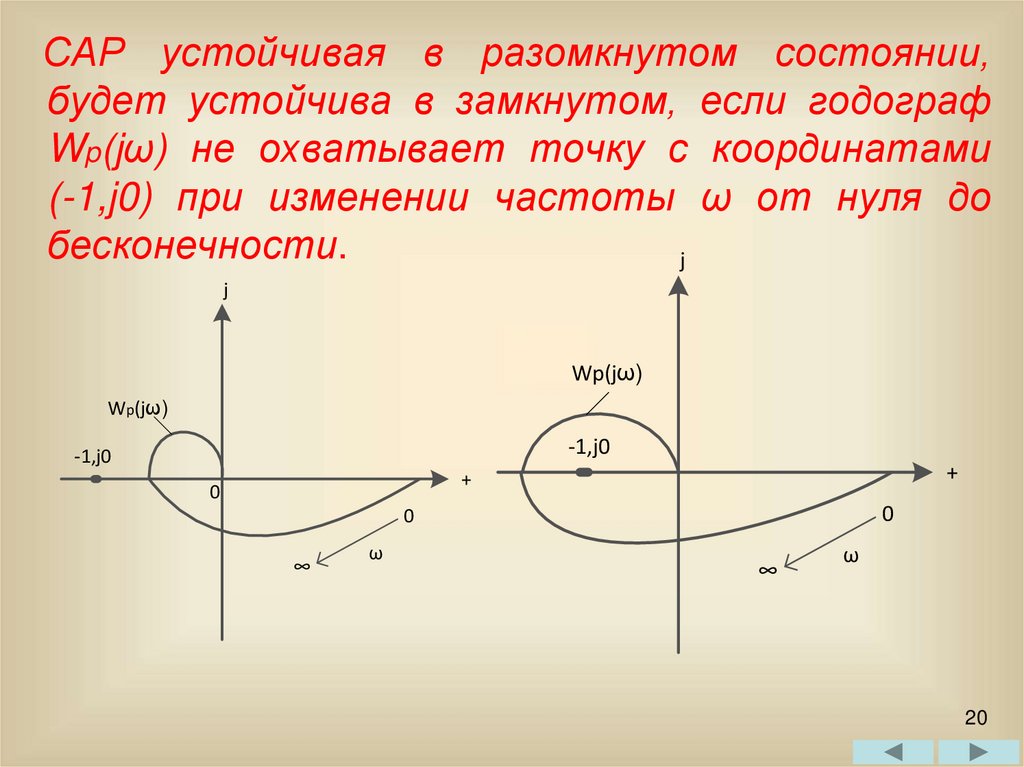
САР устойчивая в разомкнутом состоянии,будет устойчива в замкнутом, если годограф
Wp(jω) не охватывает точку с координатами
(-1,j0) при изменении частоты ω от нуля до
бесконечности.
j
j
Wp(jω)
Wp(jω)
-1,j0
-1,j0
+
+
0
0
0
∞
ω
∞
ω
20


















 electronics
electronics








