Similar presentations:
Теорема Пифагора
1.
2.
Древнегреческийфилософ и
математик
(580 - 500 г. до н.э.)
3. c2 = a2 + b2
2c
=
2
a
+
2
b
В прямоугольном
треугольнике квадрат
гипотенузы равен сумме
квадратов катетов.
Площадь квадрата, построенного на
гипотенузе прямоугольного треугольника,
равна сумме площадей квадратов,
построенных на его катетах.
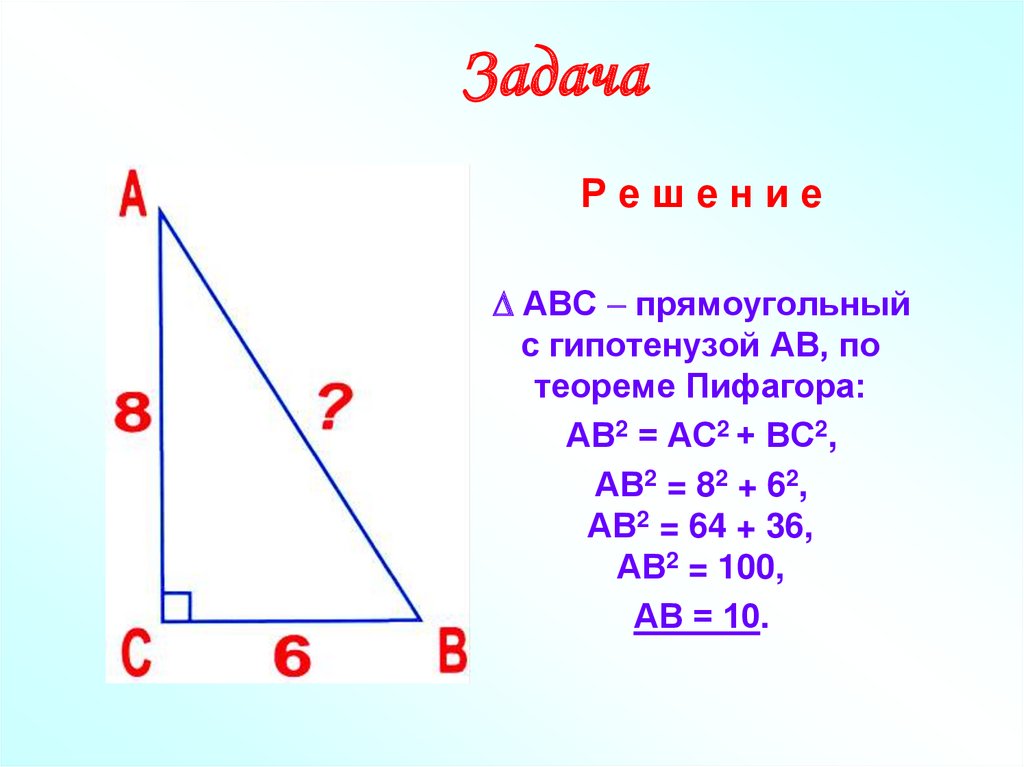
4. Задача
РешениеАВС прямоугольный
с гипотенузой АВ, по
теореме Пифагора:
АВ2 = АС2 + ВС2,
АВ2 = 82 + 62,
АВ2 = 64 + 36,
АВ2 = 100,
АВ = 10.
5. Задача
РешениеDCE прямоугольный
с гипотенузой DE, по
теореме Пифагора:
DE2 = DС2 + CE2,
DC2 = DE2 CE2,
DC2 = 52 32,
DC2 = 25 9,
DC2 = 16,
DC = 4.
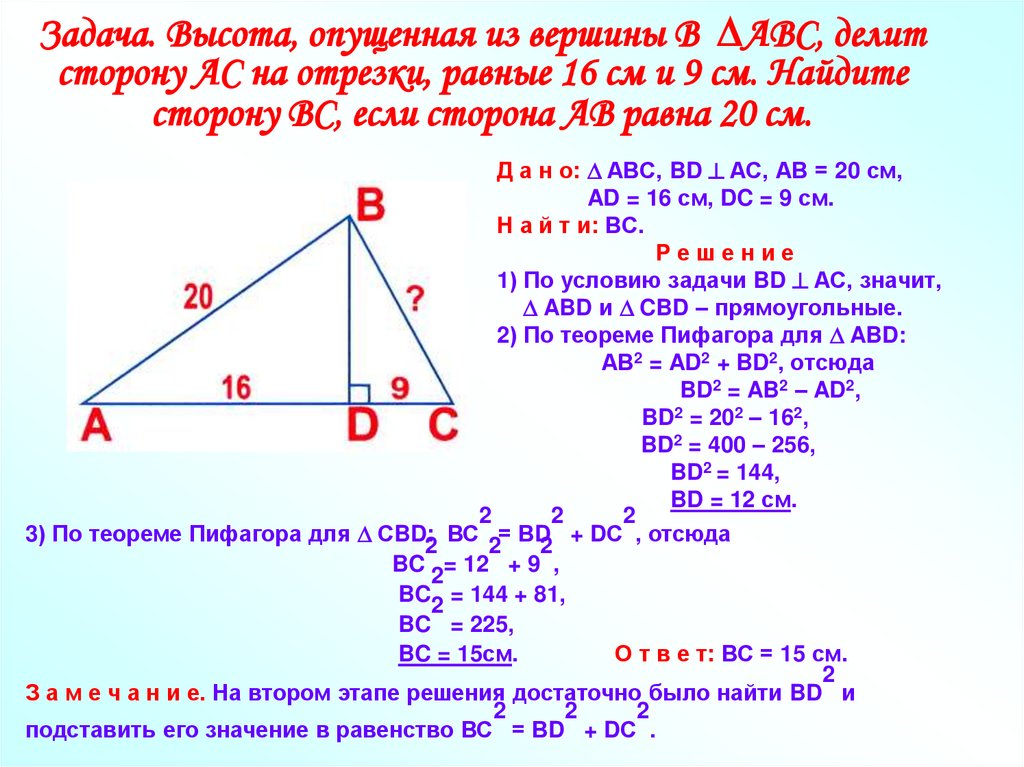
6. Задача. Высота, опущенная из вершины В АВС, делит сторону АС на отрезки, равные 16 см и 9 см. Найдите сторону ВС, если сторона
Задача. Высота, опущенная из вершины В АВС, делитсторону АС на отрезки, равные 16 см и 9 см. Найдите
сторону ВС, если сторона АВ равна 20 см.
Д а н о: АВС, BD АС, АВ = 20 см,
AD = 16 см, DC = 9 см.
Н а й т и: ВС.
Решение
1) По условию задачи BD АС, значит,
ABD и CBD – прямоугольные.
2) По теореме Пифагора для ABD:
АВ2 = AD2 + BD2, отсюда
BD2 = AB2 – AD2,
BD2 = 202 – 162,
BD2 = 400 – 256,
BD2 = 144,
BD = 12 см.
2
2
2
3) По теореме Пифагора для СBD:2 ВС 2= ВD2 + DС , отсюда
BC 2= 12 + 9 ,
BC2 = 144 + 81,
BC = 225,
BC = 15см.
О т в е т: ВС = 15 см.
2
З а м е ч а н и е. На втором этапе решения достаточно было найти BD и
2
2
2
подставить его значение в равенство ВС = ВD + DС .
7.
Теорема, обратная теореме Пифагора.Если квадрат одной стороны треугольника равен
сумме квадратов двух других сторон, то
треугольник прямоугольный.
Существует бесчисленное множество целых положительных
чисел, удовлетворяющих соотношению
2
2
2
с =а +b .
Они называются п и ф а г о р о в ы м и
числами
8.
Вот несколько троек пифагоровых чисел.2
2
3 +4 =5
2
2
6 + 8 = 10
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
5 + 12 = 13
7 + 24 = 25
9 + 40 = 41
2
11 + 60 = 61
13 + 84 = 85
2
2
2
9 + 12 = 15
2
2
2
12 + 16 = 20
2
Треугольник со сторонами 3, 4 и 5 часто
называют египетским треугольником
т. к. он был известен еще древним египтянам.
9.
Для прямоугольных треугольников составить равенства,выражающие зависимость между сторонами прямоугольного
треугольника, по теореме Пифагора.
АВСD – ромб
В
АВ2=АО2
+
ВС2 = ВО2 + ОС2
ОВ2
А
О
С
DC2 = DO2 + OC2
АD2 = DO2 + OA2
D
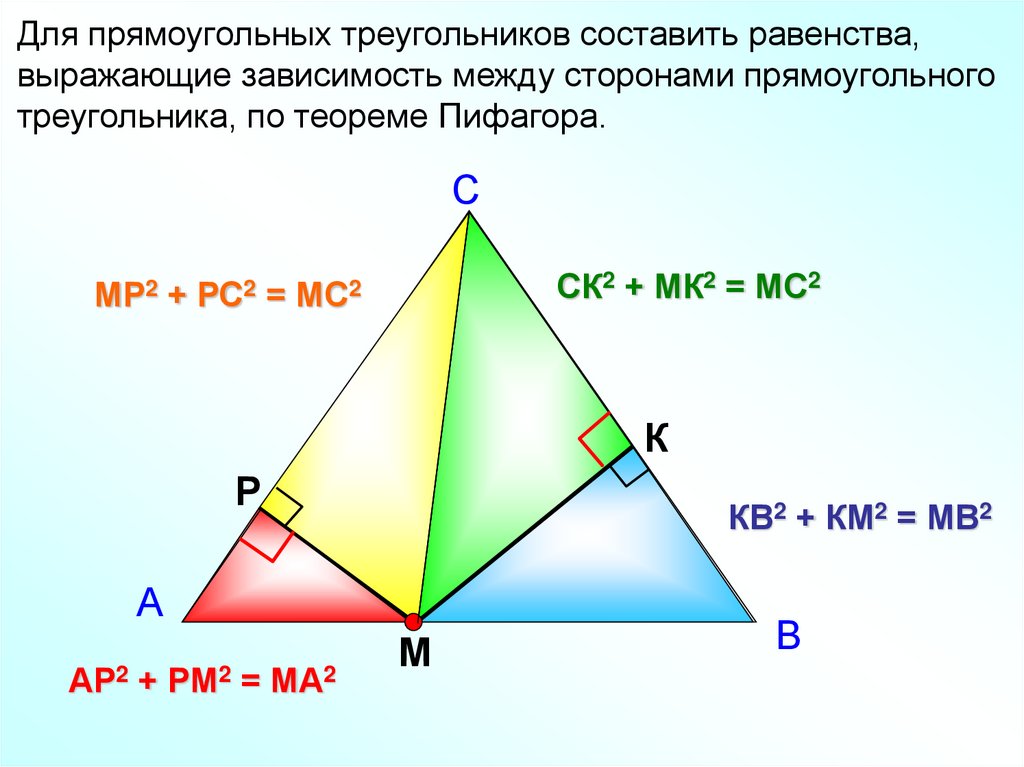
10.
Для прямоугольных треугольников составить равенства,выражающие зависимость между сторонами прямоугольного
треугольника, по теореме Пифагора.
С
МР2
+
РС2
=
СК2 + МК2 = МС2
МС2
К
Р
КВ2 + КМ2 = МВ2
А
АР2 + РМ2 = МА2
М
В
11.
Для прямоугольного треугольника составить равенства,выражающие зависимость между сторонами прямоугольного
треугольника.
С
Выразить гипотенузу АВ
АВ2 = АС2 + ВС2
АВ АС СВ
2
А
2
В
Выразить катет АС
Выразить катет ВС
АС2 = АВ2 –СВ2
АС АВ СВ
2
ВС2 = АВ2 –СА2
2
ВС АВ2 СА2
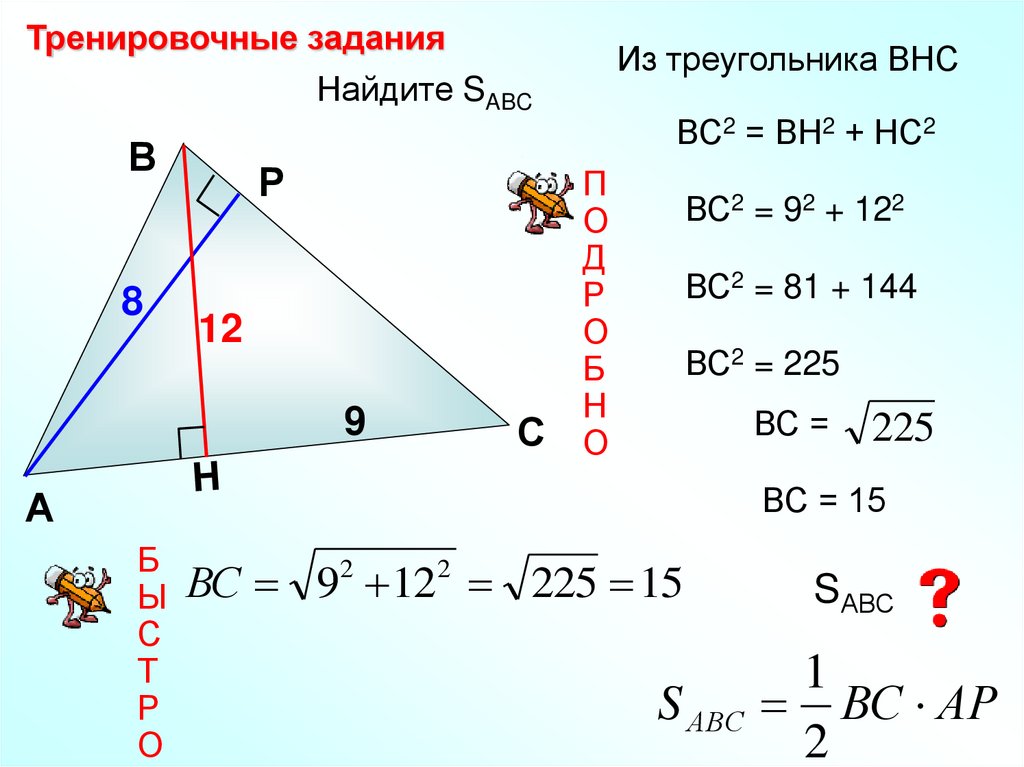
12.
Тренировочные заданияНайдите SABC
В
8
Р
12
9
С
Из треугольника ВНС
ВС2 = ВН2 + НС2
П
О
Д
Р
О
Б
Н
О
ВС2 = 92 + 122
ВС2 = 81 + 144
ВС2 = 225
ВС =
225
ВС = 15
А
Б
Ы
С
Т
Р
О
ВС 92 122 225 15
S АВС
SАВС
1
ВС АР
2








 mathematics
mathematics








