Равнобедренный треугольник

1. Равнобедренный треугольник

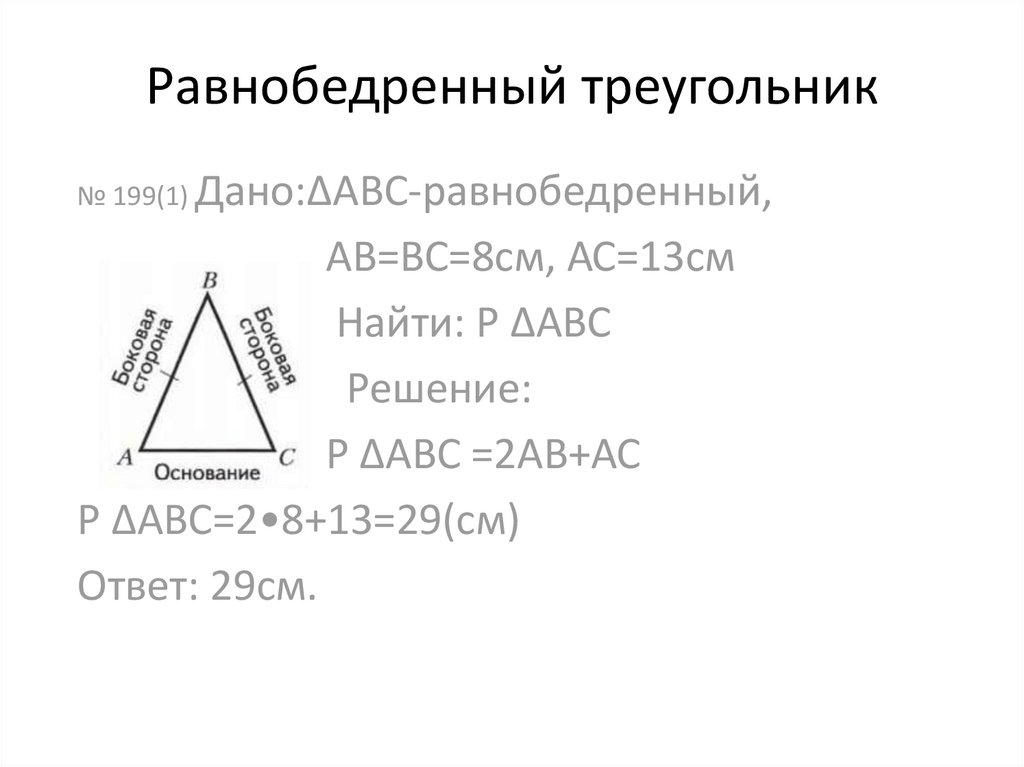
№ 199(1) Дано:ΔАВС-равнобедренный,
АВ=ВС=8см, АС=13см
Найти: Р ΔАВС
Решение:
Р ΔАВС =2АВ+АС
Р ΔАВС=2•8+13=29(см)
Ответ: 29см.

2. Равнобедренный треугольник

№ 199(2) Дано:ΔАВС-равнобедренный,
АВ=ВС, Р ΔАВС =39см,
АС=15 см
Найти: АВ, ВС
Решение:
Р ΔАВС =2АВ+АС
АВ=ВС= (Р ΔАВС –АС):2=(39-15):2=
24:2=12(см)
Ответ: 12см, 12см.

3. Равнобедренный треугольник

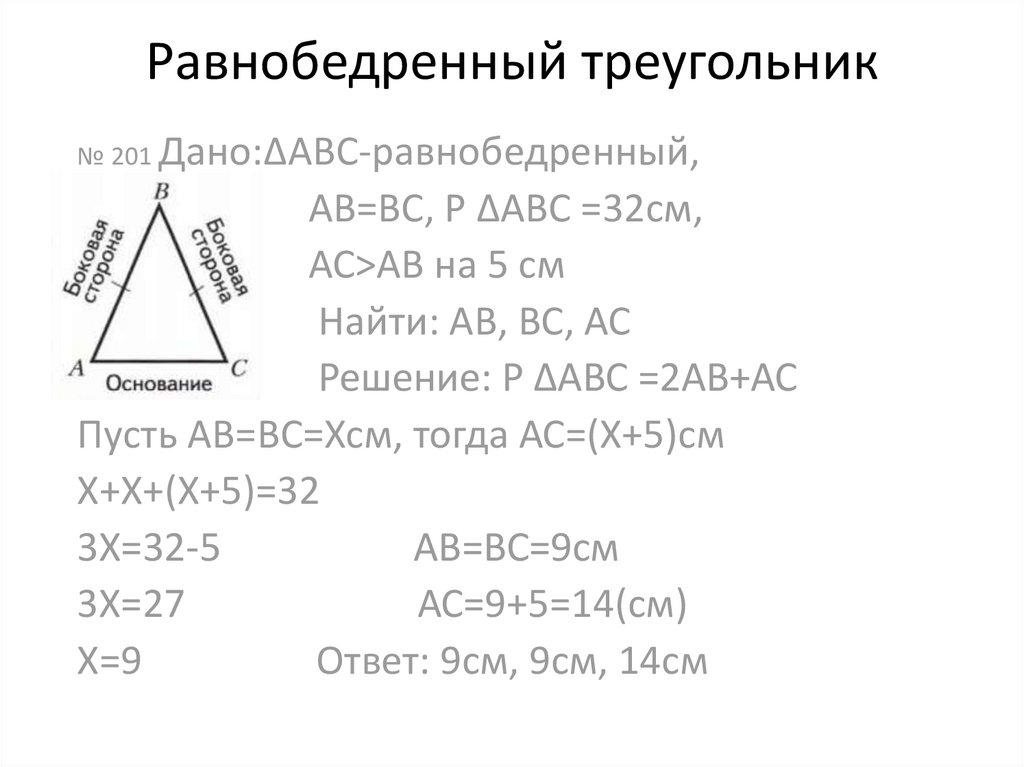
№ 201 Дано:ΔАВС-равнобедренный,
АВ=ВС, Р ΔАВС =32см,
АС>АВ на 5 см
Найти: АВ, ВС, АС
Решение: Р ΔАВС =2АВ+АС
Пусть АВ=ВС=Хсм, тогда АС=(Х+5)см
Х+Х+(Х+5)=32
3Х=32-5
АВ=ВС=9см
3Х=27
АС=9+5=14(см)
Х=9
Ответ: 9см, 9см, 14см

4. Равнобедренный треугольник

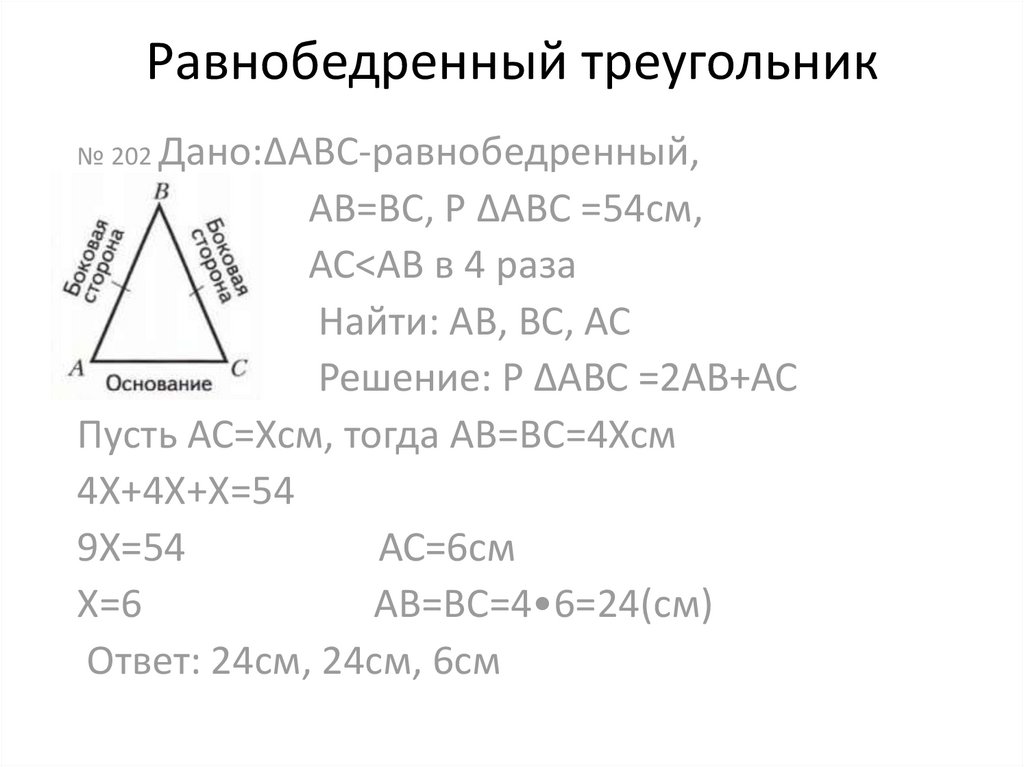
№ 202 Дано:ΔАВС-равнобедренный,
АВ=ВС, Р ΔАВС =54см,
АС<АВ в 4 раза
Найти: АВ, ВС, АС
Решение: Р ΔАВС =2АВ+АС
Пусть АС=Хсм, тогда АВ=ВС=4Хсм
4Х+4Х+Х=54
9Х=54
АС=6см
Х=6
АВ=ВС=4•6=24(см)
Ответ: 24см, 24см, 6см

5.

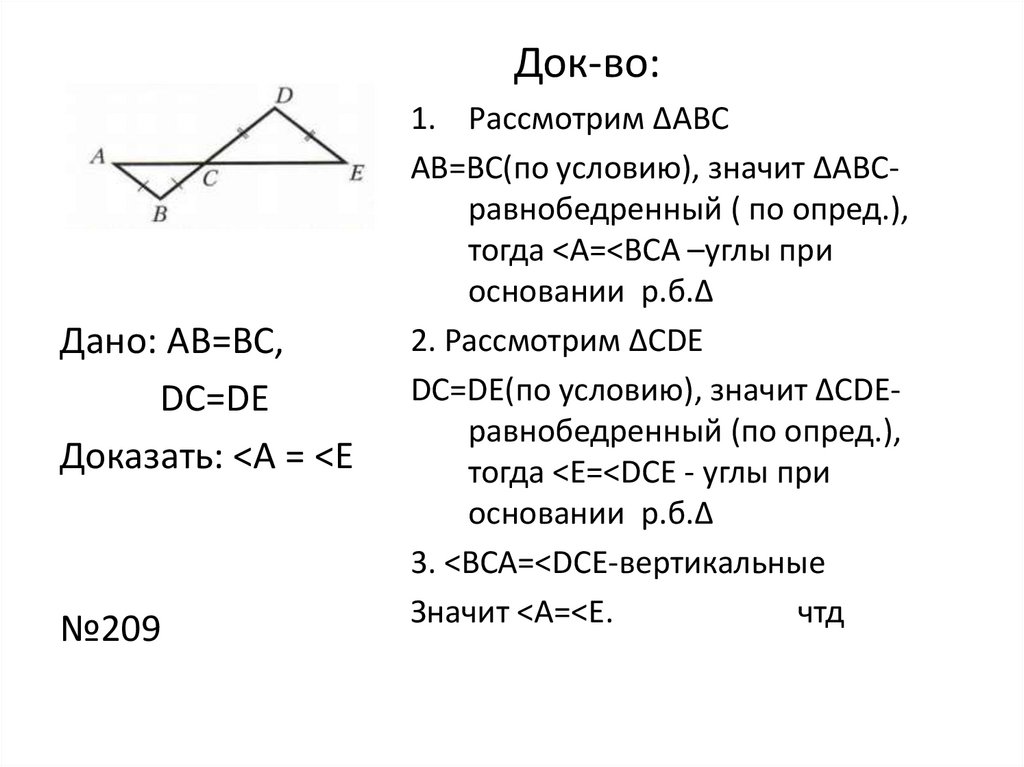
Док-во:
Дано: АВ=ВС,
DC=DE
Доказать: <А = <Е
№209
1. Рассмотрим ΔАВС
АВ=ВС(по условию), значит ΔАВСравнобедренный ( по опред.),
тогда <А=<ВСА –углы при
основании р.б.Δ
2. Рассмотрим ΔCDE
DC=DE(по условию), значит ΔCDEравнобедренный (по опред.),
тогда <Е=<DCE - углы при
основании р.б.Δ
3. <ВСА=<DCE-вертикальные
Значит <А=<Е.
чтд

6.

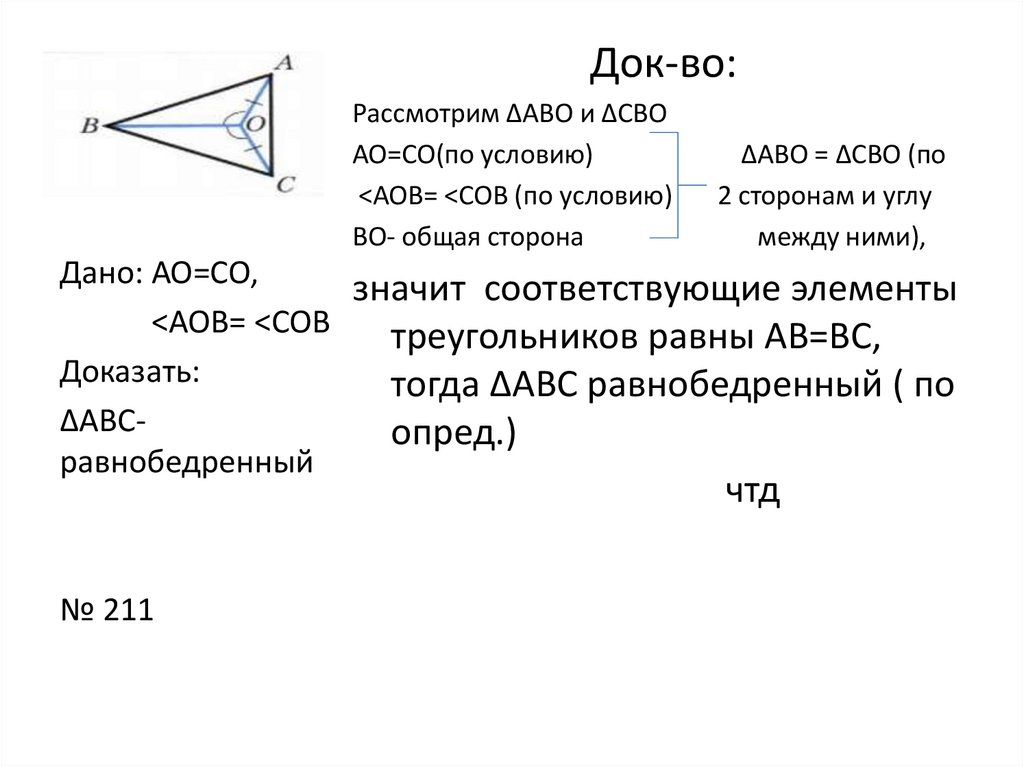
Док-во:
Рассмотрим ΔАВО и ΔСВО
АО=СО(по условию)
<АОВ= <СОВ (по условию)
ВО- общая сторона
ΔАВО = ΔСВО (по
2 сторонам и углу
между ними),
Дано: АО=СО,
значит соответствующие элементы
<АОВ= <СОВ
треугольников равны АВ=ВС,
Доказать:
тогда ΔАВС равнобедренный ( по
ΔАВСопред.)
равнобедренный
чтд
№ 211