Элементы механики сплошных сред

1.

Курс общей физики НИЯУ МИФИ
Основы механики
Лекция
Элементы механики сплошных сред
Лектор: Доцент НИЯУ МИФИ, к.ф.-м.н.,
Ольчак Андрей Станиславович

2.

Механика жидкостей и газов
1. Механика материальной точки
2. Механика твердого тела
3. Механика жидкостей и газов

3. Механика жидкостей и газов

Что мы знаем из школьного курса физики?
1) На тело, погруженное в газ или жидкость, действует сила Архимеда,
направленная вверх и равная численно весу вытесненной телом жидкости
или газа:
Fарх = ρжgVтела
2) На поверхность тел, погруженных в газ или жидкость, действует сила
гидродинамического давления, пропорциональная площади поверхности
и перпендикулярная ей.
3) Давление атмосферы у поверхности Земли равно Ратм =~ 105 Па
4) На глубине Н под поверхностью жидкости ее давление равно:
Р = ρжgН
5) На тело, движущееся в жидкости или газе, действует сила
сопротивления, направленная против скорости тела (если тело имеет
простую геометрическую форму) и тем большая, чем больше скорость.
Fсопр ~ v или v2

4. Примеры задач

На тело, погруженное в газ или жидкость, действует сила Архимеда,
направленная вверх и равная численно весу вытесненной телом жидкости
или газа:
Fарх = ρжgVтела
1. Два тела равного объема уравновешены на весах. Как изменится
положение рычага весов, если поместить грузы в воду?
ОТВЕТ: Никак
2. …а если поместить в воду только один из грузов?
ОТВЕТ: Другой груз начнет перевешивать
3. …а если объемы тел разные?
Станет перевешивать то, что имеет меньший объем. :

5.

Примеры задач
2) На поверхность тел, погруженных в газ или жидкость, действует сила
гидродинамического давления, пропорциональная площади поверхности
и перпендикулярная ей.
3) Давление атмосферы у поверхности Земли равно Ратм =~ 105 Па
4) На глубине Н под поверхностью жидкости ее давление равно:
Р = ρжgН
ПРИМЕРЫ:
1. «Магдебургские полушария»:
Какую силу надо приложить,
чтобы их разъединить?
F = SРатм , где S - площадь стыка
полушарий
2. Гидравлический пресс:
Уравновешивающие силы
F1/F2 = S1/S2

6. Механика жидкости

Основные понятия и определения
v
dV
1) Частица жидкости - малый объем ее dV,
выделенный для рассмотрения. Аналог
материальной точки. Малый объем - по
сравнению с областью течения, но большой по
сравнению с межмолекулярными
расстояниями.
2) Для каждой частицы жидкости можно указать
ее вектор скорости как функцию времени.
3) Совокупность векторов скорости для всех точек
течения образует поле вектора скорости.
4) Если вектор скорости в каждой точке течения остается постоянным течение называют стационарным.
5) Несжимаемая жидкость - такая жидкость, плотность которой ρ во
всех точках течения постоянна и одинакова.

7.

Механика несжимаемой жидкости
Основные понятия и определения
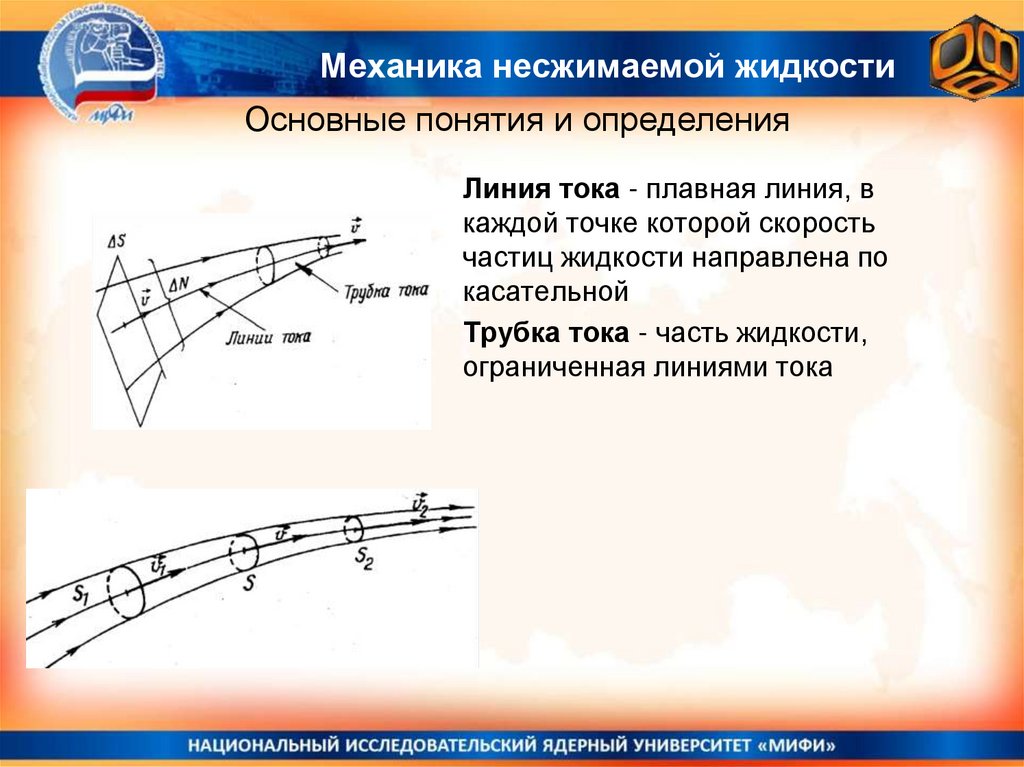
Линия тока - плавная линия, в
каждой точке которой скорость
частиц жидкости направлена по
касательной
Трубка тока - часть жидкости,
ограниченная линиями тока

8.

Механика несжимаемой жидкости
Уравнение неразрывности струи
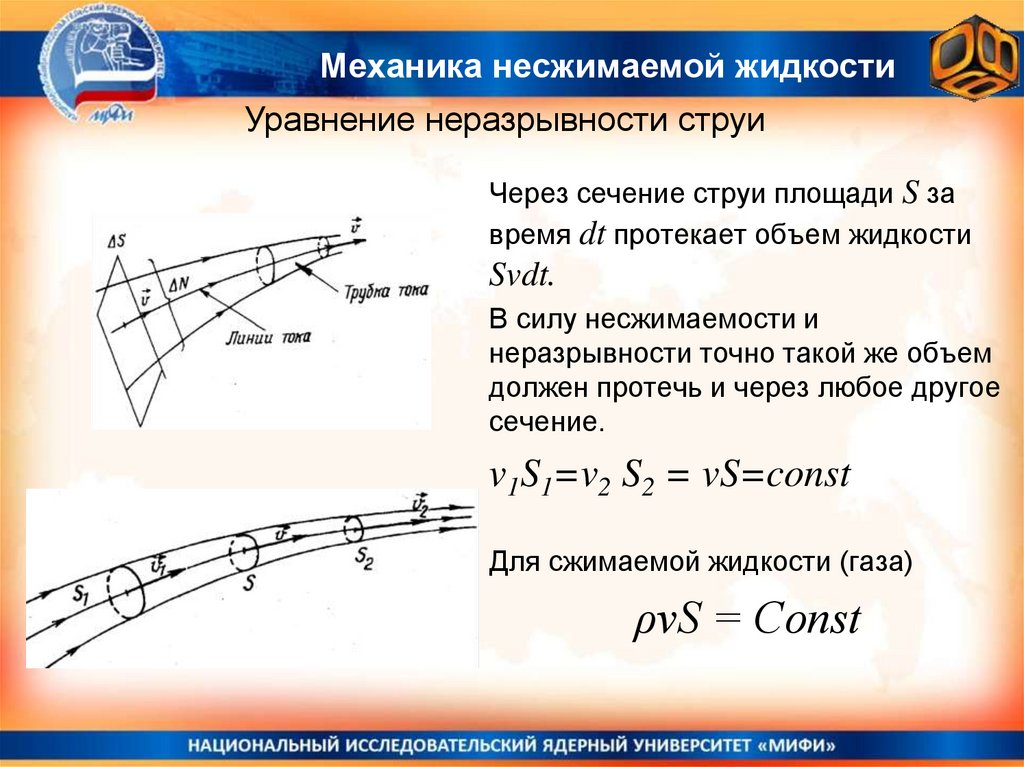
Через сечение струи площади S за
время dt протекает объем жидкости
Svdt.
В силу несжимаемости и
неразрывности точно такой же объем
должен протечь и через любое другое
сечение.
v1S1=v2 S2 = vS=const
Для сжимаемой жидкости (газа)
ρvS = Const

9.

Механика несжимаемой жидкости
Поток жидкости
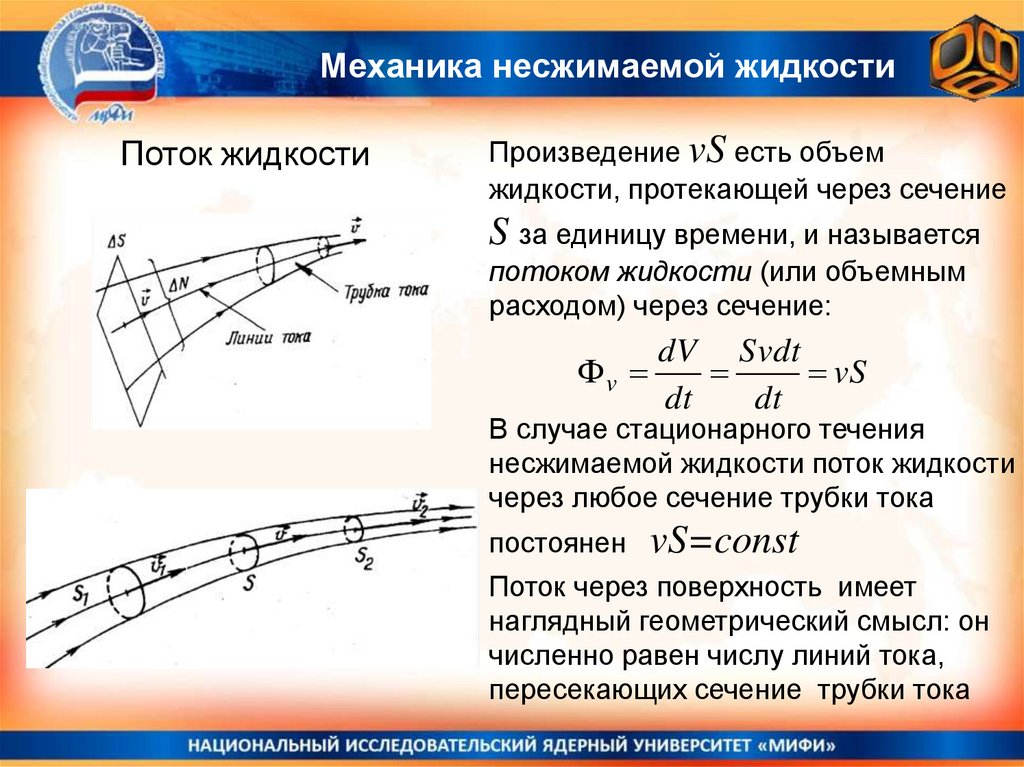
Произведение vS есть объем
жидкости, протекающей через сечение
S за единицу времени, и называется
потоком жидкости (или объемным
расходом) через сечение:
dV Svdt
v
vS
dt
dt
В случае стационарного течения
несжимаемой жидкости поток жидкости
через любое сечение трубки тока
постоянен
vS=const
Поток через поверхность имеет
наглядный геометрический смысл: он
численно равен числу линий тока,
пересекающих сечение трубки тока

10.

Ламинарность и турбулентность
Ламинарное течение – линии
тока не пересекаются.
Ламинарное течение может быть
стабильным и стационарным.
Турбулентное течение: линии тока
завихрятся, обрываются,
пересекаются… Течение
нестабильное, нестационарное.
пульсирующее.
Большинство течений в природе турбулентны

11.

Гидродинамическое подобие
Характер течения определяется т.н. числом Рейнольдсa Re
= ρvr/η
r
- характерный геометрический размер течения или обтекаемого тела
(диаметр трубы, радиус обтекаемого шарика, толщина крыла и т.п.
η - вязкость среды (параметр, характеризующий внутреннее трение
в среде (в газе или жидкости) и сопротивление, которое оказывает
среда движущимся в ней телам
Re < 1 - течение ламинарное, сопротивление среды Fres ~ v
Re >> 1 - течение турбулентное, сопротивление среды Fres ~ v2
Течения со сходными значениями Re – гидродинамически подобны.

12.

Ламинарное обтекание сферы
F = - 6πηrv
Формула Стокса для силы сопротивления
движению шарообразного тела радиуса r
в жидкости с динамической вязкостью
η
ПРИМЕР: скорость устойчиворавномерного падения шарика в
= gρ(4/3)πr3 = 6πηrv
v = 2gρr2/9η
жидкости: mg
А еще: для ламинарного течения можно получить достаточно простое
дифференциальное уравнение, которым оно описывается

13.

Уравнения Навье - Стокса
dv
Fтр S
dz

14.

Уравнения Навье - Стокса
mw Fi
i
dv
dV
pdV v dV gdV
dt
dv
p v g
dt
ПРИМЕР: с помощью УНС можно, например, рассчитать скорость течения
жидкости c вязкостью η в трубе длины l и радиуса R:
v = R2∆P/4ηl ,
где ∆P - разность давлений на концах трубы

15.

Уравнения Навье - Стокса
уравнение Навье
Основное
dv
Стокса для несжимаемой
p v g -жидкости
dt
Уравнение
div v =δvx/δx + δvy/δy+ δvz/δz = 0 неразрывности
v = 0 например, на границах области тока - граничное условие
v(r,t=0) = v0(r) - начальное условие
ПРИМЕР: с помощью УНС можно, например, рассчитать скорость
течения жидкости c вязкостью η в трубе длины l и радиуса R:
v = R2∆P/4ηl ,
где ∆P - разность давлений на концах трубы

16.

Уравнения идеальной жидкости
Жидкость, в которой отсутствуют
силы трения, называют идеальной.
Для идеальной жидкости
справедливо уравнение Эйлера
dv
P g .
dt
Умножим уравнение Эйлера скалярно на dr = vdt:
d(ρv2/2) = d(ρ(g,r)) - dp ; g ge z
Интегрируя, получаем уравнение Бернулли:
ρv2/2 +р+ρgz = B,
где В - постоянная Бернулли
Вдоль трубки тока величина v 2
2
gz p
остается постоянной

17.

Истечение жидкости из отверстия
Задача: как быстро выльется вода из сосуда
высоты h с основанием S через малое
отверстие у дна площади s.
S
РЕШЕНИЕ: Давление в верхнем (S) и нижнем (s)
сечениях трубки тока одинаково и равно
атмосферному. Следовательно:
v02 v 2
gh
2
2
v 0 S vs
dh
v0
dt
v
s
- скорость опускания
свободной поверхности
- скорость истечения из отверстия
v = (2gh/(1 - s2/S2))1/2 => v
dh s
S
v0
2 gh =>
dt S
s 2g
H
0
2 gh
- формула Торричелли
S
dt =>
s
h 0
dh
2H
g

18.

Истечение жидкости
Задача о пульверизаторе. .
Давление у входа в трубку
*внизу) – Р0. Скорость потока
газа над трубкой - v. На какую
максимальную высоту
устройство может поднять воду ?
Над трубкой статическое
давление понизится на величину
давления – ρвоздv2/2, что
позволяет скомпенсировать
давление столба воды ρводgh:
ОТВЕТ:
gh = ρвоздv2/2gρвод

19.

Силы упругости. Модуль Юнга
Всякое реальное тело под действием приложенных к нему сил
изменяет свои размеры и форму, т.е. деформируется. Если после
прекращения действия сил тело принимает первоначальные размеры
и форму, деформация называется упругой. Сила упругости
определяется законом Гука. Fупр = - kΔX
Для твердых тел (стержней) закон Гука принимает форму:
ES
k
l0
Здесь коэффициент Е [н/м2] называется модулем Юнга и характеризует
прочность твердых тел. Для металлов он составляет 109 - 1011 н/м2

20.

Задание на пятницу, 11.12
Савельев. 1.338, 339, 341, 343, 346
Иродов. 1.368, 370,372, 373, 384

21.

Курс общей физики НИЯУ МИФИ
Спасибо за внимание!

22.

Курс общей физики НИЯУ МИФИ
Спасибо за внимание!
Удачи на экзаменах!