Показатели качества регулирования. Точность регулирования

1. Показатели качества регулирования. Точность регулирования.

Лекция №14
1

2.

Качество САР
Устойчивость САР является необходимым
условием работы реальных технических
систем.
Для оценки качества функционирования
используются характеристики:
1) Точность регулирования;
2) Время регулирования;
3) Перерегулирование.
2

3.

Точность регулирования САР определяется по
величине
ошибки
регулирования
в
установившимся режиме.
В зависимости от входного воздействия ошибки
регулирования подразделяются:
Статические;
Кинетические;
Динамические.
3

4.

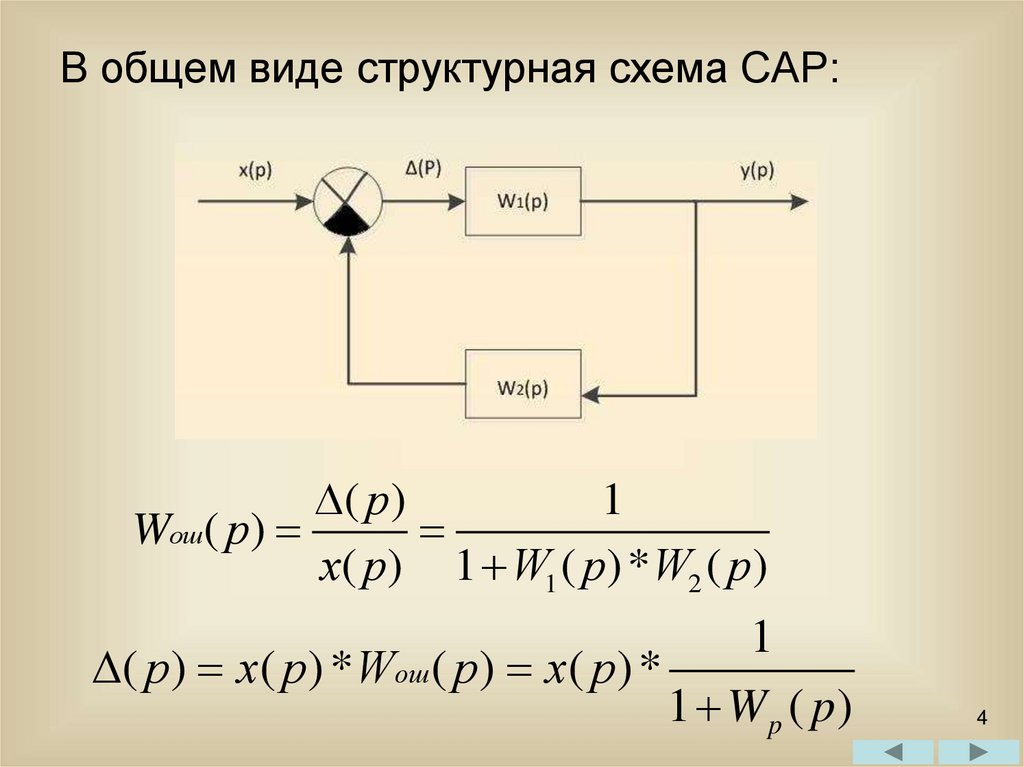
В общем виде структурная схема САР:
( р )
1
Wош( р)
х( р) 1 W1 ( p) *W2 ( p)
1
( р) x( p) * Wош( p) x( p) *
1 Wp ( p)
4

5.

Статическая ошибка
Ошибка регулирования в установившимся
режиме, при подаче на вход ступенчатого
воздействия называется статической ошибкой
регулирования.
Для нахождения этой ошибки используем
свойство о конечном значении функции
оригинала.
(t ) t lim p * ( p)
p 0
А
1
1
ст (t ) t lim p * *
A * limWош( p) A lim
p 0
p 0
p 0 1 Wp( p)
р 1 Wp( p)
5

6.

Найдем статическую ошибку для статической
системы регулирования.
Пусть Wр ( Р) 1 ;
1 рТ
1 рТ
Тогда Wош( Р) рТ ( K 1) ;
р
1 pT
A
cт A * lim
p 0 pT (1 К )
К р 1
р
Вывод: в статической системе величина ошибки
регулирования зависит от величины входного
воздействия
и
коэффициента
передачи
разомкнутой системы. Чем больше Кр, тем
меньше частотная ошибка регулирования.
6

7.

Найдем статическую ошибку для астатической
системы регулирования.
Пусть Wp K p
p
По аналогии с предыдущем случаем будем иметь:
1
p
Wош ( p )
Kp
p Kp
1
p
И величина статической ошибки будет равна:
p
cт A * lim
0
p 0 p K
p
Вывод: в астатической системе
ошибка тождественно равна нулю.
статическая
7

8.

Кинетическая ошибка
Кинетической ошибкой называется ошибка
регулирования в установившимся режиме при
подаче на вход линейно нарастающего
возрастающего входного транзистора.
X(t)
0
x(t ) A * t *1 (t )
t
A
x( p) 2
p
кин (t )
t lim * p *
p 0
A * lim
p 0
A
1
*
2
p 1 Wp ( p)
1
1
1
* Wош( p ) Alim *
p
p 0 p 1 W p ( p )
8

9.

Найдем кинетическую ошибку для статической
систем и астатической систем первого порядка.
По аналогии с определением статической
ошибки для статической системы будем иметь:
1
1 pT
кин A * lim *
p 0 p
pT ( K p 1)
В статической САР кинетическая ошибка
регулирования
равна
бесконечности,
следовательно статические системы не
работоспособны при нарастающем линейно
нарастающем входном воздействии
9

10.

Для астатической системы:
1
p
A
кин A * lim *
p 0 p
p Kp Kp
В астатической системе кинетическая
ошибка конечна и зависит от скорости
нарастания входного воздействия, т.е. от А.
Величина Кр в данном случае называется
добротностью САР.
10

11.

Динамическая ошибка
Динамическая ошибка определяется при
подаче на вход гармонического сигнала
заданной частоты ωк.
x(t ) A * sin k t *1 (t )
Перейдем в частотную область:
1
дин( j ) A * lim
p 0 1 W ( j )
p
При нахождении динамической ошибки ищут ее
максимальное значение, причем ошибку ищут в
полосе частот, где W p ( j )
значительно
больше 1, тогда:
A
Wдин max
11
W p ( j )

12.

В соответствии с
задается амплитуда и
техническим
дин max( . k )
A
W p ( j )
дин max
заданием
Амплитуду динамической ошибки находят по
логарифмической характеристике.
-20 дб/дек
20lg|Wp(jωk)|
-40 дб/дек
-60 дб/дек
Для того что бы динамическая ошибка была
меньше заданной, нужно что бы построенная
ЛАЧХ была выше точки или проходила через нее12

13.

Прямые показатели качества регулирования
Показатели качества, найденные по кривой
переходного
процесса
называют
прямые
показатели качества.
В общем виде для систем выше или равный
второму порядку, переходный процесс имеет
вид:
13

14.

По кривой переходного процесса определяют
следующие параметры качества:
1. Время регулирования tрег – это минимальное
время вхождения кривой переходного процесса в
заданную зону точности. Как правило это область
+-5%.
hmax 1 hуст
*100%, G – перерегулирование;
2. G h
уст
3. tmax1 – время достижения первого максимума;
4. Т – период колебания системы.
Из графика переходного процесса следует, чем
быстрее система достигает максимального
значения, тем она ближе к границе устойчивости.
Чем больше частота колебаний системы, тем она
14
ближе к границе устойчивости.

15.

Анализ качества регулирования по ЛАЧХ
Рассмотрим систему первого порядка
передаточной функцией: W ( p) K
p
с
p
W ( p)
K
1
1
Wз ( p )
1
p W ( p) p K
1 pT
p 1
K
Полученная система представляет собой
инерциальное звено. Характеристика которого
имеет вид:
L(ω)
H(t)
L( ) 20 lg K 20 lg
K
-20 дб/дек
ω
t
ωCp=K
15

16.

Пусть передаточная функция имеет вид:
Wp
K
(1 pT ) p
K
K
Wз
2
p * (1 pT ) K p T p K
1
p2
T
1
p 1
K
K
Данная передаточная функция совпадает с
передаточной функцией колебательного звена,
имеющего вид:
1
Wk ( p) 2 2
p Tk 2 pTk 1
Где - декремент затухания, характеризующий
вид переходного процесса.(При
< 0,5
переходный процесс резкоколебательный, при
дз=0,5
– колебательный, при
> 0,707
переходный процесс монотонный.
16

17.

Установим
связь
между
параметрами
рассматриваемой системы и колебательного
звена.
Tk
2
T
K
2 Tk
1
K
0.5
Tk * K
0.5
K *T
Для рассматриваемой системы возможны
следующие варианты прохождения ЛАЧХ :
17

18.

а)
L(ω)
-20 дб/дек
ω
ωc=1/T
ωCp
-40 дб/дек
c cp K KT 1
0.5
Так как 0.5 ,то в системе разноколебательный
процесс и запас по фазе меньше 45 градусов.
18

19.

б)
L(ω)
-20 дб/дек
KT 1
ωc=1/T=ωCp=K
ω
0.5
-40 дб/дек
Запас по фазе равен 45 градусов. В системе
колебательный
процесс
с
меньшей
амплитудой, чем в 1 случае.
19

20.

в)
L(ω)
-20 дб/дек
ωCp=K
ωc=1/T
ω
KT 1
0.5
-40 дб/дек
Запас по фазе больше 45 градусов. В
системе может наблюдаться незначительный
колебательный переходный процесс или же
монотонный переходный процесс. Очевидно,
чем на большем расстоянии находится ωср и
ωс, тем ТК<1, а величина
0,707.
будет стремиться к
20

21.

Вывод:
для
достижение
системой
требуемого
качества
регулирования
необходимо, что бы логарифмическая
характеристика
заданной
системы
пересекала частотную ось под углом 20дб/дек и чем на большем удалении будет
находиться ωср и ωс , тем переходный
процесс будет более стремиться к
монотонному, и запас по фазе у такой
системы должен быть больше 45 градусов.
21