Основы теории вероятности/ Основные понятия и определения

1.

Основы теории
вероятности
Основные понятия и
определения

2.

В современном мире автоматизации производства
теория вероятности(Т.В) необходима специалистам
для решения задач, связанных с выявлением
возможного хода процессов, на которые влияют
случайные факторы(например, ОТК: сколько
бракованных изделий будет изготовлено). Возникла
Т.В. в 17 веке в переписке Б. Паскаля и П.Ферма, где
они производили анализ азартных игр. Советские и
русские ученые также принимали участие в развитии
этого раздела математики: П.Л. Чебышев, А.А. Марков,
А.М. Ляпунов, А.Н. Колмогоров.

3.

Определение
Под случайным событием понимается
всякое явление, о котором имеет смысл
говорить, что оно происходит или не
происходит.
Событиями являются результатами различных опытов,
измерений, наблюдений.

4.

Примеры:
1)Из ящика с разноцветными шарами наугад
вынимают черный шар.
2)При бросании игральной кости выпала цифра 7.
3)При телефонном вызове абонент оказался занят.
4)Попадание в мишень при выстреле
5)Выпущенное изделие оказалось бракованным
6)Извлечь из колоды карт туза пик
Случайные события обозначаются большими латинскими
буквами A, B, C,…

5.

Достоверным назовем событие которое обязательно
произойдет при выполнении определенного
количества условий.
Невозможным назовем событие которое не
происходит при выполнении определенного
количества условий.
Пример:
1. Извлечение белого шара из ящика, в котором все шары
белые
2. Извлечение черного шара из ящика, в котором все шары
белые

6.

Два события называются несовместными, если
появление одного из них исключает появление
другого. В противном случае события называются
совместными.

7.

Примеры:
1) При подбрасывании монеты появление решки
исключает одновременное появление орла:
А появление
В появление
О,
решки Р,
орла
несовместные
события.
2) Есть билет лотереи «Русское лото»:
А билет
В билет
выиграшный,
невыигрышный,
несовместные
3) Извлечение карты из колоды
А – извлечь туза
В – извлечь пиковую масть
совместные события
события.

8.

Если возможные исходы (результаты) опыта являются событиями
несовместными, достоверными, то каждый из результатов испытания назовем
элементарным исходом. Те элементарные исходы, при которых интересующее
нас событие наступает назовем благоприятствующими этому событию
исходами.
Классическое определение вероятности
Вероятностью события А называется отношение числа
m элементарных исходов, благоприятствующих этому
событию, к общему числу элементарных исходов
испытания n.
Обозначение:
m
p P(a )
n

9.

Свойства
10. 0 P ( a ) 1.
20. Для достоверного события m=n и P(a)=1.
30. Для невозможного события m=0 и P(a)=0.

10. Примеры

1. Найти вероятность выпадения числа, кратного 3
на игральной кости
2. Монету подбрасывают 3 раза. Найти вероятность
того, что
а) орел выпадет 2 раза
б) орел выпадет хотя бы 2 раза
3. Брошены 2 игральные кости. Какова вероятность
события А- выпадения в сумме не менее 9 очков.
4. Куб, все грани которого окрашены, распилен на
1000 кубиков одинакового размера, которые затем
одинаково перемешаны. Найти вероятность того,
что на удачу извлечённый кубик имеет 2
окрашенные грани

11. Задача №1

А – выпадет число, кратное 3.
m
p ( A)
n
- число всех возможных исходов при подбрасывании кубика
n 6
m 2
- число очков, кратных 3 ( 3 и 6)
2 1
p ( A)
6 3
Ответ: 1/3

12. Задача №2

А – орел выпадет 2 раза.
m
p ( A)
n
Для нахождения m и n составим дерево исходов.
n 8, m 3
3
p( A)
8
В – орел выпадет хотя бы 2 раза означает, что
он выпадет 2 или более раз.
n 8, m 4
4
p ( B ) 0,5
8

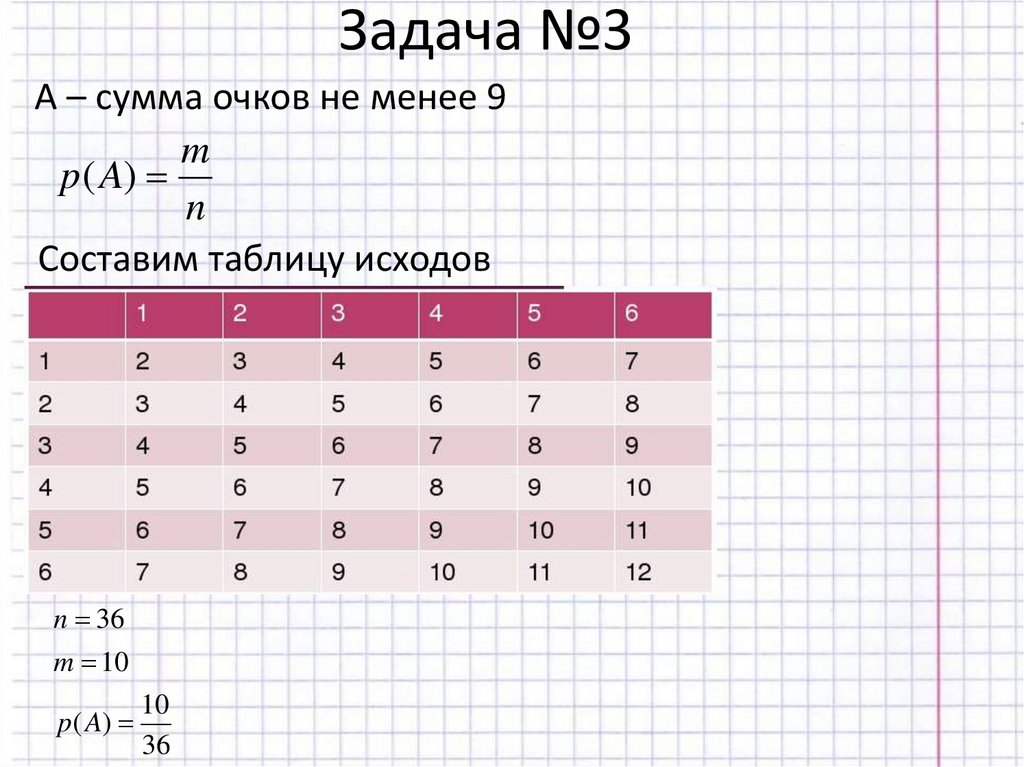
13. Задача №3

А – сумма очков не менее 9
m
p ( A)
n
Составим таблицу исходов
n 36
m 10
p ( A)
10
36

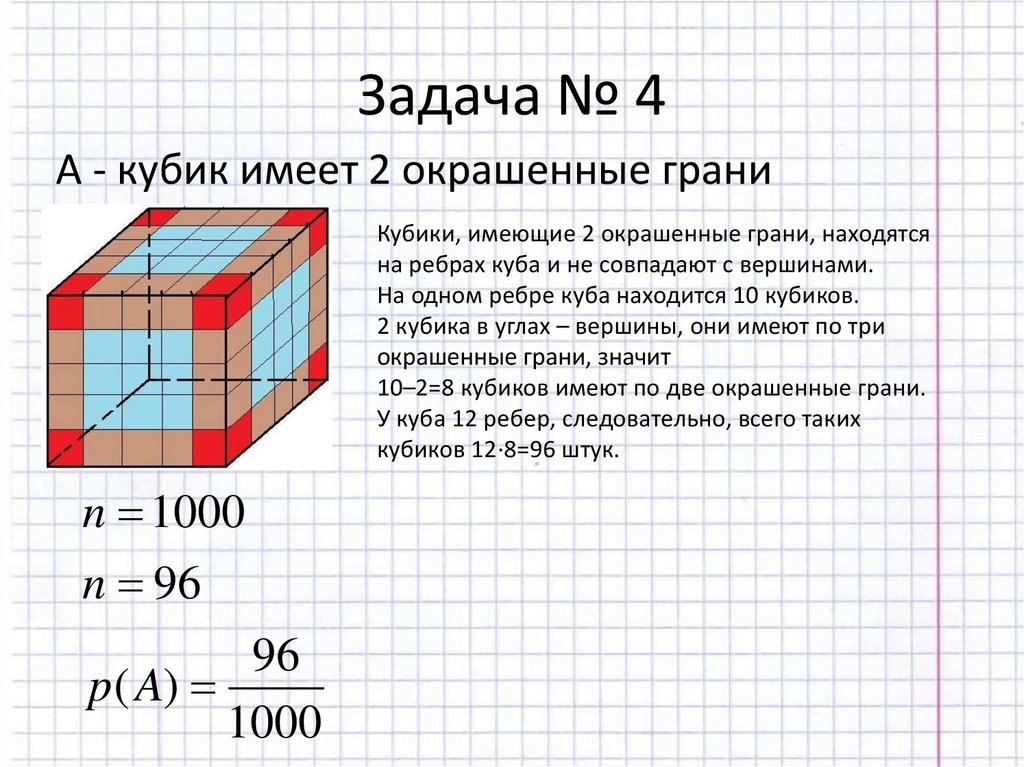
14. Задача № 4

А - кубик имеет 2 окрашенные грани
Кубики, имеющие 2 окрашенные грани, находятся
на ребрах куба и не совпадают с вершинами.
На одном ребре куба находится 10 кубиков.
2 кубика в углах – вершины, они имеют по три
окрашенные грани, значит
10–2=8 кубиков имеют по две окрашенные грани.
У куба 12 ребер, следовательно, всего таких
кубиков 12·8=96 штук.
n 1000
n 96
96
p ( A)
1000

15.

Статистическое определение
вероятности
При многократном повторении опыта частота события
принимает значения, близкие к некоторому постоянному
числу. Например, при многократном бросании игральной
кости частота выпадения каждого из чисел очков от 1 до 6
1
колеблется около числа
6
Многократно проводились опыты бросания однородной
монеты, в которых подсчитывали число появления «герба», и
каждый раз, когда число опытов достаточно велико, частота
1
события «выпадения герба» незначительно отличалась от 2

16.

Число
бросаний
Число
выпадений
герба
Частота
Ж. Бюффон
4040
2048
0,5080
К. Пирсон
12000
6014
0,5016
К. Пирсон
24000
12012
0,5006
Экспериментатор

17. Условия статистического определения

• 1. Рассматриваемые события должны быть
исходами только тех испытаний, которые могут
быть воспроизведены неограниченное число раз
при одном и том же комплексе условий.
• 2. События должны обладать так называемой
статистической устойчивостью, или
устойчивостью относительных частот.
• 3. Число испытаний, в результате которых
появляется событие А, должно быть достаточно
велико, ибо только в этом случае можно считать
вероятность события Р(А) приближенно равной ее
относительной частоте.

18. Геометрическое определение вероятности

• Пусть фигура g является частью некоторой
фигуры G. Пусть нужно найти вероятность
попадания брошенной точки в область g.
Обозначим mes меру области ( длину, площадь,
объем), тогда
• Геометрической вероятностью события А
называется отношение меры области,
благоприятствующей появлению события А, к
мере всей области, т.е.
mesg
p ( A)
mesG

19. Пример

В квадрат вписана окружность. Найти
вероятность того, что наудачу взятая
точка в квадрате окажется лежащей
внутри окружности.

20.

Дома:
1. Монета бросается 3 раза подряд. Найти вероятность
событий: А- число выпадений герба больше числа
выпадений решки; В- выпадает два герба; Срезультаты всех бросаний одинаковы.
2. Из урны, в которой находится 3 белых, 4 чёрных и 5
красных шаров, наудачу вынимается один шар.
Какова вероятность событий: А- появление белого
шара; В – появление чёрного шара; С- появление
жёлтого шара; D- появление красного шара.