Численное решение одномерных задач динамики сплошных сред с учетом симметрии

1.

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение
высшего образования
«Национальный исследовательский
Нижегородский государственный университет им. Н.И. Лобачевского»
(ННГУ)
Институт информационных технологий, математики и механики
Кафедра теоретической, компьютерной и экспериментальной механики
Направление подготовки 01.03.02 Прикладная математика и информатика
Направленность (профиль) программы бакалавриата: Математическое моделирование и вычислительная математика
« Численное решение одномерных задач динамики сплошных сред с учетом
симметрии»
Выполнил: студент группы 381803-3
Орлов Никита Алексеевич
Руководитель: доцент кафедры теоретической, компьютерной и экспериментальной механики,
к.ф.-м.н. Нагорных Елена Владимировна
Нижний Новгород
2022

2. Цель и задачи

Цель выпускной квалификационной работы – изучить вариационно-разностный
метод решения одномерной задачи динамической теории упругости.
В связи с этим были поставлены следующие задачи:
1.Вывод определяющей системы уравнений динамического деформирования упругой
сплошной среды в одномерной постановке (одноосная деформация) с учетом
симметрии.
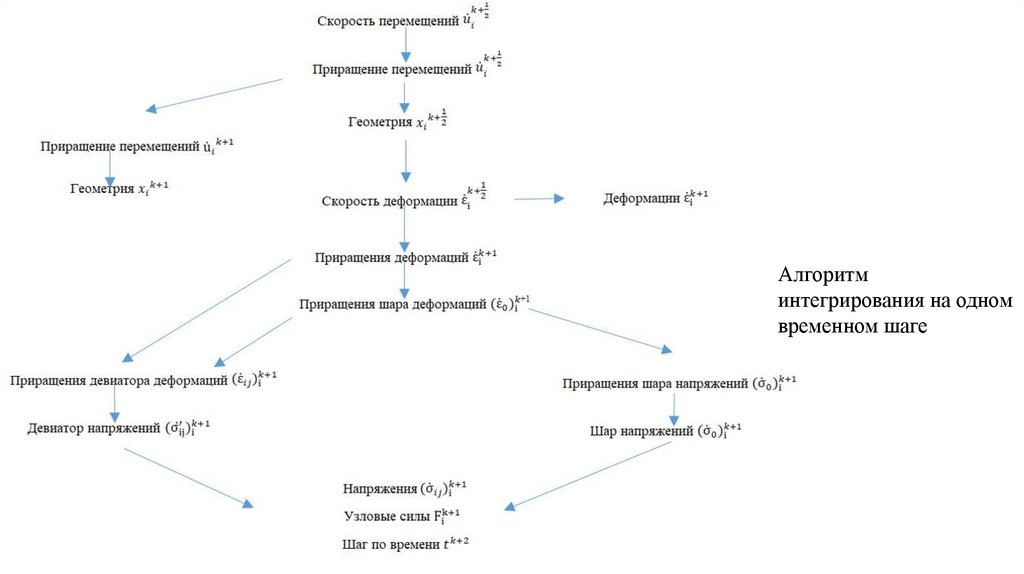
2.Изучение метода построения численной схемы для решения полученной системы на
основе вариационно-разностного метода.
3.Разработка алгоритма и программы численного решения определяющей системы
уравнений.
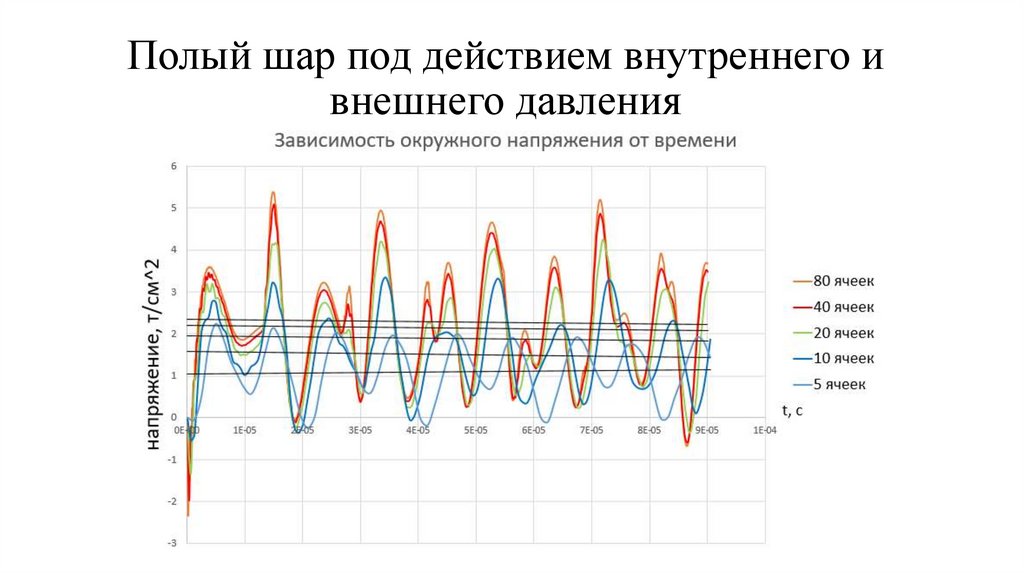
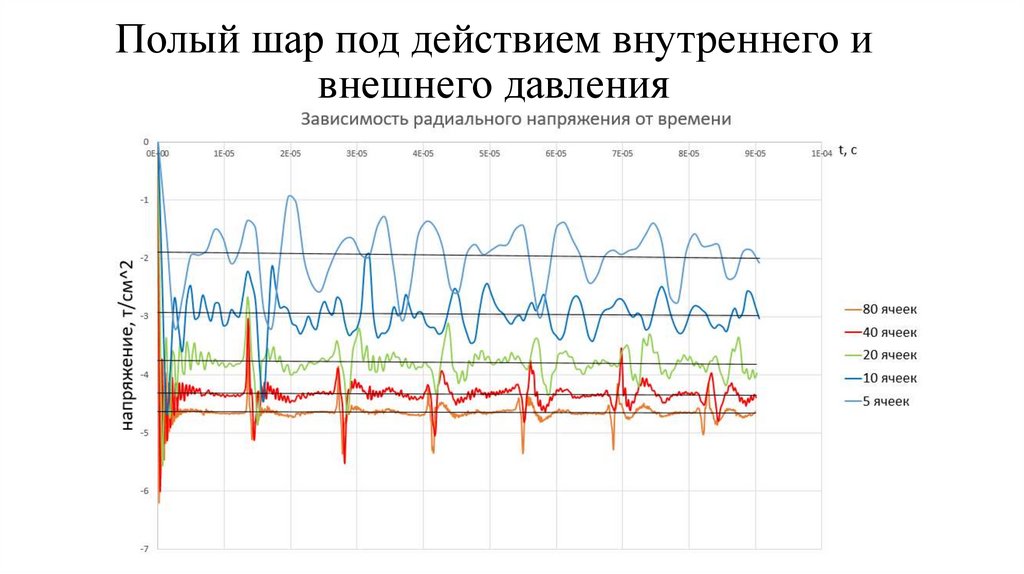
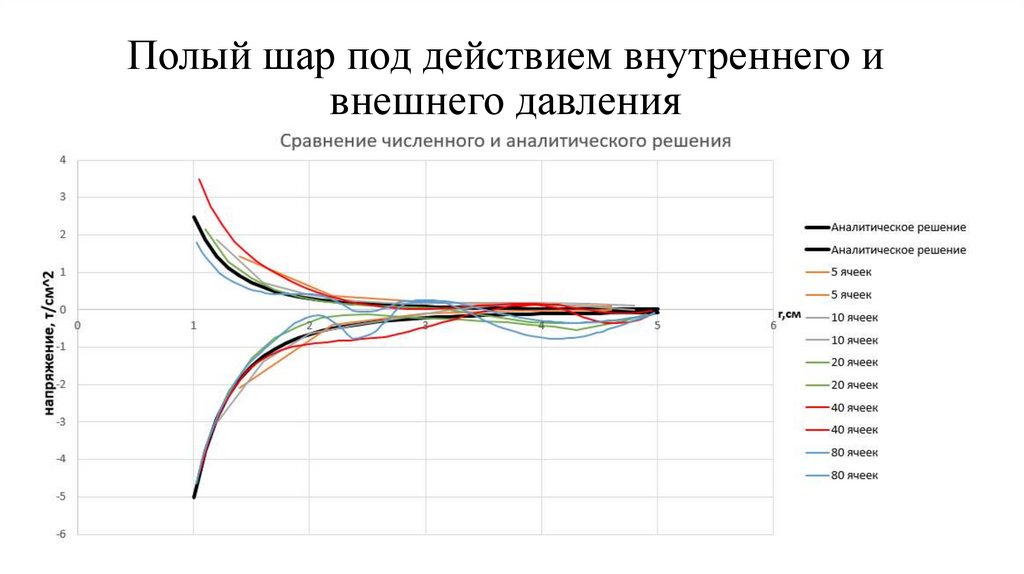
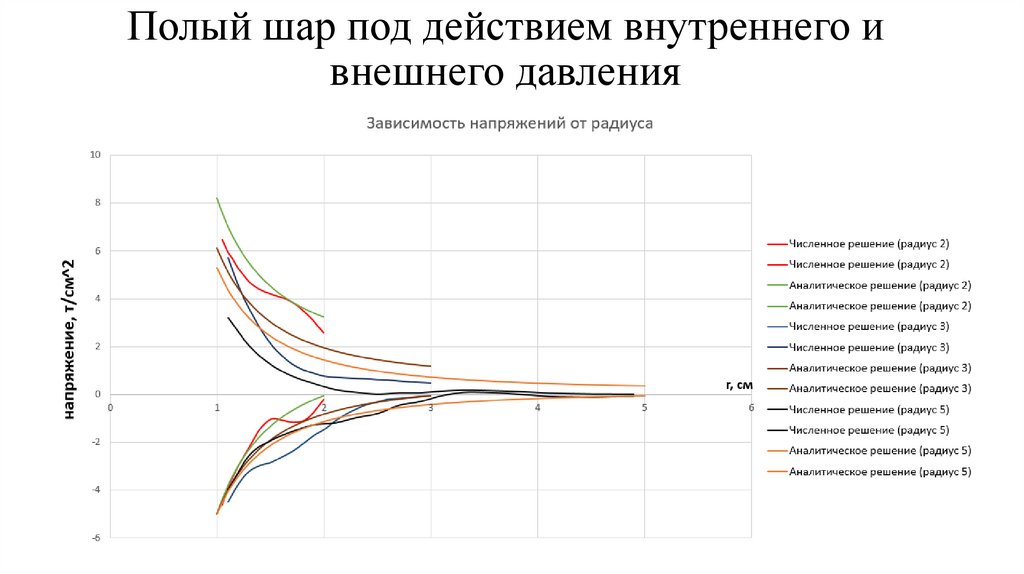
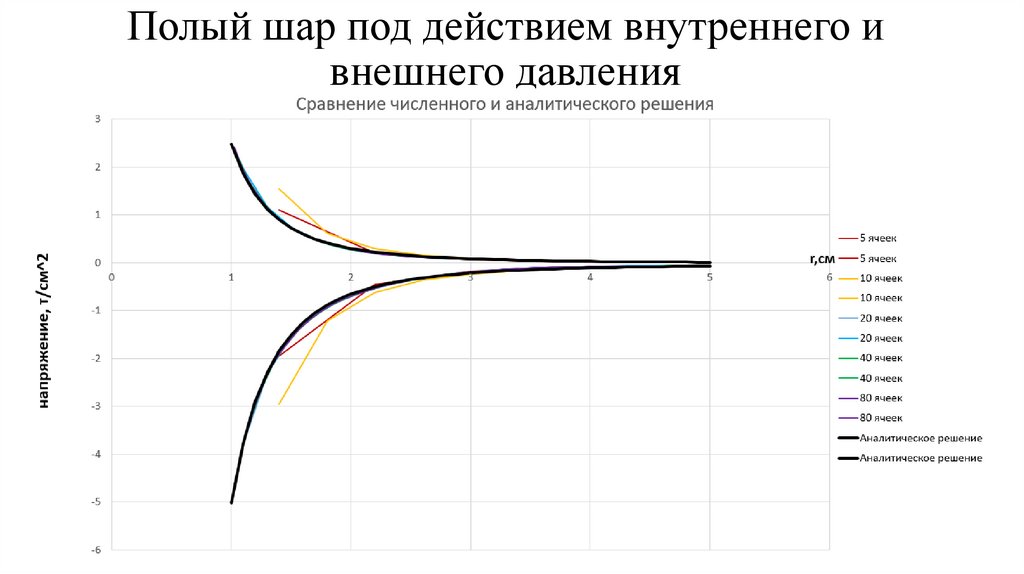
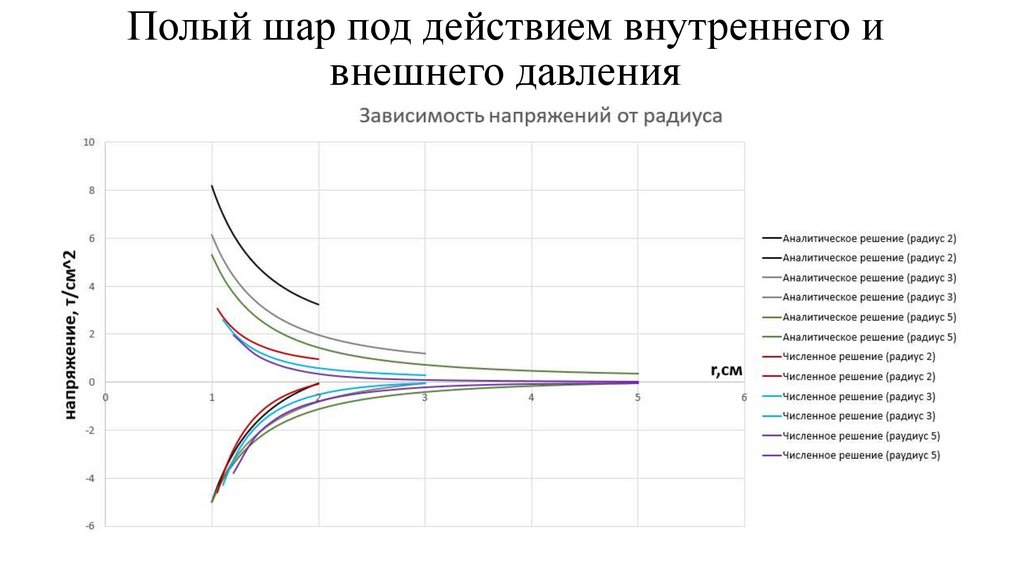
4. Тестирование программы на задаче о деформировании полого упругого шара под
действием внешнего и внутреннего давления. Сравнение полученного численного
решения с аналитическим решением.

3. Постановка задачи

Определяющая система уравнений включает в
себя кинематические соотношения, уравнения
состояния среды (физические соотношения),
уравнение движения, начальные и кинематические
граничные условия. Рассматривается
геометрически и физически линейная постановка
задач динамики упругих сред.

4. Определяющая система уравнений динамической теории упругости в трехмерной постановке. Тензор деформации

Вектор перемещения:
ux = ux x, y, z
u