Similar presentations:
Кинематика движения материальной точки и абсолютно твердого тела (лекция 1)
1. ФИЗИКА
Раздел 1 – механикаЛекция 1. ВВЕДЕНИЕ.
КИНЕМАТИКА ДВИЖЕНИЯ Материальной точки и
Абсолютно твердого тела
Авторы: Сидоренко Ф.А., Попель П.С., Барбин Н.М.
2.
1. Учебник:Т.И.Трофимова. Курс физики.
Москва.:
Высшая школа (все годы издания).
Задачник:
Волькенштейн В.Г. Сборник задач
по общей физике.
2
3. 1. Механика
Разделы механики в нашем курсе:1.1
КИНЕМАТИКА ДВИЖЕНИЯ М.Т. И А.Т.Т.
1.2
ДИНАМИКА ДВИЖЕНИЯ М.Т. И
ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ А.Т.Т.
1.3
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
1.4
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И РАБОТА
1.5
СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
3
4. КИНЕМАТИКА ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ (М.Т.)
Цель – пространственно-временное описание движенияВводные понятия
М.т. (материальная точка) – физический объект, размерами
которого можно пренебречь по сравнению с расстояниями
до других тел, рассматриваемых в задаче.
А.т.т. (абсолютно твердое тело) – абсолютно не деформируемое
тело, или тело, расстояние между двумя любыми точками
которого остается постоянным при его движении.
Траектория движения – линия, по которой движется м.т.
4
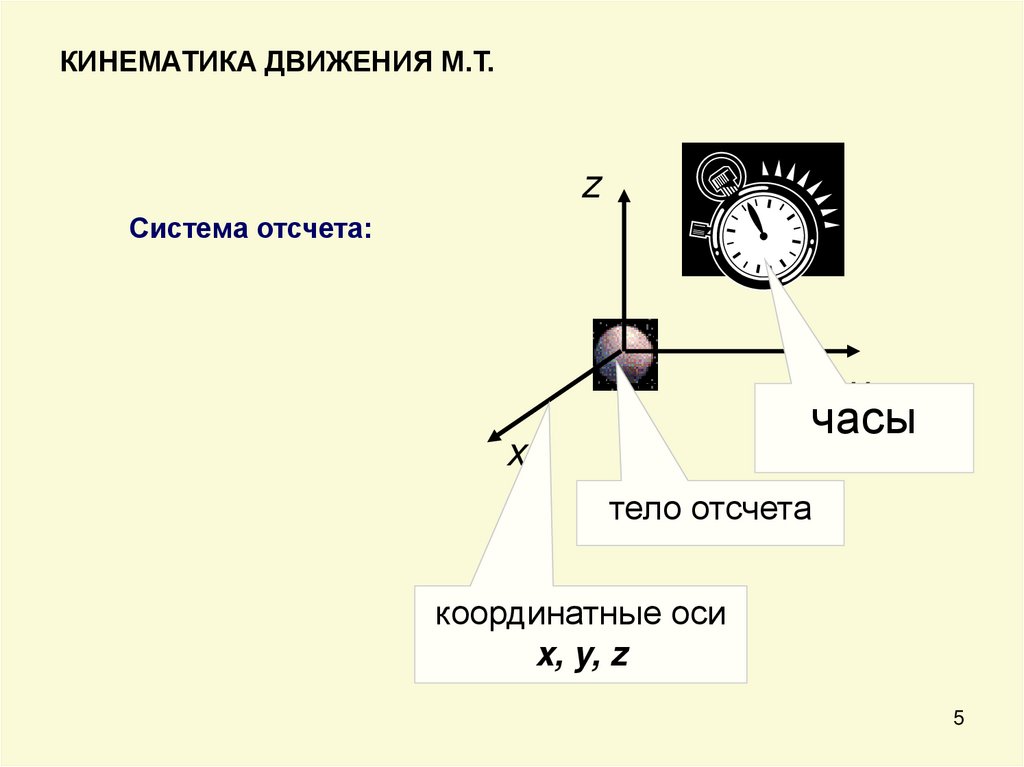
5. КИНЕМАТИКА ДВИЖЕНИЯ М.Т.
zСистема отсчета:
y
часы
x
тело отсчета
координатные оси
x, y, z
5
6.
Положение м.т. относительно СО можно задать:а) радиусом-вектором
системы отсчета;
r , проведенным к м.т. из начала O
б) тремя координатами x, y, z – проекциями радиуса-вектора r
на координатные оси: x = rx, y = ry, z = rz.
6
7.
Положение м.т. относительно СО можно задать:а) радиусом-вектором
системы отсчета;
r , проведенным к м.т. из начала O
б) тремя координатами x, y, z – проекциями радиуса-вектора r
на координатные оси: x = rx, y = ry, z = rz.
7
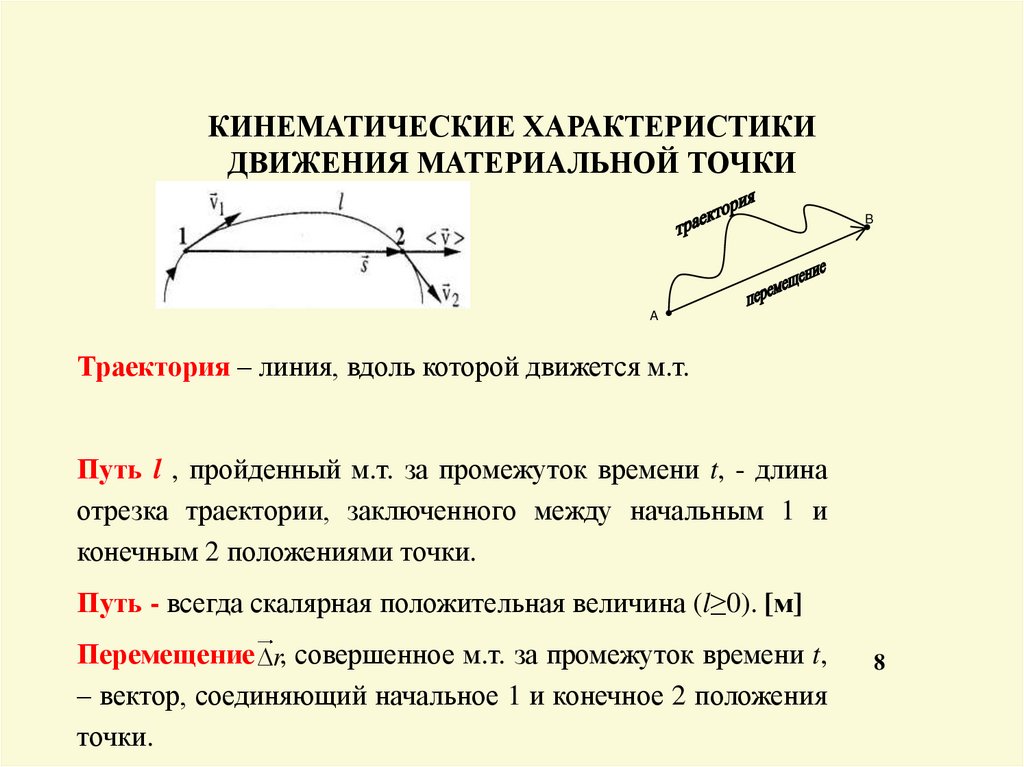
8. КИНЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
BA
Траектория – линия, вдоль которой движется м.т.
Путь l , пройденный м.т. за промежуток времени t, - длина
отрезка траектории, заключенного между начальным 1 и
конечным 2 положениями точки.
Путь - всегда скалярная положительная величина (l≥0). [м]
Перемещение r, совершенное м.т. за промежуток времени t,
– вектор, соединяющий начальное 1 и конечное 2 положения
точки.
8
9. СКОРОСТЬ
1. Средняя скорость– векторная
физическая
величина
(ВФВ),
характеризующая среднюю быстроту
изменения со временем перемещения
точки и равная отношению приращения
радиуса-вектора r r2 r1
точки к
промежутку времени ∆t, за которое это
приращение произошло:
r
t
м
с
2. Средняя путевая скорость
- скалярная физическая
величина (СФВ), характеризующая быстроту изменения пути l
и равная отношению пути, пройденного материальной точкой,
ко времени движения l
t
9
10.
3. Мгновенная скорость при ∆t→0 равна:lim
t 0
r
dr
t
dt
Мгновенная скорость м.т. – это скорость в данный момент
времени или в данной точке пространства, равная производной
радиус-вектора м.т. по времени.
В каждой точке траектории мгновенная скорость направлена
по касательной к траектории.
4. Модуль мгновенной скорости равен производной вектора
перемещения, или пути по времени
lim
t 0
r
l
dl
lim
t 0 t
t
dt
10
11. УСКОРЕНИЕ
Быстроту изменения скоростихарактеризует ускорение [м/с2].
с
течением
времени
Средним ускорением неравномерного движения в интервале от t
до t+∆t называется ВФВ, равная отношению изменения скорости
к интервалу времени ∆t , за который это изменение произошло:
a
.
t
Мгновенным ускорением
материальной точки в момент
времени t будет предел среднего
ускорения:
a
d
a lim a lim
t 0
t 0 t
dt
Мгновенное
ускорение м.т. – ВФВ, характеризующая
мгновенную быстроту изменения скорости точки со временем и
равная производной скорости по времени.
11
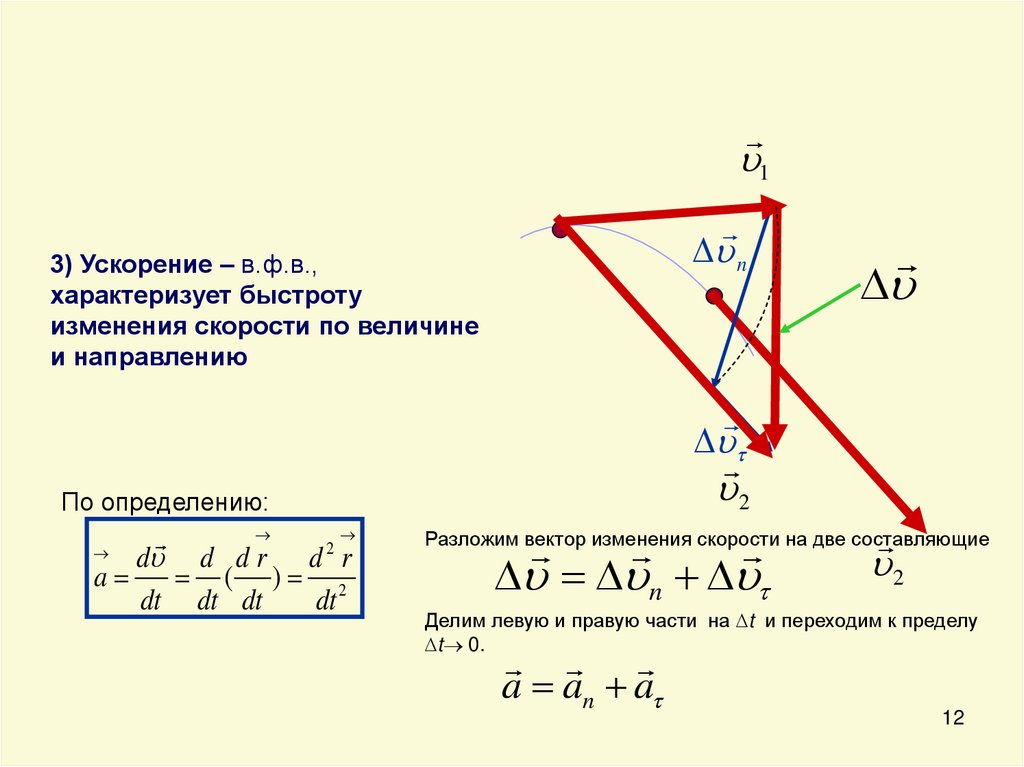
12.
1n
3) Ускорение – в.ф.в.,
характеризует быстроту
изменения скорости по величине
и направлению
2
По определению:
d d d r d r
a
( ) 2
dt dt dt
dt
2
Разложим вектор изменения скорости на две составляющие
n
2
Делим левую и правую части на t и переходим к пределу
t 0.
a an a
12
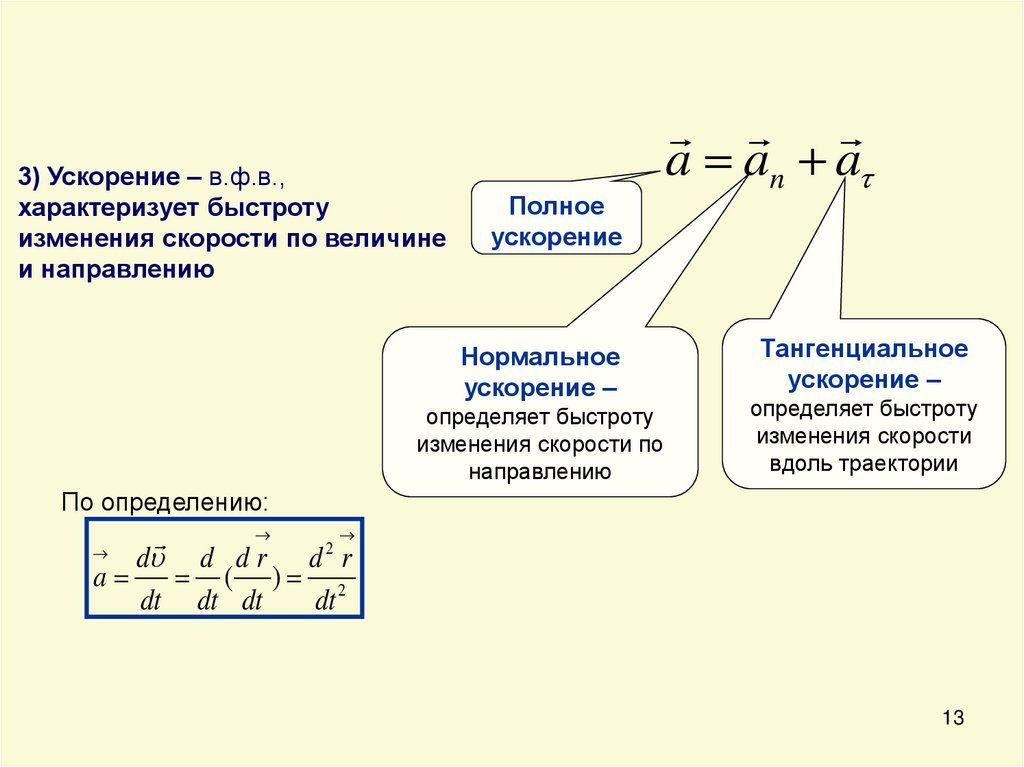
13.
3) Ускорение – в.ф.в.,характеризует быстроту
изменения скорости по величине
и направлению
Полное
ускорение
Нормальное
ускорение –
определяет быстроту
изменения скорости по
направлению
a an a
Тангенциальное
ускорение –
определяет быстроту
изменения скорости
вдоль траектории
По определению:
a
d d d r d r
( ) 2
dt dt dt
dt
2
13
14.
a an aДля решения задач – формулы в скалярном виде:
3) Ускорение – в.ф.в.,
характеризует быстроту
изменения скорости по величине
и направлению
a
2
an
R
a a 2 an2
По определению:
d
a
dt
d d d r d r
( ) 2
dt dt dt
dt
2
Модуль полного ускорения
14
15. ВИДЫ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Поступательное движение – это движение,при котором любая прямая, жестко связанная
с движущимся телом, остается параллельной
своему первоначальному положению.
Вращательное движение – это движение,
при котором все точки тела движутся по
окружности, центры которых лежат на одной
и той же прямой, называемой осью
вращения.
15
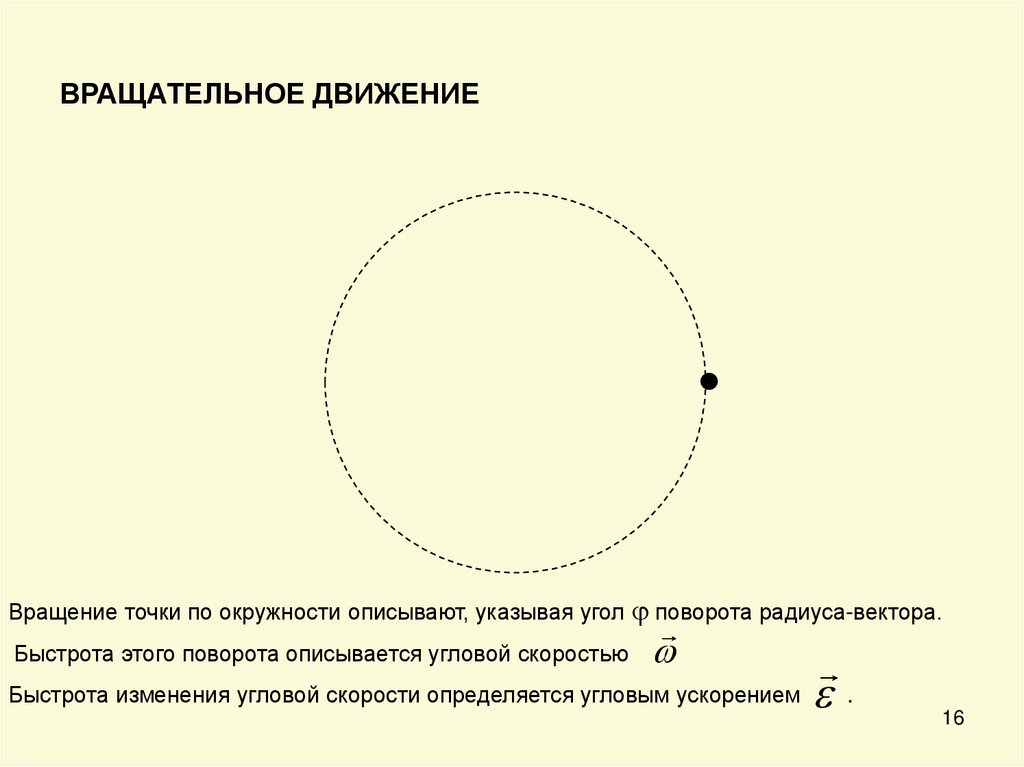
16. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
Вращение точки по окружности описывают, указывая уголБыстрота этого поворота описывается угловой скоростью
поворота радиуса-вектора.
Быстрота изменения угловой скорости определяется угловым ускорением
.
16
17.
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕПусть м.т. движется по окружности радиуса
из точки 1 в
точку 2.
Её положение через промежуток времени
задаётся углом
.
Модуль вектора равен углу поворота , а его направление
совпадает с направлением поступательного движения острия
винта, головка которого вращается в направлении движения
точки по окружности, т.е. подчиняется правилу правого винта.
17
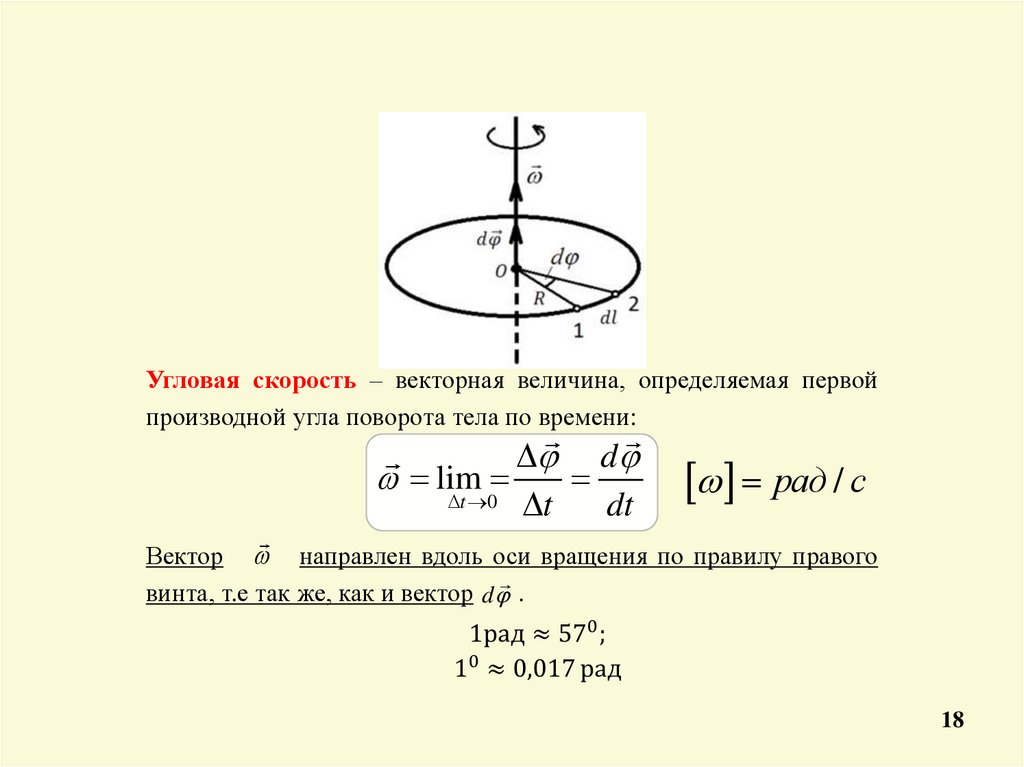
18.
Угловая скорость – векторная величина, определяемая первойпроизводной угла поворота тела по времени:
lim
t 0
d
t
dt
рад / с
Вектор направлен вдоль оси вращения по правилу правого
винта, т.е так же, как и вектор d .
18
19. УГЛОВОЕ УСКОРЕНИЕ
d0
dt
d
0
dt
При ускоренном
движении вектор
сонаправлен
вектору , при
замедленном –
противонаправле
н ему.
Угловая ускорение – ВФВ, характеризующая быстроту
изменения угловой скорости, определяемая первой производной
угловой скорости по времени:
рад
d
с2
dt
19
20.
Тангенциальная составляющая ускоренияa
d R
dt
R
a
d
,
dt
R.
d
R
dt
Нормальная составляющая ускорения
an
2
R
2 R2
R
2R
20
21. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
ddt
d
С конца вектора
угловой скорости
вращение выглядит
против часовой
стрелки.
Здесь – «к нам»
Куда направлен вектор углового ускорения,
если угловая скорость возрастает по модулю?
А если – убывает?
r
Если угловая
скорость
изменяется, то
это значит, что
угловое
ускорение
отличается от
нуля.
По определению:
2
d d
2
dt
dt
21
22.
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕНаправления векторов!
Определяем по правилу
для векторного
произведения
d
d
r
dr [d r ]
[ r ]
dr
Для решения задач – в скалярном виде:
an
a [ r ]
an [ ]
a
2
r , a r , an
r
23.
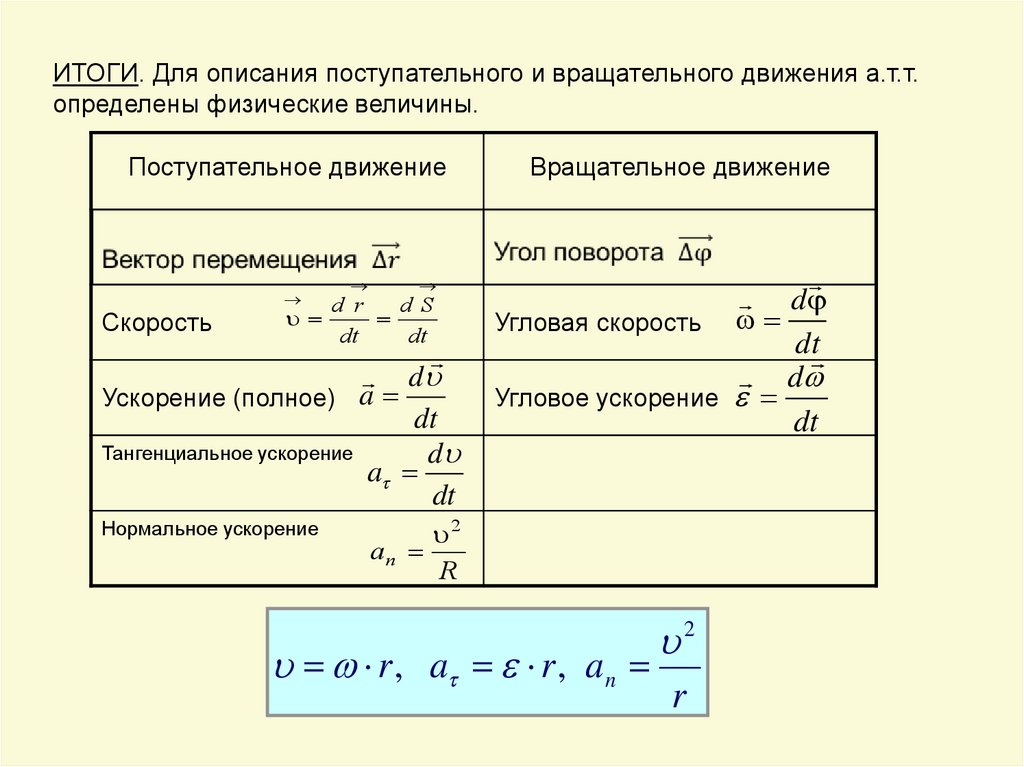
ИТОГИ. Для описания поступательного и вращательного движения а.т.т.определены физические величины.
Поступательное движение
Скорость
d r
dS
dt
dt
d
Ускорение (полное) a
dt
Тангенциальное ускорение
d
a
dt
Нормальное ускорение
Вращательное движение
d
Угловая скорость
dt
d
Угловое ускорение
dt
2
an
R
2
r , a r , an
r
















 physics
physics








