Similar presentations:
Оптимизация сетевой модели
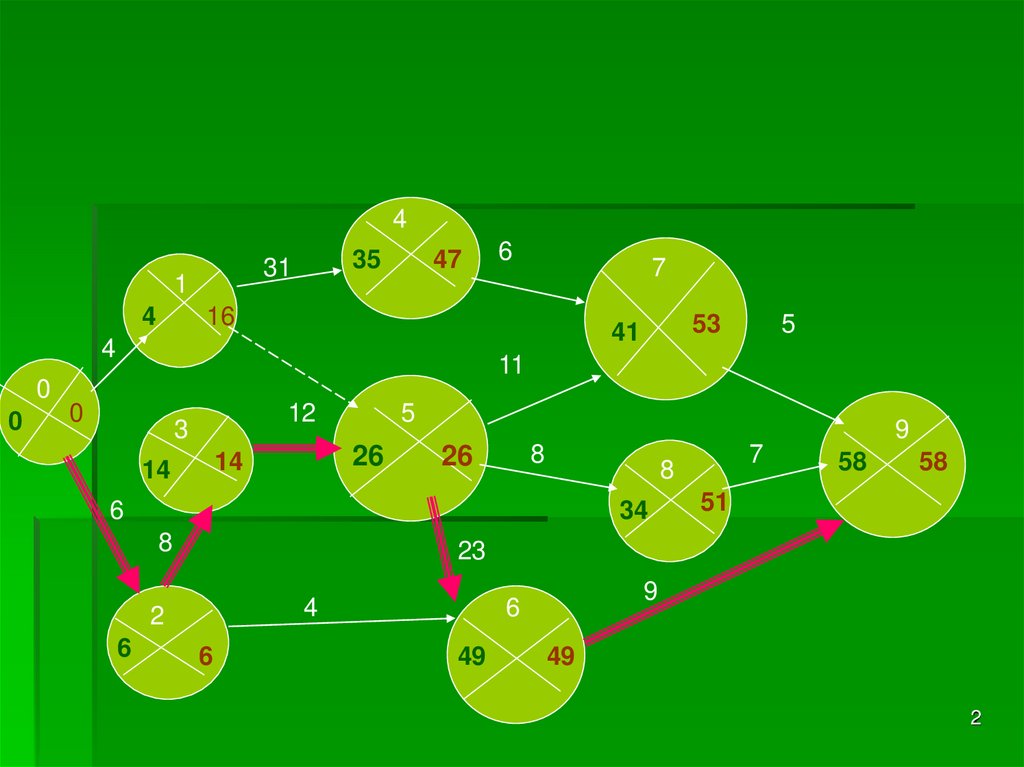
1. Оптимизация сетевой модели
12.
41
4
35
31
47
6
7
16
53
41
4
5
11
0
0
0
12
3
26
14
14
5
9
8
26
6
34
8
58
58
51
23
4
2
6
7
8
6
9
6
49
49
2
3.
Для оптимизации модели необходимы данные околичестве исполнителей каждой работы.
Ключевым элементом задачи оптимизации выступает
понятие «трудоёмкости работы».
Если работа длится tij дней (часов, месяцев и т.п.), а
выполняют её lij человек, трудоёмкость работы равна:
ij tijlij
Предполагается, что трудоёмкость работы не меняется с изменением
числа исполнителей.
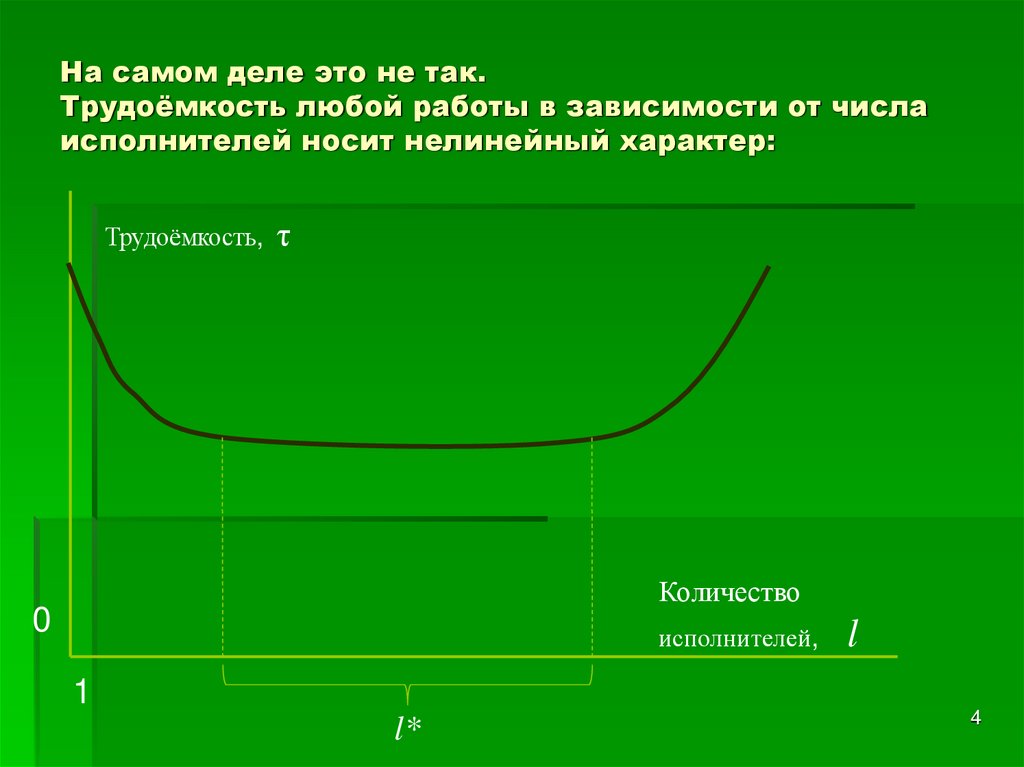
4. На самом деле это не так. Трудоёмкость любой работы в зависимости от числа исполнителей носит нелинейный характер:
Трудоёмкость,τ
Количество
0
исполнителей,
1
l*
l
4
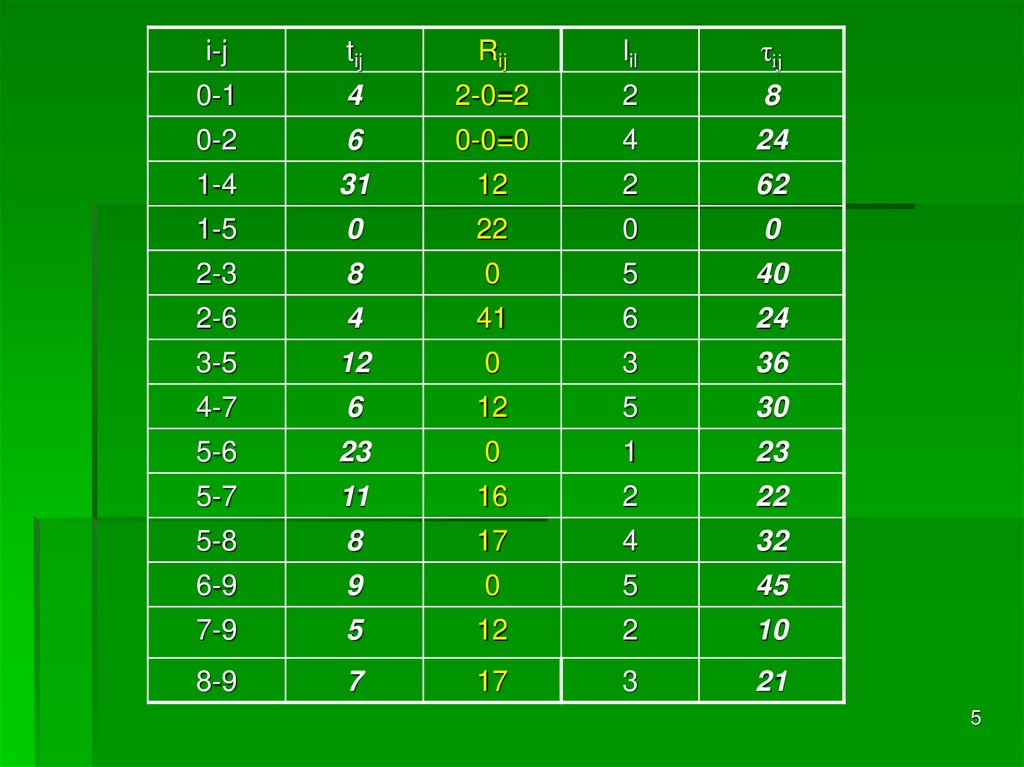
5.
i-jtij
Rij
lil
τij
0-1
4
2-0=2
2
8
0-2
6
0-0=0
4
24
1-4
31
12
2
62
1-5
0
22
0
0
2-3
8
0
5
40
2-6
4
41
6
24
3-5
12
0
3
36
4-7
6
12
5
30
5-6
23
0
1
23
5-7
11
16
2
22
5-8
8
17
4
32
6-9
9
0
5
45
7-9
5
12
2
10
8-9
7
17
3
21
5
6.
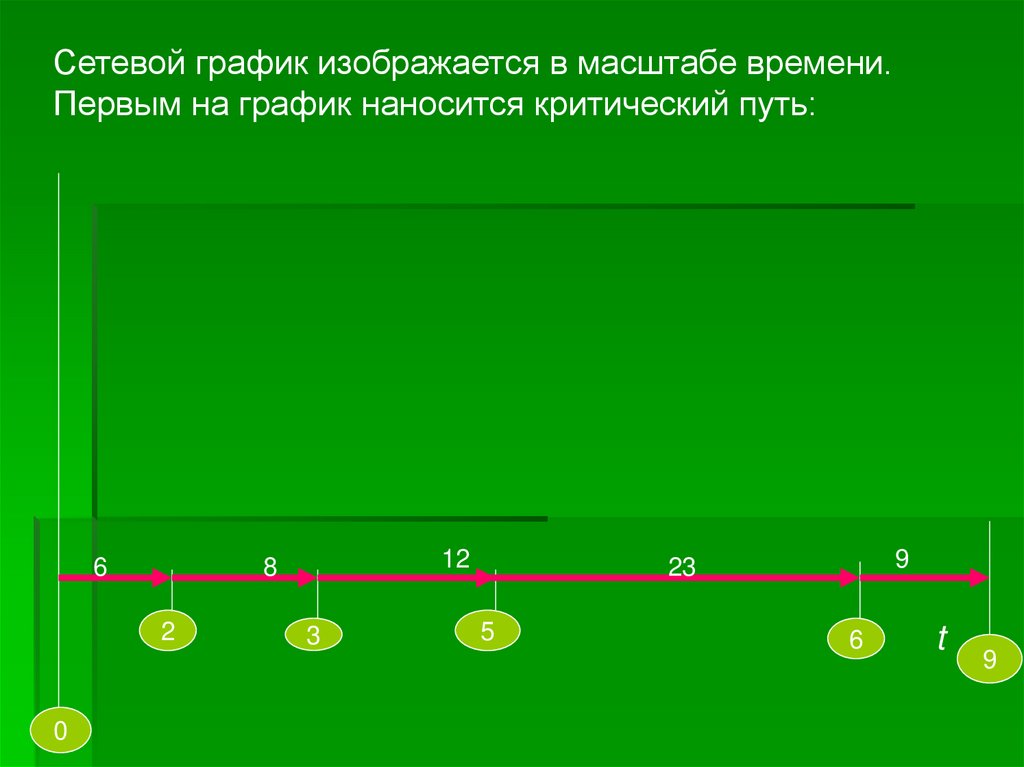
Сетевой график изображается в масштабе времени.Первым на график наносится критический путь:
6
2
0
12
8
3
9
23
5
6
t
9
7.
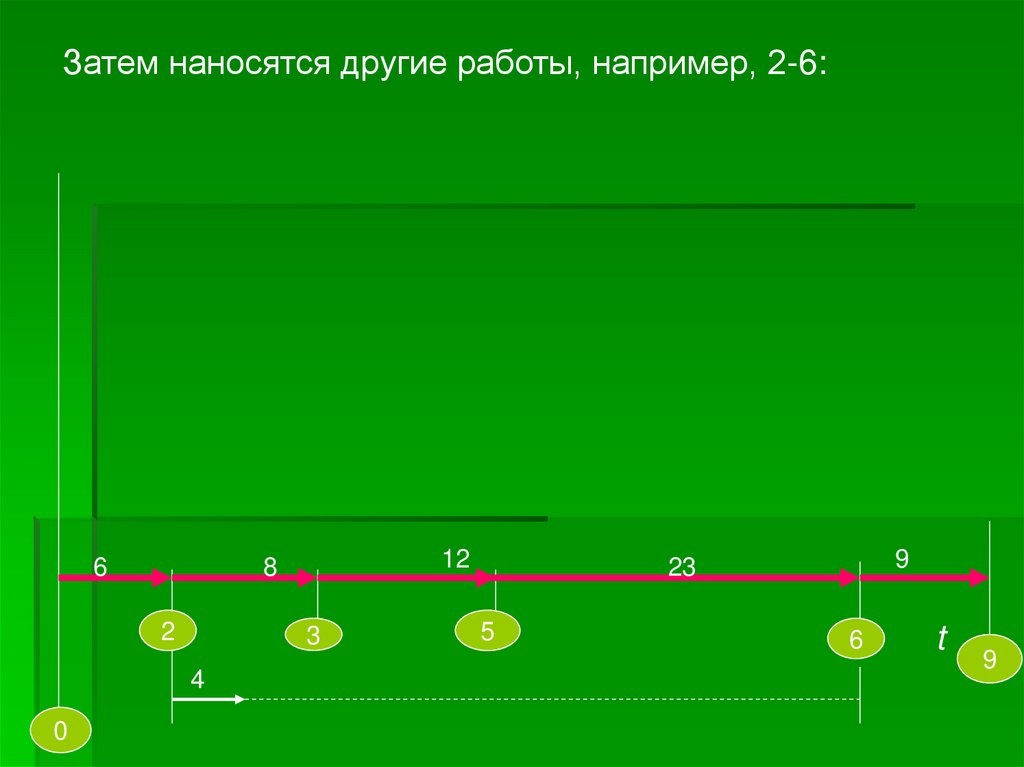
Затем наносятся другие работы, например, 2-6:6
2
3
4
0
12
8
9
23
5
6
t
9
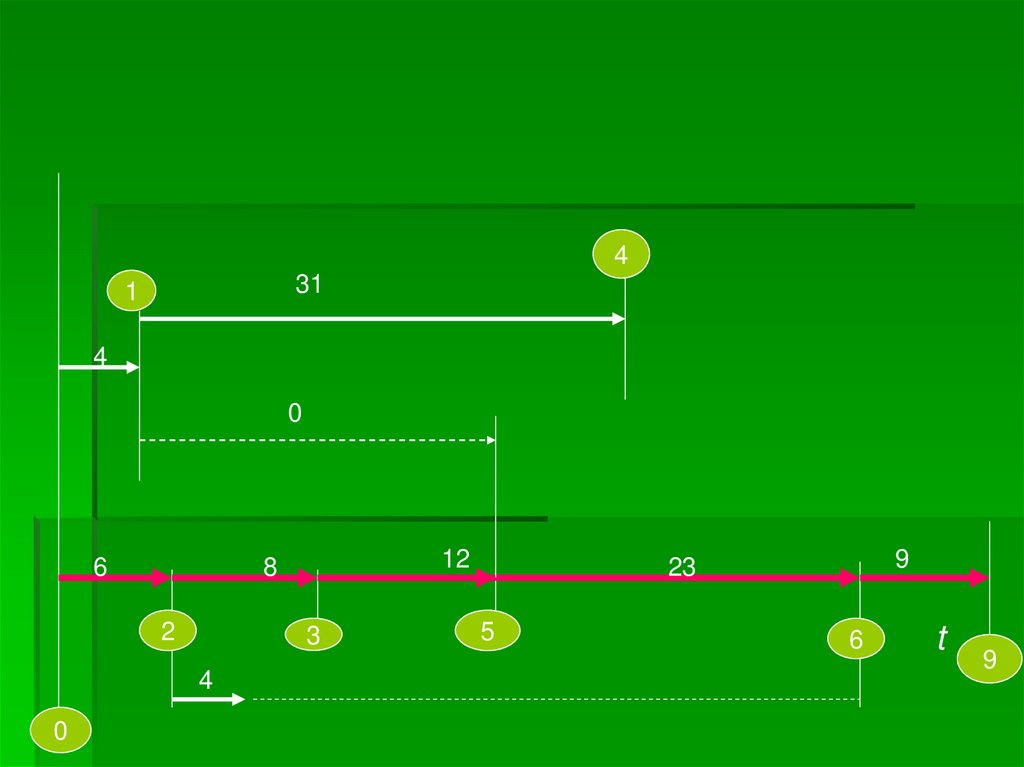
8.
431
1
4
0
6
2
3
4
0
12
8
9
23
5
6
t
9
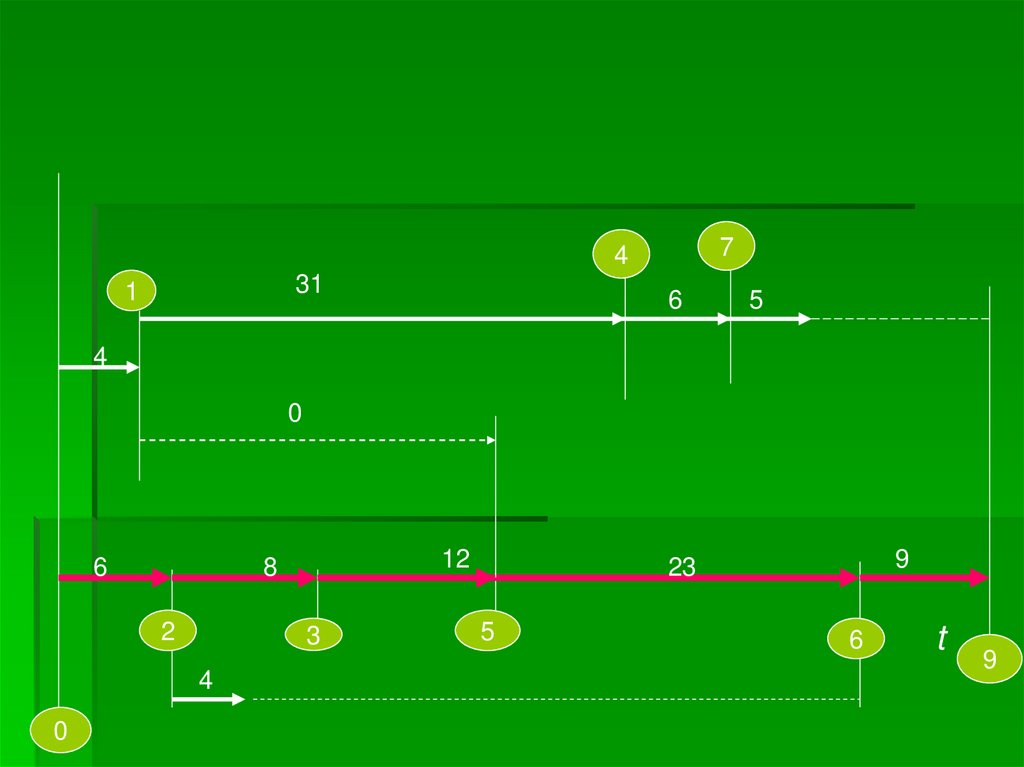
9.
74
31
1
6
5
4
0
6
2
3
4
0
12
8
9
23
5
6
t
9
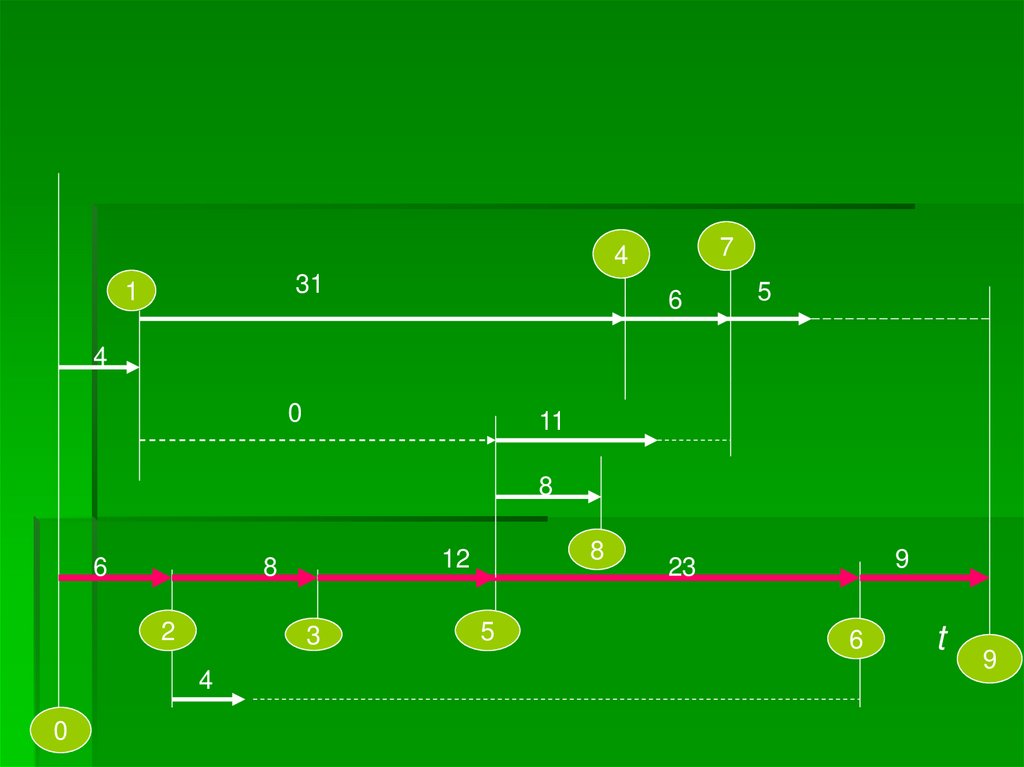
10.
74
31
1
6
5
4
0
11
8
6
2
3
4
0
8
12
8
5
9
23
6
t
9
11.
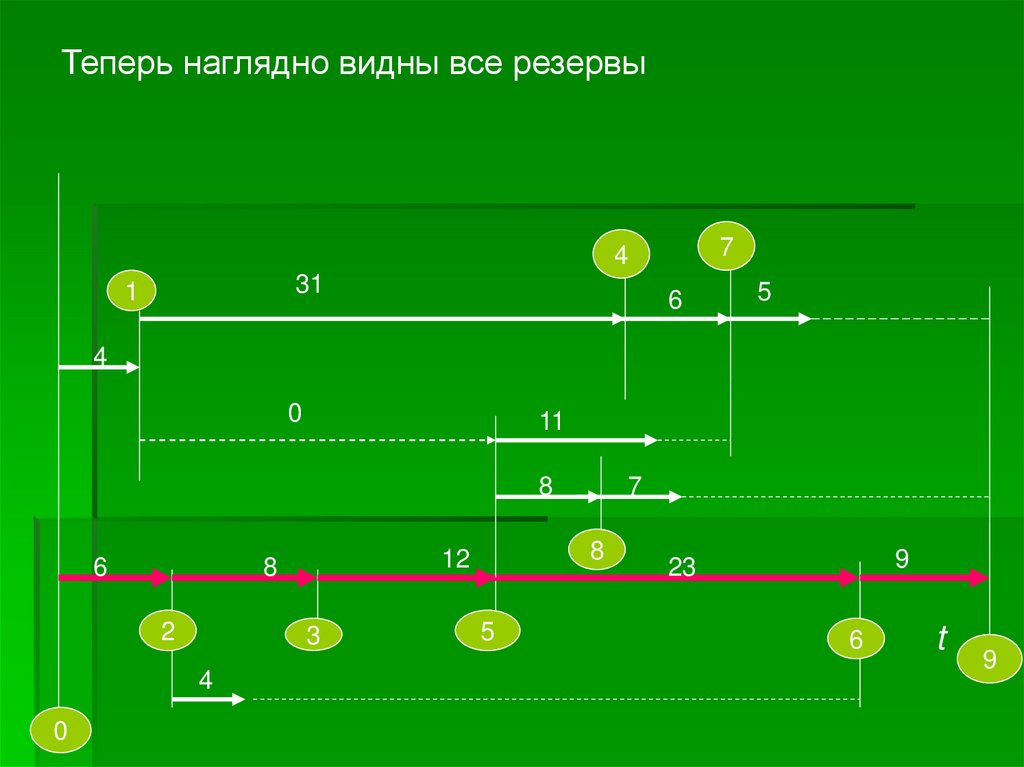
Теперь наглядно видны все резервы7
4
31
1
6
5
4
0
11
8
6
2
3
4
0
8
12
8
7
5
9
23
6
t
9
12.
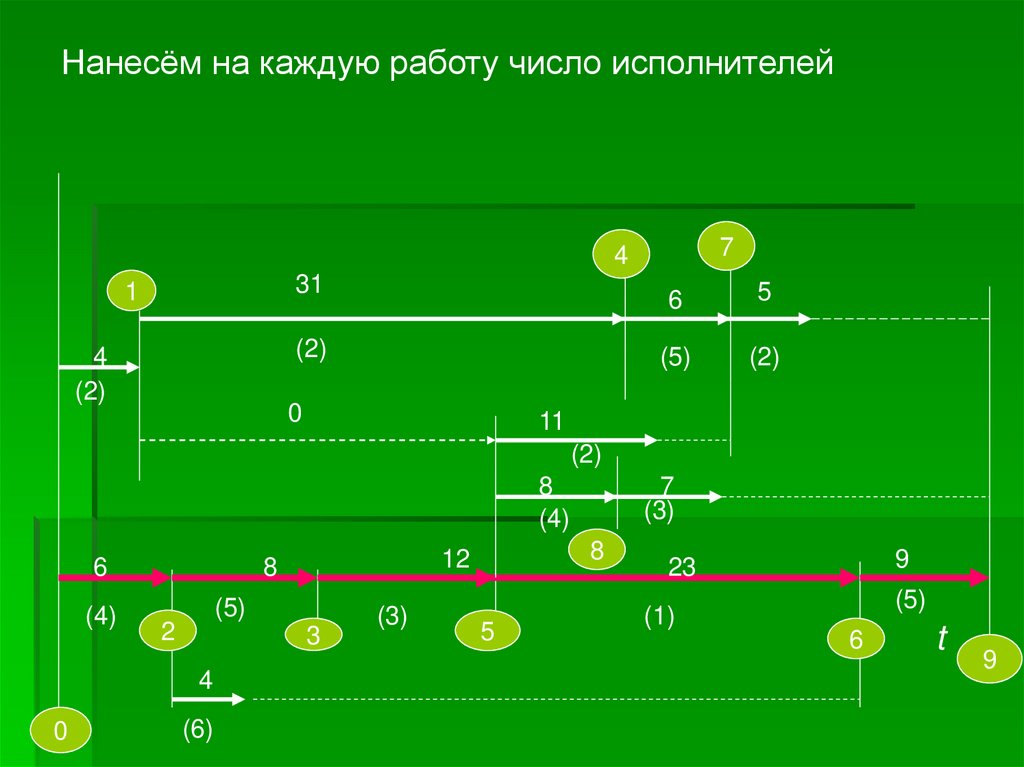
Нанесём на каждую работу число исполнителей7
4
31
1
(2)
4
(2)
0
6
5
(5)
(2)
11
(2)
8
(4)
6
(4)
(5)
2
3
4
0
(6)
8
12
8
(3)
7
(3)
5
9
23
(5)
(1)
6
t
9
13.
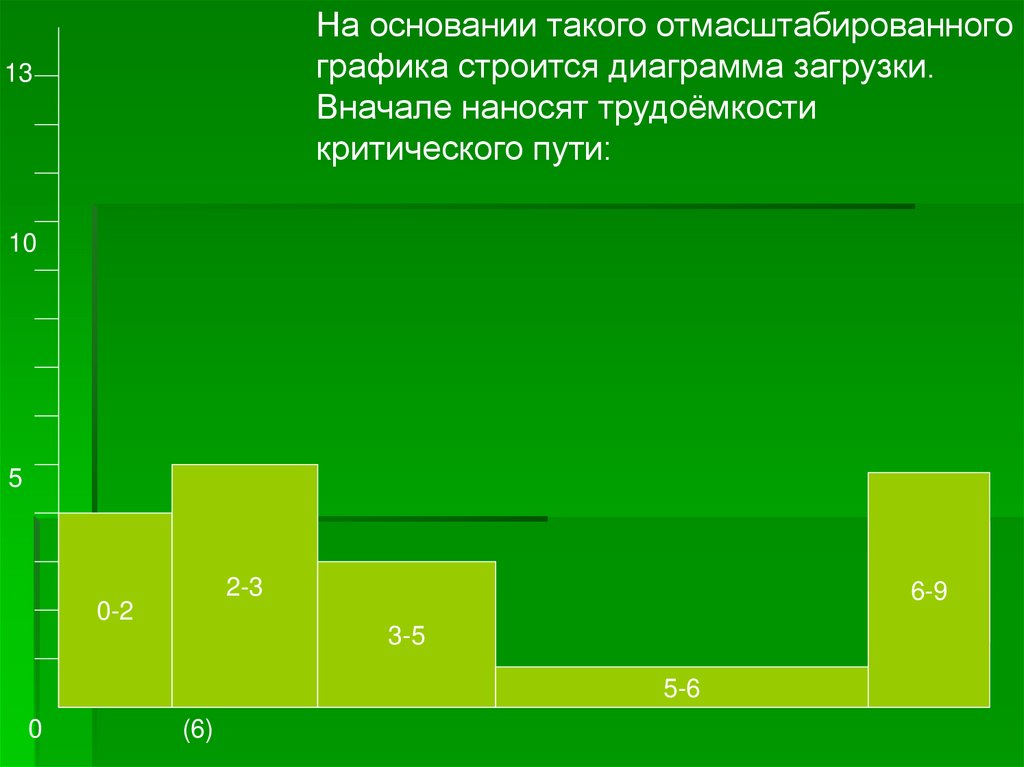
На основании такого отмасштабированногографика строится диаграмма загрузки.
Вначале наносят трудоёмкости
критического пути:
13
10
5
2-3
6-9
0-2
t
3-5
5-6
0
(6)
14.
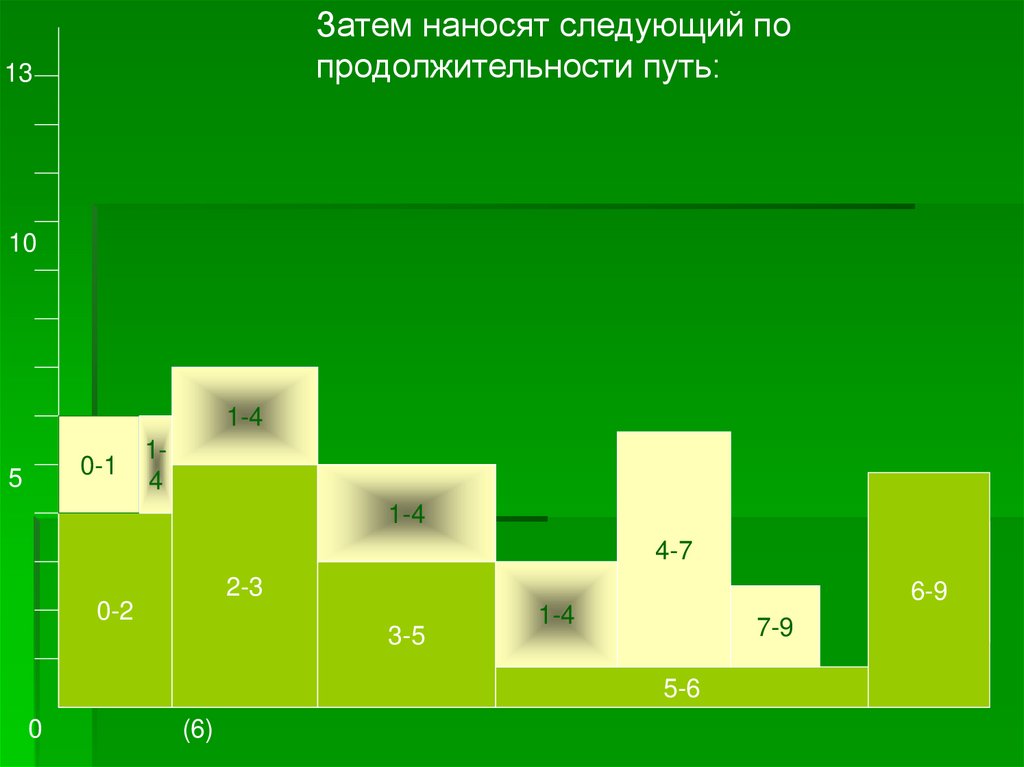
Затем наносят следующий попродолжительности путь:
13
10
1-4
0-1
5
14
1-4
4-7
2-3
6-9
0-2
3-5
1-4
7-9
5-6
0
(6)
t
15.
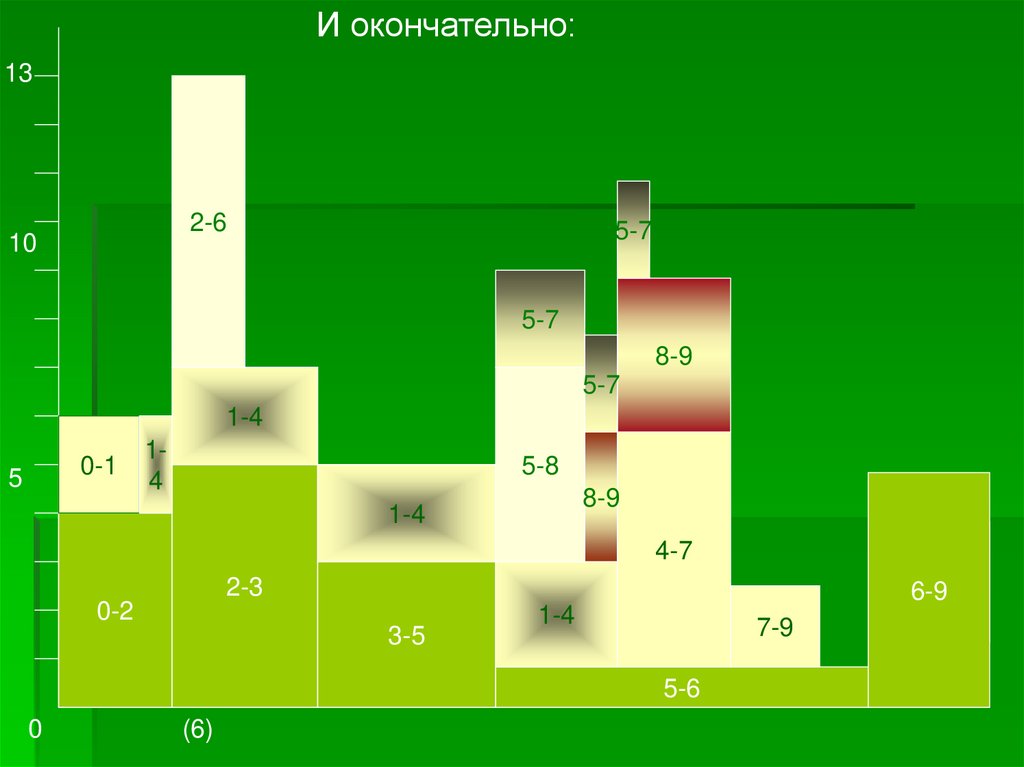
И окончательно:13
2-6
10
5-7
5-7
8-9
5-7
1-4
0-1
5
14
5-8
8-9
1-4
4-7
2-3
6-9
0-2
3-5
1-4
7-9
5-6
0
(6)
t
16. Оптимизацию сетевой модели можно осуществить по:
трудовым ресурсам,времени,
и времени, и трудовым ресурсам.
Рассмотрим оптимизацию по трудовым
ресурсам – минимизируем число
исполнителей.
17.
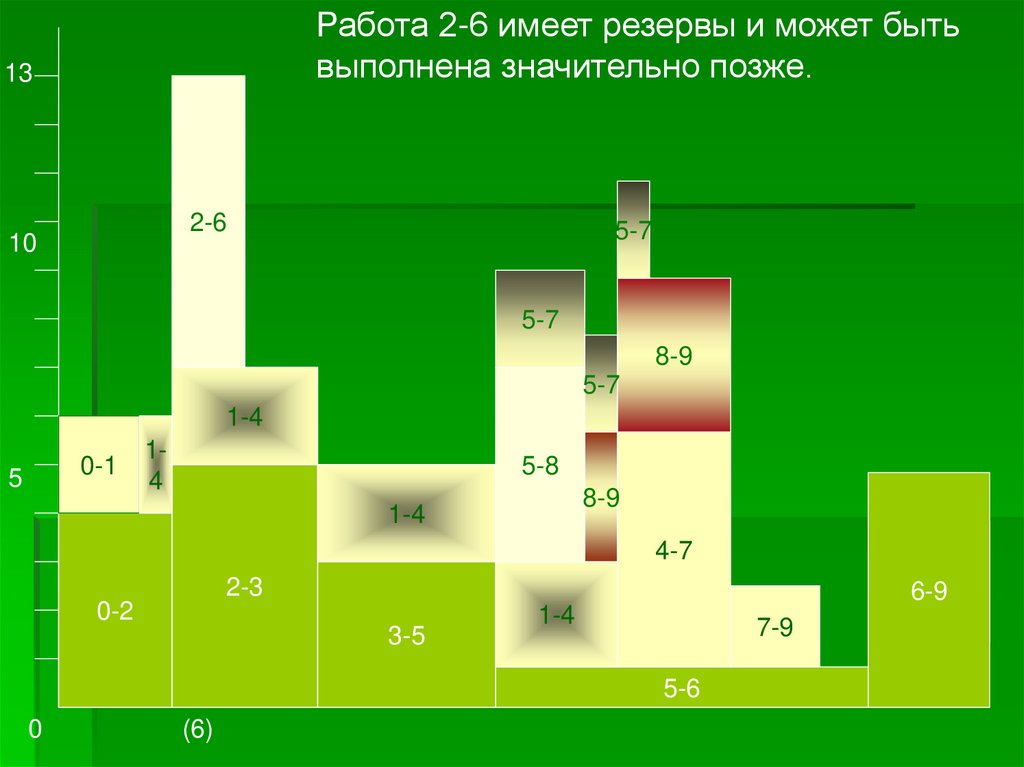
Работа 2-6 имеет резервы и может бытьвыполнена значительно позже.
13
2-6
10
5-7
5-7
8-9
5-7
1-4
0-1
5
14
5-8
8-9
1-4
4-7
2-3
6-9
0-2
3-5
1-4
7-9
5-6
0
(6)
t
18.
Вместо 13 мы можем привлечь 11 человек.Работа 8-9 также может быть начата
позже.
13
5-7
10
5-7
8-9
5-7
1-4
0-1
5
14
2-6
5-8
8-9
1-4
4-7
2-3
6-9
0-2
3-5
1-4
7-9
5-6
0
(6)
2-6
t
19.
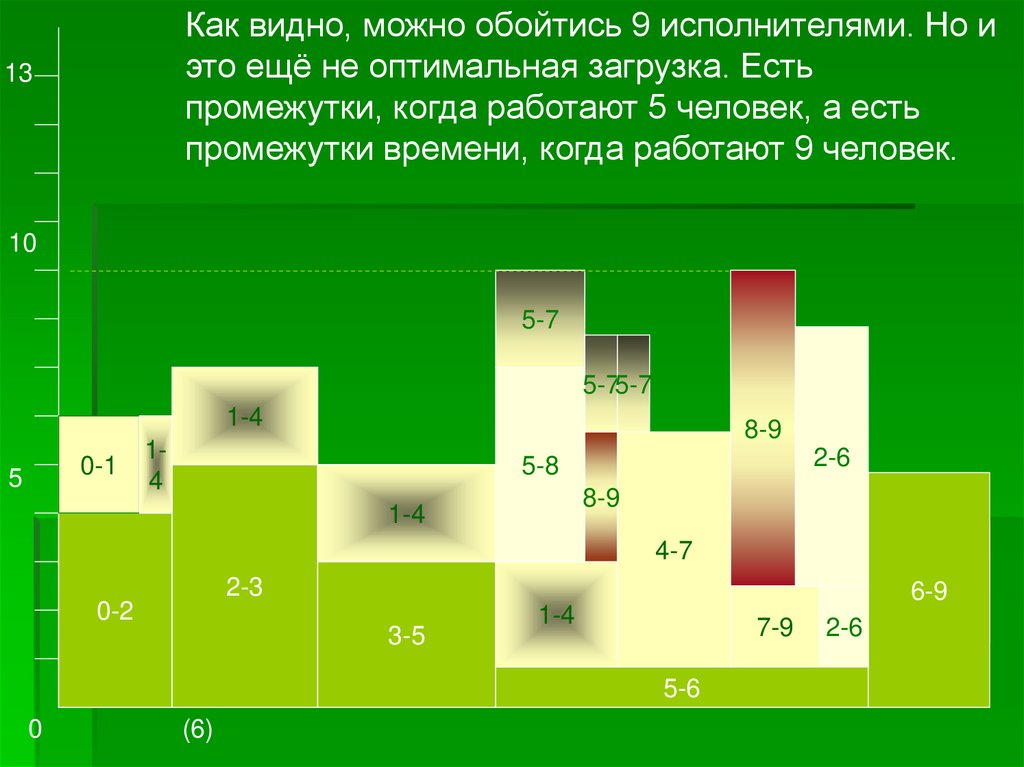
Как видно, можно обойтись 9 исполнителями. Но иэто ещё не оптимальная загрузка. Есть
промежутки, когда работают 5 человек, а есть
промежутки времени, когда работают 9 человек.
13
10
5-7
5-75-7
1-4
0-1
5
8-9
14
2-6
5-8
8-9
1-4
4-7
2-3
6-9
0-2
3-5
1-4
7-9
5-6
0
(6)
2-6
t
20.
Можно начать работу 5-7 позже:13
10
5-7
1-4
0-1
5
8-9
14
2-6
5-8
8-9
1-4
4-7
2-3
6-9
0-2
3-5
1-4
7-9
5-6
0
(6)
2-6
t
21.
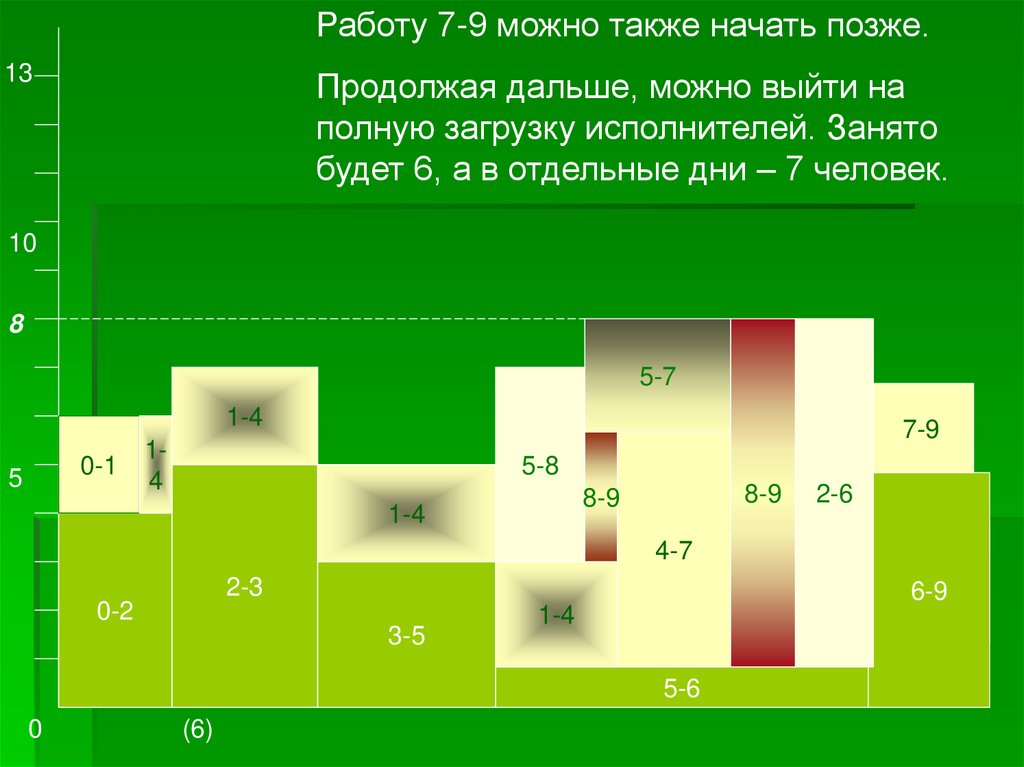
Работу 7-9 можно также начать позже.13
Продолжая дальше, можно выйти на
полную загрузку исполнителей. Занято
будет 6, а в отдельные дни – 7 человек.
10
8
5-7
1-4
0-1
5
7-9
14
5-8
8-9
8-9
1-4
2-6
4-7
2-3
6-9
0-2
3-5
1-4
t
5-6
0
(6)
22.
В результате оптимизации сетевой моделиоказывается, что к работе следует
привлечь не 13, а 7 человек.
Задача оптимизации значительно
усложняется, если к работе привлекаются
исполнители разной квалификации,
например, наладкой оборудования
одновременно занимаются рабочий,
инженер и электрик.
В таком случае для оптимизации следует
использовать автоматизированные
алгоритмы
22






 informatics
informatics








