Similar presentations:
Площадь
1.
Геометрия 9 класс.Повторение. Подготовка к
ГИА.
2. Тема урока: площадь.
Цели урока:• Систематизировать и обобщить знания
учащихся.
• Проверить уровень усвоения темы.
• Формировать умения применять знания к
решению задач.
3. Повторим теорию .
Запишем опорный конспект4. Формулы площадей четырёхугольников
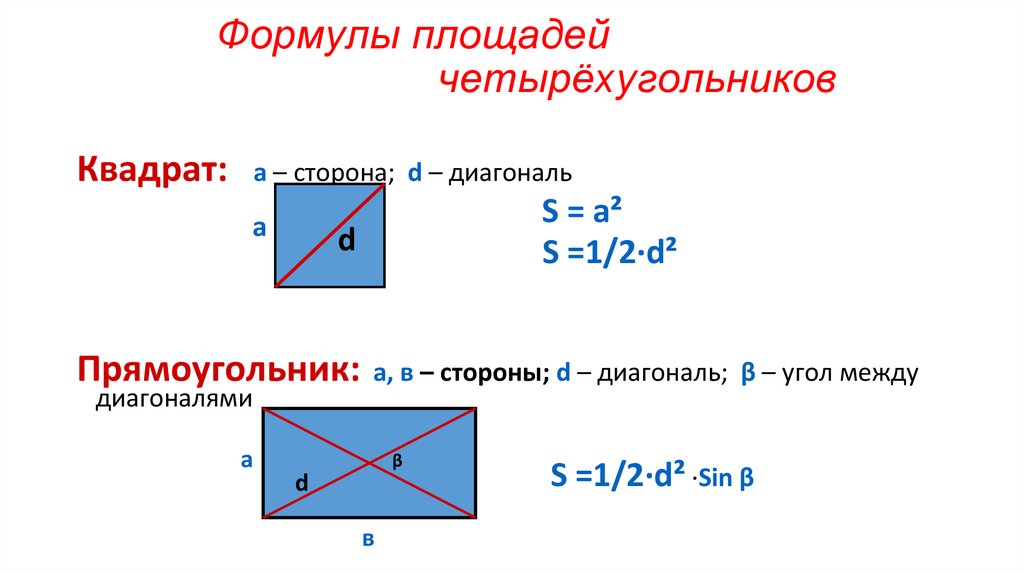
Квадрат:а – сторона; d – диагональ
а
d
Прямоугольник:
диагоналями
а
S = a²
S =1/2·d²
а, в – стороны; d – диагональ; β – угол между
S = a·в
β
d
в
S =1/2·d² ·Sin β
5. Формулы площадей четырёхугольников
Параллелограмм: а, в – стороны;α – угол между сторонами; d1 и d2 –
диагонали; β – угол между диагоналями; ha
и hв - высоты, проведенные к сторонам а и в
соответственно
в
а
α
hв
ha
S = a·ha = в·hв
S = a·в·Sinα
S =1/2·d1d2 ·Sin β
6. Формулы площадей четырёхугольников
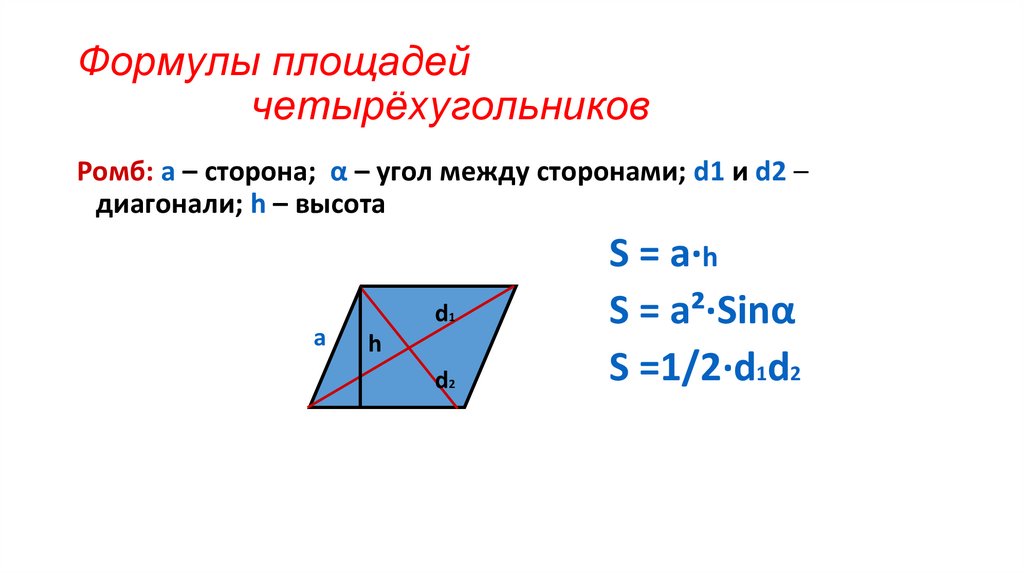
Ромб: а – сторона; α – угол между сторонами; d1 и d2 –диагонали; h – высота
а
d1
h
d2
S = a·h
S = a²·Sinα
S =1/2·d1d2
7. Формулы площадей четырёхугольников
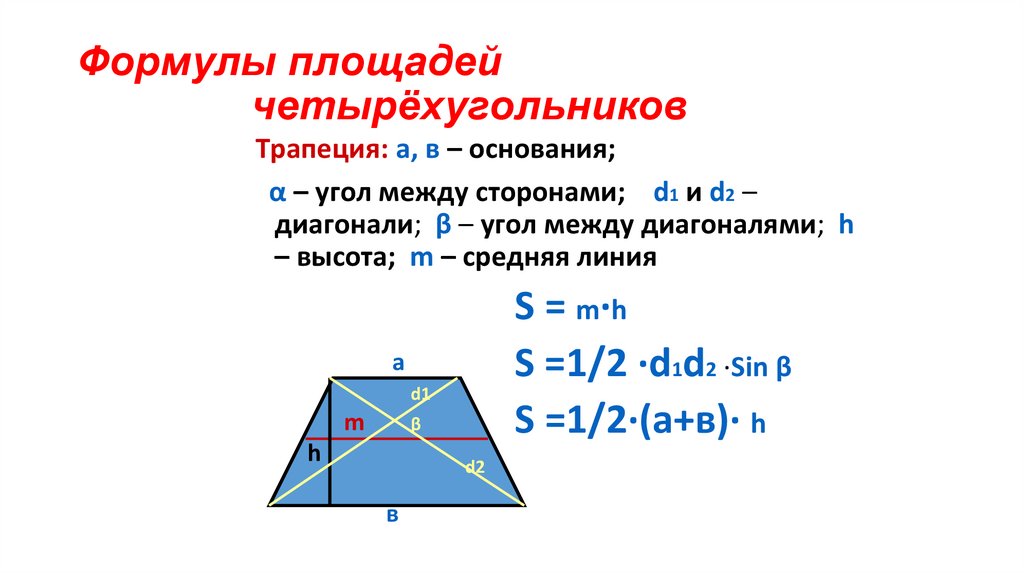
Трапеция: а, в – основания;α – угол между сторонами; d1 и d2 –
диагонали; β – угол между диагоналями; h
– высота; m – средняя линия
S = m·h
S =1/2 ·d1d2 ·Sin β
S =1/2·(а+в)· h
а
d1
m
β
h
d2
в
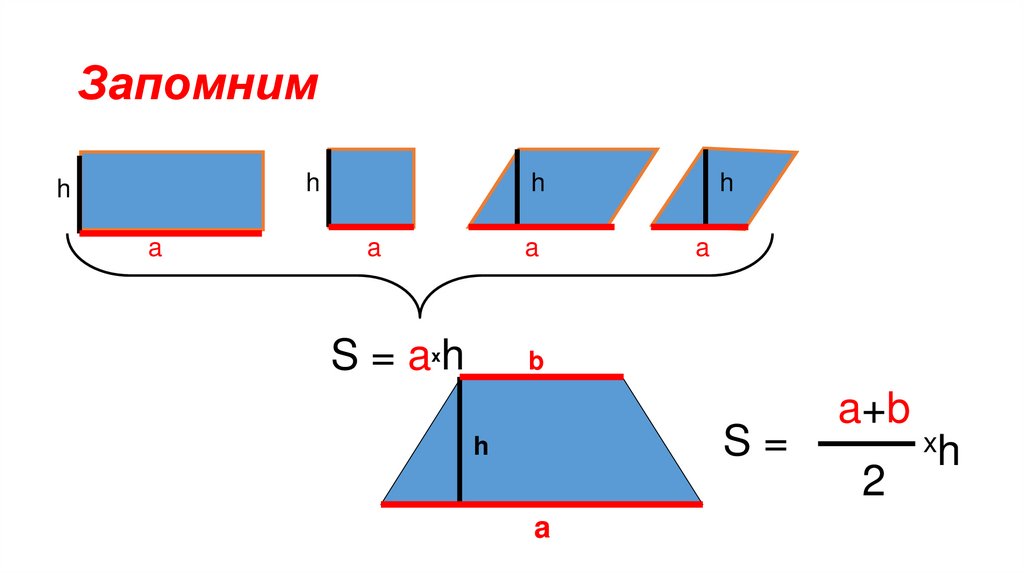
8. Запомним
hh
a
h
a
a
S=ah
x
h
a
b
S=
h
a+b
2
a
xh
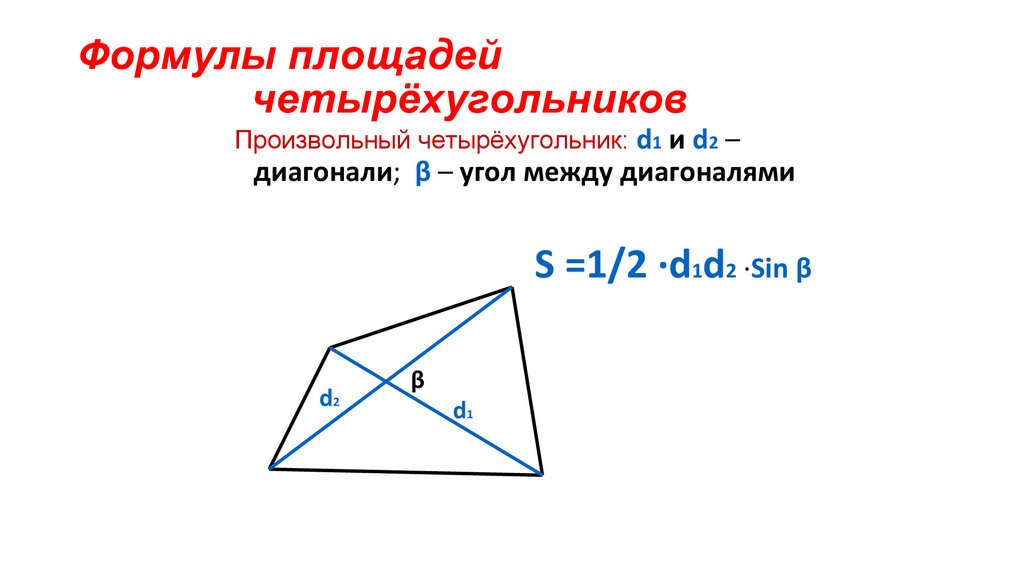
9. Формулы площадей четырёхугольников
Произвольный четырёхугольник: d1 и d2 –диагонали; β – угол между диагоналями
S =1/2 ·d1d2 ·Sin β
d2
β
d1
10. Формулы площадей треугольника
S= ab, где а, в - катеты прямоугольного треугольникаS=
S=
ah, где а - основание треугольника, h- высота
р- полупериметр, а, в, с- стороны
треугольника
11.
Площадь треугольника равна половинепроизведения двух его сторон на синус угла
между ними
S= absinC
12. Площадь круга и кругового сектора.
1) Площадь круга2) Площадь кругового сектора,
ограниченного дугой в 10
3) Площадь кругового сектора,
ограниченного дугой в α0
S = πR2
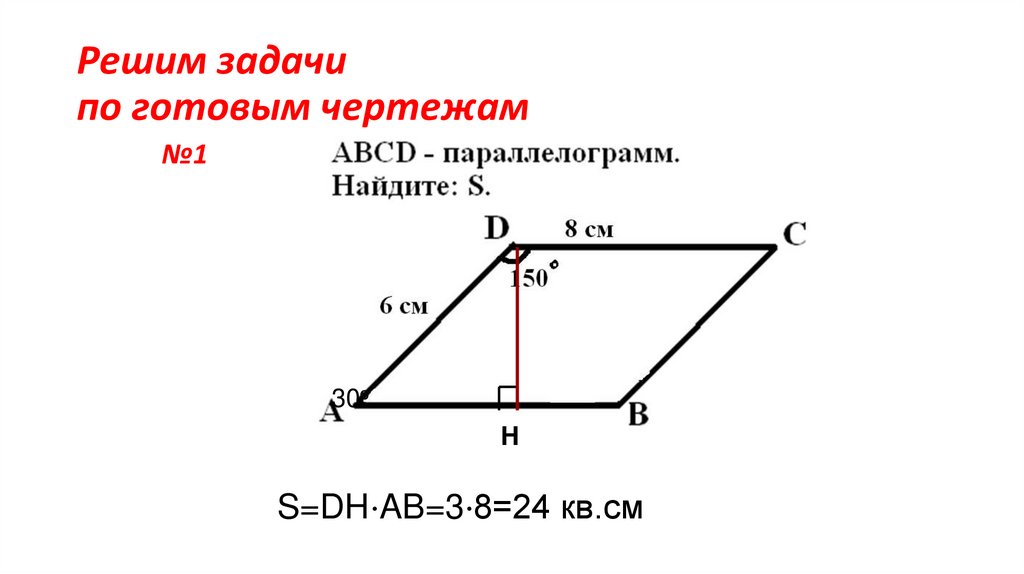
13. Решим задачи по готовым чертежам
№130o
H
S=DH⋅AB=3⋅8=24 кв.см
14. Решим задачи по готовым чертежам
№2S=32⋅2=64 кв.см
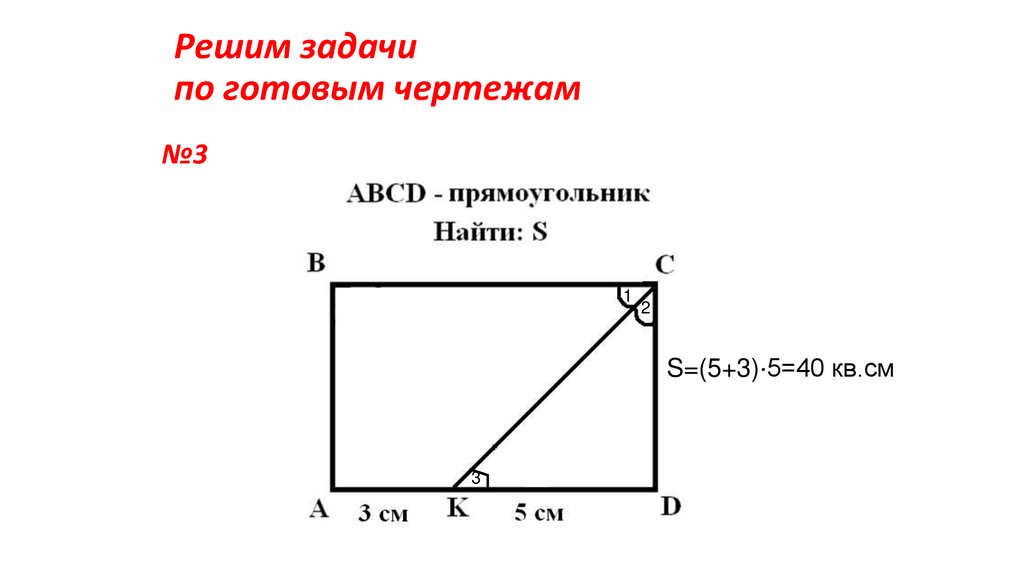
15. Решим задачи по готовым чертежам
№31
2
S=(5+3)⋅5=40 кв.см
30o
H
3
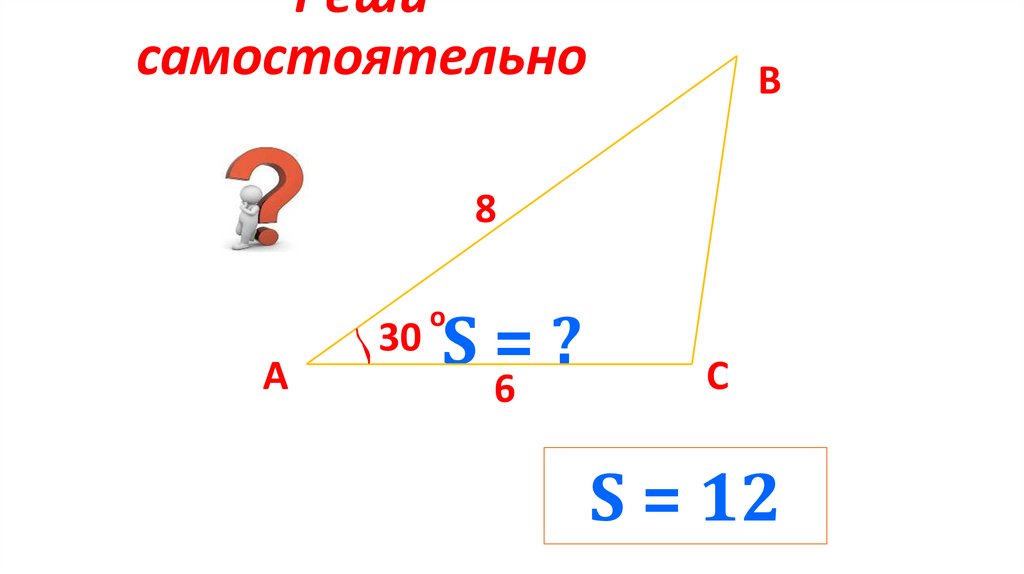
16. Реши самостоятельно
В8
А
30
S=?
о
6
С
S = 12
17.
Задания для самоподготовки1. Периметр параллелограмма равен 32 см. Найдите площадь
параллелограмма, если один из его углов на 60о больше прямого, а
одна из сторон равна 6 см.
2. Высота трапеции в 3 раза меньше одного из оснований и в 5 раз
меньше другого. Найдите основания и высоту трапеции, если ей
площадь равна 100 см2.
18. Ответы
№130 см.кв., 50 см.кв
№2
15 см , 25 см, 5 см










 mathematics
mathematics








