Similar presentations:
Проектирование алгоритмов. Сортировка методом «Грубой силы». Задача про Коммивояжёра (лекция 10)
1.
ПРОЕКТИРОВАНИЕ АЛГОРИТМОВAlgorithm Design
Лекция 10
Сортировка методом
«Грубой силы». Задача про
Коммивояжёра.
2.
План:1. Определение.
2.Немного истории
3.Применение алгоритма
4.Алгоритмы построения
3.
Ключевые слова:алгоритм,
свойства
алгоритма:
дискретность,
детерминированность,
понятность, результативность, конечность,
массовость,
исполнитель
алгоритма,
сложность алгоритма
ПРОЕКТИРОВАНИЕ АЛГОРИТМОВ
Algorithm Design
4. Метод грубой силы
5.
6.
7.
• Пример сортировки методом «грубой силы»:сортировка выбором и пузырьком
28
-5
16
0
29
3
-4
56
8.
9. Исчерпывающий перебор
Исчерпывающий перебор - подход к комбинаторным задачам с позиции грубой силы.Он предполагает:
• генерацию всех возможных элементов из области определения задачи
• выбор тех из них, которые удовлетворяют ограничениям, накладываемым условием
задачи
• поиск нужного элемента (например, оптимизирующего значение целевой функции
задачи).
Примеры:
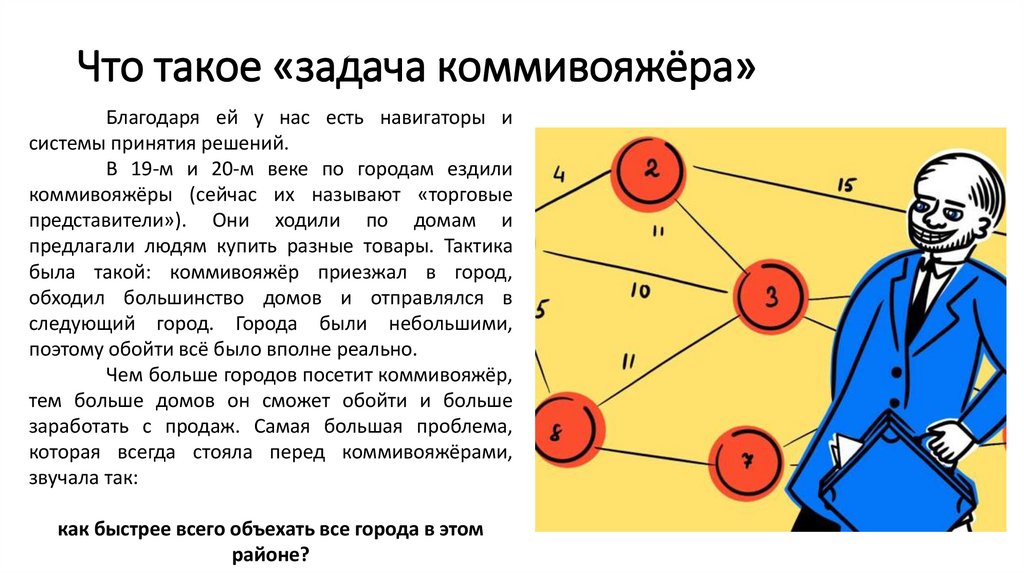
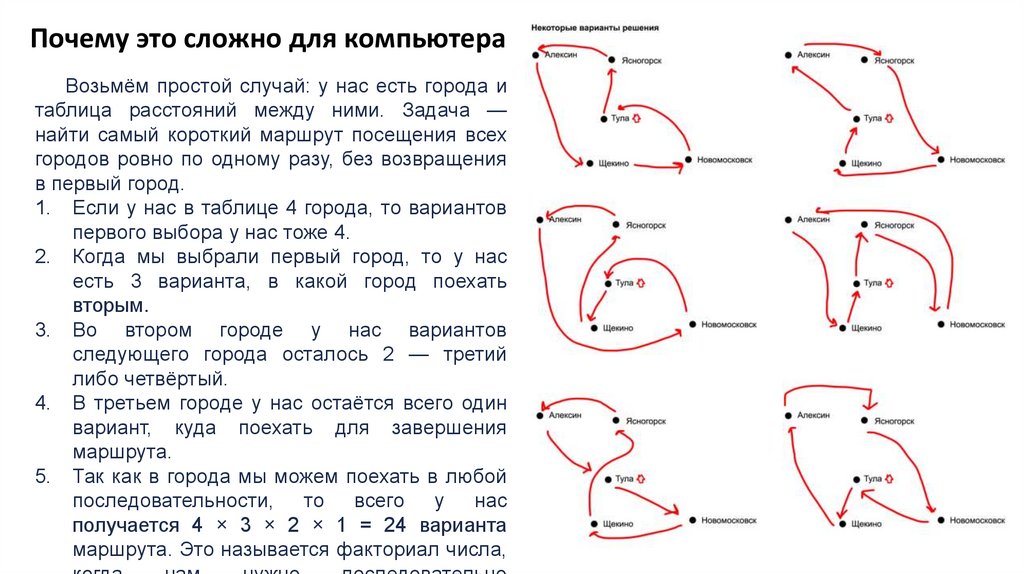
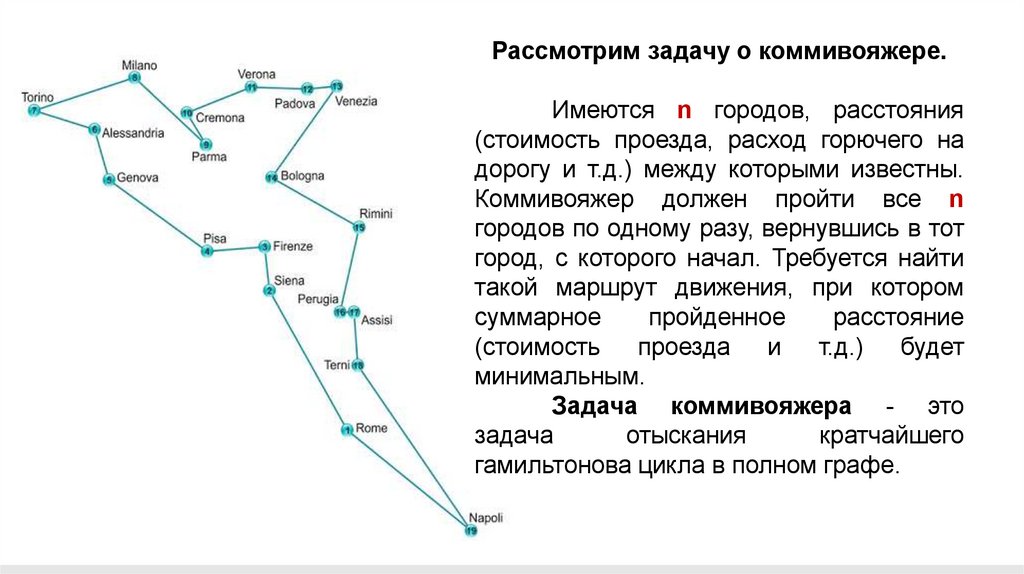
• Задача коммивояжера: найти кратчайший путь по заданным N городам, чтобы
каждый город посещался только один раз и конечным пунктом оказался исходный.
Рассмотреть все подмножества данного множества из n предметов,
• Задача
о рюкзаке:
N предметов
заданного
веса и стоимости
рюкзак,
вычислить
общийдано
вес каждого
из них
для выяснения
допустимости,
выдерживающий
вес W. Загрузить
рюкзак ссмаксимальной
стоимостью.
выбрать из допустимых
подмножества
максимальным
весом.
Это
- NP-сложные
задачи (не
известен алгоритм,
их за полиномиальное
Получить
все возможные
маршруты,
генерируярешающий
все перестановки
n—1
время).
промежуточных городов, вычисляя длину соответствующих путей и находя
кратчайший из них.
10. Эйлеровы графы
Работа Эйлера, датированная 1736 годом, положиланачало теории графов.
В этой работе Эйлер изложил теорию, позволившую
решить задачу о мостах Кенигсберга.
Перейдем к изложению задачи о кенигсбергских
мостах. Она состоит в следующем.
11. Эйлеровы графы
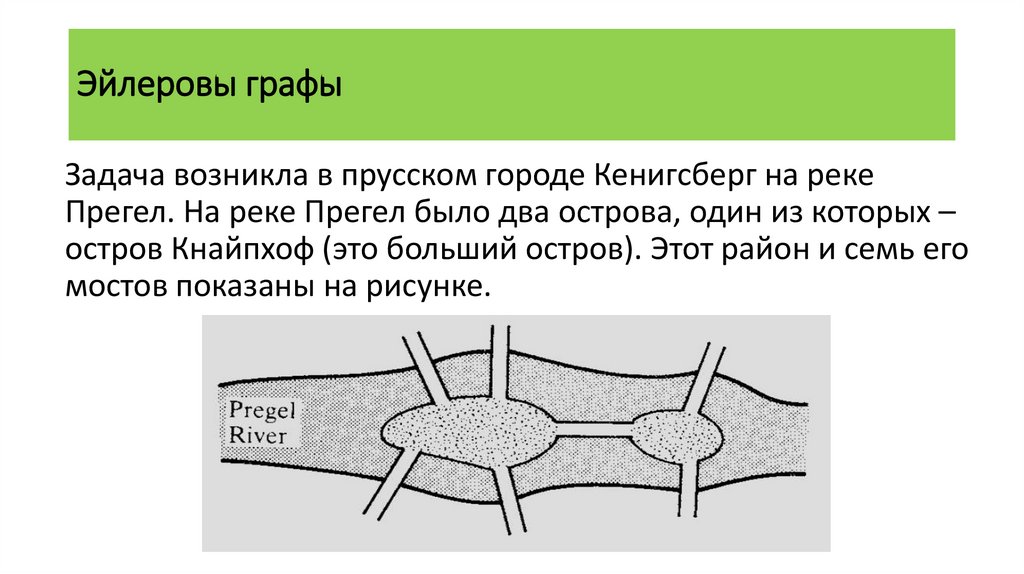
Задача возникла в прусском городе Кенигсберг на рекеПрегел. На реке Прегел было два острова, один из которых –
остров Кнайпхоф (это больший остров). Этот район и семь его
мостов показаны на рисунке.
12.
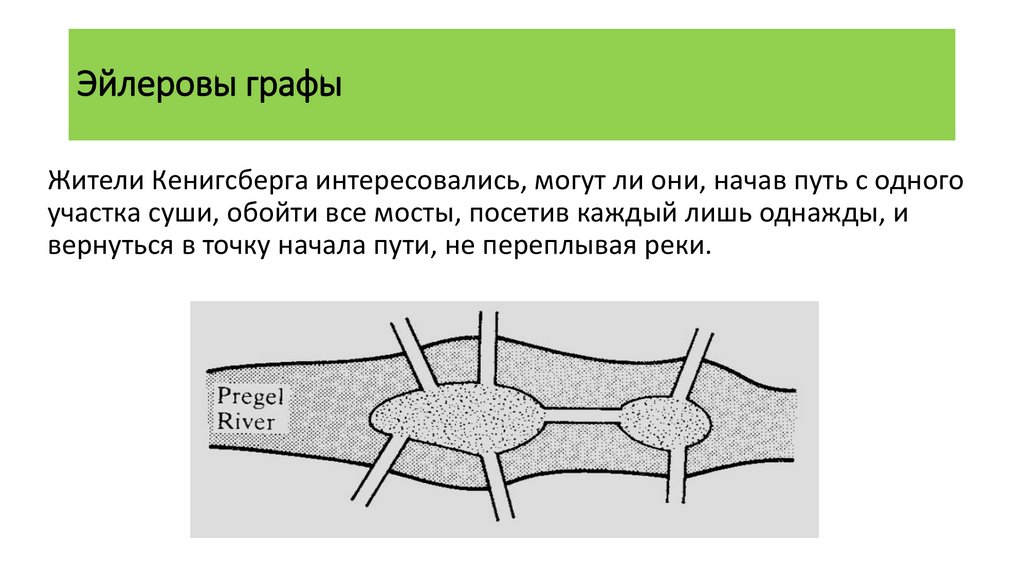
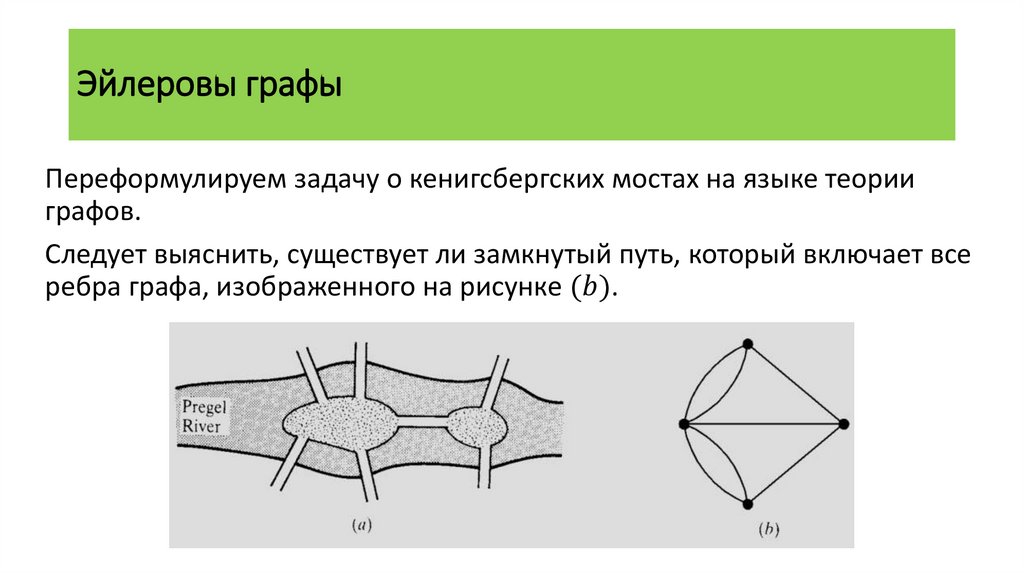
Эйлеровы графыЖители Кенигсберга интересовались, могут ли они, начав путь с одного
участка суши, обойти все мосты, посетив каждый лишь однажды, и
вернуться в точку начала пути, не переплывая реки.
13.
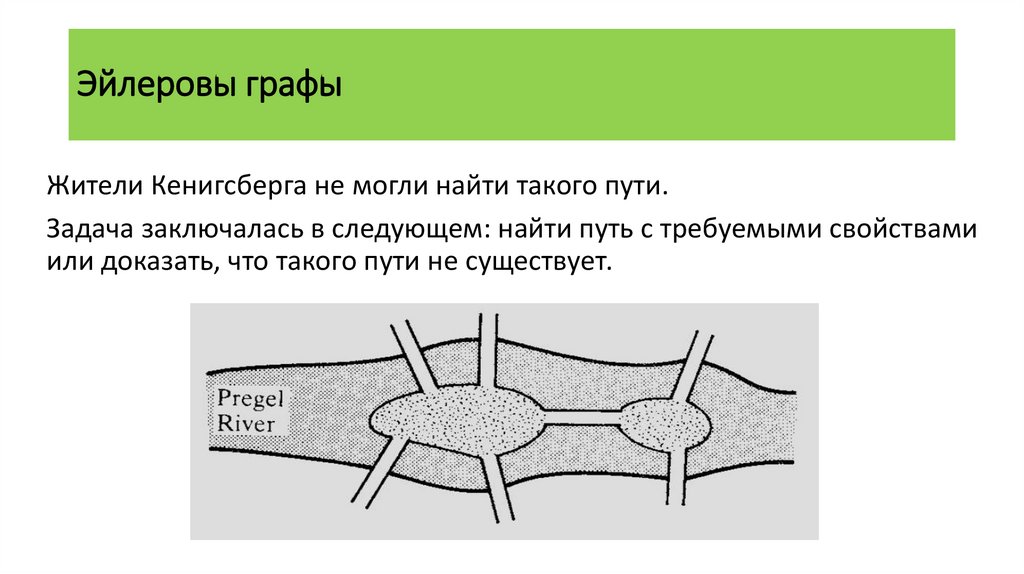
Эйлеровы графыЖители Кенигсберга не могли найти такого пути.
Задача заключалась в следующем: найти путь с требуемыми свойствами
или доказать, что такого пути не существует.
14.
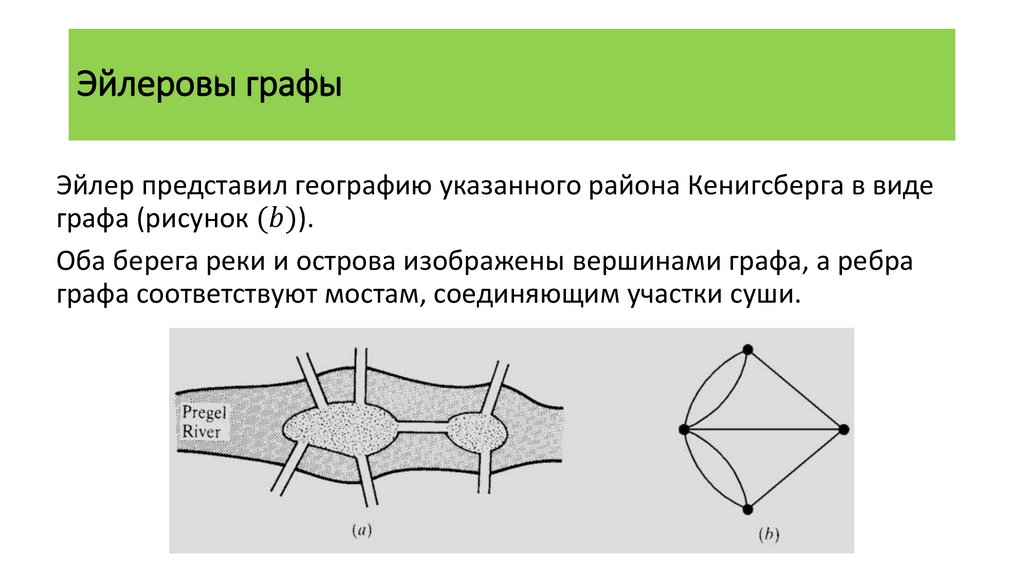
Эйлеровы графыЭйлер представил географию указанного района Кенигсберга в виде
графа (рисунок (
































 mathematics
mathematics








