Теория информации

1.

Теория информации
Лекции
Практика
ПОЛЕ
чисто
Весна 2022
1

2.

2

3.

Под информацией понимают:
- сведения, сообщения о чем-либо,
которыми обмениваются люди;
- сигналы, импульсы, образы,
циркулирующие в технических
(кибернетических) устройствах;
- количественную меру устранения
неопределенности (энтропии), меру
организации системы;
- отражение разнообразия в любых
объектах и процессах неживой и живой
природы.
Есть и другие ответы «что такое
информация?».
Многие ответы и определения
несовместимы друг с другом: информацией
именуются абстрактный концепт,
физическое свойство, функция
самоуправляемых систем; информация
объективна и субъективна, материальна и
идеальна, это и вещь, и свойство, и
отношение.
Информация проникла в терминологию
почти всех современных наук, и по этой
причине признается общенаучной
категорией.
Теория информации – область деятельности,
связанная с изучением процессов получения,
передачи, обработки и хранения информации
В теории информации изучаются:
• виды и формы представления информации;
• методы и средства определения количества
информации;
• принципы кодирования и декодирования
информации;
• способы передачи цифровой информации;
• методы повышения помехозащищенности
передачи и приема данных;
• основы теории сжатия данных.
3

4.

4

5.

Люди обмениваются
устными сообщениями,
записками, используют для
этого электронную и
голосовую почту. Все это –
информационные процессы.
Информационные
процессы - это процессы
передачи, хранения и
переработки информации.
5

6.

6

7.

7

8.

8

9.

9

10.

10

11.

11

12.

Информация (information) –
1. Совокупность сведений о
фактических данных и
зависимостях между ними;
сведения, являющиеся объектом
некоторых операций: передачи,
распределения, преобразования,
хранения или непосредственного
использования; сведения,
релевантные пользователю.
2. В вычислительной технике:
содержание, присваиваемое
данным посредством соглашений,
распространяющихся на эти
данные; данные, подлежащие
вводу в компьютер,
обрабатываемые на нем и
выдаваемые пользователю.
Законы, методы и способы
накопления, обработки и передачи
информации с помощью
компьютеров и иных технических
устройств изучаются
информатикой.
12

13.

13

14.

Теория информации – область
деятельности, связанная с изучением
процессов получения, передачи,
обработки и хранения информации
в теории информации изучаются:
• виды и формы представления
информации;
• методы и средства определения
количества информации;
• принципы кодирования и
декодирования информации;
• способы передачи цифровой
информации;
• методы повышения
помехозащищенности передачи и
приема данных;
• основы теории сжатия данных.
Теории информации
Структурная теория информации
рассматривает структуру построения
отдельных информационных сообщений.
Единица количества информации –
элементарная структурная единица квант.
Статистическая теория оценивает
информацию с точки зрения меры
неопределенности. Основное внимание
уделяется распределению вероятностей, либо
появлению сигналов, либо изменению
характеристик этих сигналов и построению на
его основе некоторых обобщенных
характеристик, позволяющих оценить
количество информации.
Семантическая теория занимается
изучением смысловых характеристик
информации: ценности, содержательности,
полезности. Помогает связать количество и
ценность информации с такими обобщенными
характеристиками системы, как
эффективность, информационная пропускная
способность, информационная
помехоустойчивость.
14

15.

Информация — это фундаментальное
ПОНЯТИЕ, его невозможно определить
однозначно
Используются не определением информации, а
ПОНЯТИЕ информации.
Понятия отличаются от определений тем, что не
даются однозначно, а вводятся на примерах
Термин информация происходит от латинского
informatio, что означает разъяснение,
осведомление, изложение. С позиции
материалистической философии информация
есть отражение реального мира с помощью
сведений (сообщений).
Сообщение - это форма представления
информации в виде речи, текста, изображения,
цифровых данных, графиков, таблиц и т.п. В
широком смысле информация - это
общенаучное понятие, включающее в себя
обмен сведениями между людьми, обмен
сигналами между живой и неживой природой,
людьми и устройствами.
Информация - это содержание сообщения,
сигнала, памяти.
Информация характеризует
разнообразие (неоднородность) в окружающем мире
Как получают информацию
Человек получает информацию через свои органы
чувств: глаза, уши, рот, нос и кожу. Поэтому в
зависимости от того, с помощью каких органов
чувств получается информация, ее можно разделить
на следующие виды:
зрительная информация (визуальная, от
англ. visual) — поступает через глаза (по
разным оценкам, это 80–90 % всей получаемой
нами информации);
звуковая информация (аудиальная, от англ. audio)
— поступает через уши;
вкусовая информация — поступает через язык;
обонятельная информация (запахи) — поступает
через нос;
тактильная информация — мы ее получаем с
помощью осязания (кожи), «на ощупь».
Существует информация, получаемая с помощью
«мышечного чувства» (человеческий мозг получает
импульсы от мышц и суставов при перемещении
частей тела).
Некоторые животные чувствуют магнитное поле
Земли и используют его для выбора направления
движения.
15

16.

Информация — это
сведения, обладающие
такими характеристиками, как
понятность, достоверность,
новизна и актуальность
(с точки зрения человека)
Информация — это снятая
неопределенность
(по К. Шеннону)
Информационный объем
сообщения — количество
двоичных символов, которое
используется для кодирования
этого сообщения.
За единицу измерения информации принят
1 бит (от англ. Binary digit)
Количество информации минимально возможное
количество двоичных знаков,
необходимых для кодирования
последовательности к
содержанию представленного
сообщения
(по А.Н. Колмогорову)
1 бит — это количество информации,
которое можно передать в сообщении,
состоящем из одного двоичного знака (0
или 1) — алфавитный подход
1 бит — это количество информации,
уменьшающее
неопределенность
знаний в два раза — содержательный
подход
1Кб (килобайт) = 210 байт = 1024 байт
1Мб (мегабайт) = 210 Кб = 1024 Кб
1Гб (гигабайт) = 210 Мб = 1024 Мб
1Тб (терабайт) = 210 Гб =1024 Гб
16

17.

17

18.

Человек, информация, знания
Обо всех изменениях в окружающем
мире человек узнает с помощью своих
органов чувств: сигналы от них
(«первичная» информация) поступают
в мозг. Чтобы понять эти сигналы
(извлечь информацию) человек
использует знания — свои
представления о природе, обществе,
самом себе.
Знания — это модель мира, которая
есть у человека. Получив информацию
(«поняв» сигналы, поступившие от
органов чувств), он корректирует эту
модель, дополняет свои знания.
Полученная информация не всегда
обогащает наши знания. Сообщение
увеличивает знания человека, если оно
понятно и содержит новые сведения.
Например, информация о том, что
2∙2=4
вряд ли увеличит ваши знания, потому
что вы это уже знаете, эта информация для
вас не нова.
Однако она будет новой для тех, кто
изучает таблицу умножения. Это значит,
что изменение знаний при получении
сообщения зависит от того, что человек
знал до этого момента. Если он знает все,
что было в полученном сообщении,
знания не изменяются.
Вместе с тем сообщение «Учет
вибронных взаимодействий
континуализирует моделирование
диссипативных структур» (или сообщение
на неизвестном языке) также не
увеличивает знания, потому что эта фраза,
скорее всего, вам непонятна. Иначе говоря,
имеющихся знаний не хватает для того,
чтобы воспринять новую информацию.
18

19.

Эти идеи послужили
основой семантической (смысловой)
теории информации.
На рисунке показано, как зависит
количество полученных знаний I от того,
какая доля информации q в сообщении уже
известна получателю.
«Измерить» смысл информации, оценить
его числом, сложно.
Для оценки количества информации
используются спец. подходы
Когда человек хочет поделиться с кемто своим знанием, он может сказать:
«Я знаю, что...»,
или
«Я знаю, как...».
Это говорит о том, что есть два разных
вида знаний.
В первом случае знания — это
некоторый известный факт, например: «Я
знаю, что Луна вращается вокруг Земли».
Такие знания
называются декларативными, человек
выражает их словами (декларирует).
Декларативные знания — это факты,
законы, принципы.
Второй тип знаний («Я знаю, как...»)
называют процедурными. Они выражаются
в том, что человек знает, как нужно
действовать в той или иной ситуации.
К процедурным знаниям относятся
алгоритмы решения различных задач.
19

20.

Чтобы сохранить знания и передать
другим людям, нужно выразить их на
каком-то языке (например, рассказать,
записать, нарисовать и т. п.). Только
после этого их можно хранить,
обрабатывать, передавать, причем с этим
может справиться и компьютер.
Информацию, зафиксированную
(закодированную) в какой-то форме,
называют данными, имея в виду, что
компьютер может выполнять с ними
какие-то операции, но не способен
понимать смысл.
Чтобы данные стали информацией, их
нужно понять и осмыслить, а на это
способен только человек. Если человек,
получающий сообщение, знает язык, на
котором оно записано, он может понять
смысл этого сообщения, то есть получить
информацию.
Обрабатывая и упорядочивая
информацию, человек выявляет
закономерности — получает знания.
Существуют достаточно различия
между понятиями «данные»,
«информация», «знания».
На практике чаще всего все это
называется общим термином
«информация».
20

21.

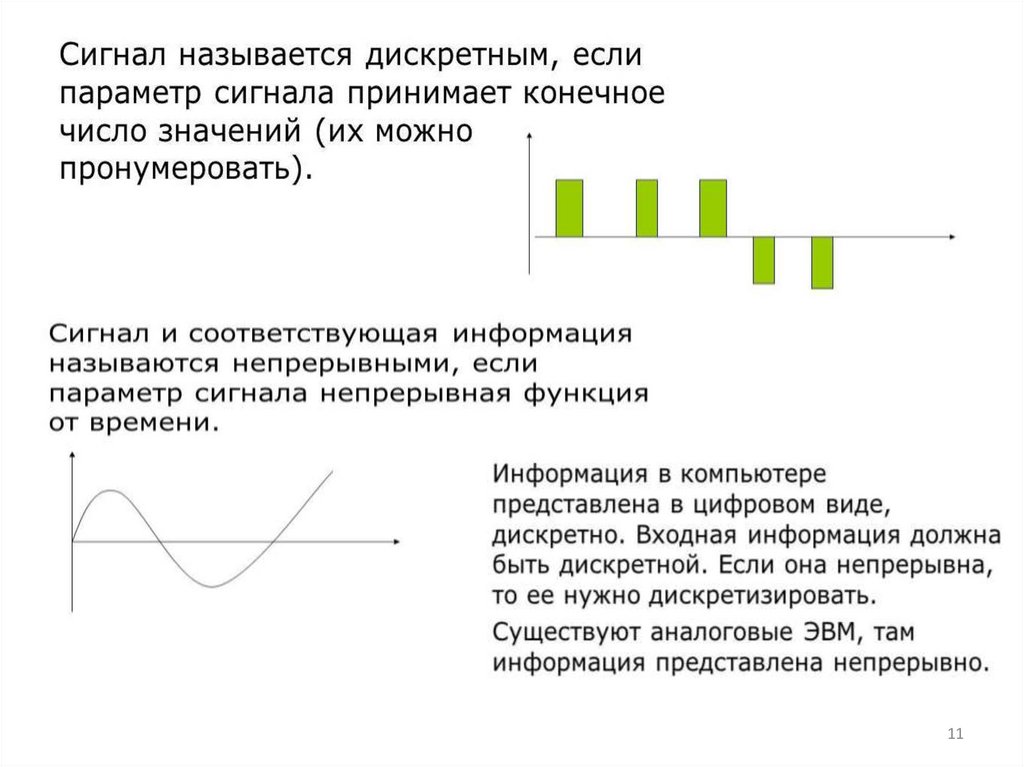
Виды информации
Числовая представляется
цифрами и отражает
результаты некоторого
вычисления.
Текстовая представлена в
виде слов, состоящих из
символов.
Кодовая представлена кодами
(напр., азбука Морзе,
машинные коды и т п.).
Графическая представлена
графическими объектами с
учетом их
геометрических и оптических
свойств.
Акустическая представлена
звуками.
Телевизионная - это
изображения в ТВ-формате.
Видео-информация - это
видео- и кинофильмы с
специальных форматах
Формы представления информации
Информация может быть представлена
(зафиксирована, закодирована) в различных формах:
текстовая информация — последовательность
символов (букв, цифр, других знаков); в тексте
важен порядок их расположения, например,
КОТ и ТОК — два разных текста, хотя они
состоят из одинаковых символов;
числовая информация;
графическая информация (рисунки, картины,
чертежи, карты, схемы, фотографии и т. п.);
звуковая информация (звучание голоса, мелодии,
шум, стук, шорох и т. п.);
мультимедийная информация объединяет
несколько форм представления информации
(например, видеоинформация).
Одна и та же информация может быть
представлена по-разному.
Например, результаты измерения температуры в
течение недели можно сохранить в виде текста,
чисел, таблицы, диаграммы, и т. д.
21

22.

22

23.

23

24.

24

25.

25

26.

26

27.

27

28.

Свойства информации
Понятие «информация» используется многими
научными дисциплинами, имеет большое
количество разнообразных свойств, но каждая
дисциплина обращает внимание на те свойства
информации, которые для нее наиболее важны.
Рассмотрим следующие свойства информации:
Дуализм информации характеризует
ее двойственность.
С одной стороны, информация объективна в
силу объективности данных, с другой —
субъективно, в силу субъективности
применяемых методов. Иными словами,
методы могут вносить в большей или
меньшей степени субъективный фактор и
таким образом влиять на информацию в
целом.
Например, два человека читают одну и ту же
книгу и получают подчас весьма разную
информацию, хотя прочитанный текст, то
есть данные, были одинаковы.
Более объективная информация применяет
методы с меньшим субъективным
элементом.
1.
Полнота информации характеризует
степень достаточности данных для принятия
решения или создания новых данных на
основе имеющихся. Неполный набор
данных оставляет большую долю
неопределенности, то есть большое число
вариантов выбора, а это потребует
применения дополнительных методов,
например, экспертных оценок, бросание
жребия и т. п. Избыточный набор данных
затрудняет доступ к нужным данным,
создает повышенный информационный
шум, что также вызывает необходимость
дополнительных методов, например,
фильтрацию, сортировку. И неполный, и
избыточный наборы затрудняют получение
информации и принятие адекватного
решения.
3.
Достоверность информации — это
свойства, характеризующее степень
соответствия информации реальному
объекту с необходимой точностью. При
работе с неполным набором данных
достоверность информации может
характеризоваться вероятностью: например,
можно сказать, что при бросании монеты с
28
вероятностью 50 % выпадет герб.
2.

29.

Адекватность информации выражает
степень соответствия создаваемого с помощью
информации образа реальному объекту,
процессу, явлению. Полная адекватность
достигается редко, так как обычно приходится
работать с не самым полным набором данных, то
есть присутствует неопределенность,
затрудняющая принятие адекватного решения.
Получение адекватной информации также
затрудняется при недоступности адекватных
методов.
5.
Доступность информации — это
возможность получения информации при
необходимости. Доступность складывается из
двух составляющих: из доступности данных и
доступности методов. Отсутствие хотя бы
одного из них дает неадекватную информацию.
6.
Актуальность информации. Информация
существует во времени, так как все
информационные процессы существуют во
времени. Информация, актуальная сегодня,
может стать совершенно ненужной по истечении
некоторого времени. Например, программа
телепередач на эту неделю будет неактуальна
для телезрителей на следующей неделе.
4.
29

30.

30

31.

31

32.

Используются не определением информации, а
ПОНЯТИЕ информации.
Понятия отличаются от определений тем, что не
даются однозначно, а вводятся на примерах
Наиболее распространены следующие определения информации.
«Информация – это данные и методы их обрабатывающие».
Информация – это продукт взаимодействия данных и адекватных
им методов преобразования данных.
Информация возникает именно в тот момент, когда данные
начинают обрабатываться. Причём в зависимости от конкретного
способа обработки из исходных данных может быть получена
совершенно разная информация. Одни и те же пять цифр могут быть
как размером зарплаты, так и кодом запуска стратегических ракет.
Содержание этой общенаучной категории - в виде
следующих теорий или концепций:
32

33.

33

34.

Математическая теория
информации (ТИ)
Трактует информацию в качестве абстрактного
понятия.
Норберт Винер - «информация есть
информация, а не материя и не энергия».
Из определения вытекает, что информация —
не существующий реально объект, а
умственная абстракция, созданная
человеческим разумом.
В этом же смысле понятие информации
используется в теории коммуникации,
развитой в конце 1940-х гг. американским
математиком Клодом Шенноном.
В этой теории понятие информации служит
для решения практических задач, с которыми
сталкиваются инженеры-связисты:
- оптимизация кодирования сообщений,
повышение помехоустойчивости,
- распознавание сигналов на фоне шумов,
- расчет пропускной способности каналов
связи и т.п.
Каждому сигналу или их ансамблю (например,
букве или слову), которые передаются по
коммуникационному каналу, на основе
известных статистических частот приписывалась
априорная вероятность их появления.
Считалось, что чем менее вероятно (т.е. чем
более неожиданно), появление того или иного
сигнала, тем больше информации для
потребителя несет этот сигнал. Можно найти
содержательные основания для подобной
трактовки в обыденном понимании
информации как новости или известия.
Удобство вероятностно-статистического
представления коммуникационной
деятельности состоит в том, что можно ввести
количественную меру для оценки степени
«неожиданности» сообщения. В простейшем
случае формула информации К. Шеннона имеет
следующий вид:
где I — количество информации, pi —
вероятность появления i-го сигнала, n —
количество возможных сигналов.
34

35.

Если сигналов всего два и они равновероятны, то
формула принимает вид:
В случае двоичных логарифмов log 1/2 = -1,
а I = 1. Это значение принято в теории Шеннона в
качестве единицы измерения информации и
называется бит.
Отсюда проистекает понимание информации как
снятой неопределенности или как результата
выбора из возможных альтернатив.
Есть другие математические концепции, не
связывающие информацию с вероятностью.
Например, в алгоритмической теории информации
А.Н. Колмогорова информация – это длина
алгоритма, позволяющего преобразовать один
объект в другой, т.е. информация — это мера
сложности объекта.
Ограниченность математических теорий
информации заключается в том, что они полностью
абстрагируются от осмысленности и ценности
информации для потребителя. Критика данного
подхода связана с тем, что в математических
теориях понятие информации не связано ни с
формой, ни с содержанием сообщений (сигналов),
передаваемых по каналу связи.
Получается, что «совокупность 100
букв, выбранных 13 случайным
образом, фраза в 100 букв из газеты,
из пьесы Шекспира или теоремы
Эйнштейна имеют в точности
одинаковое количество
информации».
Итак, согласно математической
теории, информация, точнее
количество информации, есть
абстрактная фикция, умственный
конструкт; она не существует в
физической реальности, как не
существуют логарифмы или мнимые
числа.
Примеры:
35

36.

Методы и модели оценки количества
информации
Для теоретической информатики информация
играет такую же роль, как и вещество в физике.
Для характеристик информации используются
единицы измерения, что позволяет некоторой
порции информаии приписывать числа –
количественные характеристики информации. На
сегодняшний день наиболее известны
следующие способы измерения количества
информации (меры количества информации):
• структурные (объёмные);
• энтропийный;
• алгоритмический
Структурные меры информации
Ряд авторов называют их объёмными. При их
использовании учитывается только количество
информационных элементов, содержащихся в
информации, связей между ними или
комбинаций из них. Под информационными
элементами понимаются неделимые части
информации (кванты) в дискретных моделях
реальных информационных комплексов, а также
элементы алфавитов в числовых системах. В
структурной мере различаются геометрическая,
комбинаторная и аддитивная меры информации.
Определение количества информации
геометрической мерой
сводится к измерению площади или
объёма геометрической модели данного
информационного комплекса в
количестве дискретных единиц.
Например, при рассмотрении
характеристик визуализаторов указывают
количество пикселей, которое может
формироваться в строке (разрешение по
горизонтали), количество строк, которое
может формироваться по вертикали
(разрешение по вертикали), глубину
цвета пикселя (количество цветовых
оттенков, которое может принимать
пиксель). Геометрической мерой
определяется максимально возможное
количество информации, которое можно
представить данной структурой.
36

37.

Количество информации в комбинаторной
мере вычисляется как количество
комбинаций элементов информационных
комплексов. Для подсчета можно
использовать формулы комбинаторики
(число сочетаний, перестановок,
размещений).
Формулы комбинаторики неудобны из-за
больших получаемых величин. В 1928 году
Хартли ввел двоичную логарифмическую
меру, позволяющую вычислять количество
информации в двоичных единицах – битах
[бит].
Количество информации по Хартли
определяется по формуле I = l × log2 h [бит],
где h – основание системы счисления
(количество состояний, которое может
принимать элемент, хранящий данное
число);
l – число элементов.
Бит по Хартли: количество разрядов равно 1,
основание – 2, log22 = 1 бит.
Бит является минимальной единицей
количества данных, которое может хранить
элемент с двумя устойчивыми состояниями
или передаваться по линии связи (есть
импульс – единица, нет импульса – ноль).
Были предложены и используются более
крупные единицы количества данных.
Байт (англ.) – единица измерения
количества информации, обычно равная
восьми битам. К сожалению, длина байта
строго не фиксиро- вана. Она может быть: 7
бит + 1 контрольный бит,
8 бит без контрольного бита,
8 бит + 1 контрольный бит.
37

38.

Статистическая мера информации
Требования к мере количества
информации
В каждом элементарном сообщении
содержится (для его получателя)
определенная информация – совокупность
сведений о состоянии дискретного источника
сообщений. Определяя количественную меру
этой информации, не будем учитывать ее
смысловое содержание. Очевидно, что при
отсутствии сведений о состоянии источника
имеется неопределенность относительно
того, какое сообщение xi из числа возможных
им выбрано, а при наличии этих сведений
данная неопределенность полностью
исчезает. Естественно количество
информации, содержащейся в дискретном
сообщении, измерять величиной
исчезнувшей неопределенности.
Рассмотрим основные подходы к оценке
количества информации в сообщении,
предварительно определив требования,
которым должна отвечать вводимая мера.
1. В общем случае чем больше число
возможных сообщений и, следовательно,
чем больше возможных значений сигнала,
тем больше априорная неопределенность и
тем большее количество информации
получает адресат, когда эта
неопределенность снимается. Иначе
говоря, количество информации должно
монотонно возрастать с увеличением
возможности выбора, т.е. объема алфавита
источника.
Если же выбор сообщения заранее
предопределен, то количество информации
в этом сообщении равно нулю.
38

39.

2. Вводимая мера должна обладать
свойством аддитивности, заключающимся в
следующем: если 2 независимых источника X и
Y с объемами алфавитов соответственно N и M
рассматривать как один источник,
одновременно реализующий пары состояний
xi и yj, то в соответствии с принципом
аддитивности полагают, что неопределенность
объединенного источника равна сумме
неопределенностей исходных источников.
Поскольку объем алфавита объединенного
источника XY равен N x M, то искомая
функция при равной вероятности состояний
источников должна удовлетворять условию
f(NxM) = f(N) + f(M).
Согласно основному логарифмическому тождеству:
Закон аддитивности информации:
Количество информации необходимое для установления пары
(х1, х2), равно сумме количеств информации необходимых
для независимого установления элементов х1 и х2.
Количество информации, содержащееся с одном символе,
называется его информационным весом и рассчитывается
по формуле Хартли
Мера неопределенности
(комбинаторный подход, мера Хартли)
Можно показать, что единственной
математической функцией, отвечающей
указанным требованиям, является
логарифмическая функция. Поэтому
перечисленные требования выполняются,
если в качестве меры неопределенности
источника с равновероятными состояниями
принять логарифм объема алфавита
источника.
Впервые такая оценка
неопределенности была введена в 1928 г. Р.
Хартли, предложившим степень
неопределенности опыта X с N различными
исходами характеризовать числом (с учетом
понятия энтропии, которое будет введено
позднее, эту характеристику можно назвать
энтропией источника с равновозможными
состояниями или максимально возможной
энтропией) H(X) = log N.
Согласно закону аддитивности, количество
информации, содержащееся в сообщении, состоящем
из m символов одного и того же алфавита, равно
39

40.

Основание логарифма не имеет
принципиального значения, и чаще всего в
качестве основания используется число 2.
При этом единица количества информации
называется двоичной единицей или битом и
представляет собой информацию,
содержащуюся в одном дискретном
сообщении источника равновероятных
сообщений с объемом алфавита равным,
двум. Для основания логарифма, равного 10,
единица количества информации
называется дит, а для натурального
логарифма – нат.
Легко видеть, что с ростом N величина H(X)
монотонно возрастает. В случае, если объем
алфавита источника равен 1 (т.е. когда
неопределенность отсутствует),
H(X)=0.
Однако ясно, что такая оценка
неопределенности учитывает не все
априорные сведения, характеризующие
опыт X. В этой оценке неопределенности
не учтены вероятности различных
исходов (поэтому такой подход
называется комбинаторным – все
вероятности равны).
Разумеется, Хартли понимал, что при
неодинаковых вероятностях генерации
различных сообщений такая оценка
становится малопоказательной, однако
он считал, что различия между
отдельными исходами определяются в
первую очередь психологическими
факторами и должны учитываться лишь
психологами, а не инженерами или
математиками.
Кроме того, величина H(X) обладает
свойством аддитивности.
40

41.

Вычисление количества информации для
равновероятных событий
Если события равновероятны, то количество
информации можно рассчитать по формуле:
N=2I,
где N – число возможных событий,
I – количество информации в битах.
Формула была предложена американским
инженером Р. Хартли в 1928 г.
Задача 1.
В коробке 32 карандаша, все карандаши
разного цвета. Наугад вытащили красный.
Какое количество информации при этом было
получено?
Решение.
Так как вытаскивание карандаша любого
цвета из имеющихся в коробке 32 карандашей
является равновероятным, то число
возможных событий равно 32.
N = 32, I = ? N = 2I , 32 = 25 , I = 5 бит.
Ответ: 5 бит
41

42.

42

43.

43

44.

Понятие об энтропии (вероятностный
подход, мера Шеннона)
Дальнейшее развитие понятие
неопределенности получило в работах К.
Шеннона. В общем случае, когда
вероятности различных состояний
источника неодинаковы, степень
неопределенности конкретного состояния
зависит не только от объема алфавита
источника, но и от вероятности этого
состояния. В такой ситуации количество
информации, содержащейся в одном
элементарном дискретном сообщении xk,
целесообразно определить как функцию
вероятности появления этого сообщения
p(xk) и характеризовать величиной