Измерение информации. Алфавитный подход к измерению информации

1. Измерение информации. Алфавитный подход к измерению информации

Уроки 5-6
Тема 2. ИНФОРМАЦИЯ
Измерение информации.
Алфавитный подход к
измерению информации
мощность алфавита;
информационный вес символа;
информационный объем текста;
единицы измерения информации;
скорость передачи информации.

2. Измерение информации.

Вопрос: «Как измерить информацию?»
Ответ на него зависит от того, что
понимать под информацией. Но
поскольку определять информацию
можно по-разному, то и способы
измерения тоже могут быть разными.
подробнее
Токмакова Людмила Викторовна, учитель информатики МБОУ «СОШ №32» ЭМР саратовской области

3. Алфавитный подход к измерению информации.

Алфавитный подход
к измерению информации.
Алфавитным подходом называется способ измерения информации,
который не связывает количество информации с содержанием
сообщения.
При алфавитном подходе к определению количества информации
отвлекаются от содержания информации и рассматривают
информационное сообщение как последовательность знаков
определенной знаковой системы.
Применение алфавитного подхода удобно прежде всего при
использовании технических средств работы с информацией. В этом
случае теряют смысл понятия «новые — старые», «понятные —
непонятные» сведения.
Алфавитный подход является объективным, т.е. он не зависит от
субъекта (человека), воспринимающего текст.
Проще всего разобраться в этом на примере текста, написанного на
каком-нибудь языке. Для нас удобнее, чтобы это был русский язык.

4. Алфавит, мощность алфавита

Все множество используемых в языке символов будем
традиционно называть алфавитом.
Обычно под алфавитом понимают только буквы, но поскольку
в тексте могут встречаться знаки препинания, цифры, скобки,
то мы их тоже включим в алфавит. В алфавит также следует
включить и пробел, т.е. пропуск между словами.
Полное количество символов алфавита принято называть
мощностью алфавита. Будем обозначать эту величину
буквой
N.
Например, мощность алфавита из заглавных русских букв и
отмеченных дополнительных символов равна 54 (буквы,
цифры, знаки препинания, пробел).
АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЬЪЭЮЯ0123456789().,!?
«»:-;(пробел)
Токмакова Людмила Викторовна, учитель информатики МБОУ «СОШ №32» ЭМР саратовской области

5. Информационный вес символа

Если допустить, что все символы алфавита встречаются в
тексте с одинаковой частотой (равновероятно), то
N=2i
где i – информационный вес одного символа в
используемом алфавите,
N – мощность алфавита.
Если весь текст состоит из К символов, то при
алфавитном подходе размер содержащейся в нем
информации равен:
I=К i
(информационный объем сообщения = количество символов в
сообщении * на вес одного символа)
Токмакова Людмила Викторовна, учитель информатики МБОУ «СОШ №32» ЭМР саратовской области

6. Сколько информации несет один символ в русском языке?

• Представьте себе, что текст к вам поступает последовательно,
по одному знаку, словно бумажная ленточка, выползающая из
телеграфного аппарата. Предположим, что каждый
появляющийся на ленте символ с одинаковой вероятностью
может быть любым символом алфавита.
• В каждой очередной позиции текста может появиться любой
из N символов.
• Тогда, согласно известной нам формуле 2i =N,
каждый
такой символ несет i бит информации, которое можно
определить из решения уравнения:
2i =54,
• В какую степень мы должны возвести 2, чтобы получить 54?
25=32, а 26=64. Мы можем подсчитать или посмотреть по
таблице степеней двойки и получаем: i = 5.755 бит.
• Вот сколько информации несет один символ в русском тексте!
Токмакова Людмила Викторовна, учитель информатики МБОУ «СОШ №32» ЭМР саратовской области

7. Количество информации в тексте. Задача1.

Для того, чтобы найти количество информации во всем
тексте, нужно посчитать число символов в нем и умножить на
«вес» одного символа - i.
Возьмём с книжной полки какую-нибудь книгу и посчитаем
количество информации на одной её странице.
Пусть страница содержит 50 строк.
В каждой строке — 60 символов.
Значит, на странице умещается 50x60=3000 знаков.
Тогда объем информации будет равен:
5,755 х 3000 = 17265 бит.
Следовательно, при алфавитном подходе к измерению
информации количество информации от содержания не
зависит. Количество информации зависит от объёма текста
(то есть от числа знаков в тексте) и от мощности алфавита.
Токмакова Людмила Викторовна, учитель информатики МБОУ «СОШ №32» ЭМР саратовской области

8. Количество информации в тексте.

Отсюда следует, например, что нельзя сравнивать
информационные объёмы текстов, написанных на разных
языках, только по объёму. У них отличаются информационные
веса одного символа так как мощности алфавитов разных
языков – различные.
Но если книги написаны на одном языке, то понятно, что в
толстой книге информации больше, чем в тонкой. При этом
содержательная сторона книги в расчёт не берётся.
Сформулируем правило, как измерить информацию,
используя для этого алфавитный подход.
Количество информации, содержащееся в
символьном сообщении, равно К х i,
где К – число символов в тексте сообщения,
а i – информационный вес символа,
который находится из уравнения 2i = N,
где N – мощность используемого алфавита
Токмакова Людмила Викторовна, учитель информатики МБОУ «СОШ №32» ЭМР саратовской области

9. Оформление решения задачи №1

ОБРАТИТЕ ВНИМАНИЕ!
Оформление решения задачи №1

10. Формула определения информационного веса символа двоичного алфавита

А что если алфавит состоит только из двух символов
0 и 1?
При использовании двоичной системы (алфавит
состоит из двух знаков: 0 и 1) каждый двоичный
знак несет 1 бит информации, так как в этом
случае: N = 2; N = 2i ; 2= 2i ; i = 1!
Интересно, что сама единица измерения
информации «бит» получила свое название от
английского сочетания «binary digit» - «двоичная
цифра».
Токмакова Людмила Викторовна, учитель информатики МБОУ «СОШ №32» ЭМР саратовской области

11. Достаточный алфавит

Удобнее всего измерять информацию, когда размер
алфавита N равен целой степени двойки. Например,
если N=16, то каждый символ несет 4 бита информации
потому, что
24 =16.
А если N=32, то один символ
«весит» 5 бит. 25 =32.
Ограничения
на
максимальный
размер
алфавита
теоретически не существует. Однако есть алфавит,
который можно назвать достаточным. С ним мы
встретимся при работе с компьютером. Это алфавит
мощностью 256 символов.
Токмакова Людмила Викторовна, учитель информатики МБОУ «СОШ №32» ЭМР саратовской области

12. Достаточный алфавит

В алфавит такого размера можно поместить все
практически
необходимые
символы:
латинские
и
русские буквы, цифры, знаки арифметических операций,
всевозможные скобки, знаки препинания.
Поскольку
28 =256,
то один символ этого алфавита
«весит» 8 бит. Причем 8 бит информации — это
настолько характерная величина, что ей даже присвоили
свое название — байт.
1 байт = 8 бит
Токмакова Людмила Викторовна, учитель информатики МБОУ «СОШ №32» ЭМР саратовской области

13. Достаточный алфавит. Количество информации в тексте.

Сегодня очень многие люди для подготовки писем, документов,
статей, книг и пр. используют компьютерные текстовые редакторы.
Компьютерные редакторы, в основном, работают с алфавитом
размером 256 символов. В этом случае легко подсчитать объем
информации в тексте.
Задача 2.
Если 1 символ алфавита несет 1 байт информации, то надо просто
сосчитать количество символов; полученное
число даст
информационный объем текста в байтах.
Пусть небольшая книжка, сделанная с помощью компьютера,
содержит 150 страниц; на каждой странице — 40 строк, в каждой
строке — 60 символов.
Значит страница содержит 40x60=2400 байт информации. Объем всей
информации в книге:
2400 х 150 = 360 000 байт.
Токмакова Людмила Викторовна, учитель информатики МБОУ «СОШ №32» ЭМР саратовской области

14. Оформление решения задачи №2

ОБРАТИТЕ ВНИМАНИЕ!
Оформление решения задачи №2

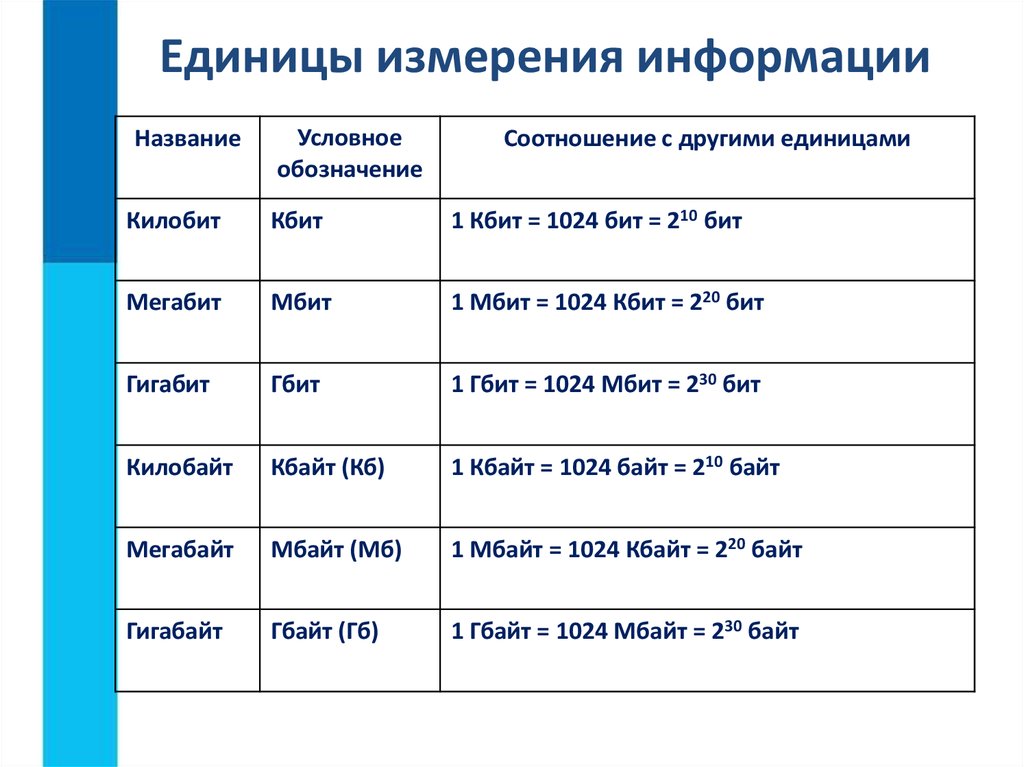
15. Единицы измерения информации

Название
Условное
обозначение
Соотношение с другими единицами
Килобит
Кбит
1 Кбит = 1024 бит = 210 бит
Мегабит
Мбит
1 Мбит = 1024 Кбит = 220 бит
Гигабит
Гбит
1 Гбит = 1024 Мбит = 230 бит
Килобайт
Кбайт (Кб)
1 Кбайт = 1024 байт = 210 байт
Мегабайт
Мбайт (Мб)
1 Мбайт = 1024 Кбайт = 220 байт
Гигабайт
Гбайт (Гб)
1 Гбайт = 1024 Мбайт = 230 байт

16. Задача 3.

Единицы измерения информации
Задача 3.
Сколько Кб составляет сообщение,
содержащее 8192 бит?
Решение:
1 байт = 8 бит;
1 Кбайт = 1024 байта;
8192 : 8 = 1024 байт = 1 Кб.
Ответ: 1 Кб.
Токмакова Людмила Викторовна, учитель информатики МБОУ «СОШ №32» ЭМР саратовской области

17. Оформление решения задачи №3

ОБРАТИТЕ ВНИМАНИЕ!
Оформление решения задачи №3

18. Задача 4.

Единицы измерения информации
Задача 4.
Сколько мегабайт информации
содержит сообщение объемом 223
бит? В ответе укажите одно число.
Решение.
223 бит = 210*210 *23 бит =
210*210 байт = 210 Кб = 1 Мб
Ответ: 1 Мб.
Токмакова Людмила Викторовна, учитель информатики МБОУ «СОШ №32» ЭМР саратовской области

19. Оформление решения задачи №4

ОБРАТИТЕ ВНИМАНИЕ!
Оформление решения задачи №4

20.

Скорость передачи информации.
Будем называть скоростью передачи информации
количество информации, выраженное в битах или
байтах, переданное в единицу времени. Скорость
передачи информации может измеряется в битах в
секунду - б/с, Килобитах в секунду - Кб/с или
Мегабитах в секунду - Мб/с. А также: в байтах в
секунду - Б/с, Килобайтах в секунду - КБ/с и т.д.,
соответственно.
(Замечу в скобках - многие мало знакомые с
информатикой люди часто путают б/с и Б/с (биты в
секунду с байтами в секунду), а они различаются в
8 раз!)
Токмакова Людмила Викторовна, учитель информатики МБОУ «СОШ №32» ЭМР саратовской области

21.

Скорость передачи информации.
Другое, очень схожее понятие, которое часто путают
со скоростью передачи информации - пропускная
способность канала. Измеряется она в тех же
единица, что и скорость, но если скорость передачи
информации показывает - как быстро передается
информация
от
источника
к
получателю
безотносительно к тому как и по каким каналам эта
информация
передается,
то
пропускная
способность канала показывает - как много
информации можно передать по конкретному
каналу передачи данных в единицу времени. Т.е.
пропускная способность - это максимально
возможная скорость передачи данных для
конкретного канала.
Токмакова Людмила Викторовна, учитель информатики МБОУ «СОШ №32» ЭМР саратовской области

22.

Скорость передачи информации.
При решении данных задачах необходимо найти
либо количество информации переданное через
интернет соединение, либо время этой самой
передачи, либо скорость передачи. Во всех случая
надо помнить, что есть связь между скоростью и
количеством информации
переданной в промежутке времени.
Токмакова Людмила Викторовна, учитель информатики МБОУ «СОШ №32» ЭМР саратовской области

23.

Скорость передачи информации.
Задача5.
Скорость передачи данных через ADSL-соединение равна
512000 бит/c. Передача файла через это соединение заняла
1 минуту. Определить размер файла в килобайтах.
Объем переданной информации Q вычисляется по формуле
Q=q*t , где q – пропускная способность канала (в битах в
секунду или подобных единицах), а t – время передачи.
Решение:
Выделим в заданных больших числах степени двойки;
переведем время в секунды (чтобы «согласовать» единицы
измерения), а скорость передачи – в Кбайты/с, поскольку ответ
нужно получить в Кбайтах:
t=1мин=60с=4*15с=22*15с
q=512000бит/c=512*1000бит/с=29 *125*8бит/с=29*53*23бит/с=
=212*53бит/с=29*53байт/с=53/2Кбайт/с
Токмакова Людмила Викторовна, учитель информатики МБОУ «СОШ №32» ЭМР саратовской области

24.

Скорость передачи информации.
Токмакова Людмила Викторовна, учитель информатики МБОУ «СОШ №32» ЭМР саратовской области

25. Оформление решения задачи №5

ОБРАТИТЕ ВНИМАНИЕ!
Оформление решения задачи №5

26. Закрепление:

Задача 6
Информационное сообщение объемом 0,125 Кб содержит 256
символов. Сколько символов содержит алфавит, при помощи которого
было записано это сообщение?
Решение:
Мощность алфавита (N) и информационный вес одного символа (i),
связаны между собой формулой:
2i =N
Объем информационного сообщения (I) и информационный вес
одного символа (i), связаны между собой формулой:
I =K*i
В битах объем сообщения составляет:
I=0,125 Кб * 1024 = 128 байт * 8 = 1024 бит.
Сообщение содержит 256 символов, следовательно,
i = 1024 : 256 = 4 бит (вес одного символа).
N = 24 = 16.
Ответ: алфавит содержит 16 символов.
Токмакова Людмила Викторовна, учитель информатики МБОУ «СОШ №32» ЭМР саратовской области

27. Закрепление:

Задача 7.
Сколько
школьных
учебников
емкостью
350
Кбайт
можно
разместить на трехдюймовой дискете,
если объем трехдюймовой дискеты –
1,44 Мбайт
Решение:
1Мбайт=1024Кбайт
1,44Мбайт = 1,44*1024 = 1474,56 Кбайт
1474,56 Кбайт / 350 Кбайт = 4 учебника
Токмакова Людмила Викторовна, учитель информатики МБОУ «СОШ №32» ЭМР саратовской области

28. Закрепление:

Задача 8.
Оцените информационный объем следующего
предложения:
Тяжело
в
ученье
–
легко
в
бою!
Так как каждый символ кодируется одним байтом,
нам только нужно подсчитать количество
символов, но при этом не забываем считать знаки
препинания и пробелы. Всего получаем 30
символов. А это означает, что информационный
объем данного сообщения составляет
30 байтов или 30 * 8 = 240 битов.
Токмакова Людмила Викторовна, учитель информатики МБОУ «СОШ №32» ЭМР саратовской области

29. Закрепление:

Задача 9.
Результатом одного измерения является целое
число от 0 до 100 процентов, которое
записывается
при
помощи
минимально
возможного количества бит. Станция сделала 80
измерений. Определите информационный объем
результатов наблюдений.
РЕШЕНИЕ:
От 0 до 100 - это 101 разное значение.
64<101<128, значит для кодирования надо 7
бит, 128=27.
7*80=560 бит. 560 бит = 560/8 = 70 байт.
ОТВЕТ: 70 байт
Токмакова Людмила Викторовна, учитель информатики МБОУ «СОШ №32» ЭМР саратовской области

30. Измерение информации. Содержательный подход к измерению информации

Уроки 5-6
Тема 2. ИНФОРМАЦИЯ
Измерение информации.
Содержательный подход к
измерению информации
мощность алфавита;
информационный вес символа;
информационный объем текста;
единицы измерения информации;
скорость передачи информации.

31. С позиции содержательного подхода к измерению информации решается вопрос о количестве информации в сообщении, получаемом

человеком. Рассматривается
следующая ситуация:

32. 1) человек получает сообщение о некотором событии; при этом заранее известна неопределенность знания человека об ожидаемом

событии. Неопределенность
знания может быть выражена либо числом возможных
вариантов события, либо вероятностью ожидаемых
вариантов события;
2) в результате получения сообщения
неопределенность знания снимается: из некоторого
возможного количества вариантов оказался выбранным
один;
3) по формуле вычисляется количество информации в
полученном сообщении, выраженное в битах.

33. Формула, используемая для вычисления количества информации, зависит от ситуаций, которых может быть две:

1. Все возможные варианты события
равновероятны. Их число конечно и равно
N.
2. Вероятности (p) возможных вариантов
события разные и они заранее известны:
{pi}, i = 1..N.
Здесь по-прежнему N — число возможных
вариантов события.

34. Равновероятные события

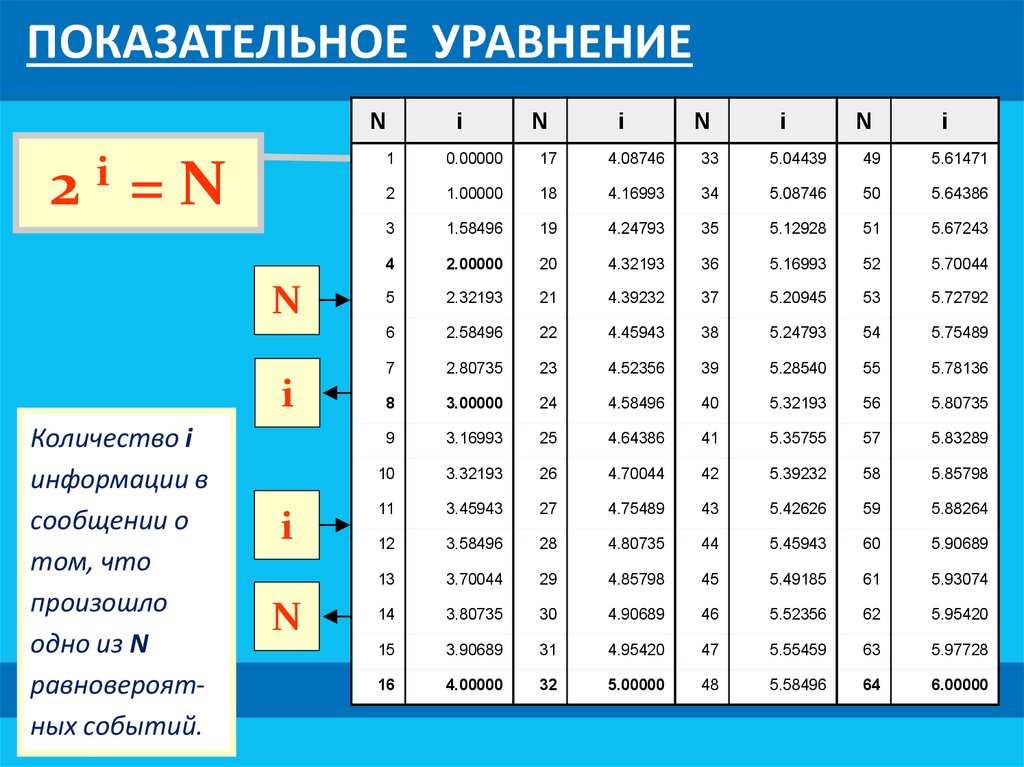
Если обозначить буквой i количество информации в
сообщении о том, что произошло одно из N
равновероятных событий, то величины i и N связаны
между собой формулой Хартли:
2i = N
1 бит — это количество информации в сообщении об одном из двух
равновероятных событий.
Формула Хартли — это показательное уравнение. Если i
— неизвестная величина, то решением данного
уравнения будет:
i = log2N
Данные формулы тождественны друг другу.

35.

ПОКАЗАТЕЛЬНОЕ УРАВНЕНИЕ
N
i
2 =N
N
i
Количество i
информации в
сообщении о
том, что
произошло
одно из N
равновероятных событий.
i
N
i
N
i
N
i
N
i
1
0.00000
17
4.08746
33
5.04439
49
5.61471
2
1.00000
18
4.16993
34
5.08746
50
5.64386
3
1.58496
19
4.24793
35
5.12928
51
5.67243
4
2.00000
20
4.32193
36
5.16993
52
5.70044
5
2.32193
21
4.39232
37
5.20945
53
5.72792
6
2.58496
22
4.45943
38
5.24793
54
5.75489
7
2.80735
23
4.52356
39
5.28540
55
5.78136
8
3.00000
24
4.58496
40
5.32193
56
5.80735
9
3.16993
25
4.64386
41
5.35755
57
5.83289
10
3.32193
26
4.70044
42
5.39232
58
5.85798
11
3.45943
27
4.75489
43
5.42626
59
5.88264
12
3.58496
28
4.80735
44
5.45943
60
5.90689
13
3.70044
29
4.85798
45
5.49185
61
5.93074
14
3.80735
30
4.90689
46
5.52356
62
5.95420
15
3.90689
31
4.95420
47
5.55459
63
5.97728
16
4.00000
32
5.00000
48
5.58496
64
6.00000

36. Рассмотрим несколько примеров:

Пример 1. Сколько информации содержит
сообщение о том, что из колоды карт
достали даму пик?
Решение: В колоде 32 карты. В
перемешанной колоде выпадение
любой карты — равновероятные
события. Если i — количество
информации в сообщении о том, что
выпала конкретная карта (например,
дама пик), то из уравнения Хартли:
2i = 32 =
25
Отсюда: i = 5 бит.

37.

Пример 2. Сколько информации содержит
сообщение о выпадении грани с числом 3 на
шестигранном игральном кубике?
Решение: Считая выпадение
любой грани событием
равновероятным, запишем
формулу Хартли:
2i = 6.
Отсюда: i = log26 = 2,58496 бит.

38. Неравновероятные события (вероятностный подход). Если вероятность некоторого события равна p, а i (бит) — это количество

информации в сообщении о том, что произошло это
событие, то данные величины связаны между собой
формулой:
2i = 1/p
Решая данное показательное уравнение
относительно i, получаем:
i = log2(1/p)
формула Шеннона

39. Качественный подход

• Информация — это знания людей,
получаемые ими из различных сообщений.
• Сообщение — это информационный поток
(поток данных), который в процессе передачи
информации поступает к принимающему его
субъекту.
Сообщение
Информативные сообщение,
которое пополняет знания
человека, т.е. несет для
него информацию.
Неинформативные сведения
“старые”, т.е. человек это
уже знает, или содержание
сообщения непонятно
человеку

40. Количественный подход в приближении равновероятности

События равновероятны, если ни одно из них не
имеет преимущества перед другими.
Рассмотрим на примере.
«Сколько информации несет сообщение о результате
бросания шестигранного кубика?»
Из уравнения Хартли: 2i = 6.
Поскольку 22 < 6 < 23, следовательно, 2 < i < 3.
Затем определяем более точное значение (с точностью до
пяти знаков после запятой), что i = 2,58496 бит.
Отметить, что при данном подходе количество информации
может быть выражено дробной величиной.

41. Вероятностный подход к измерению информации

Вероятность некоторого события — это величина,
которая может принимать значения от нуля до единицы.
Вероятность невозможного события равна нулю
(например: «завтра Солнце не взойдет над горизонтом»)
Вероятность достоверного события равна единице
(например: «Завтра солнце взойдет над горизонтом»).
Вероятность некоторого события определяется путем
многократных наблюдений (измерений, испытаний). Такие
измерения называют статистическими. И чем большее
количество измерений выполнено, тем точнее
определяется вероятность события.

42. Рассмотрим несколько примеров:

Пример 3. На автобусной
остановке останавливаются два
маршрута автобусов: № 5 и № 7.
Ученику дано задание: определить,
сколько информации содержит
сообщение о том, что к остановке
подошел автобус № 5, и сколько
информации в сообщении о том, что
подошел автобус № 7.

43.

Решение: Ученик провел исследование. В течение
всего рабочего дня он подсчитал, что к остановке
автобусы подходили 100 раз.
Из них — 25 раз подходил автобус № 5 и 75 раз
подходил автобус № 7.
Сделав предположение, что с такой же частотой
автобусы ходят и в другие дни, ученик вычислил
вероятность появления на остановке автобуса № 5:
p5 = 25/100 = 1/4,
и вероятность появления автобуса № 7:
p7 = 75/100 = 3/4.
Отсюда, количество информации в сообщении об
автобусе № 5 равно:
i5 = log24 = 2 бита.
Количество информации в сообщении об автобусе
№ 7 равно:
i7 = log2(4/3) = log24 – log23 = 2 – 1,58496 = 0,41504
бита.

44.

Пример 4. Рассмотрим другой вариант задачи об
автобусах. На остановке останавливаются автобусы № 5 и
№ 7. Сообщение о том, что к остановке подошел автобус №
5, несет 4 бита информации. Вероятность появления на
остановке автобуса с № 7 в два раза меньше, чем
вероятность появления автобуса № 5. Сколько бит
информации несет сообщение о появлении на остановке
автобуса № 7?
Решение: Запишем условие задачи в следующем
виде:
i5 = 4 бита, p5 = 2 · p7
Вспомним связь между вероятностью и количеством
информации: 2i = 1/p
Отсюда: p = 2–i
Подставляя в равенство из условия задачи, получим:
Отсюда:

45.

Из полученного результата следует
вывод: уменьшение вероятности
события в 2 раза увеличивает
информативность сообщения о нем на
1 бит.
Очевидно и обратное правило:
увеличение вероятности события в 2
раза уменьшает информативность
сообщения о нем на 1 бит. Зная эти
правила, предыдущую задачу можно
было решить «в уме».

46.

Методические рекомендации по
решению задач:
Если мощность алфавита неизвестна, то единицы
измерения
информации
должны
быть
переведены в биты, только при использовании
достаточного алфавита, единицы измерения –
байты.
В условиях задач по обсуждаемой теме
связываются
между
собой
следующие
величины: мощность символьного алфавита —
N; информационный вес символа — i; число
символов в тексте (объем текста) — К;
количество информации, заключенное в тексте
(информационный объем текста) — I. Кроме
того, при решении задач требуется знать связь
между различными единицами информации:
бит, байт, Кбайт, Мбайт.