Similar presentations:
Иррациональные неравенства
1.
2.
Разложим второе подкоренное выражение на множителиТогда уравнение примет вид
3.
1 случай.2 случай
тогда x=a – корень уравнения
тогда обе части уравнения можно
разделить на это выражение,
не забывая при этом, что подкоренное
выражение неотрицательное.
4.
Учитывая, что, то
Итак, если
Если
, то
, получаем
- корень уравнения;
x=a – корень уравнения
Таким образом, при a<0 уравнение имеет один корень
при
уравнение имеет два корня x=a и
При
корни совпадают ( один корень)
При
уравнение имеет один корень x=a
Ответ:
5. Вы умеете решать неравенства? Уверены?
.Вы умеете решать неравенства?
Уверены?
Чего нельзя делать при решении неравенств?
Вот 7 ловушек, в которые часто попадают абитуриенты.
1. Нельзя умножать (или делить) неравенство на
выражение, знака которого нам неизвестен.
2. Извлекать из неравенства корень четной степени
тоже нельзя. Такого действия просто нет.
3. Как решать неравенство
> 0?
4. Возводить обе части неравенства в квадрат можно только если
они неотрицательны
6. Вы умеете решать неравенства? Уверены?
.Вы умеете решать неравенства?
Уверены?
5. Помним о том, в каких случаях знак показательного или
логарифмического неравенства меняется,
а в каких – остается тем же.
«Отбрасывая» логарифмы, делаем это грамотно.
6. Если в неравенстве есть дроби, корни четной степени или
логарифмы – там обязательно будет ОДЗобласть допустимых значений.
7. Сложная тем для старшеклассников – задачи с
модулем. Проверьте, умеете ли вы их решать
7. БАЗОВЫЕ ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА
• Практически все сложныеиррациональные неравенства, в конечном
итоге сводятся к базовым иррациональным
неравенствам трех типов.
f ( x) g ( x)
f ( x) g ( x)
f ( x)
g ( x)
8. РЕШЕНИЕ НЕРАВЕНСТВ 1 ТИПА
9. РЕШЕНИЕ НЕРАВЕНСТВ 2 ТИПА
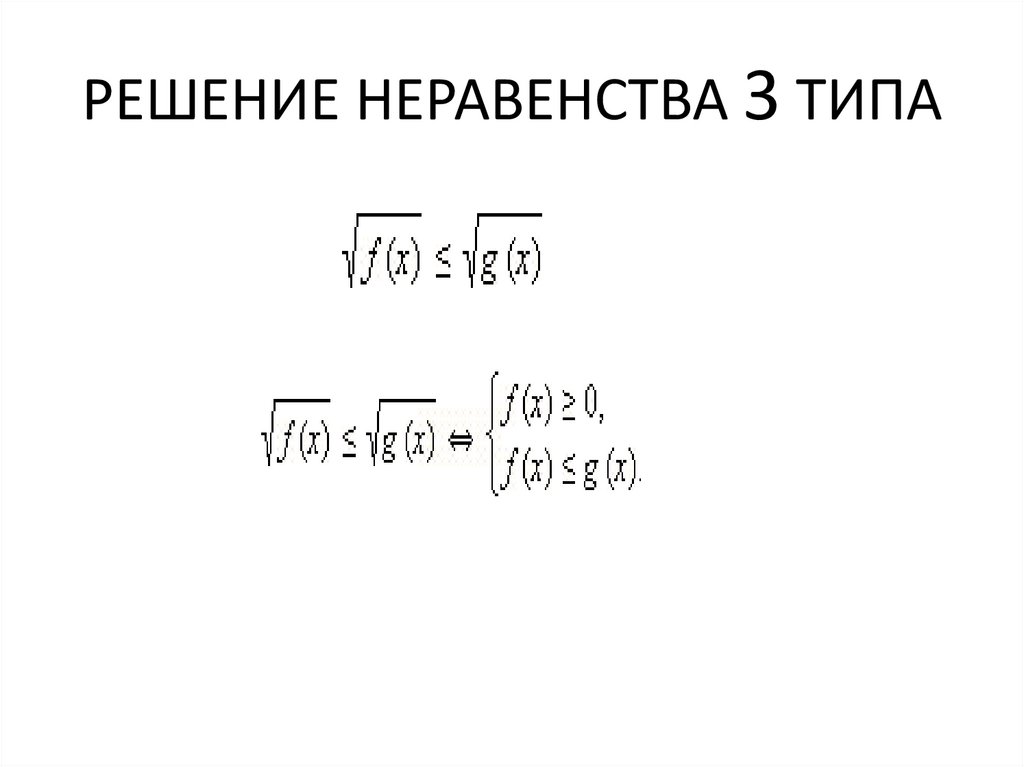
10. РЕШЕНИЕ НЕРАВЕНСТВА 3 ТИПА
11. Иррациональные неравенства
1.2.
3.
4.
5.
6.
7.
12. Иррациональные неравенства
8.9.
10.
11.
12.
13.
< -1
13. Пробный экзамен, вариант 202
Пусть, тогда
или












 mathematics
mathematics








